Volume 2013, Issue 1 694043

Research Article

Open Access

On Solution of Fredholm Integrodifferential Equations Using Composite Chebyshev Finite Difference Method

Z. Pashazadeh Atabakan,

Z. Pashazadeh Atabakan

Department of Mathematics, Universiti Putra Malaysia (UPM), 43400 Serdang, Selangor, Malaysia upm.edu.my

Search for more papers by this author

A. Kazemi Nasab,

A. Kazemi Nasab

Department of Mathematics, Universiti Putra Malaysia (UPM), 43400 Serdang, Selangor, Malaysia upm.edu.my

Search for more papers by this author

A. Kılıçman,

Corresponding Author

A. Kılıçman

[email protected]

Department of Mathematics, Universiti Putra Malaysia (UPM), 43400 Serdang, Selangor, Malaysia upm.edu.my

Search for more papers by this author

Z. Pashazadeh Atabakan,

Z. Pashazadeh Atabakan

Department of Mathematics, Universiti Putra Malaysia (UPM), 43400 Serdang, Selangor, Malaysia upm.edu.my

Search for more papers by this author

A. Kazemi Nasab,

A. Kazemi Nasab

Department of Mathematics, Universiti Putra Malaysia (UPM), 43400 Serdang, Selangor, Malaysia upm.edu.my

Search for more papers by this author

A. Kılıçman,

Corresponding Author

A. Kılıçman

[email protected]

Department of Mathematics, Universiti Putra Malaysia (UPM), 43400 Serdang, Selangor, Malaysia upm.edu.my

Search for more papers by this author

First published: 11 June 2013

https://doi.org/10.1155/2013/694043

Citations: 7

Academic Editor: Mustafa Bayram

Share a link

Email
Wechat
Bluesky

Abstract

A new numerical method is introduced for solving linear Fredholm integrodifferential equations which is based on a hybrid of block-pulse functions and Chebyshev polynomials using the well-known Chebyshev-Gauss-Lobatto collocation points. Composite Chebyshev finite difference method is indeed an extension of the Chebyshev finite difference method and can be considered as a nonuniform finite difference scheme. The main advantage of the proposed method is reducing the given problem to a set of algebraic equations. Some examples are given to approve the efficiency and the accuracy of the proposed method.

1. Introduction

Linear and nonlinear Fredholm integrodifferential equations can be used to model many problems of science and theoretical physics such as engineering, biological models, electrostatics, control theory of industrial mathematics, economics, fluid dynamics, heat and mass transfer, oscillation theory, and queuing theory [1].

In recent years, many authors have considered different numerical methods to solve these kinds of problems. In 2012, Dehghan and Salehi employed [2] the meshless moving least square method for solving nonlinear Fredholm integrodifferential equations. A sequential method for the solution of Fredholm integrodifferential equations was presented by Berenguer et al. [3] in 2012. The formulation of the Fredholm integrodifferential equation in terms of an operator and the use of Schauder bases are the main tools of this method.

In [4], the operational Adomian-Tau method with Pade approximation was used for solving nonlinear Fredholm integrodifferential equations. This approach is based on two matrices, and Pade approximation was used to improve the accuracy of the method. Chebyshev finite difference method was proposed in [5] in order to solve Fredholm integrodifferential equations. In this scheme the problem is reduced to a set of algebraic equations. In [6], Legendre collocation matrix method was introduced for solving high-order linear Fredholm integrodifferential equations. In this way, the equation and its conditions are converted to matrix equations using collocation points on the interval [−1,1]. Atabakan et al. [7, 8] proposed a modification of homotopy analysis method (HAM) known as spectral homotopy analysis method (SHAM) to solve linear Volterra and Fredholm integrodifferential equations. In this procedure, the Chebyshev pseudospectral method was used to obtain an approximation of solutions to higher-order equation. The semiorthogonal spline method was discussed in [9]. This approach is used to solve Fredholm integral and integrodifferential equations.

In this paper, we applied a composite Chebyshev finite difference (ChFD) method for solving Fredholm integrodifferential equations. Fredholm integro differential equation is given by

(1)

where k(x, t), f(x), and y(x) are analytic functions, λ is a constant value, G_r, r = 0, …, n − 1, are linear functions and the points τ₀, τ₁, …, τ_n lie in [0, T]. It will always be assumed that (1) possesses a unique solution y ∈ Cⁿ[0, T].

The base of the proposed method is a hybrid of block-pulse functions and Chebyshev polynomials using Chebyshev-Gauss-Lobatto points. This method was introduced and applied for solving the optimal control of delay systems with a quadratic performance index in [10, 11].

Chebyshev polynomials which are the eigenfunctions of a singular Sturm-Liouville problem have many advantages. They can be considered as a good representation of smooth functions by finite Chebyshev expansions provided that the function is infinitely differentiable. The Chebyshev expansion coefficients converge faster than any finite power of 1/m as m goes to infinity for problems with smooth solutions. The numerical differentiation and integration can be performed. Moreover, they have been applied to solve different kinds of boundary value problems [12–14].

The paper is organized in the following way. Section 2 includes some necessary preliminaries and notations. Chebyshev finite difference method and composite Chebyshev finite difference method for solving Fredholm integrodifferential equations are described in Sections 3 and 4, respectively. Convergence analysis of the proposed method is presented in Section 5. In Section 6 discretization of the method is introduced, and some numerical examples are presented in Section 7. In Section 8, concluding remarks are given.

2. Preliminaries and Notations

In this section, we present some notations, definitions, and preliminary facts that will be used further in this work.

2.1. Block-Pulse Functions (BPF)

In order to introduce block-pulse functions, we first suppose the interval [0, T) to be divided into K equidistant subintervals [((k − 1)/K)T, (k/K)T), k = 1,2, …, K. A set of block-pulse functions B_(K)(t) composed of K orthogonal functions with piecewise constant values is defined on the semiopen interval [0, T) as follows:

(2)

where the kth component is given by

(3)

Block-pulse functions have some nice characteristics. They are disjoint and orthogonal; that is,

(4)

where δ_k,l is the Kronecker delta function. In addition, the set of block-pulse functionies satisfy Parseval’s identity when K tends to infinity. In other words, for any function v ∈ £²[0, T),

(5)

where

(6)

so they are complete. For more information about block-pulse functions, interested reader is referred to [20–30].

2.2. Chebyshev Polynomials

Chebyshev polynomials of the first kind of degree m can be defined as follows [12]:

(7)

which are orthogonal with respect to the weight function

, where

(8)

Chebyshev polynomials also satisfy the following recursive formula:

(9)

The set of Chebyshev polynomials is a complete orthogonal set in the Hilbert space

. The Chebyshev expansion of a function

(10)

where

(11)

They have also another useful characteristic; see [14]. If

(12)

then

(13)

2.3. Hybrid Functions of Block-Pulse and Chebyshev Polynomials

The orthogonal set of hybrid functions b_km(t), k = 1,2, …, K, m = 0,1, …M, is defined on the interval [0, T) as

(14)

where k and m are the order of block-pulse functions and Chebyshev polynomials, respectively. The set of hybrid functions of block-pulse and Chebyshev polynomials is a complete orthogonal set in the Hilbert space

because the set of block-pulse functions and the set of Chebyshev polynomials are completely orthogonal. In view of the following formula:

(15)

in which δ_kp is the Kronecker delta function and w_k(t), k = 1,2, …, K, are the corresponding weight functions on the kth subinterval [((k − 1)/K)T, (k/K)T) and defined as

(16)

we can conclude that the hybrid functions are orthogonal with respect to weight functions w_k. The set of hybrid functions is complete, so any function

can be written as follows:

(17)

in which

(18)

where (·, ·) w_k is the weighted inner product.

3. Chebyshev Finite Difference Method

We can approximate a function f(t) in terms of Chebyshev polynomials as follows [31]:

(19)

with double primes meaning that the first and last terms should be halved. Moreover, t_k are the extrema of the Mth-order Chebyshev polynomial T_M(t) and defined as

(20)

In view of (7), we have

(21)

so f_m can be rewritten as

(22)

The first three derivatives of the function f(t) at the points t_m, m = 0,1, …, M, are given in [32, 33] as

(23)

where

(24)

(25)

with θ₀ = θ_M = 1/2, θ_j = 1 for j = 1,2, …M − 1.

As can be seen from (23), the first three derivatives of the function f(t) at any point of the Chebyshev-Gauss-Lobatto points is expanded as a linear combination of the values of the function at these points.

In view of (13) and (19), we have

(26)

4. Composite Chebyshev Finite Difference Method

In this Section, we present the composite Chebyshev finite difference (ChFD) method. Consider t_km, k = 1,2, …, K, m = 0,1, …, M, as the corresponding Chebyshev-Gauss-Lobatto collocation points at the kth subinterval [(k − 1)/K, k/K] such that

(27)

A function f(t) can be written in terms of hybrid basis functions as follows:

(28)

where f_km, n = 1,2, …, K, m = 0,1, …, M, are the expansion coefficients of the function f(t) at the subinterval [(k − 1)/K, k/K] and b_k,m(t), k = 1,2, …, K, m = 0,1, …, M, are defined in (14).

In view of (14) and (19), we can obtain the coefficients f_km as

(29)

Using (23)–(25), the first three derivatives of the function f(t) at the points t_km, k = 1,2, …, K, m = 0,1, …, M, can be obtained as

(30)

where

(31)

In view of (26) and (28), we get

(32)

5. Convergence Analysis

A detailed proof of the following results can be found in [11].

Lemma 1. If the hybrid expansion of a continuous function h(t) converges uniformly, then it converges to the function h(t).

Theorem 2. A function with bounded second derivative, say |h^′′(t)| ≤ B, can be expanded as an infinite sum of hybrid functions and the series converges uniformly to h(t), that is,

(33)

Theorem 3. Suppose that with bounded second derivative, say |h^′′(t)| ≤ B, and then its hybrid expansion converges uniformly to h(t); that is,

(34)

where the summation symbol with prime denotes a sum with the first term halved.

Theorem 4 (accuracy estimation). Suppose that with bounded second derivative, say |h^′′(t)| ≤ B, and then one has the following accuracy estimation:

(35)

where

(36)

Proof. Consider

(37)

With the aid of (15) and the proof of Theorem 3, we will have

(38)

where

(39)

6. Discretization of Problem

In this section, we apply the composite ChFD method to solve Fredholm integrodifferential equations of the form (1). For this purpose, we approximate integral part in (1) using (32). We expand k(x, t)y(t) in terms of hybrid functions:

(40)

where

(41)

with aid of (32), we will have

(42)

In order to obtain the solution y(x) in (1), by applying the composite ChFD method, we first collocate (1) in Chebyshev-Gauss-Lobatto collocation points t_km, k = 1, …, K, m = 0,1, …, M − n. In addition, substituting (28) and (30) into boundary conditions (1), we get n equations. Moreover, the approximate solution and its first n derivatives should be continuous at the interface of subintervals; that is,

(43)

Therefore, we have a system of K(M + 1) algebraic equations, which can be solved by using Newton′s iterative method for the unknowns y(t_km), k = 0,1, …, K, m = 0,1, …, M. Consequently, the approximate solution y(x) of (1) can be calculated.

7. Numerical Examples

In this section, we apply the technique described in Section 6 to some illustrative examples of higher-order linear Fredholm integrodifferential equations.

Example 1. Consider the second-order Fredholm integrodifferential equation [5, 15]

(44)

subject to the boundary conditions

(45)

with the exact solution y(x) = 1/(x² + 1).

We solve the problem with M = 10, and K = 8. A comparison between absolute errors in solutions obtained by composite Chebyshev finite difference method, wavelet collocation method, wavelet Galerkin and Chebyshev finite difference method is tabulated in Table 1. As can been seen in Table 1, our results are much more accurate than those K obtained by other methods specially wavelet collocation method.

Table 1. A comparison of absolute errors between Wc, WG, Cfd, and present method.

x	Wavelet collocation [15]	Wavelet Galerkin [15]	Chebyshev finite difference [5]	Present method
0.125	9.3 × 10⁻⁴	7.9 × 10⁻⁷	2.1 × 10⁻⁹	1.16 × 10⁻¹⁵
0.250	1.6 × 10⁻³	1.3 × 10⁻⁶	2.0 × 10⁻⁸	2.28 × 10⁻¹⁵
0.375	2.0 × 10⁻³	1.6 × 10⁻⁶	1.8 × 10⁻⁷	1.27 × 10⁻¹⁵
0.500	1.9 × 10⁻³	1.6 × 10⁻⁶	1.9 × 10⁻⁸	3.15 × 10⁻¹⁶
0.625	1.6 × 10⁻³	1.5 × 10⁻⁶	1.9 × 10⁻⁷	2.79 × 10⁻¹⁷
0.750	1.1 × 10⁻³	1.1 × 10⁻⁶	4.9 × 10⁻⁸	1.63 × 10⁻¹⁶
0.875	5.5 × 10⁻⁴	6.5 × 10⁻⁷	4.2 × 10⁻⁸	1.52 × 10⁻¹⁵

The maximum errors for approximate solution y_KM(x) can be defined as

(46)

where the computed result with K is shown by y_KM and y_exact(x) is the exact solution. For different values of K, the errors of E_KM are presented in Table 2.

Table 2. The maximum errors of E_KM for different values of K and M.

K	4	10	8
M	8	8	10
E_KM	6.66 × 10⁻¹⁰	3.01 × 10⁻¹³	2.28 × 10⁻¹⁵

Example 2. Consider the second-order Fredholm integrodifferential equation [5, 15]

(47)

subject to the boundary condition

(48)

The exact solution of this equation is y(x) = e^x.

The problem is solved with M = 7, and K = 8. A comparison between absolute errors in solutions by composite Chebyshev finite difference method, wavelet collocation method, wavelet Galerkin and Chebyshev finite difference method is tabulated in Table 3. It is clear from Table 3 that our method is reliable and applicable to handle Fredholm integrodifferential equations. For different values of K, the errors of E_KM are shown in Table 4.

Table 3. A comparison of absolute errors between Wc, WG, Cfd, and present method.

x	Wavelet collocation [15]	Wavelet Galerkin [15]	Chebyshev finite difference [5]	Present method
0.125	2.6 × 10⁻²	2.7 × 10⁻⁴	1.8 × 10⁻¹⁰	1.45 × 10⁻¹⁵
0.250	1.5 × 10⁻²	3.0 × 10⁻⁵	4.4 × 10⁻¹⁰	1.78 × 10⁻¹⁵
0.375	9.3 × 10⁻³	2.6 × 10⁻⁴	1.4 × 10⁻⁹	1.71 × 10⁻¹⁵
0.500	5.1 × 10⁻³	4.3 × 10⁻⁴	2.4 × 10⁻¹⁰	5.00 × 10⁻¹⁵
0.625	2.5 × 10⁻³	5.6 × 10⁻⁴	1.7 × 10⁻⁹	1.22 × 10⁻¹⁵
0.750	1.0 × 10⁻³	6.5 × 10⁻⁴	7.7 × 10⁻¹⁰	8.66 × 10⁻¹⁶
0.875	2.3 × 10⁻⁴	7.2 × 10⁻⁴	1.3 × 10⁻⁹	4.52 × 10⁻¹⁶

Table 4. The maximum errors of E_KM for different values of K and M.

K	8	10	8
M	6	6	7
E_KM	6.01 × 10⁻¹³	8.72 × 10⁻¹⁴	1.22 × 10⁻¹⁵

Example 3. Consider the second-order Fredholm integrodifferential equation [5, 16]

(49)

subject to

(50)

with the exact solution y(x) = e^x.

In order to apply the presented method for solving the given problem, we should transform using an appropriate change of variables as

(51)

In this example, we set M = 9, and K = 10. In Table 5, absolute errors in solutions obtained by composite Chebyshev finite difference method are compared with Tau method and Chebyshev finite difference method. According to Table 5 using the proposed method, we can obtain approximate solution which is almost same as exact solution. For different values of K the errors of E_KM are shown in Table 6.

Table 5. A comparison of absolute errors between Tm, Cfm, and present method.

x	Exact solution	Tau method [16]	Chebyshev finite difference [5]	Present method
−1.0	0.367879441	1.52 × 10⁻⁶	1.19 × 10⁻⁸	1.32 × 10⁻¹⁶
−0.8	0.449328964	1.74 × 10⁻⁶	1.33 × 10⁻⁸	1.36 × 10⁻¹⁶
−0.6	0.548811636	1.95 × 10⁻⁶	1.29 × 10⁻⁸	1.38 × 10⁻¹⁶
−0.4	0.670320046	2.02 × 10⁻⁶	1.43 × 10⁻⁸	1.40 × 10⁻¹⁶
0.2	0.818730753	1.97 × 10⁻⁶	1.27 × 10⁻⁸	1.20 × 10⁻¹⁶
0.0	1.000000000	1.83 × 10⁻⁶	1.02 × 10⁻⁸	9.99 × 10⁻¹⁶
0.2	1.221402758	1.63 × 10⁻⁶	1.04 × 10⁻⁸	7.91 × 10⁻¹⁷
0.4	1.491824698	1.36 × 10⁻⁶	8.68 × 10⁻⁹	7.31 × 10⁻¹⁷
0.6	1.822118800	1.04 × 10⁻⁶	2.92 × 10⁻⁹	3.08 × 10⁻¹⁷
0.8	2.225540928	5.56 × 10⁻⁷	1.65 × 10⁻⁹	3.69 × 10⁻¹⁷
1.0	2.718281828	1.52 × 10⁻⁶	1.19 × 10⁻⁸	1.32 × 10⁻¹⁶

Table 6. The maximum errors of E_KM for different values of K and M.

K	4	10	8
M	8	8	10
E_KM	4.07 × 10⁻¹²	3.93 × 10⁻¹⁵	2.79 × 10⁻¹⁷

Example 4. Consider the first-order Fredholm integrodifferential equation [3, 17–19]

(52)

subject to

(53)

M = 9, and K = 4 are considered to solve Example 4. In Table 7, absolute errors in solutions obtained by composite Chebyshev finite difference method are compared with CAS wavelet method, differential transfer method, Improved homotopy perturbation method, and a sequential method. It is illustrated in Table 7 that the results obtained using current method are very closed to exact solution. The graph of absolute errors for M = 9, and K = 4 is shown in Figure 1.

Table 7. A comparison of absolute errors between DTM, IHPM, Sa, and present method.

x	CAS wavelet method [17]	DT method [18]	Improved homotopy perturbation [19]	Sequential approach [3]	Present method
0.1	1.34 × 10⁻³	1.00 × 10⁻²	0.23 × 10⁻⁵	1.01 × 10⁻⁷	1.25 × 10⁻¹⁷
0.2	1.15 × 10⁻³	2.78 × 10⁻²	0.92 × 10⁻⁵	4.82 × 10⁻⁷	4.27 × 10⁻¹⁷
0.3	5.67 × 10⁻³	5.08 × 10⁻²	0.20 × 10⁻⁴	1.017 × 10⁻⁶	1.46 × 10⁻¹⁶
0.4	5.93 × 10⁻²	7.08 × 10⁻²	0.37 × 10⁻⁴	1.61 × 10⁻⁶	1.53 × 10⁻¹⁶
0.5	1.32 × 10⁻²	9.71 × 10⁻²	0.57 × 10⁻⁴	2.30 × 10⁻⁶	1.44 × 10⁻¹⁶
0.6	4.39 × 10⁻²	1.09 × 10⁻¹	0.83 × 10⁻⁴	3.09 × 10⁻⁶	1.68 × 10⁻¹⁶
0.7	1.41 × 10⁻²	1.04 × 10⁻¹	0.11 × 10⁻³	3.97 × 10⁻⁶	1.74 × 10⁻¹⁶
0.8	1.34 × 10⁻²	6.94 × 10⁻²	0.14 × 10⁻³	4.90 × 10⁻⁶	5.40 × 10⁻¹⁷
0.9	1.32 × 10⁻²	1.00 × 10⁻²	0.18 × 10⁻³	6.13 × 10⁻⁶	1.72 × 10⁻¹⁷

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The graph of absolute errors for Example 4 for K = 4, and M = 9.

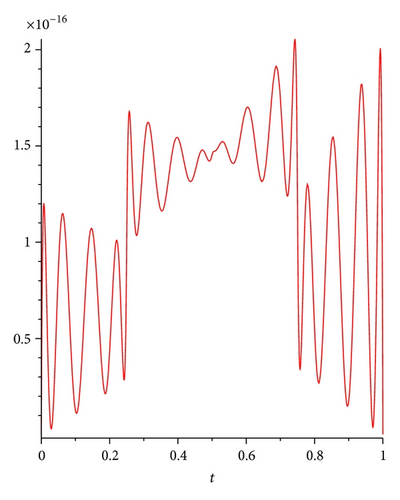
Example 5. Consider the first-order Fredholm integrodifferential equation [6, 34, 35]

(54)

subject to

(55)

This example is solved for M = 8 and K = 4. In order to apply the presented method for solving the given problem, we should transform using an appropriate change of variables as

(56)

In Table 8, absolute errors in solutions obtained by composite Chebyshev finite difference method are compared with Legendre polynomial method. As can be shown in Table 8, the introduced method is more efficient than Legendre polynomial method, and the numerical results are in good agreement with exact solutions up to 13 decimal places. The graph of absolute errors for K = 4, and M = 8 is shown in Figure 2.

Table 8. A comparison of absolute errors between Lps and ChFd.

x	Legendre polynomial solutions [6]	Present method
−1.0	1.00 × 10⁻⁸	0
−0.8	1.00 × 10⁻⁸	2.98 × 10⁻¹³
−0.6	0.00	6.56 × 10⁻¹³
−0.4	1.00 × 10⁻⁸	9.80 × 10⁻¹³
−0.2	0.00	1.13 × 10⁻¹³
0.0	0.00	1.18 × 10⁻¹²
0.2	1.00 × 10⁻⁸	9.18 × 10⁻¹²
0.4	0.00	8.34 × 10⁻¹³
0.6	2.00 × 10⁻⁸	7.80 × 10⁻¹³
0.8	4.60 × 10⁻⁷	4.75 × 10⁻¹³
1.0	5.25 × 10⁻⁶	0

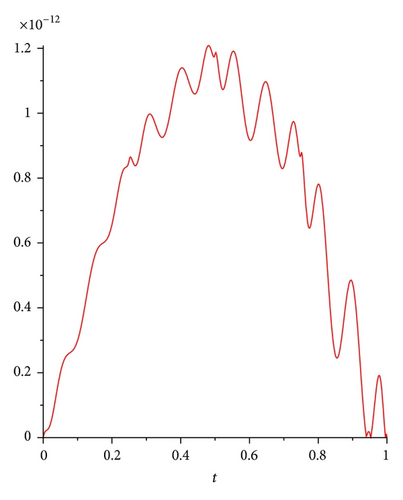
Example 6. Consider the third-order linear Fredholm integrodifferential equation [6]

(57)

subject to

(58)

The exact solution for this problem is y(x) = sinx. We solve the problem with m = 9, and n = 10. In Table 9, absolute errors in solutions obtained by composite Chebyshev finite difference method are compared with Legendre polynomial solutions. For different values of K the errors of E_KM are shown in Table 10. The graph of absolute errors for K = 10, and M = 9 is shown in Figure 3.

Table 9. A comparison of absolute errors between Lps and present method.

x	Exact solution	Legendre polynomial solutions [6]	Present method
−1.0	−0.8414709848	4.39 × 10⁻⁹	7.00 × 10⁻²⁰
−0.8	−0.7173560909	4.69 × 10⁻⁹	1.50 × 10⁻¹⁵
−0.6	−0.5646424734	1.19 × 10⁻⁹	4.91 × 10⁻¹⁵
−0.4	−0.3894183423	2.30 × 10⁻⁹	8.38 × 10⁻¹⁵
−0.2	−0.1986693308	9.50 × 10⁻¹¹	1.05 × 10⁻¹⁴
0.0	0.0	1.99 × 10⁻¹⁷	1.07 × 10⁻¹⁴
0.2	0.1986693308	1.04 × 10⁻¹⁰	8.79 × 10⁻¹⁵
0.4	0.3894183423	1.06 × 10⁻⁸	5.34 × 10⁻¹⁵
0.6	0.5646424734	5.00 × 10⁻⁸	1.48 × 10⁻¹⁵
0.8	0.7173560909	1.35 × 10⁻⁶	1.11 × 10⁻¹⁵
1.0	0.8414709848	4.65 × 10⁻⁷	7.00 × 10⁻²⁰

Table 10. The maximum errors of E_KM for different values of K and M.

K	4	5	9	10
M	5	5	8	9
E_KM	4.13 × 10⁻⁶	3.32 × 10⁻⁶	3.77 × 10⁻¹⁴	1.07 × 10⁻¹⁴

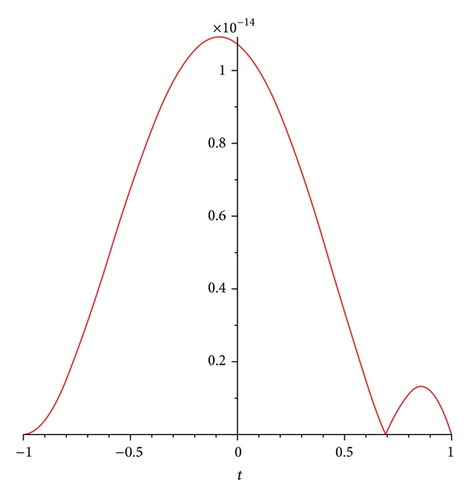
8. Conclusion

In this paper, we presented the composite Chebyshev finite difference method for solving Fredholm integrodifferential equations. The composite ChFD method is indeed an extension of the ChFD scheme with K = 1. This method is based on a hybrid of block-pulse functions and Chebyshev polynomials using Chebyshev-Gauss-Lobatto collocation points.

The useful properties of Chebyshev polynomials and block-pulse functions make it a computationally efficient method to approximate the solution of Fredholm integrodifferential equations. We converted the given problem to a system of algebraic equations using collocation points.

The main advantage of the present method is the ability to represent smooth and especially piecewise smooth functions properly. It was also shown that the accuracy can be improved either by increasing the number of subintervals or by increasing the number of collocation points in subintervals. Several examples have been provided to demonstrate the powerfulness of the proposed method. A comparison was made among the present method, some other well-known approaches, and exact solution which confirms that the introduced method is more accurate and efficient.

Acknowledgment

The authors express their sincere thanks to the referees for the careful and detailed reading of the earlier version of the paper and very helpful suggestions. The authors also gratefully acknowledge that this research was partially supported by the Universiti Putra Malaysia under the ERGS Grant Scheme having Project no. 5527068.

References

1 Polyanin A. D. and Manzhirov A. V., Handbook of Integral Equations, 2008, 2nd edition, Chapman & Hall/CRC, Boca Raton, Fla, USA, https://doi.org/10.1201/9781420010558, MR2404728, ZBL1257.35142.
10.1201/9781420010558
Google Scholar
2 Dehghan M. and Salehi R., The numerical solution of the non-linear integro-differential equations based on the meshless method, Journal of Computational and Applied Mathematics. (2012) 236, no. 9, 2367–2377, https://doi.org/10.1016/j.cam.2011.11.022, MR2879705, ZBL1243.65154.
10.1016/j.cam.2011.11.022
Web of Science® Google Scholar
3 Berenguer M. I., Fernández Muñoz M. V., Garralda-Guillem A. I., and Ruiz Galán M., A sequential approach for solving the Fredholm integro-differential equation, Applied Numerical Mathematics. (2012) 62, no. 4, 297–304, https://doi.org/10.1016/j.apnum.2011.03.009, MR2899247, ZBL1241.65118.
10.1016/j.apnum.2011.03.009
Web of Science® Google Scholar
4 Khani A. and Shahmorad S., An operational approach with Pade approximant for the numerical solution of non-linear Fredholm integro-differential equations, Sharif University of Technology Scientia Iranica. (2011) 19, 1691–1698.
10.1016/j.scient.2012.10.038
Web of Science® Google Scholar
5 Dehghan M. and Saadatmandi A., Chebyshev finite difference method for Fredholm integro-differential equation, International Journal of Computer Mathematics. (2008) 85, no. 1, 123–130, https://doi.org/10.1080/00207160701405436, MR2376026, ZBL1131.65107.
10.1080/00207160701405436
Web of Science® Google Scholar
6 Yalçinbaş S., Sezer M., and Sorkun H. H., Legendre polynomial solutions of high-order linear Fredholm integro-differential equations, Applied Mathematics and Computation. (2009) 210, no. 2, 334–349, https://doi.org/10.1016/j.amc.2008.12.090, MR2509909, ZBL1162.65420.
10.1016/j.amc.2008.12.090
Web of Science® Google Scholar
7 Atabakan Z. P., Kılıçman A., and Nasab A. K., On spectral homotopy analysis method for solving linear Volterra and Fredholm integro-differential equations, Abstract and Applied Analysis. (2012) 2012, 16, 960289, https://doi.org/10.1155/2012/960289.
10.1155/2012/960289
Google Scholar
8 Atabakan Z. P., Nasab A. K., Kılıçman A., and Eshkuvatov K. Z., Numerical solution of nonlinear Fredholm integro-differential equations using Spectral Homotopy Analysis method, Mathematical Problems in Engineering. (2013) 2013, 9, 674364, https://doi.org/10.1155/2013/674364.
10.1155/2013/674364
Web of Science® Google Scholar
9 Lakestani M., Razzaghi M., and Dehghan M., Semiorthogonal spline wavelets approximation for Fredholm integro-differential equations, Mathematical Problems in Engineering. (2006) 12, 96184, https://doi.org/10.1155/MPE/2006/96184, MR2217239, ZBL1200.65112.
10.1155/MPE/2006/96184
Web of Science® Google Scholar
10 Marzban H. R. and Hoseini S. M., A composite Chebyshev finite difference method for nonlinear optimal control problems, Communications in Nonlinear Science and Numerical Simulation. (2012) 18, 1347–1361.
10.1016/j.cnsns.2012.10.012
Web of Science® Google Scholar
11 Marzban H. R. and Hoseini S. M., Solution of linear optimal control problems with time delay using a composite Chebyshev finite difference method, Optimal Control Applications and Methods. (2013) 34, no. 3, 253–274, https://doi.org/10.1002/oca.2019.
10.1002/oca.2019
Web of Science® Google Scholar
12 Canuto C., Hussaini M. Y., Quarteroni A., and Zang T. A., Spectral Methods in Fluid Dynamics, 1988, Springer, Berlin, Germany, MR917480.
10.1007/978-3-642-84108-8
Google Scholar
13 Voigt R. G., Gottlieb D., and Hussaini M. Y., Spectral Methods for Partial Differential Equations, 1984, SIAM, Philadelphia, Pa, USA.
Google Scholar
14 Fox L. and Parker I. B., Chebyshev Polynomials in Numerical Analysis, 1968, Clarendon Press, Oxford, UK, MR0228149.
Google Scholar
15 Behiry S. H. and Hashish H., Wavelet methods for the numerical solution of Fredholm integro-differential equations, International Journal of Applied Mathematics. (2002) 11, no. 1, 27–35, MR1956354, ZBL1029.65146.
Google Scholar
16 Hosseini S. M. and Shahmorad S., Numerical piecewise approximate solution of Fredholm integro-differential equations by the Tau method, Applied Mathematical Modelling. (2005) 29, no. 11, 1005–1021, 2-s2.0-26844574361, https://doi.org/10.1016/j.apm.2005.02.003.
10.1016/j.apm.2005.02.003
Web of Science® Google Scholar
17 Danfu H. and Xufeng S., Numerical solution of integro-differential equations by using CAS wavelet operational matrix of integration, Applied Mathematics and Computation. (2007) 194, no. 2, 460–466, https://doi.org/10.1016/j.amc.2007.04.048, MR2385918, ZBL1193.65216.
10.1016/j.amc.2007.04.048
Web of Science® Google Scholar
18 Darania P. and Ebadian A., A method for the numerical solution of the integro-differential equations, Applied Mathematics and Computation. (2007) 188, no. 1, 657–668, https://doi.org/10.1016/j.amc.2006.10.046, MR2327392, ZBL1121.65127.
10.1016/j.amc.2006.10.046
Web of Science® Google Scholar
19 Yusufoǧlu (Agadjanov) E., Improved homotopy perturbation method for solving Fredholm type integro-differential equations, Chaos, Solitons and Fractals. (2009) 41, no. 1, 28–37, 2-s2.0-67349139225, https://doi.org/10.1016/j.chaos.2007.11.005.
10.1016/j.chaos.2007.11.005
Web of Science® Google Scholar
20 Jiang Z. H. and Schaufelberger W., Block Pulse Functions and Their Applications in Control Systems, 1992, 179, Springer, Berlin, Germany, https://doi.org/10.1007/BFb0009162, MR1169297.
10.1007/BFb0009162
Google Scholar
21 Beauchamp K. G., Applications of Walsh and Related Functions with an Introduction to Sequency Theory, 1984, Academic Press, London, UK, MR772379.
Google Scholar
22 Deb A., Sarkar G., and Sen S. K., Block pulse functions, the most fundamental of all piecewise constant basis functions, International Journal of Systems Science. (1994) 25, no. 2, 351–363, https://doi.org/10.1080/00207729408928964, MR1262500, ZBL0834.42016.
10.1080/00207729408928964
Web of Science® Google Scholar
23 Rao G. P., Piecewise Constant Orthogonal Functions and Their Application to Systems and Control, 1983, Springer, New York, NY, USA, MR791405.
10.1007/BFb0041228
Google Scholar
24 Babolian E. and Masouri Z., Direct method to solve Volterra integral equation of the first kind using operational matrix with block-pulse functions, Journal of Computational and Applied Mathematics. (2008) 220, no. 1-2, 51–57, https://doi.org/10.1016/j.cam.2007.07.029, MR2444153, ZBL1146.65082.
10.1016/j.cam.2007.07.029
Web of Science® Google Scholar
25 Maleknejad K. and Mahmoudi Y., Numerical solution of linear Fredholm integral equation by using hybrid Taylor and block-pulse functions, Applied Mathematics and Computation. (2004) 149, no. 3, 799–806, https://doi.org/10.1016/S0096-3003(03)00180-2, MR2033162, ZBL1038.65147.
10.1016/S0096-3003(03)00180-2
Web of Science® Google Scholar
26 Maleknejad K. and Mahdiani K., Solving nonlinear mixed Volterra-Fredholm integral equations with two dimensional block-pulse functions using direct method, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 9, 3512–3519, https://doi.org/10.1016/j.cnsns.2010.12.036, MR2787798, ZBL1222.65149.
10.1016/j.cnsns.2010.12.036
Web of Science® Google Scholar
27 Maleknejad K., Sohrabi S., and Baranji B., Application of 2D-BPFs to nonlinear integral equations, Communications in Nonlinear Science and Numerical Simulation. (2010) 15, no. 3, 527–535, https://doi.org/10.1016/j.cnsns.2009.04.011, MR2572188, ZBL1221.65339.
10.1016/j.cnsns.2009.04.011
Web of Science® Google Scholar
28 Maleknejad K., Shahrezaee M., and Khatami H., Numerical solution of integral equations system of the second kind by block-pulse functions, Applied Mathematics and Computation. (2005) 166, no. 1, 15–24, https://doi.org/10.1016/j.amc.2004.04.118, MR2145872, ZBL1073.65149.
10.1016/j.amc.2004.04.118
Web of Science® Google Scholar
29 Maleknejad K. and Kajani M. T., Solving second kind integral equations by Galerkin methods with hybrid Legendre and block-pulse functions, Applied Mathematics and Computation. (2003) 145, no. 2-3, 623–629, https://doi.org/10.1016/S0096-3003(03)00139-5, MR2009288, ZBL1101.65323.
10.1016/S0096-3003(03)00139-5
Web of Science® Google Scholar
30 Kılıçman A. and Al Zhour Z. A. A., Kronecker operational matrices for fractional calculus and some applications, Applied Mathematics and Computation. (2007) 187, no. 1, 250–265, https://doi.org/10.1016/j.amc.2006.08.122, MR2323577, ZBL1123.65063.
10.1016/j.amc.2006.08.122
Web of Science® Google Scholar
31 Clenshaw C. W. and Curtis A. R., A method for numerical integration on an automatic computer, Numerische Mathematik. (1960) 2, 197–205, MR0117885, https://doi.org/10.1007/BF01386223, ZBL0093.14006.
10.1007/BF01386223
Google Scholar
32 Elbarbary E. M. E. and El-Kady M., Chebyshev finite difference approximation for the boundary value problems, Applied Mathematics and Computation. (2003) 139, no. 2-3, 513–523, https://doi.org/10.1016/S0096-3003(02)00214-X, MR1948656, ZBL1027.65098.
10.1016/S0096-3003(02)00214-X
Web of Science® Google Scholar
33 Elbarbary E. M. E., Chebyshev finite difference method for the solution of boundary-layer equations, Applied Mathematics and Computation. (2005) 160, no. 2, 487–498, https://doi.org/10.1016/j.amc.2003.11.016, MR2102824, ZBL1059.76043.
10.1016/j.amc.2003.11.016
Web of Science® Google Scholar
34 Yalçınbaş S. and Sezer M., The approximate solution of high-order linear Volterra-Fredholm integro-differential equations in terms of Taylor polynomials, Applied Mathematics and Computation. (2000) 112, no. 2-3, 291–308, https://doi.org/10.1016/S0096-3003(99)00059-4, MR1758715, ZBL1023.65147.
10.1016/S0096-3003(99)00059-4
Web of Science® Google Scholar
35 Akyüz-Daşcioğlu A. and Sezer M., A Taylor polynomial approach for solving high-order linear Fredholm integro-differential equations in the most general form, International Journal of Computer Mathematics. (2007) 84, no. 4, 527–539, https://doi.org/10.1080/00207160701227848, MR2326310, ZBL1118.65129.
10.1080/00207160701227848
Web of Science® Google Scholar

Citing Literature

All articles

On Solution of Fredholm Integrodifferential Equations Using Composite Chebyshev Finite Difference Method

Abstract

1. Introduction

2. Preliminaries and Notations

2.1. Block-Pulse Functions (BPF)

2.2. Chebyshev Polynomials

2.3. Hybrid Functions of Block-Pulse and Chebyshev Polynomials

3. Chebyshev Finite Difference Method

4. Composite Chebyshev Finite Difference Method

5. Convergence Analysis

6. Discretization of Problem

7. Numerical Examples

8. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On Solution of Fredholm Integrodifferential Equations Using Composite Chebyshev Finite Difference Method

Abstract

1. Introduction

2. Preliminaries and Notations

2.1. Block-Pulse Functions (BPF)

2.2. Chebyshev Polynomials

2.3. Hybrid Functions of Block-Pulse and Chebyshev Polynomials

3. Chebyshev Finite Difference Method

4. Composite Chebyshev Finite Difference Method

5. Convergence Analysis

6. Discretization of Problem

7. Numerical Examples

8. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Related

Information