This paper presents an improved nonlinear five-point model capable of analytically describing the electrical behaviors of a photovoltaic module for each generic operating condition of temperature and solar irradiance. The models used to replicate the electrical behaviors of operating PV modules are usually based on some simplified assumptions which provide convenient mathematical model which can be used in conventional simulation tools. Unfortunately, these assumptions cause some inaccuracies, and hence unrealistic economic returns are predicted. As an alternative, we used the advantages of a nonlinear analytical five-point model to take into account the nonideal diode effects and nonlinear effects generally ignored, which PV modules operation depends on. To verify the capability of our method to fit PV panel characteristics, the procedure was tested on three different panels. Results were compared with the data issued by manufacturers and with the results obtained using the five-parameter model proposed by other authors.

1. Introduction

Several methods have been suggested for predicting the behavior of operating photovoltaic (PV) modules. The basis of most of them is the equivalent electrical circuit represented in the simplest way by a current source in parallel with one or many diodes describing the P-N junction. An improved version includes parasitic series and shunt resistances. In general, multidiode representations modeling P-N junctions of PV devices offer accurate results at the expense of long computational time. For simplicity, the single-diode model is used in this paper. This model offers a good compromise between simplicity and accuracy [1, 2] and has been used by numerous authors. It involves the determination of five parameters, namely, photocurrent (I_ph), diode saturation current (I₀), ideality factor (a), parasitic series, and shunt resistances (R_s) and (R_sh), respectively.

Due to the transcendental nature of the I-V relationship for PV modules, significant computation efforts are required to obtain all the related device parameters. One can distinguish the analytical methods which make it possible to calculate independently each parameter according to given limiting conditions [3, 4] and those based on simultaneous determination of a part or all of the set of parameters using algebraic calculations [5]. Iterative calculations have been carried out recently using artificial intelligence (AI) techniques such as fuzzy logic (FL) [6] and artificial neural network (ANN) [7, 8].

However, all these previously proposed models for PV modules pointed out the following assumptions.

(i)
All the connected cells are identical and work under the same conditions of illumination and temperature.
(ii)
The short-circuit current is equivalent to photocurrent and hence proportional to the level of solar irradiation.
(iii)
The variation of open-circuit voltage with irradiance is known to follow a logarithmic function based on an ideal diode equation, and the effect of temperature is due to an exponential increase in the diode saturation current with an increase in temperature.
(iv)
Voltage drops in the conductors connecting the cells are negligible.

However, because the electrical connected solar cells of PV modules are not identical, it is a complex task to predict the I-V characteristic of the whole generator, even if the characteristics of individual cells are known [9]. It should be noted that while previous assumptions will provide convenient mathematical model for use in conventional simulation tools, its validities, and hence its usefulness in understanding the underlying physics, are not guaranteed. Such assumptions cause some deviations in replicating the observed behavior of PV module operating under real condition and often lead to nonphysical variations of device parameters.

The main purpose of this paper is to present an improved methodology for characterizing PV systems. Based on the classical five-point model, amendatory terms are introduced to take into account the effects of nonideal diode parameters and nonlinearity effects that PV module behaviors depend on. Furthermore, series resistance is evaluated using nonlinear fitting of experimental data. Results are compared to experimental data provided by PV modules manufacturers and an existing model.

2. Theory and Analysis

2.1. PV Module Model

An ideal PV module consists of a single diode connected in parallel with a light generated current source (I_ph) as shown in Figure 1. The current-voltage (I-V) relationship is taken to be the Shockley-type single exponential I-V characteristic with ideality factor written as

(1)

The thermal voltage is given by V_T = N_s K T_c/q, where N_s, K, T_c, and q represent the number of cells in series, the Boltzmann constant, the temperature of the cells, and elementary charge, respectively.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Ideal PV circuit model.

Equation (1) does not represent any existing photovoltaic device; practical applications included both the parasitic series and shunt resistances, as it can be seen in Figure 2, to represent internal losses caused by the interconnections of cells and leakage current in the junctions, respectively. An output current equation can be written as

(2)

To account for the highly nonlinear weather dependence of PV device, more parameters describing environmental influence on each component should be introduced in the nonlinear model for each component [10–14]. However, as given in (2), it can be an arduous work to associate factors of nonlinear dependence on weather parameters to each device parameter, due to their lumped nature of multiple physical phenomena representative. In [10], 13 parameters are introduced for the nonlinear components of the circuit model. This requires extensive computation to extract the parameters due to the highly nonlinear characteristics of most components and the complexity of the resulting equation. In this work, nonlinear five-point model is used as an alternative method.

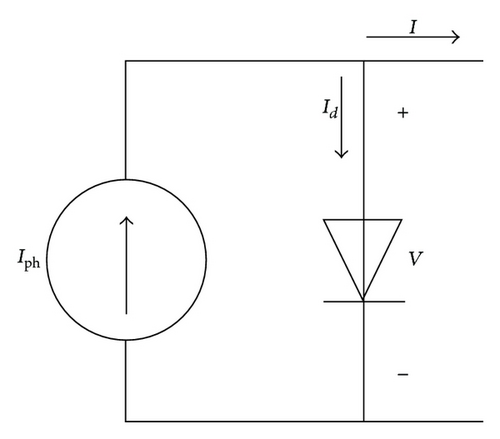
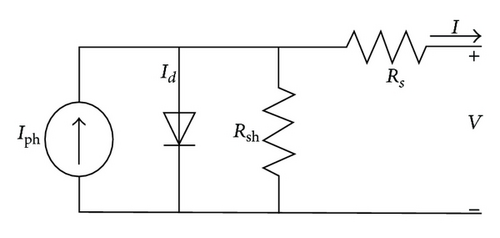
2.2. Nonlinear Five-Point Model

The five-point model is an analytical method to extract related device parameters from values of key operational quantities measured from well-defined points of I-V characteristic, namely, the open circuit voltage V_oc, the short-circuit current I_sc, the voltage at maximum power point V_mp, the current at maximum power point I_mp, the slope at open-circuit point , and the slope at short-circuit point [14–17]. Using this method, the additional terms that account for nonlinear effects are not directly associated with expressions of related device parameters, but they are allocated to the key operational quantities abovementioned. This approach makes it possible to adequately tame the concept of nonlinearity in well-known point of I-V characteristic in order to make device parameters depend on easily used pieces of information derived from operational PV module.

2.2.1. Calculating Key Operational Quantities

Analyses of outdoor tested PV module result in some deviations of short-circuit current from its linearity with solar irradiance G (W/m²). A power law having an exponent α is introduced to take into account the nonlinear effects that the short-circuit current depends on. In addition to temperature dependence, short-circuit current can be written as

(3)

where

is the thermal coefficient of short-circuit current (A/K).

The evaluation of the open-circuit voltage based on an ideal diode equation leads to difficulties in replicating the behaviors of tested PV modules. Additional terms or some correction coefficients must be introduced to account for the shunt resistance, series resistance, and the nonideality of the diode. Based on the model given by Van Dyk et al. [18] and then taking into account the effect of temperature, the open-circuit voltage Voc at any given conditions can be expressed by

(4)

where V_oc and

are the open-circuit voltage of the PV module under the normal solar irradiance G and the standard solar irradiance G₀, respectively; β is a PV module technology specific-related dimensionless coefficient [18]; and γ is the exponent considering all the nonlinear temperature-voltage effects [11].

Electric generators are generally classified as current or voltage sources. The practical PV device presents a hybrid behavior, which may be of current or voltage source depending on the operating point [2]. Furthermore, the maximum power point appears to be a compromise of the hybrid behavior of the cell between both voltage and current source regions [19]. At this particular point, current varies like the high currents of the module, whereas its voltage follows the variation of the high voltages. Equation (5) are proposed to describe these effects:

(5)

The subscript mp refers to maximum power point.

Nominal parasitic resistances

and

are defined for STC as follows:

(6)

(7)

They are the reciprocals of the slopes at the open-circuit point and short-circuit point, respectively. The values of these resistances are not usually provided by module manufacturers. The precise determination of

and

requires experimentation under certain conditions of irradiance and temperature to get enough (I- V) data around the points of short circuit and open circuit. Given the difficulty associated with determining the slope at different points along the I-V curve, the values of

are set in the range [0.15 Ω, 0.35 Ω] for crystalline silicon material PV modules, whereas (6) is used for thin-film type PV modules. In turn,

is used as a fitting parameter to better describe the adaptation of the model to the effect of changes in operating conditions for a given solar module.

2.2.2. Calculating Related Device Parameters

Beyond the core losses related to the selective absorption of light and recombination, there are significant energy degradations due to parasitic resistances. Resistive effects in solar cells reduce efficiency by dissipating power in the resistance. Making their evaluation based on operating conditions is extremely important for studying the electrical behaviors of photovoltaic devices.

The series resistance of solar cell is a parameter of particular interest because of its influence on the maximum available power and the fill factor. It is also a parameter that indicates in some way the quality of device and can be used as production test [20]. The series resistance that represents the structural resistance of the PV module has three causes: firstly, the movement of current through the emitter and base of the solar cell; secondly, the contact resistance between the metal contact and the semiconductor; and finally, the resistance of the top and rear metal contacts [21]. Its main impact on the I-V characteristic is restricted in the voltage-source region, at the vicinity of the open-circuit voltage, although exclusively high values may also reduce the short-circuit current. Various techniques have been used to determine R_s [15, 16, 20, 22, 23]. In this work, some techniques have been combined; the slope method leads to R_s determination with no limiting approximations and is generally considered to give good results [16]. This permits us to write R_s as follows:

(8)

Considering the asymptotic behavior of the I-V curve at short- and open-circuit conditions [19], (8) can be calculated as

(9)

More generally,

(10)

Reich et al. [24] noticed that apparent series resistance in PV module follows similar power law with solar irradiance. However, similar to the statement in [24], such calculated series resistances do not reflect physical analysis. In order to bring further improvements, several empirical formulas were tested based on complete curve fitting of the solar module I-V equation to experimental I-V curves provided by module manufacturers; the best adjustments are obtained only for negative values of α; therefore, (11) is rewritten as

(11)

In turn, the shunt resistance (R_sh) is due to the P-N junction nonidealities and impurities near the junction, which cause partial shorting of the junction, especially near the edges of the cell [21]. The effect of R_sh occurs at small voltages such that the diode current is small compared to the shunt current [25]. Apparent observations, from examinations of the slopes of the I-V curves at short-circuit conditions based on the experimental data, show that the effective shunt resistance increases (and the slope thus decreases) as absorbed radiation is reduced [5, 16]. The following equation is proposed to describe this effect:

(12)

To evaluate the last three related device parameters, three independent pieces of information are needed. The former pieces of information are found on several points of I-V characteristic curves. It has to be noted that the I-V curve is highly nonlinear, and any wrongly selected points may result in significant errors [26]. In this work, these parameters are evaluated using correlations for the current and the voltage around key operational points: the short-circuit point, the open-circuit point, and the maximum power point. These correlations give three independent pieces of information resulting in (13)–(15).

At short-circuit point, V = 0, I = I_sc:

(13)

At the open-circuit point, I = 0, V = V_oc:

(14)

At maximum power point MPP, I = I_mp, V = V_mp:

(15)

Rearranging (13) gives I_ph as

(16)

Combining (13) and (14) gives I₀ as follows:

(17)

Similarly, combining (14) and (15), the ideality factor a is expressed as follows:

(18)

2.2.3. Calculation of the Constants

The constants α, β, and γ are related to important effects in the photovoltaic module. They are empirical and the precision of the model depends on the acuity of their calculated results. Accurate determination of these constants requires significant experimentation to find the values of current and voltage at different points for different operating conditions, in order to calculate them from the following relationship:

(19)

The indices 1 and 2 are related to the fact that these quantities have to be measured for two different operating conditions.

The variation of the open-circuit voltage is related to the variations of the solar radiation intensity and cells temperature. To calculate β, temperature is kept constant and irradiance varies from G₁ to G₂. β is obtained as

(20)

For one value of irradiance, the temperature of the cells varies from T₁ to T₂, and γ is obtained as follows:

(21)

3. Results and Discussions

The capabilities of the nonlinear five-point model to predict the electrical response of PV devices is validated by measured experimental data of selected PV modules. Three PV modules of different technologies are used for investigation; these include monocrystalline, multicrystalline and thin-film types, namely, Shell SM55, Shell S75, and Shell ST40, respectively. The experimental data were extracted from manufacturer’s data sheet [27]. The specifications of these modules are summarized in Table 1.

Table 1. Specifications for the three modules used in the experiments.

Parameter	Monocrystalline (Si) SM55	Multicrystalline (Si) S75	Thin-film (CIS) ST40
I_sc (A)	3.45	4.7	2.68
V_oc (V)	21.7	21.6	23.3
I_mp (A)	3.15	4.26	2.41
V_mp (V)	17.4	17.6	16.6
(mA/°C)	1.4	2	0.35
(mV/°C)	−76	−76	−100
N_s	36	36	42

By applying the nonlinear five-point model described in the previous subsection, the computed results of selected PV modules are obtained. The procedure was executed for various irradiance and temperature levels. To evaluate the accuracy of the proposed model, the results obtained are compared to the five-parameter model described in [28].

The constants α, β, and γ can be calculated following the constant estimation procedures given above. The results are shown in Table 2.

Table 2. Constants estimation for PV modules.

Constant	α	β	γ
Monocrystalline SM55	0.984	0.058	1.064
Multicrystalline S75	0.996	0.052	1.155
Thin-film ST40	0.998	0.087	1.343

In Figures 3 and 4 the I-V characteristic curves evaluated using the proposed model are compared to the experimental data issued by manufacturer. The I-V curves of the five-parameter model are not shown for brevity. It can be seen that Figures 2 and 3 show a good agreement between the I-V curves obtained by proposed model and the provided experimental data for all types of modules in various operating conditions analyzed. In particular, the proposed model is very accurate at low irradiance levels. In turn, some little inaccuracies still occur for voltages greater than the maximum power voltage when subjected to temperature variation.

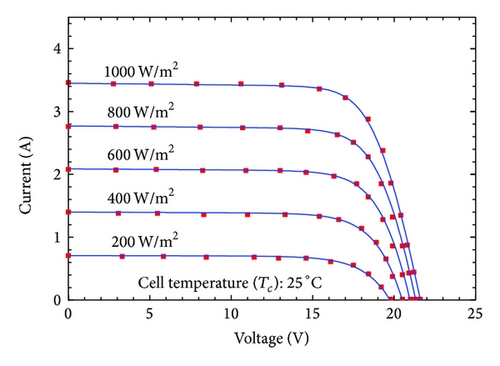
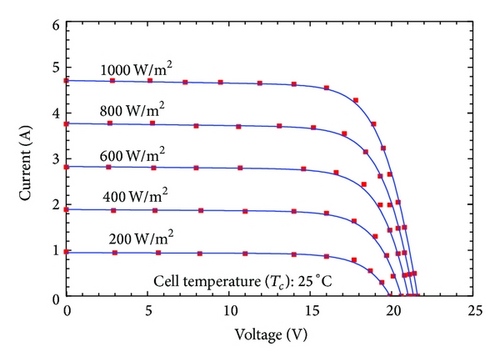
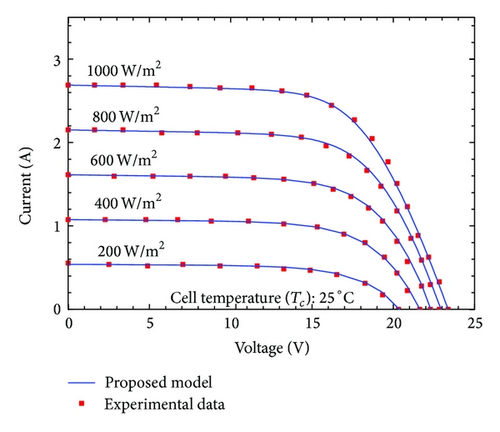
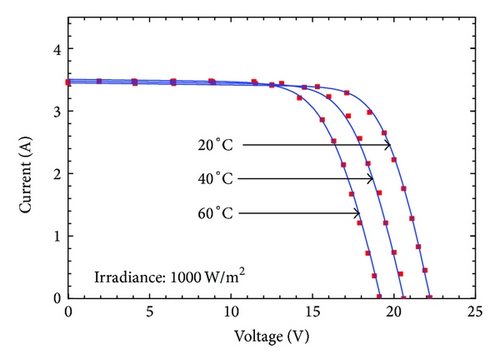
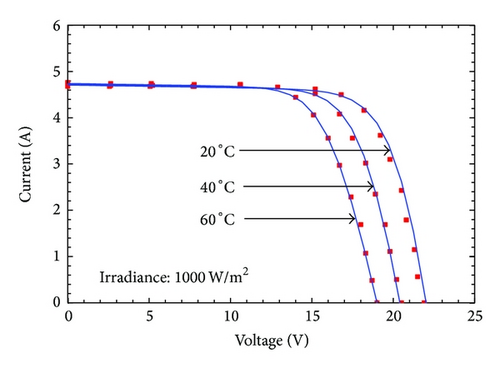
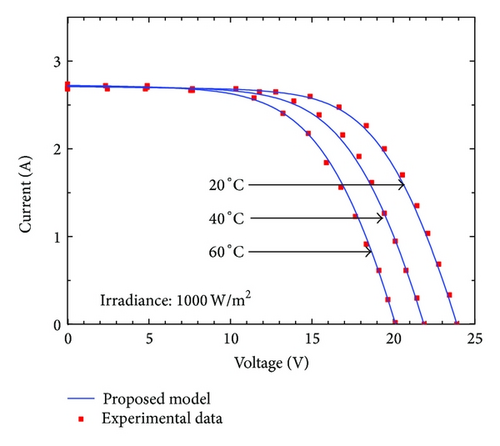
Table 3 lists the values of the related device parameters computed using the proposed and the five-parameter models for various levels of irradiance. It can be noticed, using the five-parameter model, that the constant values of the parameters a, I₀, and R_s are obtained when subjected to irradiance variation. This is foreseeable, since the model assumes these parameters to be invariant regardless of irradiance variations. However, the proposed model formulates irradiance dependence for all parameters. Logically, the five-point model can be considered more accurate because the shunt resistance decreases and the series resistance increases with increasing irradiance as stipulated in [29, 30]; the diode ideality factor decreases with increasing irradiance as described in [30, 31].

Table 3. Parameters for the proposed model.

Parameter	Monocrystalline SM55		Multicrystalline S75		Thin-film ST40
Parameter	Proposed model	Five-parameter model	Proposed model	Five-parameter model	Proposed model	Five-parameter model
1000 W/m²
I_ph (A)	3.453	3.457	4.715	4.715	2.702	2.694
I₀ (A)	9.721E − 8	9.906E − 7	9.193E − 8	2.430E − 7	3.463E − 7	4.174E − 6
a	1.338	1.183	1.311	1.388	1.361	1.75
R_s (Ω)	0.3	0.3625	0.2	0.1281	1.3	0.7457
R_sh (Ω)	350	186.5	179	127.4	250	140.8

800 W/m²
I_ph (A)	2.771	2.765	3.774	3.772	2.157	2.155
I₀ (A)	5.398E − 7	9.906E − 7	3.961E − 7	2.430E − 7	2.994E − 6	4.174E − 6
a	1.486	1.183	1.432	1.388	1.571	1.75
R_s (Ω)	0.2371	0.3625	0.1283	0.1281	1.02	0.7457
R_sh (Ω)	436	233.1	223.6	159.2	312.5	175.9

600 W/m²
I_ph (A)	2.087	2.074	2.832	2.829	1.616	1.617
I₀ (A)	1.624 E − 6	9.906E − 7	9.402E − 7	2.430E − 7	13.64E − 6	4.174E − 6
a	1.606	1.183	1.519	1.388	1.771	1.75
R_s (Ω)	0.1762	0.3625	0.117	0.1281	0.7465	0.7457
R_sh (Ω)	578.7	310.8	297.8	212.3	416.7	234.6

400 W/m²
I_ph (A)	1.4	1.383	1.89	1.886	1.076	1.075
I₀ (A)	3.134E − 6	9.906E − 7	1.386E − 6	2.43E − 7	37.685E − 6	4.174E − 6
a	1.698	1.183	1.512	1.388	1.95	1.75
R_s (Ω)	0.1155	0.3625	0.07654	0.1281	0.4813	0.7457
R_sh (Ω)	862.5	466.1	446.1	318.5	625	351.9

200 W/m²
I_ph (A)	0.707	0.6913	0.9473	0.9429	0.5377	0.5388
I₀ (A)	4.071 E − 6	9.906E − 7	1.219E − 6	2.430E − 7	60.709E − 6	4.174E − 6
a	1.763	1.183	1.582	1.388	2.085	1.75
R_s (Ω)	0.05624	0.3625	0.03706	0.1281	0.2278	0.7457
R_sh (Ω)	1706	932.3	890	636.9	1250	703.8

The computed parameters using the proposed and the five-parameter models for temperature variation are shown in Table 4. Once again, the constant values of the parameters a, R_s, and R_sh are obtained when temperature variation is considered. These are undoubtedly sources of inaccuracies. In turn, the proposed model is consistent with open literature; the diode ideality factor decreases with increasing temperature as issued in [32–34], and the series resistance R_s decreases with increasing temperature which agrees with the work in [35], although its variation rate is more important.

Table 4. Parameters for the proposed model (G = 1000 W/m²).

Parameter	Monocrystalline SM55		Multicrystalline S75		Thin-film ST40
Parameter	Proposed model	Five-parameter model	Proposed model	Five-parameter model	Proposed model	Five-parameter model
60°C
I_ph (A)	3.502	3.507	4.744	4.73	2.712	2.706
I₀ (A)	103.914E − 9	6.512E − 7	110.675E − 9	9.058E − 6	4.381E − 6	108.657E − 6
a	1.067	1.183	1.042	1.388	1.064	1.614
R_s (Ω)	0.2625	0.3625	0.1747	0.1281	1.114	0.7457
R_sh (Ω)	350	186.5	179	127.4	250	140.8

40°C
I_ph (A)	3.474	3.478	4.728	4.721	2.706	2.699
I₀ (A)	100.294E − 9	6.649E − 8	100.308E − 9	1.259E − 6	3.868E − 7	18.365E − 6
a	1.211	1.183	1.185	1.388	1.221	1.614
R_s (Ω)	0.2828	0.3625	0.1884	0.1281	1.214	0.7457
R_sh (Ω)	350	186.5	179	127.4	250	140.8

20°C
I_ph (A)	3.446	3449	4.711	4.712	2.7	2.692
I₀ (A)	96.036E − 9	5.037E − 9	89.039E − 9	1.355E − 7	3.324E − 7	2.467E − 6
a	1.385	1.183	1.357	1.388	1.413	1.614
R_s (Ω)	0.3061	0.3625	0.2042	0.1281	1.331	0.7457
R_sh (Ω)	350	186.5	179	127.4	250	140.8

These related device parameters are strongly influenced by the irradiance and temperature. However, computed parameters using the five-parameter model present an obsolete dependence to the variation of environmental conditions. It is obvious that the use of constant parameters determined under STC must bring deviations in replicating the observed behavior of PV module in other operating conditions [28, 29]. Logically, values of related device parameters computed using the five-point model can be considered to be appropriately calculated. Its formulation is based on the PV module operation with the particularity to point out important effects of nonlinearities that environmental variations of parameters depend on. Furthermore, values of these parameters are realistic and in close agreement with results published elsewhere as it has been noticed previously.

For the thin-film type PV module, particularly large values of ideality factor are obtained in low irradiance due to decreasing series resistance. Theoretical approaches predict diode ideality factors in a range 1 < a < 2 dependent on the energy of the recombination center and the respective capture cross sections for electrons and holes. The explanation of a > 2 obtained when G = 200 W/m² is not possible by considering recombination via a single recombination center [36]. However, certain process like the tunneling enhanced recombination applied to thin-film technologies predicts ideality factor that may exceed 2 [36, 37]. The proposed model is based on the operation of PV module with absence of simplification and may lump one or multiple steps recombination process via a series of trap states distributed in space and energy that can result in such large ideality factor.

To provide a clear picture of the precision of the proposed model, the errors using the proposed and five-parameter models are computed. The absolute error is defined as the absolute difference between the experimental and computed current values of the I-V curves for a given voltage point. These calculations are carried out for various irradiance and temperature levels as shown in Figures 5 and 6, respectively.

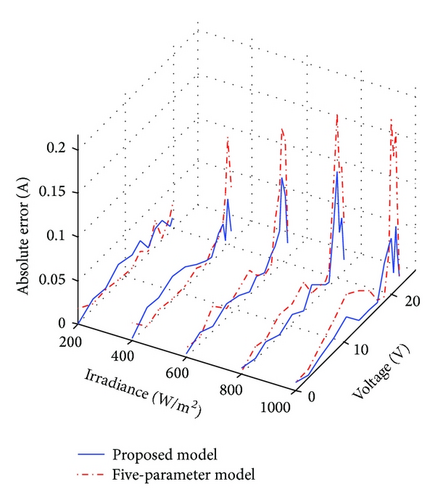
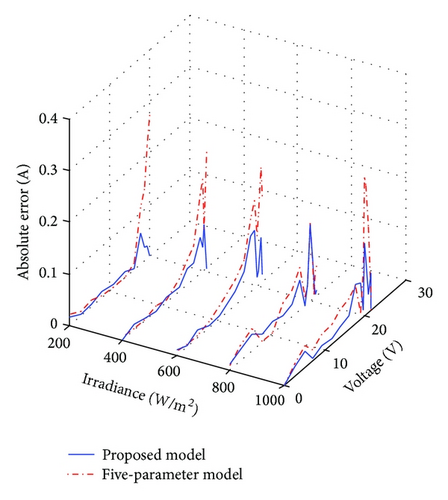
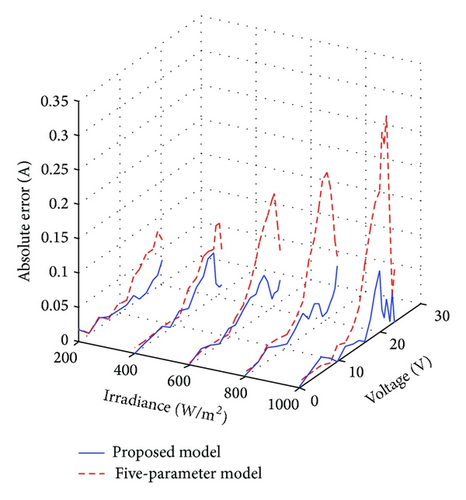
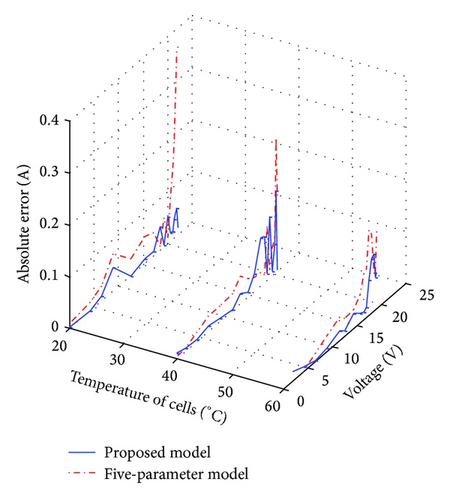
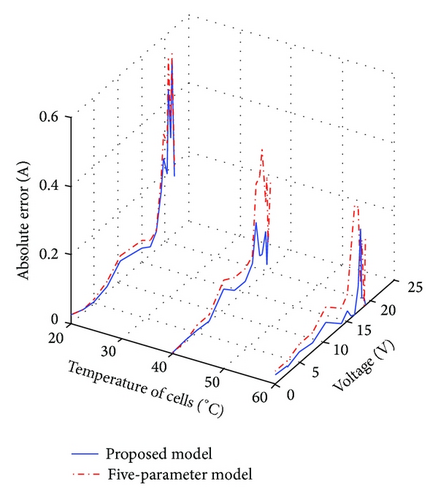
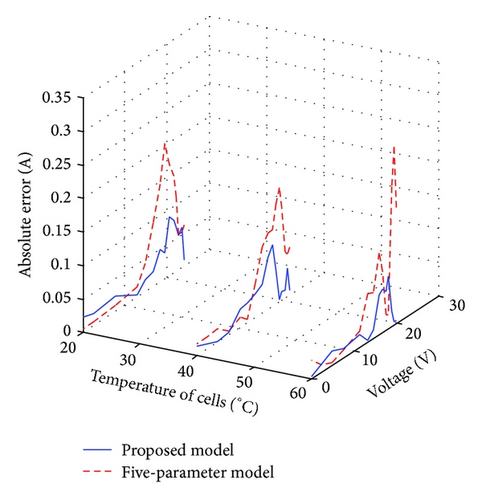
The proposed model globally shows fewer errors than the five-parameter model for various environmental conditions analyzed. This is expected because values of many related device parameters computed using the five-parameter model do not vary with variation of environmental conditions as shown in Tables 3 and 4. However, for proposed model, values of parameters vary with irradiance and temperature. This means that the proposed model taking into account the nonlinear effects leads to appropriate computed parameters.

In most cases, exceptionally high errors occur near the vicinity of MPP. This is ascribable to the fact that the value of the series resistance plays a dominant role in determining the curvature of the I-V curve [34]. For the five-parameter model, constant value of R_s when irradiance and temperature vary results to inaccurate I-V curves in this region. On the other hand, in addition to the nonlinear effects, the determination of R_s using the proposed model is based on complete fitting of experimental data. Thus, the series resistance is adequately computed, and hence the error of the nonlinear five-point model is reduced.

4. Conclusion

In this paper, modeling of electrical response of PV modules using an analytical nonlinear five-point model is described. Unlike the previous models suggested by other researchers, the proposed model computes the PV module parameters at any irradiance and temperature point, using only the datasheet information for a PV module. The accuracy of the proposed model is evaluated using experimental data from the manufacturers of three PV modules of different types. Its performance is compared to a popular five-parameter model. The observed superior accuracy of the proposed model to describe these PV modules behaviors suggests that this proposed model might also represent an even better phenomenological description of the electrical mechanisms prevalent in these particular devices and the nonlinear effects that they depend on. In addition, research on analysis and replication of operation of these specific devices in terms of the proposed model is currently being carried out, but the interest and scope of the proposed nonlinear five-point model is noteworthy. Beyond its simplicity of implementation, the proposed model adequately describes the evolution of these specific devices physical phenomena when subjected to temperature and irradiance variations, and hence it is envisaged that the proposed model can be a valuable design tool for PV system during the production as well as during the use.

Symbols

a:: Ideality factor
CIS:: Copper indium selenide material
G:: Irradiance
I:: Current
MPP:: Maximum power point
R:: Resistance
STC:: Standard test conditions
V:: Voltage
I₀:: Saturation current
I_ph:: Photocurrent
Si:: Silicon material
V_T:: Thermal voltage
N_s:: Number of cells in series
V_oc:: Open-circuit voltage
I_sc:: Short-circuit current

Subscript

ref:: Reference conditions
mpp:: Maximum power point
oc:: Open-circuit
s:: Series
sc:: Short-circuit
sh:: Shunt.

Greek Letters

μ:: Temperature coefficient
α:: Constant
β:: Constant
γ:: Constant.

Conflict of Interests

There is no competing interests in the validity of this paper due to the choice of the Shell SM55 and Shell SP5 modules.

Acknowledgments

The authors are grateful to Dr. Obounou, Dr. Akana, and Miss Enoh for their efforts in the realization of this work.

References

1 Carrero C., Amador J., and Arnaltes S., A single procedure for helping PV designers to select silicon PV modules and evaluate the loss resistances, Renewable Energy. (2007) 32, no. 15, 2579–2589, 2-s2.0-35548938229, https://doi.org/10.1016/j.renene.2007.01.001.
Google Scholar
2 Villalva M. G., Gazoli J. R., and Filho E. R., Comprehensive approach to modeling and simulation of photovoltaic arrays, IEEE Transactions on Power Electronics. (2009) 24, no. 5, 1198–1208, 2-s2.0-67349141404, https://doi.org/10.1109/TPEL.2009.2013862.
Google Scholar
3 Celik A. N. and Acikgoz N., Modelling and experimental verification of the operating current of mono-crystalline photovoltaic modules using four- and five-parameter models, Applied Energy. (2007) 84, no. 1, 1–15, 2-s2.0-33749242233, https://doi.org/10.1016/j.apenergy.2006.04.007.
Google Scholar
4 Arab A. H., Chenlo F., and Benghanem M., Loss-of-load probability of photovoltaic water pumping systems, Solar Energy. (2004) 76, no. 6, 713–723, 2-s2.0-1642346983, https://doi.org/10.1016/j.solener.2004.01.006.
Google Scholar
5 De Soto W., Klein S. A., and Beckman W. A., Improvement and validation of a model for photovoltaic array performance, Solar Energy. (2006) 80, no. 1, 78–88, 2-s2.0-29144478675, https://doi.org/10.1016/j.solener.2005.06.010.
Web of Science® Google Scholar
6 Elshatter T. F., Elhagree M. E., Aboueldahab, and Elkousry A. A., Fuzzy modeling and simulation of photovoltaic system, Proceedings of the 14th European Photovoltaic Solar Energy Conference, 1999, Barcelona, Spain.
Google Scholar
7 Mellit A., Benghanem M., and Kalogirou S. A., Modeling and simulation of a stand-alone photovoltaic system using an adaptive artificial neural network: proposition for a new sizing procedure, Renewable Energy. (2007) 32, no. 2, 285–313, 2-s2.0-33748420215, https://doi.org/10.1016/j.renene.2006.01.002.
Google Scholar
8 Celik A. N., Artificial neural network modelling and experimental verification of the operating current of mono-crystalline photovoltaic modules, Solar Energy. (2011) 85, no. 10, 2507–2517, 2-s2.0-80052289721, https://doi.org/10.1016/j.solener.2011.07.009.
Google Scholar
9 Lorenzo E., Solar Electricity: Engineering of Photovoltaic Systems, 1994, Progensa.
Google Scholar
10 Gow J. A. and Manning C. D., Development of a photovoltaic array model for use in power-electronics simulation studies, IEE Proceedings: Electric Power Applications. (1999) 146, no. 2, 193–200, 2-s2.0-0032629423, https://doi.org/10.1049/ip-epa:19990116.
Google Scholar
11 Zhou W., Yang H., and Fang Z., A novel model for photovoltaic array performance prediction, Applied Energy. (2007) 84, no. 12, 1187–1198, 2-s2.0-34548335144, https://doi.org/10.1016/j.apenergy.2007.04.006.
Web of Science® Google Scholar
12 Asif S. and Li Y., Solar cell modeling and parameter optimization using simulated annealing, Journal of Propulsion and Power. (2008) 24, no. 5, 1018–1022, 2-s2.0-54549110079, https://doi.org/10.2514/1.35037.
Google Scholar
13 Maffezzoni P. and D′Amore D., Compact electrothermal macromodeling of photovoltaic modules, IEEE Transactions on Circuits and Systems II. (2009) 56, no. 2, 162–166, 2-s2.0-62749115979, https://doi.org/10.1109/TCSII.2008.2011612.
Google Scholar
14 Bogning Dongue S., Njomo D., and Ebengai L., A new strategy for accurately predicting I-V electrical characteristics of PV modules using a nonlinear five-point model, Journal of Energy. (2013) 2013, 8, 321694.
10.1155/2013/321694
Google Scholar
15 Chan D. and Phang J., Analytical methods for the extraction of solar-cell single- and double-diode model parameters from I-V characteristics, IEEE Transactions on Electron Devices. (1987) 34, no. 2, 286–293, 2-s2.0-0023292133.
Google Scholar
16 Schroder D. K., Semiconductor Material and Device Characterization, 1998, John Willey & Sons, New York, NY, USA.
Google Scholar
17 Chegaar M., Ouennoughi Z., Guechi F., and Langueur H., Determination of solar cells parameters under illuminated conditions, Journal of Electron Devices. (2003) 2, 17–21.
Google Scholar
18 van Dyk E. E., Meyer E. L., Vorster F. J., and Leitch A. W. R., Long-term monitoring of photovoltaic devices, Renewable Energy. (2002) 25, no. 2, 183–197, 2-s2.0-0036462276, https://doi.org/10.1016/S0960-1481(01)00064-7.
Google Scholar
19 Saloux E., Teyssedou A., and Sorin M., Explicit model of photovoltaic panels to determine voltages and currents at the maximum power point, Solar Energy. (2011) 85, no. 5, 713–722, 2-s2.0-79954584248, https://doi.org/10.1016/j.solener.2010.12.022.
Google Scholar
20 Casbestany J. and Castener L., A simple solar cell series resistance measurement method, Revue de Physique Appliquée. (1983) 18, no. 9, 565–587.
Google Scholar
21 Wenham S. R., Green M. A., Watt M. E., and Corkish R., Applied Photovoltaics, 2007, 2nd edition, ARC Centre for Advanced Silicon Photovoltaics and Photonics.
Google Scholar
22 Jia Q., Anderson W. A., Liu E., and Zhang S., A novel approach for evaluating the series resistance of solar cells, Solar Cells. (1988) 25, no. 3, 311–318, 2-s2.0-0024132347.
Google Scholar
23 Bashahu M. and Habyarimana A., Review and test of methods for determination of the solar cell series resistance, Renewable Energy. (1995) 6, no. 2, 129–138, 2-s2.0-0029276311.
Google Scholar
24 Reich N. H., van Sark W. G. J. H. M., Alsema E. A., Lof R. W., Schropp R. E. I., Sinke W. C., and Turkenburg W. C., Crystalline silicon cell performance at low light intensities, Solar Energy Materials and Solar Cells. (2009) 93, no. 9, 1471–1481, 2-s2.0-67649622006, https://doi.org/10.1016/j.solmat.2009.03.018.
Google Scholar
25 Fahrenbruch A. L. and Bube R. H., Fundamentals of Solar Cells, 1983, Academic Press, New York, NY, USA.
Google Scholar
26 Ishaque K., Salam Z., Mekhilef S., and Shamsudin A., Parameter extraction of solar photovoltaic modules using penalty-based differential evolution, Applied Energy. (2012) 99, 297–308.
Google Scholar
27 Shell, Shell Solar Product Information Sheet, http://www.solarcellsales.com/techinfo/technical_docs.cfm.
Google Scholar
28 Dongue S. B., Njomo D., Tamba J. G., and Ebengai L., Modeling of electrical response of illuminated crystalline photovoltaic modules using four- and five-parameter models, International Journal of Emerging Technologies and Advanced Engineering. (2012) 2, no. 11, 612–619.
Google Scholar
29 Eikelboom J. A. and Reinders A. H., Determination of the irradiation dependent efficiency of multicrystalline Si PV modules on basis of IV curve fitting and its influence on the annual performance, Proceedings of the 14th European PV Solar Energy Conference, 1997, Barcelona, Spain, 293–296.
Google Scholar
30 Kassis A. and Saad M., Analysis of multi-crystalline silicon solar cells at low illumination levels using a modified two-diode model, Solar Energy Materials and Solar Cells. (2010) 94, no. 12, 2108–2112, 2-s2.0-77957653249, https://doi.org/10.1016/j.solmat.2010.06.036.
Google Scholar
31 Bätzner D. L., Romeo A., Zogg H., and Tiwari A. N., CdTe/CdS solar cell performance under low irradiance, Proceedings of the 17th European Photovoltaic Solar Energy Conference and Exhibition, 2001, Munich, Germany.
Google Scholar
32 Sites J. R. and Mauk P. H., Diode quality factor determination for thin-film solar cells, Solar Cells. (1989) 27, no. 1–4, 411–417, 2-s2.0-0024755084.
Google Scholar
33 Sharma S. K., Samuel K. B., Srinivasamurthy N., and Agrawal B. L., Overcoming the problems in determination of solar cell series resistance and diode factor, Journal of Physics D. (1990) 23, no. 9, 1256–1260, 2-s2.0-0025485156, https://doi.org/10.1088/0022-3727/23/9/019.
Google Scholar
34 Ishaque K. and Salam Z., An improved modeling method to determine the model parameters of photovoltaic (PV) modules using differential evolution (DE), Solar Energy. (2011) 85, no. 9, 2349–2359, 2-s2.0-80051597713, https://doi.org/10.1016/j.solener.2011.06.025.
Google Scholar
35 Singh P., Singh S. N., Lal M., and Husain M., Temperature dependence of I-V characteristics and performance parameters of silicon solar cell, Solar Energy Materials and Solar Cells. (2008) 92, no. 12, 1611–1616, 2-s2.0-55349141740, https://doi.org/10.1016/j.solmat.2008.07.010.
Google Scholar
36 Abou-Ras D., Kirchartz T., and Rau U., Advanced Characterization Techniques for Thin Film Solar Cells, 2011, Wiley-VCH, Weinheim, Germany.
Google Scholar
37 Rau U., Tunneling-enhanced recombination in Cu(In, Ga)Se2 heterojunction solar cells, Applied Physics Letters. (1999) 74, no. 1, 111–113, 2-s2.0-0000716071, https://doi.org/10.1063/1.122967.
Google Scholar

Citing Literature

All articles

An Improved Nonlinear Five-Point Model for Photovoltaic Modules

Abstract

1. Introduction

2. Theory and Analysis

2.1. PV Module Model

2.2. Nonlinear Five-Point Model

2.2.1. Calculating Key Operational Quantities

2.2.2. Calculating Related Device Parameters

2.2.3. Calculation of the Constants

3. Results and Discussions

4. Conclusion

Symbols

Subscript

Greek Letters

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley