This paper introduces the stability and convergence of two-step Runge-Kutta methods with compound quadrature formula for solving nonlinear Volterra delay integro-differential equations. First, the definitions of (k, l)-algebraically stable and asymptotically stable are introduced; then the asymptotical stability of a (k, l)-algebraically stable two-step Runge-Kutta method with 0 < k < 1 is proved. For the convergence, the concepts of D-convergence, diagonally stable, and generalized stage order are firstly introduced; then it is proved by some theorems that if a two-step Runge-Kutta method is algebraically stable and diagonally stable and its generalized stage order is p, then the method with compound quadrature formula is D-convergent of order at least min{p, ν}, where ν depends on the compound quadrature formula.

1. Introduction

Volterra delay integro-differential equations (VDIDEs) arise widely in the mathematical modeling of physical and biological phenomena. Significant advances in the theoretical analysis and in the numerical analysis for these problems have been made in the last few decades (see, e.g., [1, 2]). For the case of linear stability and convergence for these equations, numerical time-integration techniques of one-step collocation and Runge-Kutta type were investigated in [3–8]. Linear multistep-based methods were studied in [9–12]. De la Sen and Luo studied the uniform exponential stability of a wide class of linear time-delay systems in [13]; De la Sen considered the stability of impulsive time-varying systems in [14].

For the case of nonlinear stability and convergence, stability results were obtained in [15, 16], where the authors investigated the nonlinear stability of continuous Runge-Kutta methods, discrete Runge-Kutta methods, and backward differentiation (BDF) methods, respectively. However, most of these important results are based on the classical Lipschitz conditions, while the classical Lipschitz conditions are so strong that there are few equations satisfying them. Most of the Volterra delay integro-differential equations satisfy the one-sided Lipschitz condition, while the studies focusing on the stability and convergence of the numerical method for nonlinear VDIDEs based on a one-sided Lipschitz condition have not yet been seen in the literature. By means of a one-sided Lipschitz condition, we will discuss the stability and convergence of two-step Runge-Kutta (TSRK) methods for nonlinear VDIDEs in the present paper.

The paper is organized as follows. In Section 2, a fairly general class of VDIDEs is defined. We present a stability criterion for such problems, which generalizes the criteria in the above references. A class of two-step Runge-Kutta methods is also derived for solving VDIDEs. They are obtained by compound quadrature rules. In Sections 3 and 4, nonlinear stability and convergence of TSRK method for NDDEs are derived and proved. In Section 5 we present some numerical examples in order to illustrate the nonlinear stability and convergence of a two-step Runge-Kutta method. These numerical results show that the new methods are quite effective.

2. A Class of VDIDES and the Two-Step Runge-Kutta Methods

It is the purpose of this paper to investigate the nonlinear stability and convergence properties of the following initial-value problem VDIDEs:

()

where f, g, and φ are smooth enough such that (1) has a unique solution y(t) and τ is a positive delay term. We assume that there exist some inner product 〈·, ·〉 and the induced norm ||·|| in C^N, such that φ : [−τ, 0] → C^N and f : [0, Τ] × C^N × C^N × C^N → C^N satisfy the following conditions:

()

for t ∈ [0, Τ], D = {(t, v) : t ∈ [0, Τ), v ∈ [t − τ, t]}, and for all u₁, u₂, v₁, v₂, w₁, w₂ ∈ C^N(−α), β, σ, and γ are nonnegative constants.

Throughout this paper, we assume that (1) has unique solution y(t) and denote the problem class R(α, β, σ, γ) that consist problem of type (1) with (2)–(4). In order to make the error analysis feasible, we always assume that (1) has a unique solution y(t) which is sufficiently differentiable and satisfies

()

For function g(t, θ, y(θ)), we make the following assumptions, unless otherwise stated; all its partial derivatives used later exist and satisfy the following:

()

Many numerical methods have been proposed for the numerical solution of (1).

In this paper, we are concerned with two-step Runge-Kutta (TSRK) methods of the form

()

where

, h = τ/m is a stepsize, m is an arbitrarily given positive integer, and 0 ≤ θ ≤ 1. The above methods are studied in [17]. Now we consider the adaptation of the two-step Runge-Kutta method to (1):

()

In particular, y₀ = φ(0), y_n is the numerical approximation at t_n = nh to the analytic solution y(t_n), the argument

denotes an approximation to y(t_n + c_jh − τ), and the argument

denotes an approximation to

which are obtained by a convergent compound quadrature (CQ) formula:

()

using values

with n ≤ q, t_n−q + c_jh ≤ 0.

The class of Runge-Kutta methods with CQ formula has been applied to delay-integro-differential equations by many authors (c.f. [18, 19]). For the CQ formula (9), we usually adopt the repeated trapezoidal rule, the repeated Simpson’s rule, or the repeated Newton-cotes rule, and so forth, denote . It should be pointed out that the adopted quadrature formula (9) is only a class of quadrature formula for , there also exist some other types of quadrature formula, such as Pouzet quadrature (PQ) formula and the quadrature formula based on Laguerre-Radau interpolations [20, 21]. It is the aim of our future research to investigate the adaptation of PQ formula and the quadrature formula based on Laguerre-Radau interpolations to VDIDEs.

3. The Nonlinear Stability Analysis

In this section, we will investigate the stability of the two-step Runge-Kutta methods for VDIDEs. In order to consider the stability property, we also need to consider the perturbed problem of (1):

()

where ψ : [−τ, 0] → C^N is a given continuous function. The unique exact solution of the problem (10) is denoted as z(t).

Applying the two-step Runge-Kutta method (7a)–(7c) to (10) leads to

()

where z_n and

denote approximations to z(t_n) and z(t_n + c_ih), respectively; the argument

denotes an approximation to

which are obtained by a convergent compound quadrature (CQ) formula:

()

and

denotes an approximation to z(t_n + c_jh − τ), and z_n = ψ(t_n) for n = 0,

()

3.1. Some Concepts

For the stability analysis, we need the compound quadrature formula (9) that satisfies the following condition:

()

where

is a positive constant.

Let

()

It follows from (8a)–(8c) and (11a)–(11c) that

()

Now we will write the s-stage TSRK methods (7a)–(7c) as a general linear method.

Let

be the internal stages and

the external vectors and

. Then we have a 2(s + 1)-stage partitioned general linear method:

()

where

, i = s + 1, s + 2, ⋯, 2s, j = 1,2, ⋯, s,

, i, j = s + 1, s + 2, ⋯, 2s,

, i, j = 1,2, ⋯, s,

, i = 1,2, ⋯, s, j = s + 1, s + 2, ⋯, 2s,

, i = s + 1, s + 2, ⋯, 2s, j = 1,2, ⋯, s,

, i, j = s + 1, s + 2, ⋯, 2s,

, i, j = 1,2, ⋯, s,

, i = 1,2, ⋯, s, j = s + 1, s + 2, ⋯, 2s,

, i = s + 1, s + 2, ⋯, 2s, j = 1,2, ⋯, s,

, i, j = s + 1, s + 2, ⋯, 2s,

, i, j = 1,2, ⋯, s,

, i = 1,2, ⋯, s, j = s + 1, s + 2, ⋯, 2s,

, i = s + 1, s + 2, ⋯, 2s, j = 1,2, ⋯, s,

, i, j = s + 1, s + 2, ⋯, 2s, and A = (a_ij), e = (1,1, …1), b = (b₁, b₂, …, b_s),

We can identify the coefficient matrices

()

Definition 1 (see [22].)Let k, l be real constants, a TSRK method is said to be (k, l) algebraically stable if there exists a diagonal matrix D = diag(d₁, d₂, …, d_2s) and a diagonal nonnegative matrix G such that M = (m_ij) is nonnegative, where

()

In particular, a (1,0)-algebraically stable method is called algebraically stable.

Definition 2. The TSRK method (7a)–(7c) is called asymptotically stable for (1) with (2)–(4) if lim_n→∞∥w_n∥ = 0.

3.2. Numerical Stability of the Methods

Numerical stability is an important feature of an effective numerical method. An unstable numerical method may be consistent of high order, yet arbitrarily small perturbations will eventually cause large deviations from the true solution. In this section, we will focus on the asymptotic stability of the TSRK method.

Theorem 3. Assume that the TSRK method (7a)–(7c) is (k, l)-algebraically stable with 0 < k ≤ 1, suppose that the quadrature formula (9) satisfies the condition (14) and the conditions (2)–(4) hold, then, method (17a) and (17b) satisfies the following:

()

when the following condition holds:

()

where C depends only on the method, the parameters α, β, σ, γ, η, and τ.

Proof. It follows from a fairly straightforward (but tedious) computation and (k, l) algebraically stability that (compare also [22, 23])

()

where

()

By means of (k, l) algebraical stability of the method, we have the following:

()

It follows from (2)–(4) that

()

Substituting (25) into (24), using (14) we get the following:

()

By induction, we get the following:

()

Hence, ∥μ_n+1∥ ≤ C max_{t∈[−τ,0]}∥φ(t) − ψ(t)∥, where

The proof of Theorem 3 is completed.

Theorem 4. Assume that a TSRK method (7a)–(7c) is (k, l)-algebraically stable with 0 < k < 1, then the TSRK method (7a)–(7c) with (9), (12) and (14) is asymptotically stable for the problem (1) with (2)–(4), when the following condition holds:

()

Proof. Let

()

Then when

, we have

and

The application of Theorem 3 yields the following:

()

By induction, we get the following:

()

The inequality together with the knowledge

leads to the following:

()

Because

, we can get from (33) that

()

The proof of the theorem is completed.

4. The Convergence of TSRK Method for NDDEs

4.1. Some Concepts

In order to study the convergence of the method, we define the following:

()

Thus, process (8a)–(8c) can be written in the more compact form:

()

Definition 5. Method (7a)–(7c) with an approximation procedure (9) is said to be D convergent of order p if the global error satisfies a bound of the form

()

where H(t) and Y(t) are defined by

()

where ρ₁(t) and h₀ depend on M_i, α, β, γ, σ, and τ.

Definition 6. TSRK Method (7a)–(7c) is said to be diagonally stable if there exist a 2s × 2s diagonal matrix Q > 0 such that the matrix is positive definite.

Remark 7. The concepts of algebraic stability and diagonal stability of TSRK method are the generalizations of corresponding concepts of Runge-Kutta methods. Although it is difficult to examine these conditions, many results have been found, especially, there exist algebraically stable and diagonally stable multistep formulas of arbitrarily high order (cf. [24]).

Definition 8. TSRK Method (7a)–(7c) is said to have generalized stage order p if p is the largest integer which possesses the following properties.

For any given problem (1) and , there exists an abstract function H^h(t),

()

such that

()

where the maximum stepsize

and the constant p₁ depend only on the method and the bounds M_i, Δ^h(t) and δ^h(t), they are defined by the following equations:

()

The function Y^′(t) is defined by the following:

()

Particularly, when H(t) = H^h(t), generalized stage order is called stage order.

4.2. D-Convergence and Proofs

In this section, we focus on the error analysis of TSRK method for (1). For the sake of simplicity, we always assume that all constants h_i, γ_i, d_i, and L_i are dependent on the method, the bounds M_i, N_i, the parameters α, β, γ, σ, and τ.

First, we give a preliminary result which will later be used several times. To simplify, we denote

for

, and ζ, ϖ ∈ C^2N for ζ⁽ⁿ⁺¹⁾, ϖ⁽ⁿ⁺¹⁾, where ϖ⁽ⁿ⁺¹⁾ = (z⁽ⁿ⁺¹⁾, z⁽ⁿ⁾). Define

and

by the following:

()

Theorem 9. Suppose method (7a)–(7c) is diagonally stable, then there exist constants h₁, p₂, and p₃ such that

()

Proof. Since the method (7a)–(7c) is diagonally stable, there exists a positive definite diagonal matrix Q such that the matrix is positive definite. Therefore, the matrix C₁₁ is obviously nonsingular and there exists a l > 0 depends only on the method such that the matrix

()

is also positive definite.

Define

()

then

()

Using (2)–(4), (44), (46a), and (46b), we have for hα ≤ l,

()

where λ_l is the minimum eigenvalue of E_l. Therefore,

()

where

()

From (43a), (49a), and (49b), it follows that

()

where

, which completes the proof of Theorem 9.

Consider the compact form of (11a)–(11c):

()

where

()

Theorem 10. Suppose the method (7a)–(7c) is algebraically stable for the matrices G and D, then for (36a), (36b), (51a), and (51b), one has the following:

()

where p₄ = ∥D∥ · max{(2α + β + σ), β, σ}, ∥·∥ is a norm on C^2sN defined by the following:

()

Proof. Define u⁽ⁿ⁾ = ζ⁽ⁿ⁾ − ϖ⁽ⁿ⁾, we get from (45a)–(45d) that

()

With algebraic stability, the matrix

()

is nonnegative definite. As in [25], we have

()

Using (2)–(4), we further obtain the following:

()

which gives (53). The proof is completed.

In the following, we assume that the method (7a)–(7c) has generalized stage order p; that is, there exists a function H^h(t) such that (40) holds. For any >0, we define

and

by the following:

()

where

()

Theorem 11. Suppose the method (7a)–(7c) is diagonally stable and its generalized stage order is p, then there exist constants p₅ and h₂ such that

()

where p₅, C₁, C₂, and C₃ depend on p₂, s, d₁, h₁, and ∥C₁₂∥.

Proof. A combination of (36a) and (41a) leads to the following:

()

It follows from Theorem 9 that

()

A combination of (4) and (9) gives the following:

()

where

and ν depend only on the compound quadrature (CQ) formula (9), which on substitution into (63) gives the following:

()

Therefore, there exist p₅ and h₂ such that (61) holds. The proof of Theorem 11 is completed.

Theorem 12. Suppose method (7a)–(7c) is algebraically stable and diagonally stable and its generalized stage order is p. Then the method with quadrature formula (9) is D-convergent of order at least min{p, ν}.

Proof. A combination of (36b), (59b), and (53) leads to the following:

()

Using Theorem 9, we have the following:

()

which on substitution into (66) gives the following:

()

where λ₂ is the minimum characteristic value of G. On the other hand,

()

In view of (41a)–(41c) and (59a) and (59b), the application of Theorem 9 leads to the following:

()

which gives

()

where λ₁ denotes the maximum eigenvalue of the matrix G. A combination of (40) and (66)–(71) leads to the following:

()

where

()

Considering Theorem 11, we further obtain the following:

()

Using discrete Bellman inequality, we have the following:

()

where h ∈ (0, h₀], and

Considering ∥H(t) − H^h(t_n)∥ ≤ p₀h^p, we obtain the following:

()

Considering (75) and (76), we can easily conclude that method (7a)–(7c) with quadrature formula (9) is D-convergent of order at least >min{p, ν}. The proof is completed.

5. Numerical Experiments

Consider the following nonlinear Volterra delay integro-differential equations:

()

and its perturbed problem

()

One may check that this system has the solution y(t) = exp(cost) and a = −4, β = 1/2, σ = 1/2, γ = 1. With Theorem 9, we conclude that system (77) satisfies stability and convergence properties.

Apply the two-step Runge-Kutta method induced by the GL method in [12]

()

to (77) and (78),

is computed by the compound Simpson rule with an even integer m ≥ 4 formula:

()

Using the condition (28), we know this method is stable; the convergence order is shown in Table 1.

For Figures 1 and 2, it is obvious that the corresponding method for VDIDEs is stable and convergent, and the convergent order is min{4,4}.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The numerical solution of (79a) and (79b) for (77) with h = 0.1.

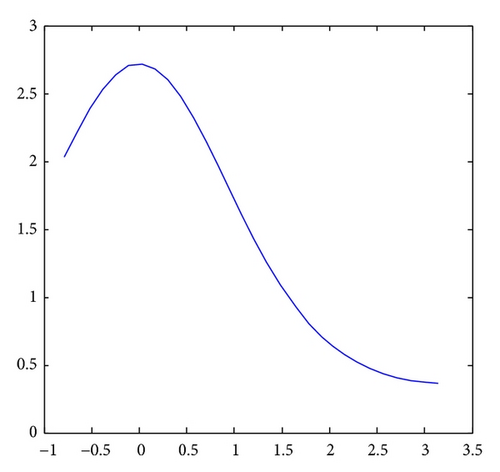
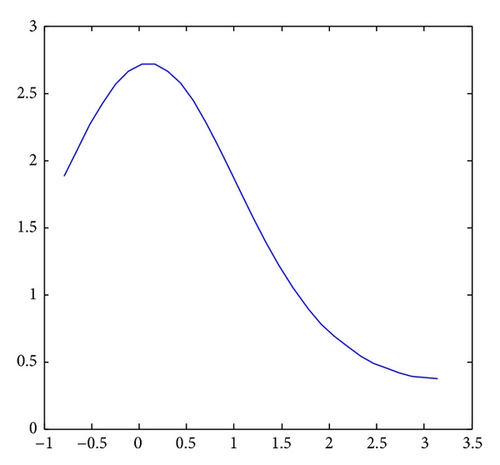
6. Conclusions

This paper is devoted to the stability and convergence analysis of the two-step Runge-Kutta (TSRK) methods with compound quadrature formula for the numerical solution for a nonlinear Volterra delay integro-differential equations. Nonlinear stability and D-convergence are introduced and proved.

We believe that the results presented in this paper can be extended to other general DIDEs and NDIDEs. However, it is difficult to extend the results presented in this paper to more general delay differential equations; the discussion will be discussed later.

Acknowledgments

This work was supported by the Education Foundation of Heilongjiang Province of China (12523039) and the Doctor Foundation of Heilongjiang Institute of Technology (2012BJ27).

References

1 Shakourifar M. and Dehghan M., On the numerical solution of nonlinear systems of Volterra integro-differential equations with delay arguments, Computing. (2008) 82, no. 4, 241–260, https://doi.org/10.1007/s00607-008-0009-4, MR2438770.
10.1007/s00607-008-0009-4
Web of Science® Google Scholar
2 Li S. F., B-convergence properties of multistep Runge-Kutta methods, Mathematics of Computation. (1994) 62, no. 206, 565–575, https://doi.org/10.2307/2153523, MR1201071.
10.2307/2153523
Web of Science® Google Scholar
3 Burrage K. and Butcher J. C., Nonlinear stability of a general class of differential equation methods, BIT Numerical Mathematics. (1980) 20, no. 2, 185–203, https://doi.org/10.1007/BF01933191, MR583033.
10.1007/BF01933191
Google Scholar
4 Huang C., Li S., Fu H., and Chen G., Nonlinear stability of general linear methods for delay differential equations, BIT Numerical Mathematics. (2002) 42, no. 2, 380–392, https://doi.org/10.1023/A:1021955126558, MR1912593.
10.1023/A:1021955126558
Web of Science® Google Scholar
5 Burrage K., High order algebraically stable multistep Runge-Kutta methods, SIAM Journal on Numerical Analysis. (1987) 24, no. 1, 106–115, https://doi.org/10.1137/0724009, MR874738.
10.1137/0724009
Web of Science® Google Scholar
6 Li S., Stability and B-convergence properties of multistep Runge-Kutta methods, Mathematics of Computation. (2000) 69, no. 232, 1481–1504, https://doi.org/10.1090/S0025-5718-99-01159-X, MR1659839.
10.1090/S0025-5718-99-01159-X
Web of Science® Google Scholar
7 Linz P., Analytical and Numerical Methods for Volterra Equations, 1985, Society for Industrial and Applied Mathematics, Philadelphia, Pa, USA, SIAM Studies in Applied Mathematics, https://doi.org/10.1137/1.9781611970852, MR796318.
10.1137/1.9781611970852
Google Scholar
8 Li S. F., Nonlinear stability of general linear methods, Journal of Computational Mathematics. (1991) 9, no. 2, 97–104, MR1150169.
Google Scholar
9 Baker C. T. H. and Ford N. J., Convergence of linear multistep methods for a class of delay-integro-differential equations, International series of Numerical Mathematics. (1988) 86, 47–59, MR1022945.
10.1007/978-3-0348-6303-2_4
Google Scholar
10 Baker C. T. H. and Ford N. J., Asymptotic error expansions for linear multistep methods for a class of delay integro-differential equations, Bulletin de la Société Mathématique de Grèce. (1990) 31, 5–18, MR1108903.
Google Scholar
11 Baker C. T. H. and Ford N. J., Stability properties of a scheme for the approximate solution of a delay-integro-differential equation, Applied Numerical Mathematics. (1992) 9, no. 3–5, 357–370, https://doi.org/10.1016/0168-9274(92)90027-B, MR1158494.
10.1016/0168-9274(92)90027-B
Web of Science® Google Scholar
12 Zhang C. and Vandewalle S., Stability analysis of Runge-Kutta methods for nonlinear Volterra delay-integro-differential equations, IMA Journal of Numerical Analysis. (2004) 24, no. 2, 193–214, https://doi.org/10.1093/imanum/24.2.193, MR2046174.
10.1093/imanum/24.2.193
Web of Science® Google Scholar
13 De la Sen M. and Luo N., On the uniform exponential stability of a wide class of linear time-delay systems, Journal of Mathematical Analysis and Applications. (2004) 289, no. 2, 456–476, https://doi.org/10.1016/j.jmaa.2003.08.048, MR2026918.
10.1016/j.jmaa.2003.08.048
Web of Science® Google Scholar
14 De la Sen M., Stability of impulsive time-varying systems and compactness of the operators mapping the input space into the state and output spaces, Journal of Mathematical Analysis and Applications. (2006) 321, no. 2, 621–650, https://doi.org/10.1016/j.jmaa.2005.08.038, MR2241144.
10.1016/j.jmaa.2005.08.038
Web of Science® Google Scholar
15 Baker C. T. H. and Tang A., Stability analysis of continuous implicit Runge-Kutta methods for Volterra integro-differential systems with unbounded delays, Applied Numerical Mathematics. (1997) 24, no. 2-3, 153–173, https://doi.org/10.1016/S0168-9274(97)00018-4, MR1464721.
10.1016/S0168-9274(97)00018-4
Web of Science® Google Scholar
16 Zhang C. and Vandewalle S., General linear methods for Volterra integro-differential equations with memory, SIAM Journal on Scientific Computing. (2006) 27, no. 6, 2010–2031, https://doi.org/10.1137/040607058, MR2211437.
10.1137/040607058
Web of Science® Google Scholar
17 Kuang J. X., Xiang J. X., and Tian H. J., The asymptotic stability of one-parameter methods for neutral differential equations, BIT Numerical Mathematics. (1994) 34, no. 3, 400–408, https://doi.org/10.1007/BF01935649, MR1429940.
10.1007/BF01935649
Web of Science® Google Scholar
18 Hale J. K. and Verduyn Lunel S. M., Introduction to Functional-Differential Equations, 1993, Springer, Berlin, Germany, MR1243878.
10.1007/978-1-4612-4342-7
Google Scholar
19 Chengjian Z. and Shuzi Z., Nonlinear stability and D-convergence of Runge-Kutta methods for delay differential equations, Journal of Computational and Applied Mathematics. (1997) 85, no. 2, 225–237, https://doi.org/10.1016/S0377-0427(97)00118-0, MR1482166.
10.1016/S0377-0427(97)00118-0
Web of Science® Google Scholar
20 Guo B.-Y., Wang Z.-Q., Tian H.-J., and Wang L.-L., Integration processes of ordinary differential equations based on Laguerre-Radau interpolations, Mathematics of Computation. (2008) 77, no. 261, 181–199, https://doi.org/10.1090/S0025-5718-07-02035-2, MR2353948.
10.1090/S0025-5718-07-02035-2
Web of Science® Google Scholar
21 Guo B.-Y. and Zhang X.-Y., A new generalized Laguerre spectral approximation and its applications, Journal of Computational and Applied Mathematics. (2005) 181, no. 2, 342–363, https://doi.org/10.1016/j.cam.2004.12.008, MR2146844.
10.1016/j.cam.2004.12.008
Web of Science® Google Scholar
22 Frank R., Schneid J., and Ueberhuber C. W., The concept of B-convergence, SIAM Journal on Numerical Analysis. (1981) 18, no. 5, 753–780, https://doi.org/10.1137/0718051, MR629662.
10.1137/0718051
Web of Science® Google Scholar
23 Koto T., Stability of Runge-Kutta methods for delay integro-differential equations, Journal of Computational and Applied Mathematics. (2002) 145, no. 2, 483–492, https://doi.org/10.1016/S0377-0427(01)00596-9, MR1917284.
10.1016/S0377-0427(01)00596-9
Web of Science® Google Scholar
24 Huang C. M., Algebraic stability of hybrid methods, Chinese Journal of Numerical Mathematics and Applications. (1995) 17, 67–74.
Google Scholar
25 Li S. F., Theory of Computational Methods for Stiff Differential Equations, 1997, Hunan Science and Technology Publisher, Changsha, China.
Google Scholar

All articles

Nonlinear Stability and Convergence of Two-Step Runge-Kutta Methods for Volterra Delay Integro-Differential Equations

Abstract

1. Introduction

2. A Class of VDIDES and the Two-Step Runge-Kutta Methods

3. The Nonlinear Stability Analysis

3.1. Some Concepts

3.2. Numerical Stability of the Methods

4. The Convergence of TSRK Method for NDDEs

4.1. Some Concepts

4.2. D-Convergence and Proofs

5. Numerical Experiments

6. Conclusions

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Nonlinear Stability and Convergence of Two-Step Runge-Kutta Methods for Volterra Delay Integro-Differential Equations

Abstract

1. Introduction

2. A Class of VDIDES and the Two-Step Runge-Kutta Methods

3. The Nonlinear Stability Analysis

3.1. Some Concepts

3.2. Numerical Stability of the Methods

4. The Convergence of TSRK Method for NDDEs

4.1. Some Concepts

4.2. D-Convergence and Proofs

5. Numerical Experiments

6. Conclusions

Acknowledgments

References

Figures

References

Related

Information