Recursive Neural Networks Based on PSO for Image Parsing
Abstract
This paper presents an image parsing algorithm which is based on Particle Swarm Optimization (PSO) and Recursive Neural Networks (RNNs). State-of-the-art method such as traditional RNN-based parsing strategy uses L-BFGS over the complete data for learning the parameters. However, this could cause problems due to the nondifferentiable objective function. In order to solve this problem, the PSO algorithm has been employed to tune the weights of RNN for minimizing the objective. Experimental results obtained on the Stanford background dataset show that our PSO-based training algorithm outperforms traditional RNN, Pixel CRF, region-based energy, simultaneous MRF, and superpixel MRF.
1. Introduction
Image parsing is an important step towards understanding an image, which is to perform a full-scene labeling. The task of image parsing consists in labeling every pixel in the image with the category of the object it belongs to. After a perfect image parsing, every region and every object are delineated and tagged [1]. Image parsing is frequently used in a wide variety of tasks including parsing scene [2, 3], aerial image [4], and facade [5].
During the past decade, the image parsing technique has undergone rapid development. Some methods for this task such as [6] rely on a global descriptor which can do very well for classifying scenes into broad categories. However, these approaches fail to gain a deeper understanding of the objects in the scene. Many other methods rely on CRFs [7], MRFs [8], or other types of graphical models [9, 10] to ensure the consistency of the labeling and to account for context. Also, there are many approaches for image annotation and semantic segmentation of objects into regions [11]. Note that most of the graphical-based methods rely on a presegmentation into superpixels or other segment candidates and extract features and categories from individual segments and from various combinations of neighboring segments. The graphical model inference pulls out the most consistent set of segments which covers the image [1]. Recently, these ideas have been combined to provide more detailed scene understanding [12–15].
It is well known that many graphical methods are based on neural networks. The main reason is that neural networks have promising potential for tasks of classification, associative memory, parallel computation, and solving optimization problems [16]. In 2011, Socher et al. proposed a RNN-based parsing algorithm that aggregates segments in a greedy strategy using a trained scoring function [17]. It recursively merges pairs of segments into supersegments in a semantically and structurally coherent way. The main contribution of the approach is that the feature vector of the combination of two segments is computed from the feature vectors of the individual segments through a trainable function. Experimental results on Stanford background dataset revealed that RNN-based method outperforms state-of-the-art approaches in segmentation, annotation, and scene classification. That being said, it is worth noting that the objective function is nondifferentiable due to the hinge loss. This could cause problems since one of the principles of L-BFGS, which is employed as the training algorithm in RNN, is that the objective should be differentiable.
Since Particle Swarm Optimization (PSO) [18] has proven to be an efficient and powerful problem-solving strategy, we use a novel nonlinear PSO [19] to tune the weights of RNN. The main idea is to use particle swarm for searching good combination of weights to minimize the objective function. The experimental results show that the proposed algorithm has better performance than traditional RNN on Stanford background dataset.
The rest of the paper is organized as follows: Section 2 provides a brief description of the RNN-based image parsing algorithm. Section 3 describes how PSO and the proposed algorithm work. Section 4 presents the dataset and the experimental results. Section 5 draws conclusions.
2. Image Parsing Based on Recursive Neural Networks
The main idea behind recursive neural networks for image parsing lies in that images are oversegmented into small regions and each segment has a vision feature. These features are then mapped into a “semantic” space using a recursive neural network. Figure 1 outlines the approach for RNN-based image parsing method. Note that the RNN computes (i) a score that is higher when neighboring regions should be merged into a larger region, (ii) a new semantic feature representation for this larger region, and (iii) its class label. After regions with the same object label are merged, neighboring objects are merged to form the full scene image. These merging decisions implicitly define a tree structure in which each node has associated with the RNN outputs (i)–(iii), and higher nodes represent increasingly larger elements of the image. Details of the algorithm are given from Sections 2.1 to 2.3.
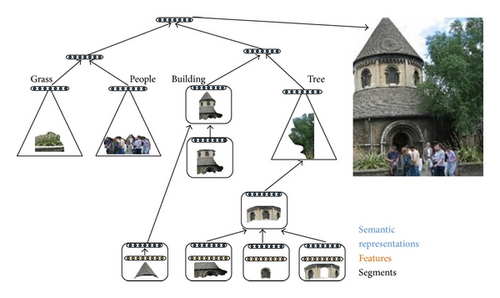
2.1. Input Representation of Scene Images
Firstly, an image x is oversegmented into superpixels (also called segments) using the algorithm from [20]. Secondly, for each segment, compute 119 features via [10]. These features include color and texture features, boosted pixel classifier scores (trained on the labeled training data), and appearance and shape features. Thirdly, a simple neural network layer has been used to map these features into the “semantic” n-dimensional space in which the RNN operates, given as follows.

2.2. Greedy Structure Predicting
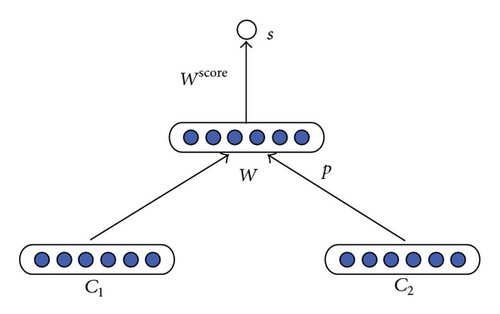
2.3. Category Classifiers in the Tree
3. Nonlinear Particle Swarm Optimization for Training FNN
As for traditional RNN-based method, the objective J of (5) is not differentiable due to the hinge loss. For training RNN, Socher used L-BFGS over the complete training data to minimize the objective, where the iteration of the swarm relates to the update of the parameters of RNN. That being said, it is worth noting that the basic principle of L-BFGS is that the objective function should be differentiable. Since the objective function for RNN is nondifferentiable, L-BFGS could cause problems for computing the weights of RNN. To solve this problem, a novel nonlinear PSO (NPSO) has been used to tune the parameters of RNN.
3.1. Nonlinear Particle Swarm Optimization
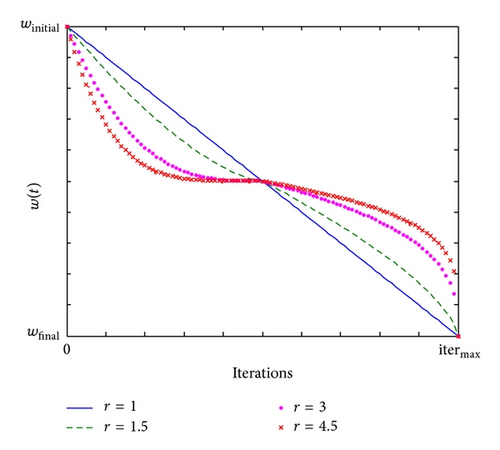
Note that a suitable value for the inertia weight provides a balance between the global and local exploration abilities of the swarm. Based on the concept of decrease strategy, our nonlinear inertia weight strategy [19] chooses a lower value of w during the early iterations and maintains higher value of w than linear model [21]. This strategy enables particles to search the solution space more aggressively to look for “better areas”, thus will avoid local optimum effectively.
Figure 4 illustrates the variations of nonlinear inertia weight for different values of r. Note that r = 1 is equal to the linear model. In [19], we showed that a choice of r within [2-3] is normally satisfactory.
3.2. Encoding Strategy and Fitness Evaluation
3.3. Summary of PSO-Based Training Algorithm
-
Input includes a set of labeled images, the size of the hidden layer n, the value of penalization term for incorrect parsing decisions κ, the regularization parameter λ, the population of particles m, the values of nonlinear parameter r and the number of iterations itermax.
-
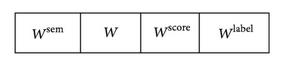
Output includes the set of model parameters θ = (Wsem, W, Wscore, and Wlabel), each with respect to weights of a recursive neural network.
- (1)
Randomly initialize m particles and randomize the positions and velocities for entire population. Record the global best location pg of the population and the local best locations pi of the ith particle according to (9), where i = 1,2, …, m.
- (2)
For each iteration, evaluate the fitness value of the ith particle through (9). If (f(xi)) < (f(pi)), set pi = xi as the so far best position of the ith particle. If (f(xi)) < (f(pg)), set pg = xi as the so far best position of the population.
- (3)
Calculate the inertia weight through (7). Update the position and velocity of particles according to (6).
- (4)
Repeat Step 2 and Step 3 until maximum number of generation.
- (5)
Compute the weights of RNN according to the best particle.
4. Experimental Results and Discussion
4.1. Description of the Experiments
In this section, PSO-based RNN method is compared with traditional RNN [17], pixel CRF [10], region-based energy [10], simultaneous MRF [8], and superpixel MRF [8], by using images from Stanford background dataset. All the experiments have been conducted on a computer with Intel sixteen-core processor 2.67 GHz processor and 32 GB RAM.
As for RNN, Socher recommends that the size of the hidden layer n = 100, the penalization term for incorrect parsing decisions κ = 0.05, and the regularization parameter λ = 0.001. As for the particle swarm optimization, we set the population of particles m = 100, the number of iterations itermax = 500, c1 = c2 = 2, winitial = 0.95, wfinal = 0.4, and r = 2.5.
4.2. Scene Annotation
The first experiment aims at evaluating the accuracy of scene annotation on the Stanford background dataset. Like [17], we run fivefold cross-validation and report pixel level accuracy in Table 1. Note that the traditional RNN model influences the leaf embeddings through backpropagation, while we use PSO to tune the weights of RNN. As for traditional RNN model, we label the superpixels by their most likely class based on the multinomial distribution from the softmax layer at the leaf nodes. One can see that in Table 1, our approach outperforms previous methods that report results on this data, which means that the PSO-based RNN constructs a promising strategy for scene annotation. Some typical parsing results are illustrated in Figure 5.
| Method and semantic pixel accuracy in % |
|---|
| Pixel CRF, Gould et al. (2009) 74.3 |
| Log. Regr. on superpixel features 75.9 |
| Region-based energy, Gould et al. (2009) 76.4 |
| Local labeling, Tighe and Lazebnik (2010) 76.9 |
| Superpixel MRF, Tighe and Lazebnik (2010) 77.5 |
| Simultaneous MRF, Tighe and Lazebnik (2010) 77.5 |
| Traditional RNN, Socher and Fei-Fei (2011) 78.1 |
| PSO-based RNN (our method) 78.3 |

4.3. Scene Classification
As described in [17], the Stanford background dataset can be roughly categorized into three scene types: city, countryside, and sea side. Therefore, like traditional RNN, we trained SVM that using the average over all nodes’ activations in the tree as features. That means the entire parse tree and the learned feature representations of the RNN are taken into account. As a result, the accuracy has been promoted to 88.4%, which is better than traditional RNN (88.1%) and Gist descriptors (84%) [6]. If only the top node of the scene parse tree is considered, we will get 72%. The results reveal that it does lose some information that is captured by averaging all tree nodes.
5. Conclusions
In this paper, we have proposed an image parsing algorithm that is based on PSO and Recursive Neural Networks (RNNs). The algorithm is an incremental version of RNN. The basic idea is to solve the problem of nondifferentiable objective function of traditional training algorithm such as L-BFGS. Hence, PSO has been employed as an optimization tool to tune the weights of RNN. The experimental results reveal that the proposed algorithm has better performance than state-of-the-art methods on Stanford background dataset. That being said, the iteration of swarms dramatically increases the runtime of the training process. Our future work may focus on reducing the time complexity of the algorithm.
Acknowledgments
This work was supported by the National Nature Science Foundation of China (No. 61202143, No. 61103052, and No. 11101187); Major Project of Industry University of Fujian Province (2011H6020); Doctoral Program Foundation of Institutions of Higher Education of China (No. 20090121110032); Shenzhen Science and Technology Research Foundation (Nos. JC200903180630A, ZYB200907110169A); The Natural Science Foundation of Xiamen City, China (3502Z20123022).




