Abstract and Applied Analysis
Volume 2013, Issue 1 612342
Research Article
Open Access

Third-Order Leader-Following Consensus in a Nonlinear Multiagent Network via Impulsive Control

Xiaomei Li, 

Xiaomei Li

School of Mathematics and Computing Science, Guilin University of Electronic Technology, Guilin 541004, China

Search for more papers by this author
Zhongjun Ma, 

Corresponding Author

Zhongjun Ma

School of Mathematics and Computing Science, Guilin University of Electronic Technology, Guilin 541004, China

Search for more papers by this author
Chunhai Li, 

Chunhai Li

School of Mathematics and Computing Science, Guilin University of Electronic Technology, Guilin 541004, China

Search for more papers by this author
Jinde Cao, 

Jinde Cao

Department of Mathematics, Southeast University, Nanjing 210096, China seu.edu.cn

Search for more papers by this author
First published: 26 September 2013
https://doi.org/10.1155/2013/612342
Academic Editor: Qiankun Song

Abstract

Many facts indicate that the impulsive control method is a finer method, which is simple, efficient, and low in cost, for achieving consensus. In this paper, based on graph theory, Lyapunov stability theory, and matrix theory, a novel impulsive control protocol is given to realize the consensus of the multiagent network. Numerical simulations are performed to verify the theoretical results.

1. Introduction

In the past few years, consensus of multiagent networks has been intensively studied in many fields, such as biological, social, mathematical, and physical sciences ones [1–5]. Generally speaking, consensus refers to designing a system algorithm or protocol such that all agents asymptotically reach an agreement on their states. In particular, leader-following consensus means that there exists a virtual leader which specifies an objective for all agents to follow. Recently, some first-order and second-order leader-following consensus problems were discussed by lots of researchers [6–10], and then some novel system algorithms were given via some different control methods, such as pinning control, delay coupling control, adaptive control, and impulsive control [9–14]. In addition, Qin et al. considered consensus in the second-order multiagent system with communication delay in [15, 16]. Particularly, some multiagent networks cannot be controlled continuously. At this time, the impulsive control becomes a more desirable alternative. The impulsive control is low in cost and then has been widely applied in many fields, such as information science, system control, life science, communication security, and space techniques [17–19]. In the above senses, the impulsive control is very effective for achieving consensus of a multiagent network.

In some real networks, the connections between part nodes are sometimes a failure, and then the network topology may dynamically change over time. Therefore, it is indispensable to consider the case that the network topology is switching. As much as we know, most of the relevant studies focus on second-order consensus for multiagent networks [11, 12]. When the agent states are influenced by speeds, positions, and accelerations, it is necessary and significative to research the third-order consensus problem of a multiagent network with switching topology. At present, just few works considered the third-order consensus problem. In [20], adaptive third-order leader-following consensus of a nonlinear multiagent network with perturbations was addressed, without using the impulsive control method. In [11], impulsive consensus problem of second-order multiagent network with switching topologies was investigated, without considering its own dynamics. In this paper, we consider the third-order consensus problem in a multiagent network with the aforementioned four characters, that is, leader-following, own dynamics, switching topology, and impulsive control. By using the graph theory, Lyapunov stability theory, and matrix theory, some sufficient conditions are obtained to realize the third-order leader-following consensus.

The rest of this paper is designed as follows. Some necessary preliminaries are stated in Section 2. The consensus of a multiagent network is discussed in Section 3. Numerical examples are given to verify the theoretical results in Section 4. Finally, in Section 5, conclusions are presented.

2. Preliminaries

2.1. Multiagent Network

Information exchange among agents can be modeled by an interaction graph. Let G = {V, E, A} be a weighted diagraph with a node set V = {1, …, N}, an edge set E⊆V × V, and a weight adjacency matrix A = (aij) N×N. A directed edge denoted by (i, j) means that j has access to node i; that is, node j can receive information from node i. The elements of matrix A are defined such that aij > 0 for (j, i) ∈ E, while aij = 0 for (j, i) ∉ E. Let aii = 0 for i ∈ V. The set ℵi = {j ∈ V∣(j, i) ∈ E} is used as the neighbor set of node i. When the communication topology is switching, the neighbor set is time-varying, and then ℵi(t) = {j ∈ V : aij(t) > 0}. Let
()
The out-degree of node i is defined by . If the degree matrix of digraph G is D = diag (d1, …, dN), then the Laplacian matrix of digraph G is L = D − A.

A directed path from node i to node j in the directed graph G is a sequence of edges (i, j1), (j1, j2), …, (jl, j) with distinct nodes jk, k = 1, …, l. A digraph G has a directed spanning tree if there exists at least one node called root which has a directed path to all the other nodes.

For a leader-follower multiagent network, suppose that the leader (labeled by 0) is denoted by node 0, and the followers are denoted by the nodes 1,2, …, N. The graph is consisting of the leader and the followers with communication topology. The connection weight between the ith follower and the leader is represented by bi, i ∈ V. If the ith follower is connected to the leader, then bi > 0; otherwise, bi = 0. Let B = diag {b1, b2, …, bN}.

Following, we address the multiagent network with switching topology. The set is used as a set of the graphs with all possible topology, which includes all possible graphs (involving N agents and a leader). We define a switching signal τ : [0, +∞) → P = {1,2, …, m}, which determines the topology structure that corresponds to the network. When the topology is switching, the Laplacian matrix L and the matrix B are also switching, which are denoted by Lτ(t) and Bτ(t).

The following assumptions are needed to derive our main results.

Assumption 1 (see [21].)Assume that there exists a constant γ > 0, such that the vector-valued function f satisfies the condition

()
for any x, y, z, u, v, w ∈ Rn.

2.2. Impulsive Control System

Impulsive control systems can be classified into three types based on the characteristics of plants and control laws [22].

A type-I impulsive control system [22] is given by
()
where X and Y are the state variable and the output, respectively. U(k, Y) is the impulsive control law. In this kind of system, the control input is implemented by the “sudden jumps" of some state variables.

Definition 2 (see [22].)For t ≠ τk(X), we define the time derivative of the function V(t, X) with respect to system (3) as

()

Type-II and type-III impulsive control systems and more theoretical results are present in [22].

In this paper, a type-I impulsive control system is considered.

3. Main Results

Consider that a nonlinear multiagent network consists of N agents with third-order dynamics:
()
where , vi = (vi1, …, vin) T ∈ Rn, and ui = (ui1, …, uin) T ∈ Rn are the position, velocity, and acceleration states of the ith agent, respectively, and f = (f1, …, fn) T ∈ Rn is a nonlinear vector-valued continuous function used to describe the self-dynamics of the ith agent.
The virtual leader of the multiagent network (5) is an isolated agent described by
()
where x0 ∈ Rn, v0 ∈ Rn, and u0 ∈ Rn are the position, velocity, and acceleration of the virtual leader, respectively.
For t ∈ (tk−1, tk), the state variables xi(t), vi(t), u(t) of the system (5) do dynamically change with ordinary differential equations. And at the moment tk, if the xi(t), vi(t), u(t) supervise the impulsive control, then it can result in the jump. Based on the above senses and the impulsive controller of [11] and applying impulsive control to (5), we have the following consensus scheme for the multiagent system:
()
where Δxi(tk), Δvi(tk), Δui(tk) are the jump of the position, velocity, and acceleration of the ith follower agent at the moment tk, respectively, , , , , , , Ck ∈ Rn×n is the impulsive controller gain at the moment tk, the moments of impulsive satisfy 0 ≤ t0 < t1 < t2 < ⋯<tk < tk+1 < ⋯, and lim k→+∞ tk = +∞, Δtk = tk − tk−1 ≤ ρ < +∞ is the impulsive interval, where k = 1,2, ….
Let , , , , , , ; then the error system with (6) and (7) can be written as
()
where
()
Lτ(k) and Bτ(k) are associated with the switching interconnection graph at time tk, τ(k) ∈ P.

Definition 3. Denote exi(t) = ∥xi(t) − x0(t)∥, evi(t) = ∥vi(t) − v0(t)∥ and eui(t) = ∥ui(t) − u0(t)∥. The multiagent network (7) with the virtual leader (6) is said to achieve third-order leader-following consensus if the solution of (8) satisfies lim t→+∞ exi(t) = 0, lim t→+∞ evi(t) = 0, and lim t→+∞ eui(t) = 0, i = 1,2, …, N for any initial condition.

Basing on graph theory, Lyapunov function method, matrix theory, and the proof of Theorem 1 in [11], we have the following theorem.

Theorem 4. Under Assumption 1, if there exists 0 < φ < 1 such that

()
where δk and μ are the maximum eigenvalues of matrices
()
()
respectively, then the third-order leader-following consensus in the multiagent network (7) is achieved.

Proof. Consider the following Lyapunov function:

()
For any t ∈ (tk−1, tk], the time derivative of V(e(t)) along the trajectory of (8) is
()
Moreover, for any t ∈ (tk−1, tk],
()

For , similar to the proof of Theorem 1 in [11], we have

()
that is,
()
Consequently, according to (10) and (15), we obtain
()
By recurrence, we have
()
Then,
()
Using Δtk = tk − tk−1 ≤ ρ < +∞ and (15),
()
that is,
()
Therefore, third-order leader-following consensus in the multiagent network (5) is achieved under the impulsive controllers (7).

Remark 5. According to the proof of Theorem 4, it is not necessary that all the graphs G1, G2, …, Gm have directed spanning tree.

On the basis of Gersgorin disk theorem [23], we get μ ≤ 2(γ + 1). For , accordingly, δk is equal to the maximum eigenvalue of (InN×nN + (Lτ(k) + Bτ(k)) ⊗ Ck) T(InN×nN + (Lτ(k) + Bτ(k)) ⊗ Ck). Therefore, we have the following Corollary 6 (recalling Δtk = tk − tk−1 ≤ ρ and P = {1,2, …, m}).

Corollary 6. Under Assumption 1, if there exists 0 < φ < 1 such that

()
where δ = sup {δk}, δk is the maximum eigenvalue of the matrix (InN×nN + (Lτ(k) + Bτ(k)) ⊗ Ck) T(InN×nN + (Lτ(k) + Bτ(k)) ⊗ Ck); then, the third-order leader-following consensus in the multiagent network (7) is achieved.

4. Numerical Simulations

In this section, we give some numerical examples to verify the theory results given in the previous section.

Consider the following nonlinear function f for multiagent network:
()
It is easy to verify that the nonlinear function f in (24) satisfies Assumption 1. (Let γ = 5).

Following, we consider that the topology of the multiagent network is switching (P = {1,2}).

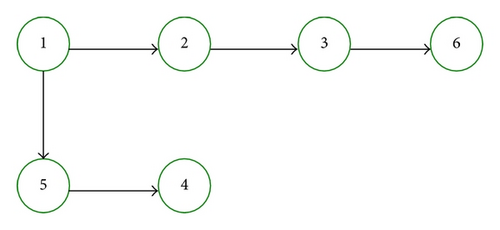
Example 7. Assume that the graphs G1, G2 have directed spanning trees. The directed spanning trees of G1, G2 are described in Figures 1 and 2. The corresponding matrices of the graphs G1, , G2, are A1, B1, A2, B2, respectively, where

()
In time intervals [t4k−1, t4k), the corresponding matrices are A2, B2, k = 1,2, …. In other time intervals, the corresponding matrices are A1, B1. We choose the impulsive gains Ck1, Ck2 with topology and , respectively, as follows:
()

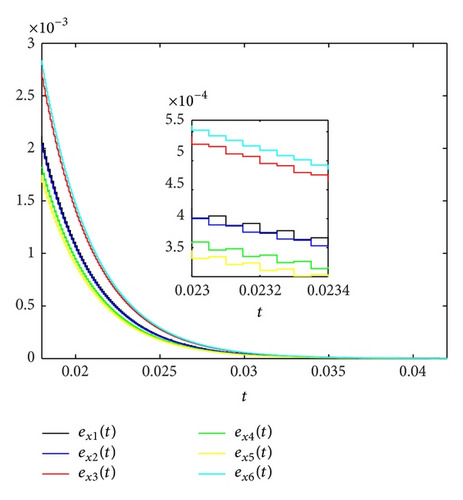
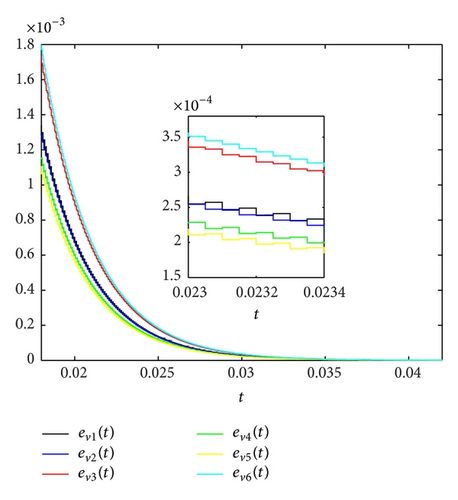
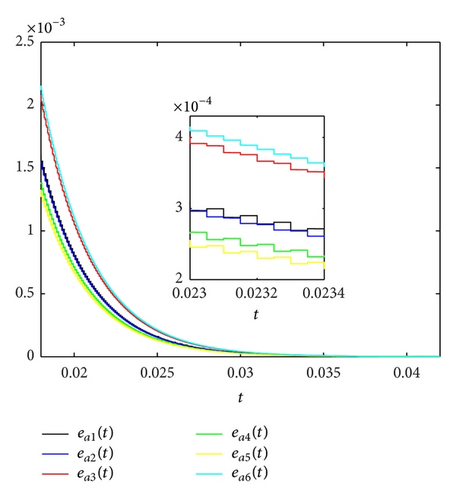
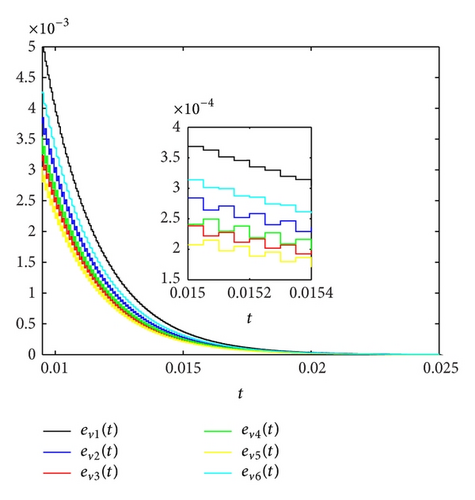
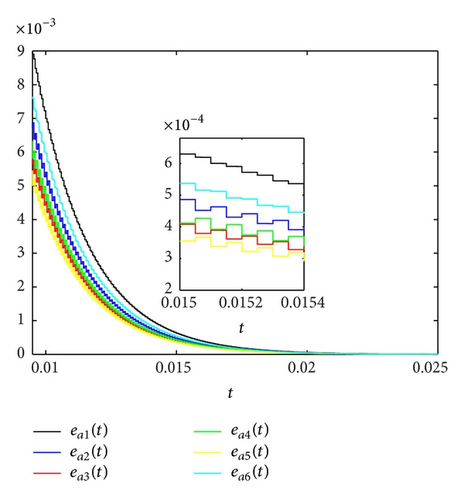
Let the equidistant impulsive interval Δtk = tk − tk−1 = 0.00005. Then, ρ = 0.00005. There exists φ = 0.9995, which satisfies the inequality (23) of Corollary 6. From Figures 3, 4, and 5, we can see that the position errors exi(t), the velocity errors evi(t), and the acceleration errors eai(t) converge to zero quickly.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Spanning tree of graph G1.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Spanning tree of graph G2.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Position errors exi(t) of system (7) with a directed spanning tree.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Velocity errors evi(t) of system (7) with a directed spanning tree.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Acceleration errors eai(t) of system (7) with a directed spanning tree.

Example 8. Assume that the graphs G1, G2 do not contain directed spanning trees. Let the corresponding matrices of the graphs G3, , G4, be A3, B3, A4, B4, respectively, where

()

Similar to Example 7, in time intervals [t4k−1, t4k), the corresponding matrices are A4, B4, k = 1,2, …, while in other time intervals, the corresponding matrices are A3, B3. We choose the impulsive gain Ck3, Ck4 with topology and , respectively, as follows:

()

Let the equidistant impulsive interval Δtk = tk − tk−1 = 0.00005. Then, ρ = 0.00005. By some calculations, we can know that there exists φ = 0.9995, which satisfies the inequality (23) of Corollary 6. From Figures 6, 7, and 8, we can see that the position errors exi(t), the velocity errors evi(t), and the acceleration errors eai(t) converge to zero quickly. It shows that the condition on a directed spanning tree is not necessary to realize consensus of the multiagent network (7) under the impulsive control. In addition, the researchers considered the second-order multiagent system with communication delay in [21, 22]. In our future work, we will study the third-order consensus problem for the multiagent systems with communication delay.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Position errors exi(t) of system (7) without a directed spanning tree.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Velocity errors evi(t) of system (7) without a directed spanning tree.
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Acceleration errors eai(t) of system (7) without a directed spanning tree.

5. Conclusion

By using graph theory, Lyapunov stability theory, and matrix theory, third-order leader-following consensus problem of a nonlinear multiagent network is studied in this paper. By designing proper impulsive controllers, a new criterion on realizing consensus in the multiagent network with switching topology is achieved. Finally, numerical simulations are provided to illustrate the theoretical results. In our future work, we will study the third-order consensus problem for the multiagent systems with communication delay.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (nos. 60964006, 61004101, and 11162004) and the Science Foundation of Guangxi Province, China (no. 2013GXNSFAA019006).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.