Volume 2013, Issue 1 598517

Research Article

Open Access

The Atom-Bond Connectivity Index of Catacondensed Polyomino Graphs

Jinsong Chen,

Corresponding Author

Jinsong Chen

[email protected]

College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350108, China fzu.edu.cn

College of Mathematics and Computer Science, Hunan Normal University, Changsha, Hunan 410081, China hunnu.edu.cn

Search for more papers by this author

Jianping Liu,

Jianping Liu

College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350108, China fzu.edu.cn

Search for more papers by this author

Qiaoliang Li,

Qiaoliang Li

College of Mathematics and Computer Science, Hunan Normal University, Changsha, Hunan 410081, China hunnu.edu.cn

Search for more papers by this author

Jinsong Chen,

Corresponding Author

Jinsong Chen

[email protected]

College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350108, China fzu.edu.cn

College of Mathematics and Computer Science, Hunan Normal University, Changsha, Hunan 410081, China hunnu.edu.cn

Search for more papers by this author

Jianping Liu,

Jianping Liu

College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350108, China fzu.edu.cn

Search for more papers by this author

Qiaoliang Li,

Qiaoliang Li

College of Mathematics and Computer Science, Hunan Normal University, Changsha, Hunan 410081, China hunnu.edu.cn

Search for more papers by this author

First published: 17 March 2013

https://doi.org/10.1155/2013/598517

Citations: 10

Academic Editor: Zhengkun Huan

Share a link

Email
Wechat
Bluesky

Abstract

Let G = (V, E) be a graph. The atom-bond connectivity (ABC) index is defined as the sum of weights over all edges uv of G, where d_u denotes the degree of a vertex u of G. In this paper, we give the atom-bond connectivity index of the zigzag chain polyomino graphs. Meanwhile, we obtain the sharp upper bound on the atom-bond connectivity index of catacondensed polyomino graphs with h squares and determine the corresponding extremal graphs.

1. Introduction

One of the most active fields of research in contemporary chemical graph theory is the study of topological indices (graph topological invariants) that can be used for describing and predicting physicochemical and pharmacological properties of organic compounds. In chemistry and for chemical graphs, these invariant numbers are known as the topological indices. There are many publications on the topological indices, see [1–6].

Let G = (V, E) be a simple graph of order n. A few years ago, Estrada et al. [7] introduced a further vertex-degree-based graph invariant, known as the atom-bond connectivity (ABC) index. It is defined as:

(1)

The ABC index keeps the spirit of the Randić index, and it provides a good model for the stability of linear and branched alkanes as well as the strain energy of cycloalkanes [7]. Recently, the study of the ABC index attracts some research attention [6, 8–12].

Polyomino graphs [13], also called chessboards [14] or square-cell configurations [15] have attracted some mathematicians’ considerable attention because many interesting combinatorial subjects are yielded from them such as domination problem and modeling problems of surface chemistry. A polyomino graph [16] is a connected geometric graph obtained by arranging congruent regular squares of side length 1 (called a cell) in a plane such that two squares are either disjoint or have a common edge. The polyomino graph has received considerable attentions.

Next, we introduce some graph definitions used in this paper.

Definition 1 (see [4].)Let G be a polyomino graph. If all vertices of G lie on its perimeter, then G is said to be catacondensed polyomino graph or tree-like polyomino graph. (see Figure 1).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The zigzag chain polyomino graph Z_h.

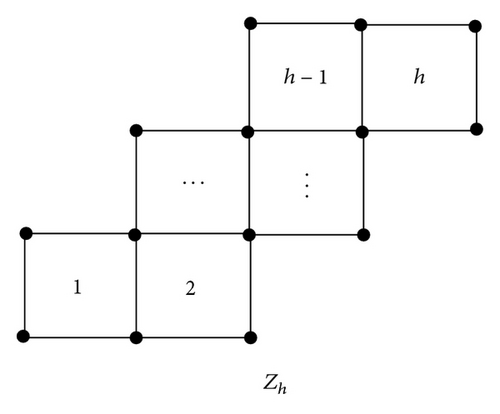
Definition 2 (see [16].)Let G be a chain polyomino graph with h squares. If the subgraph obtained from G by deleting all the vertices of degree 2 and all the edges adjacent to the vertices is a path, then G is said to be the zigzag chain polyomino graph, denoted by Z_h (see Figure 1).

In this paper, we give the ABC indices of the zigzag chain polyomino graphs with h squares and obtain the sharp upper bound on the ABC indices of catacondensed polyomino graphs with h squares and determine the corresponding extremal graphs.

2. The ABC Indices of Catacondensed Polyomino Graphs

Let

(2)

We call

the weight of the edge uv, denoted by W_uv.

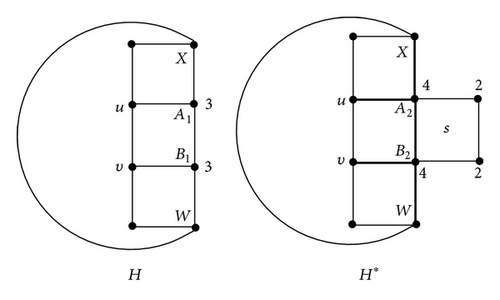
Note that for any catacondensed polyomino graph H^* with h squares, it can be obtained by gluing a new square s to some catacondensed polyomino graph H with h − 1 squares. So, we have the following lemma.

Lemma 3. Let H^* be a catacondensed polyomino graph with h squares which is obtained by gluing a new square s to some graph H, where H is a catacondensed polyomino graph with h − 1 squares. One has

(i)
If 2 ≤ h ≤ 3, then ABC(H^*) − ABC(H) ∈ S₁,
(ii)
if h ≥ 4, then ABC(H^*) − ABC(H) ∈ S₂.

Proof. Consider the following: (i) if 2 ≤ h ≤ 3, by directly calculating, we have ABC(H^*) − ABC(H) ∈ S₁,

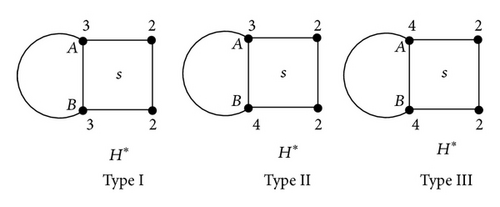
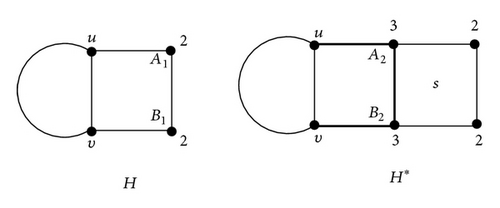
(ii) now, let h ≥ 4. Without the loss of generality, let square s be adjacent to the edge AB in H (see Figure 2). In the following, if the weights of some edges of H have been changed when s is adjacent to the edge AB in H, then we marked these edges with thick lines in H^*. Let D_i = ABC(H^*) − ABC(H) (i = 1,2, …, 35). Note that except the edge AB of s, the summation of the weights of the remaining three edges is always in H^*. There are exactly three types of formations (see Figure 2).

Case 1. In Type I, and (see Figure 3).

By the definition of ABC index, we have ABC(H^*) − ABC(H) = + + + = D_i (i = 1,2, 3).

If d_u = 3 and d_v = 3, then D₁ = 2.
If d_u = 3 and d_v = 4 or d_u = 4 and d_v = 3, then .
If d_u = 4 and d_v = 4, then .

Case 2. In Type II,

, and

. (see Figure 4).

Let u adjacent to A and v, w adjacent to B (see Figure 4). Then d_u ∈ {2,3, 4}, d_v ∈ {3,4}, and d_w ∈ {2,3, 4}. If d_u = 2, d_v = 3, and d_w = 2, which is in contradiction with h ≥ 4; if d_u = 3 and d_v = 3, which is in contradiction with ; if d_u = 4 and d_v = 3, which is in contradiction with (A ∈ V(H)).

By the definition of ABC index, we have ABC(H^*) − ABC(H) = + + + + = D_i (i = 4,5, …, 14).

If d_u = 2, d_v = 3, and d_w = 3, then .
If d_u = 2, d_v = 3, and d_w = 4, then .
If d_u = 2, d_v = 4, and d_w = 2, then .
If d_u = 2, d_v = 4, and d_w = 3, then .
If d_u = 2, d_v = 4, and d_w = 4, then .
If d_u = 3, d_v = 4, and d_w = 2, then .
If d_u = 3, d_v = 4, and d_w = 3, then .
If d_u = 3, d_v = 4, and d_w = 4, then .
If d_u = 4, d_v = 4, and d_w = 2, then .
If d_u = 4, d_v = 4, and d_w = 3, then .
If d_u = 4, d_v = 4, and d_w = 4, then .

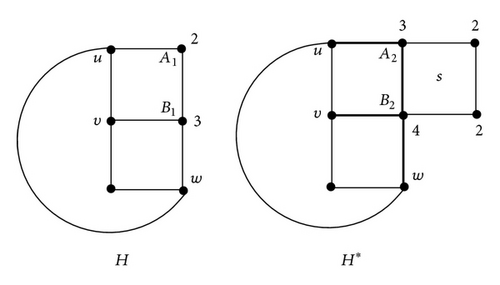
Case 3. In Type III, and (see Figure 5).

Let u, x adjacent to A and v, w adjacent to B (see Figure 5). Then, d_u ∈ {3,4}, d_v ∈ {3,4}, d_w ∈ {2,3, 4}, and d_x ∈ {2,3, 4}. Since the case d_u = 3, d_v = 4, d_x = y₁, and d_w = y₂ is the same as d_u = 4, d_v = 3, d_x = y₂, and d_w = y₁, where y₁, y₂ ∈ {2,3, 4}. And note that if d_u = d_v = 3 or d_u = d_v = 4, the vertices x and w are symmetric.

By the definition of ABC index, we have (i = 15,16, …, 35).

If d_u = d_v = 3, d_x = 2, and d_w = 3, then .
If d_u = d_v = 3, d_x = 2, and d_w = 4, then .
If d_u = d_v = 3, d_x = 3, and d_w = 3, then .
If d_u = d_v = 3, d_x = 3, and d_w = 4, then .
If d_u = d_v = 3, d_x = 4, and d_w = 4, then .
If d_u = d_v = 4, d_x = 2, and d_w = 2, then .
If d_u = d_v = 4, d_x = 2, and d_w = 3, then .
If d_u = d_v = 4, d_x = 2, and d_w = 4, then .
If d_u = d_v = 4, d_x = 3, and d_w = 3, then .
If d_u = d_v = 4, d_x = 3, and d_w = 4, then .
If d_u = d_v = 4, d_x = 4, and d_w = 4, then .
If d_u = 3, d_v = 4, d_x = 2, and d_w = 2, then .
If d_u = 3, d_v = 4, d_x = 2, and d_w = 3, then .
If d_u = 3, d_v = 4, d_x = 2, and d_w = 4, then .
If d_u = 3, d_v = 4, d_x = 3, and d_w = 2, then .
If d_u = 3, d_v = 4, d_x = 3, and d_w = 3, then .
If d_u = 3, d_v = 4, d_x = 3, and d_w = 4, then .
If d_u = 3, d_v = 4, d_x = 4, and d_w = 2, then .
If d_u = 3, d_v = 4, d_x = 4, and d_w = 3, then .
If d_u = 3, d_v = 4, d_x = 4, and d_w = 4, then .
If d_u = 3, d_v = 3, d_x = 2, and d_w = 2, then .

By directly calculating, we have D₅ = D₇, D₁₀ = D₁₂, D₁₆ = D₂₇ = D₂₉, D₁₈ = D₃₀, D₁₉ = D₂₃ = D₃₁ = D₃₃, D₂₁ = D₂₈ = D₃₂, D₂₄ = D₃₄, and D₆ = max _1≤i≤35D_i, D₁₄ = min _1≤i≤35D_i. So ABC(H^*) − ABC(H) ∈ S₂, where h ≥ 4.

Therefore, ABC(H^*) − ABC(H) ∈ S.

Description unavailable — **Figure 2**
Open in figure viewer PowerPoint

By Lemma 3, we have the following theorem.

Theorem 4. Let G be a catacondensed polyomino graph with h (h ≥ 2) squares, then

(3)

where a_i is a nonnegative integer for i = 1,2, …, 25 and

Proof. We prove Theorem 4 by the induction on h. If h = 2, by directly calculating, we have , where a_i = 0 (i = 1,2, …, 25). So, Theorem 4 holds for h = 2.

Assume that Theorem 4 holds for all catacondensed polyomino graphs with h − 1 (h − 1 ≥ 2) squares, that is,

(4)

where a_i is a nonnegative integer for i = 1,2, …, 25 and

We will prove that Theorem 4 holds for h in the following. Let G^* be a catacondensed polyomino graph with h squares. Without the loss of generality, G^* can be obtained from some catacondensed polyomino graph G with h − 1 squares by gluing a new square s to G. By Lemma 3, we have ABC(G^*) − ABC(G) ∈ S. It means that ABC(G^*) = ABC(G) + a, where a ∈ S. By the induction assumption and direct computation, we have

(5)

There exists some l ∈ {1,2, …, 25} such that

and

for j ≠ l (j ∈ {1,2, …, 25}). Obviously,

is a nonnegative integer for i = 1,2, …, 25 and

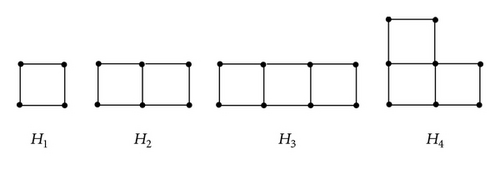
Lemma 5. Let H be a catacondensed polyomino graph with h squares. If h ≤ 3, there are exactly four nonisomorphism catacondensed polyomino graphs (see Figure 6), where , , , .

Theorem 6. Let Z_h be a zigzag chain polyomino graph with h squares, then

(6)

Proof. Obviously, Z_h can be obtained by gluing a new square s_h to Z_h−1. Let s_h−1 be the square adjacent to s_h (see Figure 1). We will prove Theorem 6 by the induction on h.

If h = 1,2, 3, then Theorem 6 holds (by Lemma 5). Assume that for h − 1 ≥ 3. By the induction assumption and the D₆ in Lemma 3, we have

(7)

So, Theorem 6 holds.

Note that D₆ = max _1≤i≤35 D_i for h ≥ 4 and by Lemma 5, we obtain the following Theorem 7.

Theorem 7. Let G be a catacondensed polyomino graph with h squares, then , with the equality if and only if G≅Z_h.

Acknowledgments

The project was supported by NSFC (no. 11071272; 11101086; 11101087) and the Foundation of Fuzhou University (no. 2012-XQ-30).

References

1 Behtoei A., Jannesari M., and Taeri B., Maximum Zagreb index, minimum hyper-Wiener index and graph connectivity, Applied Mathematics Letters. (2009) 22, no. 10, 1571–1576, https://doi.org/10.1016/j.aml.2009.05.001, MR2561738, ZBL1171.05350.
Google Scholar
2 Das K. C., Gutman I., and Furtula B., Survey on geometric-arithmetic indices of graphs, MATCH Communications in Mathematical and in Computer Chemistry. (2011) 65, no. 3, 595–644, MR2829382.
Google Scholar
3 Liu B. and Gutman I., On general Randić indices, MATCH Communications in Mathematical and in Computer Chemistry. (2007) 58, no. 1, 147–154, MR2335485, ZBL1193.92089.
Google Scholar
4 Liu B. and You Z., A survey on comparing Zagreb indices, MATCH Communications in Mathematical and in Computer Chemistry. (2011) 65, no. 3, 581–593, MR2829381.
Web of Science® Google Scholar
5 Liu J. and Liu B., E-L equienergetic graphs, Communications in Mathematical and in Computer Chemistry. (2011) 66, no. 3, 971–976, MR2884779.
Google Scholar
6 Zhou B. and Trinajstic N., Further results on atom-bond connectivity index of trees, Chemical Physics Letters. (2008) 455, 120–123.
Google Scholar
7 Estrada E., Torres L., Rodriguez L., and Gutman I., An atom-bond connectivity index: modelling the enthalpy of formation of alkanes, Indian Journal of Chemistry A. (1998) 37, 849–855.
Google Scholar
8 Chen J. and Guo X., Extreme atom-bond connectivity index of graphs, MATCH Communications in Mathematical and in Computer Chemistry. (2011) 65, no. 3, 713–722, MR2829389.
Web of Science® Google Scholar
9 Chen J. and Guo X., The atom-bond connectivity index of chemical bicyclic graphs, Applied Mathematics B. (2012) 27, no. 2, 243–252, MR2928711.
Google Scholar
10 Chen J., Liu J., and Guo X., Some upper bounds for the atom-bond connectivity index of graphs, Applied Mathematics Letters. (2012) 25, no. 7, 1077–1081, https://doi.org/10.1016/j.aml.2012.03.021, MR2915128, ZBL1246.05091.
Web of Science® Google Scholar
11 Furtula B., Graovac A., and Vukičević D., Atom-bond connectivity index of trees, Discrete Applied Mathematics. (2009) 157, no. 13, 2828–2835, https://doi.org/10.1016/j.dam.2009.03.004, MR2537484, ZBL1209.05252.
Web of Science® Google Scholar
12 Xing R., Zhou B., and Du Z., Further results on atom-bond connectivity index of trees, Discrete Applied Mathematics. (2010) 158, no. 14, 1536–1545, https://doi.org/10.1016/j.dam.2010.05.015, MR2659168, ZBL1216.05161.
Google Scholar
13 Berge C., Chen C. C., Chvátal V., and Seow C. S., Combinatorial properties of polyominoes, Combinatorica. (1981) 1, no. 3, 217–224, https://doi.org/10.1007/BF02579327, MR637826, ZBL0491.05048.
Google Scholar
14 Cockayne E. J., Chessboard domination problems, Discrete Mathematics. (1990) 86, no. 1–3, 13–20, https://doi.org/10.1016/0012-365X(90)90344-H, MR1088555, ZBL0818.05057.
Google Scholar
15 Harary F. and Mezey P., Cell-shedding transformations, equivalence relations, and similarity measures for square-cell configurations, International Journal of Quantum Chemistry. (1997) 62, 353–361.
Google Scholar
16 Chen R., Perfect matchings of generalized polyomino graphs, Graphs and Combinatorics. (2005) 21, no. 4, 515–529, https://doi.org/10.1007/s00373-005-0624-1, MR2209180, ZBL1089.05061.
Google Scholar

Citing Literature

All articles

The Atom-Bond Connectivity Index of Catacondensed Polyomino Graphs

Abstract

1. Introduction

2. The ABC Indices of Catacondensed Polyomino Graphs

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Atom-Bond Connectivity Index of Catacondensed Polyomino Graphs

Abstract

1. Introduction

2. The ABC Indices of Catacondensed Polyomino Graphs

Acknowledgments

References

Citing Literature

Figures

References

Related

Information