Abstract and Applied Analysis
Volume 2013, Issue 1 597807
Research Article
Open Access

A New Integro-Differential Equation for Rossby Solitary Waves with Topography Effect in Deep Rotational Fluids

Hongwei Yang, 

Hongwei Yang

Information School, Shandong University of Science and Technology, Qingdao 266590, China sdust.edu.cn

Search for more papers by this author
Qingfeng Zhao, 

Qingfeng Zhao

Information School, Shandong University of Science and Technology, Qingdao 266590, China sdust.edu.cn

Search for more papers by this author
Baoshu Yin, 

Corresponding Author

Baoshu Yin

Institute of Oceanology, China Academy of Sciences, Qingdao 266071, China cas.cn

Key Laboratory of Ocean Circulation and Wave, Chinese Academy of Sciences, Qingdao 266071, China cas.cn

Search for more papers by this author
Huanhe Dong, 

Huanhe Dong

Information School, Shandong University of Science and Technology, Qingdao 266590, China sdust.edu.cn

Search for more papers by this author
First published: 30 September 2013
https://doi.org/10.1155/2013/597807
Citations: 11
Academic Editor: Rasajit Bera

Abstract

From rotational potential vorticity-conserved equation with topography effect and dissipation effect, with the help of the multiple-scale method, a new integro-differential equation is constructed to describe the Rossby solitary waves in deep rotational fluids. By analyzing the equation, some conservation laws associated with Rossby solitary waves are derived. Finally, by seeking the numerical solutions of the equation with the pseudospectral method, by virtue of waterfall plots, the effect of detuning parameter and dissipation on Rossby solitary waves generated by topography are discussed, and the equation is compared with KdV equation and BO equation. The results show that the detuning parameter α plays an important role for the evolution features of solitary waves generated by topography, especially in the resonant case; a large amplitude nonstationary disturbance is generated in the forcing region. This condition may explain the blocking phenomenon which exists in the atmosphere and ocean and generated by topographic forcing.

1. Introduction

Among the many wave motions that occur in the ocean and atmosphere, Rossby waves play one of the most important roles. They are largely responsible for determining the ocean’s response to atmospheric and other climate changes [1]. In the past decades, the research on nonlinear Rossby solitary waves had been given much attention in the mathematics and physics, and some models had been constructed to describe this phenomenon. Based upon the pioneering work of Long [2] and Benney [3] on barotropic Rossby waves, there had been remarkably exciting developments [4–11] and formed classical solitary waves theory and algebraic solitary waves theory. The so-called classical solitary waves indicate that the evolution of solitary waves is governed by the Korteweg-de Vries (KdV) type model, while the behavior of solitary waves is governed by the Benjamin-Ono (BO) model, it is called algebraic solitary waves. After the KdV model and BO model, a more general evolution model for solitary waves in a finite-depth fluid was given by Kubota, and the model was called intermediate long-wave (ILW) model [12, 13]. Many mathematicians solved the above models by all kinds of method and got a series of results [14–19]. We note that most of the previous researches about solitary waves were carried out in the zonal area and could not be applied directly to the spherical earth, and little attention had been focused on the solitary waves in the rotational fluids [20]. Furthermore, as everyone knows the real oceanic and atmospheric motion is a forced and dissipative system. Topography effect as a forcing factor has been studied by many researchers [21–25]; on the other hand, dissipation effect must be considered in the oceanic and atmospheric motion; otherwise, the motion would grow explosively because of the constant injecting of the external forcing energy. Our aim is to construct a new model to describe the Rossby solitary waves in rotational fluid with topography effect and dissipation effect. It has great difference from the previous researches.

In this paper, from rotational potential vorticity-conserved equation with topography effect and dissipation effect, with the help of the multiple-scale method, we will first construct a new model to describe Rossby solitary waves in deep rotational fluids. Then we will analyse the conservation relations of the model and derive the conservation laws of Rossby solitary waves. Finally, the model is solved by the pseudospectral method [26]. Based on the waterfall plots, the effect of detuning parameter and dissipation on Rossby solitary waves generated by topography are discussed, the model is compared with KdV model and BO model, and some conclusions are obtained.

2. Mathematics Model

According to [27], taking plane polar coordinates (r, θ), r pointing to lower latitude is positive and the positive rotation is counter-clockwise, and then the rotational potential vorticity-conserved equation including topography effect and turbulent dissipation is, in the nondimensional form, given by
()
where Ψ is the dimensionless stream function; β = (ω0/R0)cos ϕ0(L2/U), in which R0 is the Earth’s radius, ω0 is the angular frequency of the Earth’s rotation, ϕ0 is the latitude, L and U are the characteristic horizontal length and velocity scales, h(r, θ) expresses the topography effect, λ0[(1/r)(∂/∂r)(r(∂Ψ/∂r)) + (1/r2)(∂2Ψ/∂θ2)] denotes the vorticity dissipation which is caused by the Ekman boundary layer and λ0 is a dissipative coefficient, Q is the external source, and the form of Q will be given in the latter.
In order to consider weakly nonlinear perturbation on a rotational flow, we assume
()
where α is a small disturbance in the basic flow and reflects the proximity of the system to a resonate state; c is a constant, which is regarded as a Rossby waves phase speed; ψ denotes disturbance stream function; Ω(r) expresses the rotational angular velocity. In order to consider the role of nonlinearity, we assume the following type of rotational angular velocity:
()
where ω1 is constant and ω(r) is a function of r. For simplicity, ω(r) is assumed to be smooth across r = r2.
In the domain [r1, r2], in order to achieve a balance among topography effect, turbulent dissipation, and nonlinearity and to eliminate the derivative term of dissipation, we assume
()
Substituting (2), (3), and (4) into (1) leads to the following equation for the perturbation stream function ψ:
()
In the domain [r2, ∞], the parameter β is smaller than that in the domain [r1, r2], and we assume β = 0 for [r2, ∞]. Furthermore, the turbulent dissipation and topography effect are absent in the domain and only consider the features of disturbances generated. Substituting (2) and (3) into (1), we have the following governing equations:
()
For (5), we introduce the following stretching transformations:
()
and the perturbation expansion of is in the following form:
()
Substituting (7) and (8) into (5), comparing the same power of ε term, we can obtain the ε1/2 equation:
()
where the operator ℒ is defined as
()
Assume the perturbation at boundary r = r1 does not exist, that is,
()
and the perturbation at boundary r = r2 is determined by (6). For the linear solution to be separable, assuming the solution of (9) in the form:
()
thus ϕ(r) should satisfy the following equation:
()
On the other hand, we proceed to the ε3/2 equation:
()
Multiplying the both sides of (14) by rϕ/(ω  −  c) and integrating it with respect to r from r1 to r2, employing the boundary conditions (11), we get
()
In (15), if the boundary conditions on ϕ and ψ2 are known, the equation governing the amplitude A will be determined. Assuming the solution of (5) matches smoothly with the solution of (6) at r = r2, we can solve (6) to seek the solution at r = r2.
For (6), we adopt the transformations in the forms:
()
and the perturbation function is shown ; then by substituting (16) into (6), we can get the ε0 equation:
()
It is easy to find that (17) can reduce to
()
Obviously, the solution of (18) is
()
Taking the derivative with respect to r for both sides of (19) leads to
()
Because the solution of (5) matches smoothly with the solution of (6) at r = r2, we obtain
()
()
From (21), we have
()
Substituting (23) into (20) leads to
()
where . Then, based on (22) and (24), we get
()
Substituting the boundary conditions (23) and (25) into (15) yields
()
Equation (26) can be rewritten as follows:
()
where and a = − c))(d/dr)(r(dϕ/dr))dr, a1 = , a2 = , a3 = r2ϕ2(r2)/a, G = . Equation (27) is an integro-differential equation and λA expresses dissipation effect and has the same physical meaning with the term ∂2A/∂Θ2 in Burgers equation. When a3 = λ = H = 0, the equation degenerates to the KdV equation. When a2 = λ = H = 0, the equation degenerates to the so-called rotational BO equation. Here we call (27) forced rotational KdV-BO-Burgers equation. As we know, the forced rotational KdV-BO-Burgers equation as a governing model for Rossby solitary waves is first derived in the paper.

3. Conservation Laws

In this section, the conservation laws are used to explore some features of Rossby solitary waves. In [7], Ono presented four conservation laws of BO equation, and we extend Ono’s work to investigate the following questions: Has the rotational KdV-BO-Burgers equation also conservation laws without dissipation effect? Has it four conservation laws or more? How to change of these conservation quantities in the presence of dissipation effect?

In this section, topography effect is ignored; that is, H is taken zero in (27). Based on periodicity condition, we assume that the values of A, AΘ, AΘΘ, AΘΘΘ at Θ = 0 equal that at Θ = 2π. Then integrating (27) with respect to Θ over (0,2π), we are easy to obtain the following conservation relation:
()
From (28), it is obvious that Q1 decreases exponentially with the evolution of time T and the dissipation coefficient λ. By analogy with the KdV equation, Q1 is regarded as the mass of the solitary waves. This shows that the dissipation effect causes the mass of solitary waves decrease exponentially. When dissipation effect is absent, the mass of the solitary waves is conserved.
In what follows, (27) has another simple conservation law, which becomes clear if we multiply (27) by A(Θ, T) and carry the integration; by using the property of the operator , then we get
()
Similar to the mass Q1, Q2 is regarded as the momentum of the solitary waves and is conserved without dissipation. The momentum of the solitary waves also decreases exponentially with the evolution of time T and the increasing of dissipative coefficient λ in the presence of dissipation effect. Furthermore, the rate of decline of momentum is faster than the rate of mass.
Next, we multiply (27) by (A2 − (a3/a1)ℋ(AΘ)) and obtain
()
Then taking the derivative of (27) with respect to Θ and multiplying (−(2a2/a1)AΘ + (a3/a1)ℋ(A)) lead to
()
Adding (30) to (31), by virtue of the property of operator ℋ:
()
we have
()
Taking , we are easy to see that when the dissipation effect is absent, that is, λ = 0, Q3 is a conserved quantity and regarded as the energy of the solitary waves. So we can conclude that the energy of solitary waves is conserved without dissipation. By analysing (33), we can find the decreasing trend of energy of solitary waves.
Finally, let us consider a quantity related to the phase of solitary waves:
()
and we can get without dissipation. According [7], we present the velocity of the center of gravity for the ensemble of such waves ; by employing dQ1/dT = 0 and , we have dQ4/dT = 0, which shows that the velocity of the center of gravity is conserved without dissipation.
After the four conservation relations are given, we can proceed to seek the fifth conservation quantity. In fact, after tedious calculation, we can also verify that
()
is also conservation quantity. According the idea, we can obtain the sixth conservation quantity Q6 and the seventh conservation quantity Q7…, so we can guess that, similar to the KdV equation, the rotational KdV-BO-Burgers equation without dissipation also owns infinite conservation laws, but it needs to be verified in the future.

4. Numerical Simulation and Discussion

In this section, we will take into account the generation and evolution feature of Rossby solitary waves under the influence of topography and dissipation, so we need to seek the solutions of forced rotational KdV-BO-Burgers equation. But we know that there is no analytic solution for (27), and here we consider the numerical solutions of (27) by employing the pseudospectral method.

The pseudo-spectral method uses a Fourier transform treatment of the space dependence together with a leap-forg scheme in time. For ease of presentation the spatial period is normalized to [0,2π]. This interval is divided into 2N points, and then ΔT = π/N. The function A(X, T) can be transformed to the Fourier space by
()
The inversion formula is
()
These transformations can use Fast Fourier Transform algorithm to efficiently perform. With this scheme, ∂A/∂X can be evaluated as F−1{ivFA}, ∂3A/∂X3 as −iF−1{v3FA}, ∂H/∂X as F−1{ivFH}, and so on. Combined with a leap-frog time step, (27) would be approximated by
()
The computational cost for (38) is six fast Fourier transforms per time step.

Once the zonal flow Ω(r) and the topography function H(r, Θ) as well as dissipative coefficient λ are given, it is easy to get the coefficients of (27) by employing (13). In order to simplify the calculation and to focus attention on the time evolution of the solitary waves with topography effect and dissipation effect and to show the difference among the KdV model, BO model, and rotational KdV-BO model, we take a1 = 1, a2 = −1, and a3 = −1. As an initial condition, we take A(X, 0) = 0. In the present numerical computation, the topography forcing is taken as .

4.1. Effect of Detuning Parameter α and Dissipation

In Figure 1, we consider the effect of detuning parameter α on solitary waves. The evolution features of solitary waves generated by topography are shown in the absence of dissipation with different detuning parameter α. It is easy to find from these waterfall plots that the detuning parameter α plays an important role for the evolution features of solitary waves generated by topography.

Details are in the caption following the image
Figure 1 (a) α = 2.5 
Open in figure viewerPowerPoint
Solitary waves generated by topography in the absence of dissipation.
Details are in the caption following the image
Figure 1 (b) α = 0
Open in figure viewerPowerPoint
Solitary waves generated by topography in the absence of dissipation.
Details are in the caption following the image
Figure 1 (c) α = −2.5
Open in figure viewerPowerPoint
Solitary waves generated by topography in the absence of dissipation.

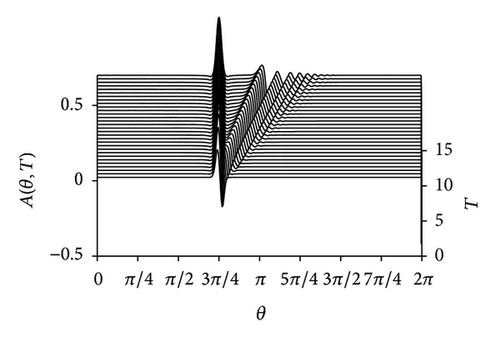
When α > 0 (Figure 1(a)), a positive stationary solitary wave is generated in the topographic forcing region, and a modulated cnoidal wave-train occupies the downstream region. There is no wave in the upstream region. A flat buffer region exists between the solitary wave in the forcing region and modulated cnoidal wave-train in the downstream. With the detuning parameter α decreasing, the amplitudes of both solitary wave in the forcing region and modulated cnoidal wave-train in the downstream region increase and the modulated cnoidal wave-train closes to the forcing region gradually and the flat buffer region disappears slowly.

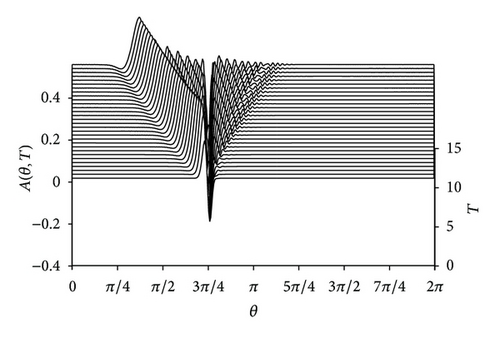
Up to α = 0 (Figure 1(b)), the resonant case forms. In this case, a large amplitude nonstationary disturbance is generated in the forcing region. To some degree, this condition may explain the blocking phenomenon which exists in the atmosphere and ocean and generated by topographic forcing.

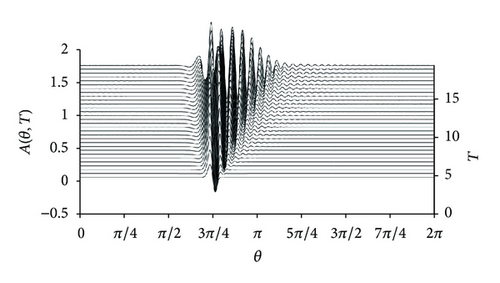
As α < 0, from Figure 1(c) we can easy to find that a negative stationary solitary wave is generated in the forcing region, and this is great difference with the former two conditions. Meanwhile, there are both wave-trains in the upstream and downstream region. The amplitude and wavelength of wave-train in the upstream region are larger than those in the downstream regions. Similar to Figure 1(b) and unlike Figure 1(a), the wave-trains in the upstream and downstream regions connect to the forcing region and the flat buffer region disappears.

Figure 2 shows the solitary waves generated by topography in the presence of dissipation with dissipative coefficient λ = 0.3 and detuning parameter α = 2.5. The conditions of α = 0 and α < 0 are omitted. Compared to Figure 1(a), we will find that there is also a solitary wave generated in the forcing region, but because of dissipation effect the amplitude of solitary wave in the forcing region decreases as the dissipative coefficient λ increases (Figures omitted) and time evolution. Meanwhile, the modulated cnoidal wave-train in the downstream region is dissipated. When λ is big enough, the modulated cnoidal wave-train in the downstream region disappears.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Solitary waves generated by topography in the presence of dissipation (λ = 0.3, α = 2.5).

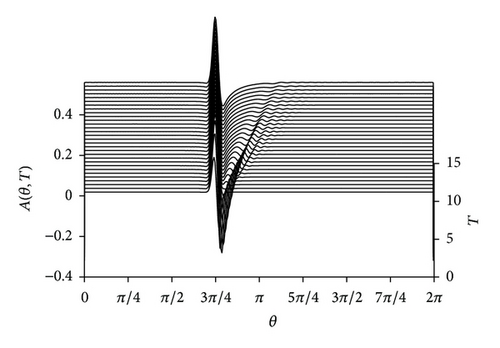
4.2. Comparison of KdV Model, BO Model, and KdV-BO Model

We know that the rotation KdV-BO equation reduces to the KdV equation as a3 = 0 and to the BO equation as a2 = 0, so, in this subsection by comparing Figure 1(a) with Figure 3, we will look for the difference of solitary waves which is described by KdV-BO model, KdV model, and BO model. The role of detuning parameter α and dissipation effect has been studied in the former subsection, so here we only consider the condition of λ = 0, α = 2.5.

Details are in the caption following the image
Figure 3 (a) KdV model (a3 = 0,   α = 2.5,   λ = 0)
Open in figure viewerPowerPoint
Comparison of KdV model, Bo model, and KdV-BO model.
Details are in the caption following the image
Figure 3 (b) BO model (a2 = 0,   α = 2.5,   λ = 0)
Open in figure viewerPowerPoint
Comparison of KdV model, Bo model, and KdV-BO model.

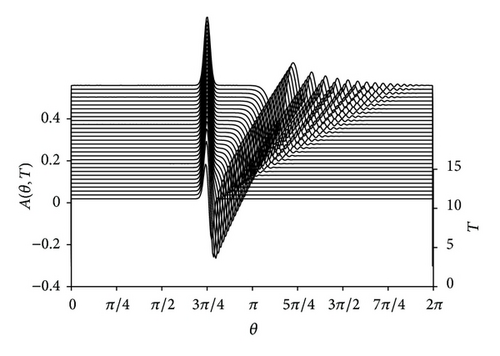
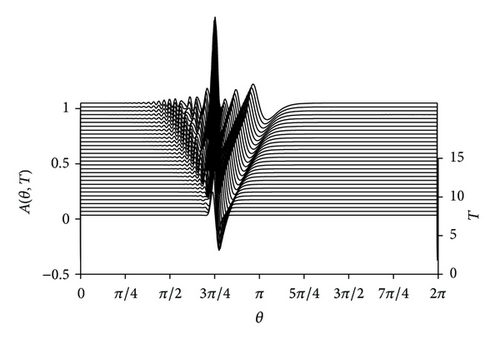
At first, we can find that a positive solitary wave is all generated in the forcing region in Figures 1(a), 3(a) and 3(b), but it is stationary in Figures 1(a) and 3(a), and is nonstationary in Figure 3(b). By surveying carefully we find that the amplitude of stationary wave in the forcing region in Figure 1(a) is larger than that in Figure 3(a). Additionally, a modulated cnoidal wave-train is excited in the downstream region in Figures 1(a) and 3(a), and in both downstream and upstream region in Figure 3(b). The amplitude of modulated cnoidal wave-train in downstream region in Figure 3(b) is the largest and in Figure 1(a) is the smallest among the three models. Furthermore, in Figure 3(a) the wave number of modulated cnoidal wave-train is more than that in Figures 1(a) and 3(b). In a word, by the above analysis and comparison, it is easy to find that Figure 1(a) is similar to Figure 3(a) and has great difference with Figure 3(b). This indicates that the term a2(∂3A/∂Θ3) plays more important role than the term a3(∂2/∂Θ2)ℋ(A) in rotational KdV-BO equation.

5. Conclusions

In this paper, we presented a new model: rotational KdV-BO-Burgers model to describe the Rossby solitary waves generated by topography with the effect of dissipation in deep rotational fluids. By analysis and computation, five conservation quantities of KdV-BO-Burgers model were derived and corresponding four conservation laws of Rossby solitary waves were obtained; that is, mass, momentum, energy, and velocity of the center of gravity of Rossby solitary waves are conserved without dissipation effect. Further, we presented that the rotational KdV-BO-Burgers equation owns infinite conservation quantities in the absence of dissipation effect. Detailed numerical results obtained using pseudospectral method are presented to demonstrate the effect of detuning parameter α and dissipation. By comparing the KdV model, BO model, and KdV-BO model, we drew the conclusion that the term a2(∂3A/∂Θ3) plays more important role than the term a3(∂2/∂Θ2)ℋ(A) in rotational KdV-BO equation. More problems on KdV-BO-Burgers equation such as the analytical solutions, integrability, and infinite conservation quantities are not studied in the paper due to limited space. In fact, there are many methods carried out to solve some equations with special nonhomogenous terms [28] as well as multiwave solutions and other form solution [29, 30] of homogenous equation. These researches have important value for understanding and realizing the physical phenomenon described by the equation and deserve to carry out in the future.

Acknowledgments

This work was supported by Innovation Project of Chinese Academy of Sciences (no. KZCX2-EW-209), National Natural Science Foundation of China (nos. 41376030 and 11271107), Nature Science Foundation of Shandong Province of China (no. ZR2012AQ015), Science and Technology plan project of the Educational Department of Shandong Province of China (no. J12LI03), and SDUST Research Fund (no. 2012KYTD105).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.