International Journal of Partial Differential Equations
Volume 2013, Issue 1 590737
Research Article
Open Access

A Posteriori Regularization Parameter Choice Rule for Truncation Method for Identifying the Unknown Source of the Poisson Equation

Xiao-Xiao Li, 

Corresponding Author

Xiao-Xiao Li

School of Science, Lanzhou University of Technology, Lanzhou, Gansu 730050, China lzu.edu.cn

Search for more papers by this author
Dun-Gang Li, 

Dun-Gang Li

School of Science, Lanzhou University of Technology, Lanzhou, Gansu 730050, China lzu.edu.cn

Search for more papers by this author
First published: 19 September 2013
https://doi.org/10.1155/2013/590737
Academic Editor: Athanasios N. Yannacopoulos

Abstract

We consider the problem of determining an unknown source which depends only on one variable in two-dimensional Poisson equation. We prove a conditional stability for this problem. Moreover, we propose a truncation regularization method combined with an a posteriori regularization parameter choice rule to deal with this problem and give the corresponding convergence estimate. Numerical results are presented to illustrate the accuracy and efficiency of this method.

1. Introduction

Inverse source problems arise in many branches of science and engineering, for example, heat conduction, crack identification, electromagnetic theory, geophysical prospecting, and pollutant detection. In this paper, we consider the following inverse problem: to find a pair of functions (u(x, y), f(x)) satisfying
()
where f(x) is the unknown source depending only on one spatial variable and u(x, 1) = g(x) is the supplementary condition. In applications, input data g(x) can only be measured, and there will be measured data function gδ(x) which is merely in L2(0, π) and satisfies
()
where the constant δ > 0 represents a bound on the measurement error.

For the heat equation, there has been a large number of research results for the different forms of heat source [1–6]. In [7], the authors identified the unknown source of the Poisson equation using the modified regularization method. In [8], the authors identified the unknown source of the Poisson equation using the truncation method. In [7, 8], the regularization parameters which depend on the noise level and the a priori bound are selected by the a priori rule. Generally speaking, there is a defect for any a priori method; that is, the a priori choice of the regularization parameter depends seriously on the a priori bound E of the unknown solution. However, in general, the a priori bound E cannot be known exactly in practice, and working with a wrong constant E may lead to the bad regularized solution.

In the present paper, a posteriori choice of the regularization parameter will be given. To the authors’ knowledge, there are few papers for choosing the regularization parameter by the a posteriori rule for this problem.

The truncation regularization methods have been studied for solving various types of inverse problems. Eldén et al. [9] used the truncation method to analyze and compute one-dimensional IHCP, Xiong et al. [10] used it to consider the surface heat flux for the sideways heat equation, Fu et al. [11] used it to solve the BHCP, Qian et al. [12] used it to consider the numerical differentiation, and Regińska and Regiński [13] applied the idea of truncation to a Cauchy problem for the Helmholtz equation. In [9–13], the ill-posedness of the problem was caused by the high frequency components, and they all used the truncation method to eliminate all high frequencie and called this truncation method Fourier method. In [14], the authors ever identified the unknown source on Poisson equation on half unbounded domain using Fourier Transform. In this paper, we identified the unknown source on Poisson equation on half band domain using separation of variables and gave the numerical example to illustrate our methods. In [15], the authors ever used this method to consider a Cauchy problem for the Laplace equation in the bounded domain and obtained the error estimate which had a good convergence rate. The truncation method of this paper seems to be more direct and simple for considering the inverse problem in the bounded or half band domain.

This paper is organized as follows. The ill-posedness of this problem (1) is analyzed in Section 2. In Section 3, we give a conditional stable result. In Section 4, we propose the truncation method and give the convergence estimates under an a priori assumption for the exact solution and the a posteriori regularization parameter choice rule. In Section 5, a numerical example is proposed to show the effectiveness for this method. Section 6 puts an end to this paper with a brief conclusion.

2. Ill-Posedness of Problem (1)

By separation of variables, we obtain that the solution of problem (1) has the form
()
where
()
is an orthogonal basis in L2(0, π), and
()
Using the supplementary condition, we have
()
Defining the operator K : f → g, we obtain
()
It is easy to see that K is a linear compact operator, and the singular values of K satisfy
()
That is,
()
Therefore,
()
Note that 1/σn = O(n2) as n → ∞; thus, the exact data function g(x) must satisfy the property that (g, Xn) decays rapidly as O(n−2). As for the measured data function gδ(x), we cannot expect that it has the same decay rate in L2(0, π). Thus, the problem (1) is ill-posed. It is impossible to gain the unknown source using classical methods. In the following section, we will use the truncation regularization method to deal with the ill-posed problem. Before doing that, we impose an a priori bound on the heat source; that is,
()
where E > 0 is a constant, denotes the norm in Sobolev space, Hp(0, π) is defined by [16] as following:
()
For any ill-posed problem, the a-priori bound of the exact solution is very necessary. Otherwise, the regularization solution is not convergent or the rate of convergence is very slow. The detail of the a priori bound can be seen in [17].

3. A Conditional Stability Estimate

We firstly establish a conditional stability estimate for the inverse source problem (1).

Lemma 1. If n ≥ 1, one has the following inequality:

()

Theorem 2. Assume that f(x) is the solution of (1) and condition (11) is satisfied; then, the following estimate holds:

()

Proof. Using the Hölder inequality and (11), we obtain

()
So
()

Remark 3. If f1, f2 are the solutions of the inverse source problem with exact data g1, g2, respectively, then there holds

()
It is obvious that if , then .

4. An A Posteriori Regularization Parameter Choice Rule for the Truncation Method and Convergence Estimate

Noting (10), small errors in the components of large n can blow up and completely destroy the solution. A nature way to stabilize the problem is to eliminate all the components of large n from the solution and instead consider (10) only for n ≤ N. Then, we get a regularized solution
()
Noting (18), if the parameter N is large, fδ,N(x) is close to the exact solution f(x). On the other hand, if the parameter N is fixed, fδ,N(x) is bounded. So the positive integer N plays the role of regularization parameter. We consider an a posteriori regularization parameter choice by the discrepancy principle. Define
()
Due to the discrepancy principle, we will take N = N(δ, gδ) as the solution of
()
where τ > 1 is a constant. Before giving the main conclusion of this section, we first give an important lemma.

Lemma 4. Let condition (2) hold. If N is taken as the solution of (20), then one has the following inequality:

()

Proof. Due to (2) and (19), we obtain

()
So
()
On the other hand,
()
So
()
Combining (23) with (25), we obtain
()

The main conclusion of this paper is as the following.

Theorem 5. Let fδ,N(x) be the regularized solution given by (18), and let f(x) be the exact solution given by (10). Let gδ(x) be the measured data at y = 1 satisfying (2), and priori condition (11) holds for p > 0. If the regularization parameter N is chosen as the solution of (20), then one gets the following estimate:

()
where C = (e/(e − 1)) p/(p+2)(τ + 1) p/(p+2) + (e/(e − 1))(1/(τ − 1)) 2/(p+2).

Proof. Due to the triangle inequality, we obtain

()
where . It is easy to know
()
Due to triangle inequality and (20), we have
()
Using Theorem 2, we obtain
()
Using (18), we obtain
()
Due to (13), (21), and (32), we obtain
()
Combining (28), (31) and (33), we obtain
()
where C = (e/(e − 1)) p/(p+2)(τ + 1) p/(p+2) + (e/(e − 1))(1/(τ − 1)) 2/(p+2).

5. Numerical Implementation

From (7), we know that
()
We use the trapezoidal rule to approach the integral and do an approximate truncation for the series by choosing the sum of the front M + 1 terms. After considering an equidistant grid 0 = x1 < ⋯<xM+1 = π, (xi = ((i − 1)/M)π, i = 1, …, M + 1), we get
()
where
()
The bisection method is used to solve (20) and τ = 1.1.

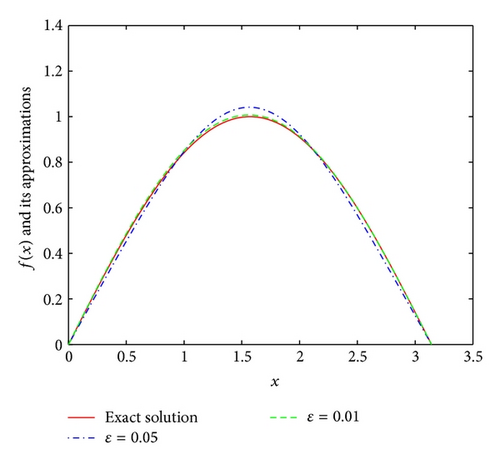
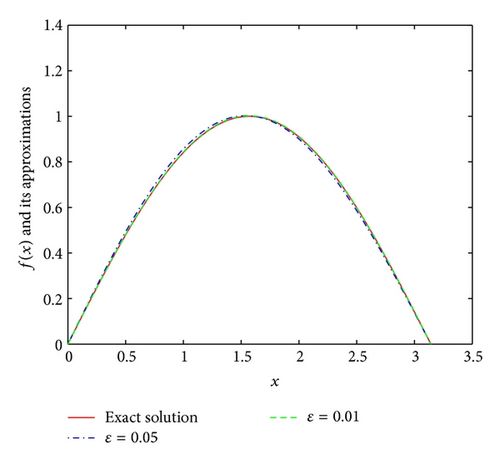
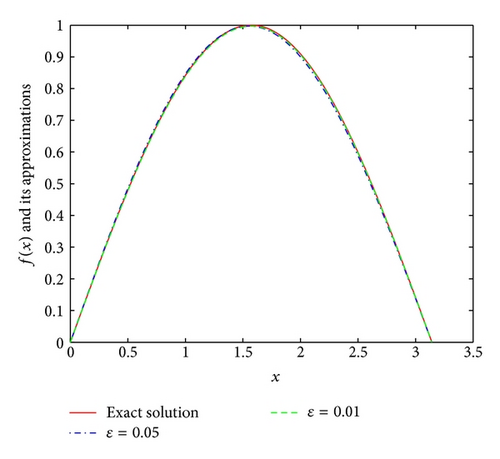
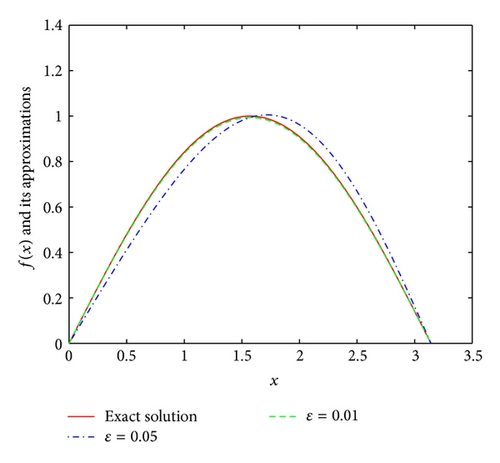
Example 6. It is easy to see that the function u(x, y) = (1 − e−y)sin x and the function f(x) = sinx are the exact solution of the problem (1). Consequently, the data function is g(x) = (1 − e−1)sin x.

Adding a random distributed perturbation to each data function, we obtain vector gδ; that is,

()
where ε indicates the noise level of the measurement data and the function “rand n(·)” generates arrays of random numbers whose elements are normally distributed with mean 0, variance σ2 = 1, and standard deviation σ = 1. “rand n (size(g))” returns an array of random entries that is the same size as g. The bound on the measurement error δ can be measured in the sense of root mean square error (RMSE) according to
()

Using gδ as data function, we obtain the computed approximation fδ,N(x) by (19). The relative error er(f) is given by

()
where ∥·∥2 is defined by (39).

From Figures 1, 2, 3, and 4, we find that the numerical results are quite satisfactory. Even with the noise level up to ε = 0.05, the numerical solutions are still in good agreement with the exact solution. In addition, the numerical results are better with the increase of p at first, but the numerical results are not so good after p = 3. This means that the numerical results are not so good for stronger “smoothness” assumptions on the exact solution f(x) which is consistent with the Tikhonov regularization method in [16]. These results are consistent with [8]. Comparing with [8], we can also easily find that the a posteriori parameter choice rule works better than the a priori parameter choice rule.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
p = 1, M = 200.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
p = 2, M = 200.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
p = 3, M = 200.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
p = 4, M = 200.

6. Conclusions

In this paper, a truncation regularization method is used to identify the unknown source term depending only on the spatial variable for the Poisson equation. The a posteriori rule for choosing regularization parameter with strict theory analysis is presented. In practice, the a priori bound is unknown exactly, and the regularization parameters can not be obtained exactly. This is a defect of the a priori rule for choosing regularization parameter. Using Morozov’s discrepancy principle, we give a posteriori parameter choice rule which depends only on the measured data. For the a posteriori parameter choice rule, we obtain the Hölder type error estimate.

Acknowledgment

The project is supported by the Distinguished Young Scholars Fund of Lanzhou University of Technology (Q201015).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.