Abstract and Applied Analysis
Volume 2013, Issue 1 578942
Research Article
Open Access

A Novel Method for Solving KdV Equation Based on Reproducing Kernel Hilbert Space Method

Mustafa Inc, 

Mustafa Inc

Department of Mathematics, Science Faculty, Firat University, 23119 Elaziğ, Turkey firat.edu.tr

Search for more papers by this author
Ali Akgül, 

Ali Akgül

Department of Mathematics, Education Faculty, Dicle University, 21280 Diyarbakır, Turkey dicle.edu.tr

Search for more papers by this author
Adem Kiliçman, 

Corresponding Author

Adem Kiliçman

Department of Mathematics and Institute for Mathematical Research, University Putra Malaysia (UPM), Selangor, 43400 Serdang, Malaysia upm.edu.my

Search for more papers by this author
First published: 21 February 2013
https://doi.org/10.1155/2013/578942
Citations: 12
Academic Editor: Lan Xu

Abstract

We propose a reproducing kernel method for solving the KdV equation with initial condition based on the reproducing kernel theory. The exact solution is represented in the form of series in the reproducing kernel Hilbert space. Some numerical examples have also been studied to demonstrate the accuracy of the present method. Results of numerical examples show that the presented method is effective.

1. Introduction

In this paper, we consider the Korteweg-de Vries (KdV) equation of the form
()
with initial condition
()
The constant factor ε is just a scaling factor to make solutions easier to describe. Most of the authors chose ε to be one or six. Some mathematicians and physicians investigated the exact solution of the KdV equation without having either initial conditions or boundary conditions [1], while others studied its numerical solution [2, 3].

The numerical solution of KdV equation is of great importance because it is used in the study of nonlinear dispersive waves. This equation is used to describe many important physical phenomena. Some of these studies are the shallow water waves and the ion acoustic plasma waves [4]. It represents the long time evolution of wave phenomena, in which the effect of nonlinear terms uux is counterbalanced by the dispersion uxxx. Thus it has been found to model many wave phenomena such as waves in enharmonic crystals, bubble liquid mixtures, ion acoustic wave, and magnetohydrodynamic waves in a warm plasma as well as shallow water waves [5, 6].

The KdV equation exhibits solutions such as solitary waves, solitons and recurrence [7]. Goda [8] and Vliengenthart [9] used the finite difference method to obtain the numerical solution of KdV equation. Soliman [2] used the collocation solution with septic splines to obtain the solution of the KdV equation. Numerical solutions of KdV equation were obtained by the variational iteration method, finite difference method [3, 10], and by using the meshless based on the collocation with radial basis functions [11]. Wazwaz presented the Adomian decomposition method for KdV equation with different initial conditions [12]. Syam [13] worked the ADM for solving the nonlinear KdV equation with appropriate initial conditions.

In present work, we use the following equation:
()
by transformation for homogeneous initial condition of (1) and (2), we get the following:
()
where
()
In this paper, we solve (1) and (2) by using reproducing kernel method. The nonlinear problem is solved easily and elegantly without linearizing the problem by using RKM. The technique has many advantages over the classical techniques; mainly, it avoids linearization to find analytic and approximate solutions of (1) and (2). It also avoids discretization and provides an efficient numerical solution with high accuracy, minimal calculation, and avoidance of physically unrealistic assumptions. In the next section, we will describe the procedure of this method.

The theory of reproducing kernels was used for the first time at the beginning of the 20th century by Zaremba in his work on boundary value problems for harmonic and biharmonic functions [14]. Reproducing kernel theory has important application in numerical analysis, differential equations, probability and statistics [14, 15]. Recently, using the RKM, some authors discussed fractional differential equation, nonlinear oscillator with discontinuity, singular nonlinear two-point periodic boundary value problems, integral equations, and nonlinear partial differential equations [14, 15].

The efficiency of the method was used by many authors to investigate several scientific applications. Geng and Cui [16] applied the RKHSM to handle the second-order boundary value problems. Yao and Cui [17] and Wang et al. [18] investigated a class of singular boundary value problems by this method and the obtained results were good. Zhou et al. [19] used the RKHSM effectively to solve second-order boundary value problems. In [20], the method was used to solve nonlinear infinite-delay-differential equations. Wang and Chao [21], Li and Cui [22], and Zhou and Cui [23] independently employed the RKHSM to variable-coefficient partial differential equations. Geng and Cui [24] and Du and Cui [25] investigated to the approximate solution of the forced Duffing equation with integral boundary conditions by combining the homotopy perturbation method and the RKHSM. Lv and Cui [26] presented a new algorithm to solve linear fifth-order boundary value problems. In [27, 28], authors developed a new existence proof of solutions for nonlinear boundary value problems. Cui and Du [29] obtained the representation of the exact solution for the nonlinear Volterra-Fredholm integral equations by using the reproducing kernel space. Wu and Li [30] applied iterative reproducing kernel method to obtain the analytical approximate solution of a nonlinear oscillator with discontinuities. Inc et al. [15] used this method for solving Telegraph equation.

The paper is organized as follows. Section 2 introduces several reproducing kernel spaces and a linear operator. The representation in W(Ω) is presented in Section 3. Section 4 provides the main results. The exact and approximate solutions of (1) and (2) and an iterative method are developed for the kind of problems in the reproducing kernel space. We have proved that the approximate solution uniformly converges to the exact solution. Some numerical experiments are illustrated in Section 5. We give some conclusions in Section 6.

2. Preliminaries

2.1. Reproducing Kernel Spaces

In this section, we define some useful reproducing kernel spaces.

Definition 1 (reproducing kernel). Let E be a nonempty abstract set. A function K : E × E → C is a reproducing kernel of the Hilbert space H if and only if

  • (a)

    for all t ∈ E,  K(·, t) ∈ H,

  • (b)

    for all t ∈ E,  φ ∈ H,  〈φ(·), K(·, t)〉 = φ(t). This is also called “the reproducing property”: the value of the function φ at the point t is reproduced by the inner product of φ with K(·, t).

Then we need some notation that we use in the development of the paper. In the next we define several spaces with inner product over those spaces. Thus the space is defined as
()
The inner product and the norm in are defined, respectively, by
()
The space is a reproducing kernel space, that is, for each fixed y ∈ [0,1] and any , there exists a function Ry(x) such that
()
Similarly, we define the space
()
The inner product and the norm in are defined, respectively, by
()
Thus the space is also a reproducing kernel space and its reproducing kernel function rs(t) can be given by
()
and the space
()
where the inner product and and the norm in are defined, respectively, by
()
The space is a reproducing kernel space, and its reproducing kernel function Qy(x) is given by
()
Similarly, the space is defined by
()
The inner product and the norm in are defined, respectively, by
()
The space is a reproducing kernel space and its reproducing kernel function qs(t) is given by
()
Further we define the space W(Ω) as
()
and the inner product and the norm in W(Ω) are defined, respectively, by
()
Now we have the following theorem.

Theorem 2. The space is a complete reproducing kernel space and, its reproducing kernel function Ry(x) can be denoted by

()
where
()

Proof. Since

()
through iterative integrations by parts for (22) we have
()
Note that property of the reproducing kernel
()
If
()
then by (23) we obtain the following equation:
()
when x ≠ y,
()
therefore
()
Since
()
we have
()
()
From (25)–(31), the unknown coefficients ci(y) ve di(y)  (i = 1,2, …, 8) can be obtained. Thus Ry(x) is given by
()

Theorem 3. The W(Ω) is a reproducing kernel space, and its reproducing kernel function is

()
such that for any v(x, t) ∈ W(Ω),
()
where Ry(x),  rs(t) are the reproducing kernel functions of   and , respectively.

Similarly, the space is defined as
()
The inner product and the norm in    are defined, respectively, by
()
Then the space is a reproducing kernel space and its reproducing kernel function G(y,s)(x, t) is
()

3. Solution Representation in W(Ω)

On defining the linear operator as
()
model problem (1) changes to the following problem:
()

Lemma 4. The operator L is a bounded linear operator.

Proof. We have

()
since
()
on using the the continuity of K(x,t)(ξ, η), we have
()
Similarly for i = 0,1,
()
and then
()
Therefore
()

Now, choose a countable dense subset {(x1, t1), (x2, t2), …} in Ω = [0,1] × [0, T] and define
()
where L* is the adjoint operator of L. The orthonormal system of W(Ω) can be derived from the process of Gram-Schmidt orthogonalization of as
()

Theorem 5. Suppose that is dense in Ω; then is complete system in W(Ω) and

()

Proof. We have

()
Clearly Ψi(x, t) ∈ W(Ω). For each fixed v(x, t) ∈ W(Ω), if
()
then
()
Note that is dense in W(Ω), hence, (Lv)(x, t) = 0. It follows that v = 0 from the existence of L−1. So the proof is complete.

Theorem 6. If is dense in Ω, then the solution of (39) is

()

Proof. Since is complete system in W(Ω), we have

()

Now the approximate solution vn(x, t) can be obtained from the n-term intercept of the exact solution v(x, t) and
()
Obviously
()

4. The Method Implementation

If we write
()
then (52) can be written as
()
Now let (x1, t1) = 0; then from the initial conditions of (39), v(x1, t1) is known. We put v0(x1, t1) = v(x1, t1) and define the n-term approximation to v(x, t) by
()
where
()
In the sequel, we verify that the approximate solution vn(x, t) converges to the exact solution, uniformly. First the following lemma is given.

Lemma 7. If  ,  (xn, tn)→(y, s), and f(x, t, v(x, t), vx(x, t)) is continuous, then

()

Proof. Since

()

From the definition of the reproducing kernel, we have

()
It follows that
()
From the convergence of vn−1(x, t), there exists a constant M, such that
()
At the same time, we can prove
()
using Theorem 3. Hence
()
In a similiar way it can be shown that
()
So
()
This completes the proof.

Theorem 8. Suppose that ∥vn∥ is a bounded in (58) and (39) has a unique solution. If      is dense in Ω, then the n-term approximate solution vn(x, t) derived from the above method converges to the analytical solution v(x, t) of (39) and

()
where Bi is given by (59).

Proof. First, we prove the convergence of vn(x, t). From (58), we infer that

()
The orthonormality of   yields that
()
In terms of (71), it holds that ∥vn+1∥ > ∥vn∥. Due to the condition that ∥vn∥ is bounded, ∥vn∥ is convergent and there exists a constant c such that
()
This implies that
()
If m > n, then
()
On account of
()
consequently
()
The completeness of W(Ω) shows that as n → ∞. Now, let we prove that is the solution of (39). Taking limits in (58) we get
()
Note that
()
Therefore
()
In view of (71), we have
()
Since is dense in    Ω, for each (y, s) ∈ Ω, there exists a subsequence such that
()
We know that
()
Let j → ∞; by Lemma 7 and the continuity of f, we have
()
which indicates that satisfy (39). This completes the proof.

Remark 9. In a same manner, it can be proved that

()
where
()
where Bi is given by (59).

5. Numerical Results

In this section, two numerical examples are provided to show the accuracy of the present method. All computations are performed by Maple 16. Results obtained by the method are compared with exact solution and the ADM [13] of each example are found to be in good agreement with each others. The RKM does not require discretization of the variables, that is, time and space, it is not effected by computation round off errors and one is not faced with necessity of large computer memory and time. The accuracy of the RKM for the KdV equation is controllable and absolute errors are very small with present choice of x and t (see Tables 1, 2, 3, and 4 and Figures 1, 2, and 3). The numerical results that we obtained justify the advantage of this methodology.

Table 1. The exact solution of Example 10 for initial condition at 0.1 ≤  x, t  ≤  0.6.
x/t 0.1 0.2 0.3 0.4 0.5 0.6
0.1 1.830273924 1.269479180 0.718402632 0.36141327 0.17121984 0.07882210
0.2 1.922085966 1.423155525 0.839948683 0.43230491 0.20711674 0.09585068
0.3 1.980132581 1.572895466 0.973834722 0.51486639 0.25001974 0.11644607
0.4 2 1.711277572 1.118110335 0.61003999 0.30105415 0.14130164
0.5 1.980132581 1.830273924 1.269479180 0.71840263 0.36141327 0.17121984
0.6 1.922085966 1.922085966 1.423155525 0.83994868 0.43230491 0.20711674
Table 2. The approximate solution of Example 10 for initial condition at 0.1  ≤ x, t  ≤  0.6.
x/t 0.1 0.2 0.3 0.4 0.5 0.6
0.1 1.830273864 1.269478141 0.718402628 0.36141327 0.17128272 0.07883011
0.2 1.922085928 1.423155537 0.839948629 0.43230491 0.20711710 0.09585155
0.3 1.980132606 1.572896076 0.973834717 0.51486633 0.25001974 0.11644677
0.4 2.000000027 1.711278098 1.118110380 0.61004008 0.30105468 0.14130128
0.5 1.980133013 1.830274266 1.269479288 0.71840299 0.36141338 0.17122050
0.6 1.922086667 1.922086057 1.423155510 0.83994874 0.43230465 0.20711669
Table 3. The absolute error of Example 11 for initial condition at 0.1 ≤ x, t ≤ 0.6.
x/t   0.1 0.2 0.3 0.4 0.5 0.6
0.1 1.78 × 10−6 3.01 × 10−9 8.55 × 10−7 3.49 × 10−7 2.85 × 10−7 6.28 × 10−7
0.2 6.38 × 10−7 6.98 × 10−7 6.52 × 10−7 4.51 × 10−7 8.33 × 10−6 2.42 × 10−7
0.3 2.2 × 10−8 9.09 × 10−7 6.88 × 10−6 1.35 × 10−7 2.97 × 10−6 1.69 × 10−7
0.4 1.70 × 10−7 1.03 × 10−7 5.38 × 10−7 1.20 × 10−6 3.98 × 10−7 1.68 × 10−7
0.5 2.26 × 10−7 1.29 × 10−7 8.74 × 10−7 3.13 × 10−7 4.02 × 10−7 9.63 × 10−7
0.6 8.94 × 10−7 7.83 × 10−7 4.34 × 10−7 9.79 × 10−7 2.77 × 10−7 1.45 × 10−8
Table 4. The relative error of Example 11 for initial condition at 0.1 ≤ x, t ≤ 0.6.
x/t 0.1 0.2 0.3 0.4 0.5 0.6
0.1 9.201 × 10−7 5.113 × 10−10 5.707 × 10−7 3.868 × 10−7 6.06 × 10−7 2.76 × 10−6
0.2 3.441 × 10−7 3.498 × 10−7 3.968 × 10−7 4.320 × 10−7 1.48 × 10−6 8.84 × 10−7
0.3 1.255 × 10−8 4.555 × 10−7 3.881 × 10−6 1.132 × 10−7 4.49 × 10−6 5.13 × 10−7
0.4 1.032 × 10−7 5.264 × 10−8 2.862 × 10−7 8.964 × 10−7 5.13 × 10−7 4.27 × 10−7
0.5 1.460 × 10−7 6.857 × 10−8 4.469 × 10−7 2.089 × 10−7 4.44 × 10−7 2.04 × 10−6
0.6 6.079 × 10−7 4.410 × 10−7 2.175 × 10−7 5.958 × 10−7 2.65 × 10−7 2.58 × 10−8
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The absolute error for Example 10 at 0.1 ≤ x,  t ≤ 0.6.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The absolute error for Example 11 at 0.1 ≤ x,  t ≤ 0.6.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The relative error for Example 11 at 0.1 ≤ x,  t ≤ 0.6.

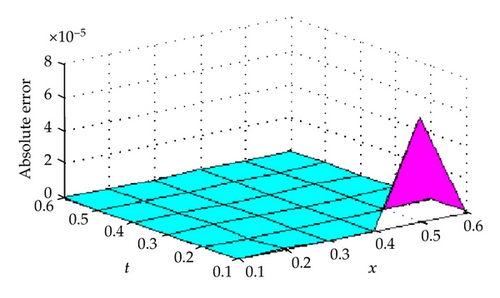
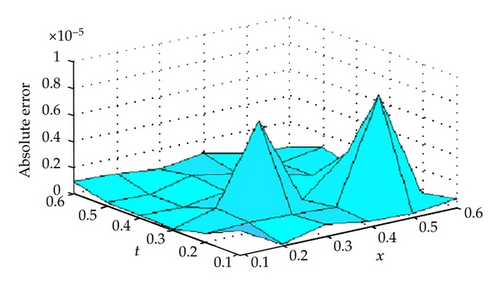
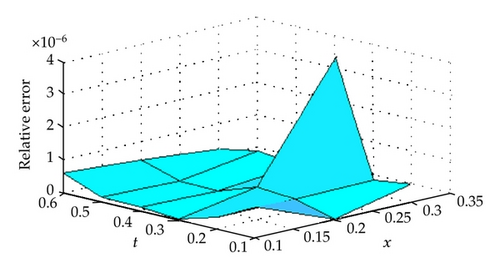
Example 10 (see [13].)Consider the following KdV equation with initial condition

()
with ε = 6. The exact solution is u(x, t) = 2sech2(x − 4t). If we apply (3) to (86), then the following (87) is obtained
()

Example 11 (see [13].)We now consider the KdV equation with initial condition

()
The exact solution is u(x, t) = 12((3 + 4cosh (2x − 8t) + cosh (4x − 64t))/[3cosh (x−28t)+cosh (3x−36t)]2). If we apply (3) to (88), then the following (89) is obtained:
()
Using our method we choose 36 points on [0,1]. We replace v with u for simplicity. In Tables 3 and 4, we compute the absolute errors |u(x, t) − un(x, t)| and the relative errors |u(x, t) − un(x, t)|/|u(x, t)| at the points  {(xi, ti) : xi = ti = i,   i = 0.1, …, 0.6}.

Remark 12. The problem discussed in this paper has been solved with Adomian method [13] and Homotopy analysis method [31]. In these studies, even though the numerical results give good results for large values of x, these methods give away values from the analytical solution for small values of x and t. However, the method is used in our study for large and small values of x and t, results are very close to the analytical solutions can be obtained. In doing so, it is possible to refine the result by increasing the intensive points.

6. Conclusion

In this paper, we introduce an algorithm for solving the KdV equation with initial condition. For illustration purposes, we chose two examples which were selected to show the computational accuracy. It may be concluded that the RKM is very powerful and efficient in finding exact solution for wide classes of problem. The approximate solution obtained by the present method is uniformly convergent.

Clearly, the series solution methodology can be applied to much more complicated nonlinear differential equations and boundary value problems. However, if the problem becomes nonlinear, then the RKM does not require discretization or perturbation and it does not make closure approximation. Results of numerical examples show that the present method is an accurate and reliable analytical method for the KdV equation with initial or boundary conditions.

Acknowledgment

A. Kiliçman gratefully acknowledge that this paper was partially supported by the University Putra Malaysia under the ERGS Grant Scheme having project no. 5527068 and Ministry of Science, Technology and Inovation (MOSTI), Malaysia under the Science Fund 06-01-04-SF1050.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.