Existence and Asymptotic Behavior of Traveling Wave Fronts for a Time-Delayed Degenerate Diffusion Equation

Definition 1. A function φ(ξ) is called a traveling wave front with wave speed c > 0 if there exist ξ_a, ξ_b with −∞ ≤ ξ_a < ξ_b ≤ +∞ such that φ ∈ C²(ξ_a, ξ_b) is monotonic increasing and

or there exist $$, $$ with $$ such that $$ is monotonic decreasing and

• (i)

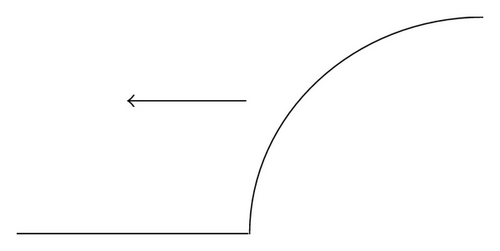
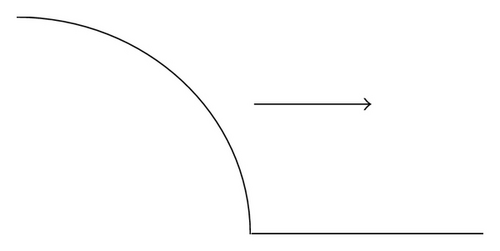
  If ξ_a > −∞ and $$, then φ(ξ) is called an increasing sharp-type traveling wave front (see Figure 1(a)).

• (ii)

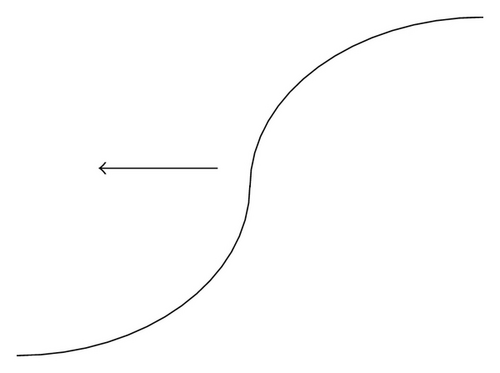
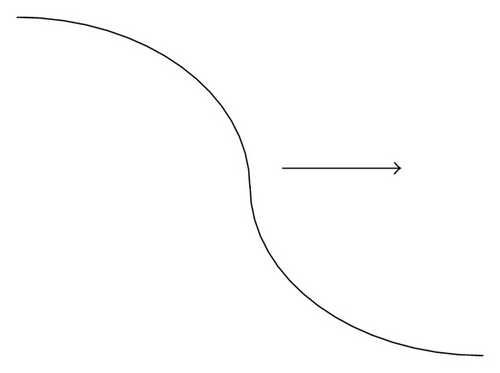
  If ξ_a = −∞ or $$, then φ(ξ) is called an increasing smooth-type traveling wave front (see Figure 2(a)).

•   

  Similarly, we have the following.

• (iii)

  If $$ and $$, then φ(ξ) is called a decreasing sharp-type traveling wave front (see Figure 1(b)).

• (iv)

  If $$ or $$, then φ(ξ) is called a decreasing smooth-type traveling wave front (see Figure 2(b)).

Lemma 2. Assume that 0 < φ₀ < 1 and ψ₁(φ), ψ₂(φ) are solutions of (24) corresponding to different wave speeds c₁,   c₂, respectively, where  ψ₁(φ₀) ≥ ψ₂(φ₀) > 0, ψ₁(φ) > ψ₂(φ) > 0 for 0 < φ < φ₀, and φ₁(ξ₁) =  φ₂(ξ₂) = φ₀. Then, φ₁(ξ₁ − s) < φ₂(ξ₂ − s) if  $$ and φ₁(ξ₁ − s) =  φ₂(ξ₂ − s) =  0 if $$.

Proof. Recalling (19), we see that

where φ_is = φ_i(ξ_i − s),    i = 1,2. The desired conclusion follows immediately.

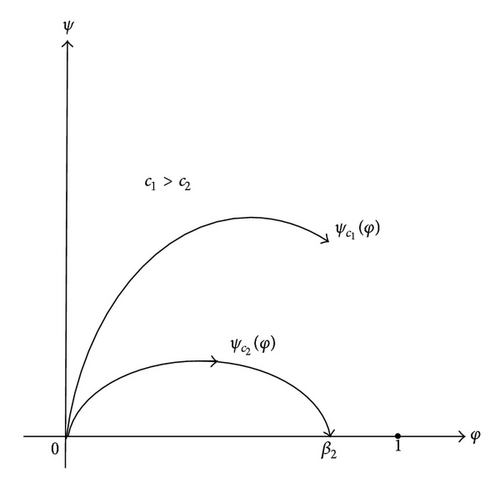
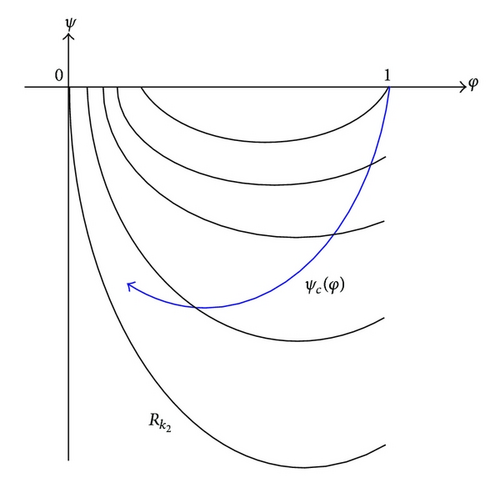
Lemma 3. For any given τ > 0, and c₁ > c₂ ≥ 0, let ψ₁(φ), ψ₂(φ) be solutions of (24) corresponding to c₁, c₂, respectively. Then, ψ₁(φ) > ψ₂(φ) for any φ ∈ (0, β₂), where (0, β₂) is the maximal existence interval of the solution ψ₂(φ) > 0. In addition, ψ₁(β₂) > 0. (See Figure 3(a).)

Proof. We first show that ψ₁(φ) > ψ₂(φ) for sufficiently small φ > 0. The argument consists of three cases, m + p > 2,   m + p = 2, and 1 < m + p < 2.

(i) Consider the case m + p > 2. According to (24), we have

Noticing that φ_cτ ≤ φ, we have for φ ≤ a that Integrating from 0 to φ yields We further have Integrating from 0 to φ gives That is, Therefore, ψ₁(φ) > ψ₂(φ) for sufficiently small φ > 0.

(ii) Consider the case m + p = 2. Similar to (i), we have

and, hence, Consider the sequences {A_n} and {B_n}, where and ε > 0 is sufficiently small. Noticing that A₁ < B₁ and A₁ < A₂, by induction, we obtain For 0 < φ < ε, if then Integrating from 0 to φ yields Thus, we have with A^*(ε) and B^*(ε) satisfying Letting ε → 0, we obtain That is, Therefore, ψ₁(φ) > ψ₂(φ) for sufficiently small φ > 0.

(iii) Consider the case 1 < m + p < 2. Notice that

which means that that is, Consequently, That is, Thus, we have Recalling (46), we see that which implies that On the other hand, by (49), we have and, hence, Summing up, we arrive at which implies that ψ₁(φ) > ψ₂(φ) for sufficiently small φ > 0.

We claim that ψ₁(φ) > ψ₂(φ) for any φ ∈ (0, β₂). Suppose for contradiction that there exists φ₀ ∈ (0, β₂) such that ψ₁(φ₀) = ψ₂(φ₀) = ψ₀ and ψ₁(φ) > ψ₂(φ) for φ ∈ (0, φ₀). Then,

which means that that is, Thus, Denote that φ₁(ξ₁) = φ₂(ξ₂) = φ₀. By Lemma 2, we have which means that $$, a contradiction.

In what follows, we will show that ψ₁(β₂) > 0. Recalling the first equation of (24), we infer that

By Lemma 2, for any φ₁(ξ₁) = φ₂(ξ₂) < β₂, we have since ψ₁ > ψ₂. Thus, we obtain for any φ ∈ (0, β₂). Integrating the previous inequality from φ₀ to φ for any 0 < φ₀ < φ < β₂ yields Letting φ → β₂ gives namely, ψ₁(β₂) > 0. The proof is completed.

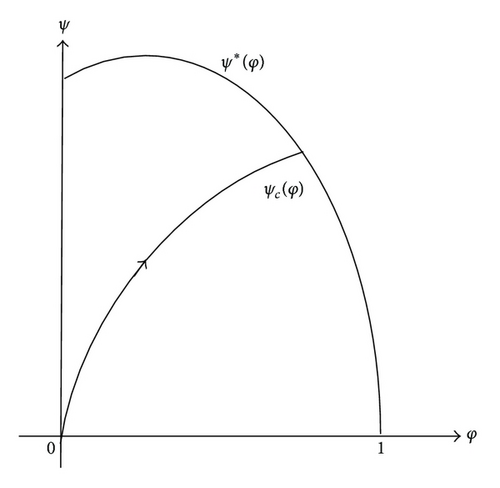
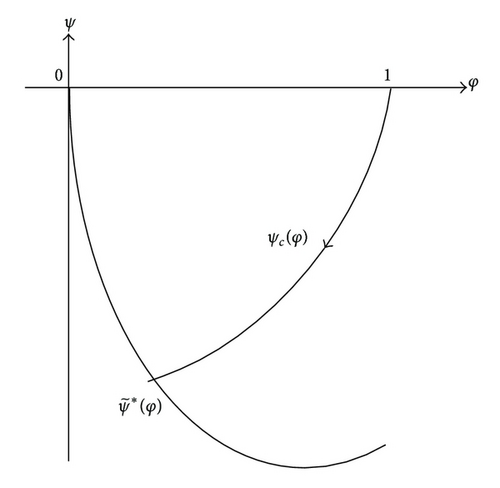
Lemma 4. The trajectory ψ_c(φ) of the problem (24) must intersect with  ψ^*(φ) for sufficiently large c > 0. (See Figure 3(c).)

Proof. For any φ ∈ (0, a], we have φ_cτ ∈ (0, a], and

Let φ₀ ∈ (a, 1) be the first point such that $$. Then, we have Since we have Thus, Denote that Then, for any $$, (74) does not hold and ψ_c(φ) is increasing on (a, 1). Therefore, ψ_c(φ) must intersect with ψ^*(φ) for any $$. The proof is completed.

Theorem 5. (i) If $$, then there is no nontrivial nonnegative solution for problem (23).

(ii) If $$, then there exists a unique $$, such that the problem (23) admits a nonnegative solution ψ(φ), and ψ(φ) > 0 for any φ ∈ (0,1).

Proof. (i) The case $$ has been discussed.

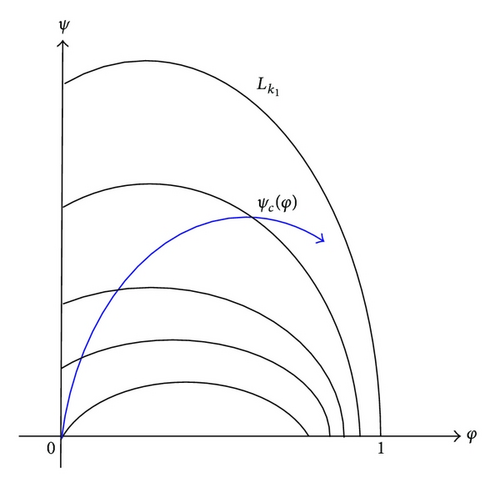
(ii) We know that for any fixed c > 0, (φ, ψ_c) wanders through increasing level sets {L_k} strictly. Thus, (φ, ψ_c) intersects with a level set L_k at most once. Let (σ_c, ϕ_c) be the intersection point of (φ, ψ_c) with $$. Then, if ϕ_c > 0, we have

Define By Lemma 4, $$ is well defined. In what follows, we will show that $$ is just the desired wave speed.

We first have $$. Indeed, when c = 0, the first equation of (24) becomes

Noticing that ψ₀(0⁺) = 0, we have Then, there exists φ₀ ∈ (a, 1) such that since $$. The continuous dependence of ψ_c on c ensures that ψ_c goes to zero before reaching ψ^* for sufficiently small c > 0. Thus, $$.

In addition, by Lemma 3, we know that σ_c is decreasing on c. Assume that

If $$; namely, $$, then by (76), we arrive at So, there exists $$, such that $$. By the continuous dependence of ψ_c on c, there is c > 0 with $$ and close to $$ sufficiently such that ψ_c(φ₁) ≥ ψ^*(φ₁), which implies that ψ_c intersects with  ψ^*. This contradicts the definition of $$. Thus, $$, which implies $$.

Moreover, by Lemma 3, for $$, we have ψ_c(1) > 0. However, if $$, there exists φ_c with a < φ_c < 1 such that ψ_c(φ) → 0 as φ↗φ_c. The proof is completed.

Proposition 6. φ(ξ) is a monotone increasing sharp- or smooth-type traveling wave front of the problem (8)-(9) for some fixed c > 0, if and only if ψ(φ) with ψ(φ) > 0 for any φ ∈ (0,1) is a solution of the problem (23).

Proof. The necessity is clear. Consider the sufficient one. Let ψ(φ) > 0 for any φ ∈ (0,1) be a solution of the problem (23), and φ(ξ) solves

Without loss of generality, let φ(0) = 1/2, and let (α, β) be the maximal existence interval of φ such that 0 < φ < 1. Firstly, we have Moreover, Therefore, if α > −∞ and φ^′(α⁺) ≠ 0, φ(ξ) is a sharp-type traveling wave front; if α = −∞ or φ^′(α⁺) = 0, φ(ξ) is a smooth-type traveling wave front.

Theorem 7. (i) If $$, then there is no increasing traveling wave front for the problem (8)-(9).

(ii) If $$, then there is a unique wave speed $$, such that the problem (8)-(9) admits an increasing traveling wave front.

Theorem 8. Let φ(ξ) be the traveling wave front of the problem (8)-(9) corresponding to the wave speed $$.

• (i)

  If m < 2, then φ(ξ) is a smooth-type traveling wave front.

• (ii)

  If m = 2, then $$ and φ(ξ) is a sharp-type traveling wave front.

• (iii)

  If m > 2, then $$ and φ(ξ) is a sharp-type traveling wave front.

Proof. (i) If 0 < m ≤ 1, it is easy to see that

If 1 < m < 2, from the proof of Lemma 3, we see that when φ > 0 is sufficiently small, Since we have Thus,

(ii) If m = 2, we have

(iii) If m > 2, we have

The proof is completed.

Theorem 9. $$ is nonincreasing in delay τ; namely, if τ₁ > τ₂, then $$.

Proof. Suppose for contradiction that there exist time delays τ₁ and τ₂, with τ₁ > τ₂ and $$. Denote that $$ and  $$ for simplicity. Take c such that

In what follows, denote the solutions of (24) corresponding to wave speed and time delay $$, (c, τ₁), $$ by $$, ψ_c, $$, respectively.

Similar to the proof of Lemma 3, we know that when φ > 0 is sufficiently small, for m + p > 2,

for m + p = 2, for 1 < m + p < 2, Since $$, we have for sufficiently small φ > 0. Furthermore, we claim that $$ for φ ∈ (0,1). Otherwise, there exists φ₀ ∈ (0,1) such that $$ for φ ∈ (0, φ₀), and $$. Then, we have that is, which implies $$. On the other hand, by Lemma 2, we have $$, a contradiction. Similarly, we can get $$. From the uniqueness of wave speed on any fixed τ > 0, this contradicts the definition of $$.

Lemma 10. Let u, v be the solutions of the following problems, respectively:

And let ψ solve the problem (23). Then, ψ(φ) ≤ u(φ) ≤ v(φ) for φ < 1 if ψ, u, v are positive, while v(φ) ≤ ψ(φ) ≤ u(φ) for φ < 1 if ψ, u, v are negative.

Proof. Notice that φ_cτ ≤ φ when ψ is positive, and thus

that is, where Consequently, Integrating from φ to 1 yields and so ψ(φ) ≤ u(φ) if ψ, u > 0. Similarly, u(φ) ≤ v(φ) if u, v > 0.

The proof for ψ, u, v < 0 is similar and omitted here.

Lemma 11. Assume that 0 < φ₀ < 1  and  ψ₁(φ), ψ₂(φ) are solutions of (106) corresponding to different wave speeds c₁, c₂, respectively, where  ψ₁(φ₀) ≤ ψ₂(φ₀) < 0, ψ₁(φ) < ψ₂(φ) < 0 for φ₀ < φ < 1, and φ₁(ξ₁) = φ₂(ξ₂) = φ₀. Then, φ₁(ξ₁ − s) > φ₂(ξ₂ − s) if $$, and φ₁(ξ₁ − s) =  φ₂(ξ₂ − s) = 1 if $$.

Proof. The proof is similar to that of Lemma 2.

Lemma 12. For any given τ > 0, and c₁ > c₂ ≥ 0, let ψ₁(φ), ψ₂(φ) be solutions of (106) corresponding to c₁, c₂, respectively. Then, ψ₁(φ) < ψ₂(φ) for any φ ∈ (α₂, 1), where (α₂, 1) is the maximal existence interval of the solution ψ₂(φ) < 0. In addition, ψ₁(α₂) < 0. (See Figure 4(a).)

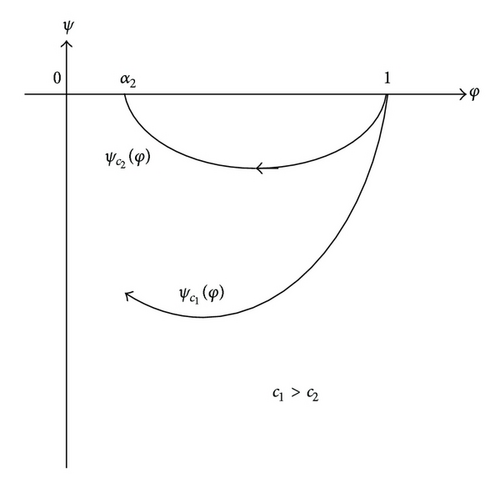
Proof. We first show that ψ₁(φ) < ψ₂(φ) if φ is in a sufficiently small left neighborhood of 1. The argument consists of three cases, q > 1, q = 1, and q < 1.

(i) Consider the case q > 1. According to (106), we have

Noticing that φ_cτ ≥ φ, we have for φ ≥ a that Integrating from φ to 1 yields We further have Integrating from φ to 1 gives Thus, Therefore, ψ₁(φ) < ψ₂(φ) in a left neighborhood of φ = 1.

(ii)   When q = 1, consider the following two systems:

Notice that the right hand side of the previous two systems shares the same Jacobian matrix at (1,0). By a simple calculation, we get the eigenvalues of the matrix P as It is easy to see that (1,0) is a saddle point. And the eigenvector associated with the eigenvalue λ₊ can be We express the local explicit solutions of the problem (114) in the left neighborhood of (1,0) to reach Therefore, near (1,0), we have By the comparison lemma, u₂ ≤ ψ ≤ u₁, which implies Thus, ψ₁(φ) < ψ₂(φ) in a left neighborhood of φ = 1.

(iii) Consider the case 0 < q < 1. Notice that

which means that that is, Consequently, That is, Thus, we have Recalling (123), we see that which implies that On the other hand, by (126), we have and, hence, Summing up, we arrive at which implies that ψ₁(φ) < ψ₂(φ) in a left neighborhood of φ = 1.

The proof for the claims that ψ₁(φ) < ψ₂(φ) for any φ ∈ (α₂, 1) and ψ₁(α₂) < 0 is similar to the proof of Lemma 3 and omitted here.

Lemma 13. The trajectory ψ_c(φ) of the problem (106) must intersect with  $$ for sufficiently large c > 0. (See Figure 4(c).)

Proof. For any φ ∈ [a, 1), we have φ_cτ ∈ [a, 1) and

Let φ₀ ∈ (0, a) be the first point such that $$. Then, we have Since we have Thus, Denote that Then, for any $$, (141) does not hold, and ψ_c(φ) is increasing on (0, a). Therefore, ψ_c(φ) must intersect with  $$ for any $$. The proof is completed.

Theorem 14. (i) If $$, then there is no nontrivial nonpositive solution for the problem (23).

(ii) If $$, then there exists a unique $$, such that the problem (23) admits a nonpositive solution ψ(φ), and ψ(φ) < 0 for any φ ∈ (0,1).

Proof. The proof is similar to that of Theorem 5, and

Proposition 15. φ(ξ) is a monotone decreasing sharp- or smooth-type traveling wave front of the problem (10)-(11) for some fixed c > 0, if and only if ψ(φ) with ψ(φ) < 0 for any φ ∈ (0,1) is a solution of the problem (23).

Proof. The proof is similar to that of Proposition 6.

Theorem 16. (i) If $$, then there is no decreasing traveling wave front for the problem (10)-(11).

(ii) If $$, then there is a unique wave speed $$, such that the problem (10)-(11) admits a decreasing traveling wave front.

Theorem 17. The traveling wave front φ(ξ) of the problem (10)-(11) corresponding to the wave speed $$ obtained earlier is of smooth type.

Proof. It is easy to see that

Thus, Recalling that we know that which means that The proof is completed.

Theorem 18. $$ is nonincreasing in delay τ; namely, if τ₁ > τ₂, then $$.

Proof. The proof is similar to that of Theorem 9.

Theorem 19. Let φ(ξ) be the increasing traveling wave solution of the problem (8)-(9) corresponding to the unique wave speed $$.

• (i)

  If  0 < q < 1, then ξ_b < +∞.

• (ii)

  If q ≥ 1, then ξ_b = +∞. More precisely,

  • (a)

    when q > 1, one has

    $$ ()

  • (b)

    when q = 1, one has

    $$ ()

Proof. (i) For $$, we have $$, and

Consider the following inequality problem: It is easy to prove that ψ(φ) ≥ u(φ) when $$. Now, we construct a function u satisfying (152). Let Then, u satisfies (152) if and only if Take Then, (154) holds when A is appropriately small. Thus, with θ = max {(1 + q)/2, q} and A appropriately small. Since φ(ξ) is the solution of the problem (8)-(9), there exists φ₀ < 1 with 1 − φ₀ small enough such that when φ₀ < φ < 1, When 0 < q < 1,   ξ(φ)<+∞ as φ → 1⁻. Thus, ξ_b < +∞.

(ii) It is easy to see that

Thus, Letting φ → 1, we obtain that is,

For any ε > 0, when φ approaches 1 enough, we have $$. Consider the following two problems:

It is easy to prove that v(φ) ≤ ψ(φ) ≤ u(φ) when φ < 1 with $$. In what follows, we construct two functions u and v satisfying (162) and (163), respectively. Let Then, u satisfies (162) if and only if When q > 1, take When q = 1, take Then, u is a solution of problem (162).

On the other hand, let

Then, v satisfies (163) if and only if When q > 1, take $$; then, (169) is ensured by which holds if Take Then, when (169) holds. When q = 1, take $$, and Then, (169) is ensured.

Summing up, for any φ < 1 with $$, when q > 1,

Noticing that we have that is, When q = 1, A direct calculation gives that is, By the arbitrariness of ε > 0, (149)-(150) hold.

Theorem 20. Let φ(ξ) be the increasing traveling wave solution of the problem (8)-(9) corresponding to the unique wave speed $$.

• (i)

  If m > min {p, 1}, then ξ_a > −∞.

• (ii)

  If m ≤ min {p, 1}, then ξ_a = −∞. More precisely,

  • (a)

    when m + p > 2, if m = 1, one has

    $$ ()

  •  

    and if m < 1, one has

    $$ ()

  • (b)

    when m + p = 2, if m = 1, one has

    $$ ()

  •  

    and if m < 1, one has

    $$ ()

  • (c)

    when 1 < m + p < 2, noticing that m ≤ min {p, 1}, then m ≤ p; if m = p, one has

    $$ ()

  •  

    and if m < p, one has

    $$ ()

Proof. For any φ₀ ∈ (0, a), we see that

From the proof of Lemma 3, we see that when φ > 0 is sufficiently small, where γ = 1 for m + p ≥ 2, and γ = (m + p)/2 for 1 < m + p < 2. It is clear that ξ(φ)→−∞ as φ → 0⁺ if γ ≥ m, and ξ(φ) is finite as φ → 0⁺ if γ < m. That is, if m > min {p, 1}, then ξ_a > −∞; however, if m ≤ min {p, 1}, then ξ_a = −∞. Furthermore, notice that as φ → 0⁺, when m + p > 2, If m = 1, we have If m < 1, When m + p = 2, If m = 1, we have If m < 1, When 1 < m + p < 2, If m = p, we have If m < p, By a simple calculation, (182)–(187) hold.

Theorem 21. Let φ(ξ) be the decreasing traveling wave solution of the problem (10)-(11) corresponding to the unique wave speed $$.

• (i)

  If 0 < q < 1, then $$.

• (ii)

  If q ≥ 1, then $$. More precisely,

  • (a)

    when q > 1, one has

    $$ ()

  • (b)

    when q = 1, one has

    $$ ()

Proof. Let φ₀ approach 1 enough. Then, we have

From the proof of Lemma 12, we see that as φ → 1⁻, where γ = 1 for q ≥ 1, and γ = (q + 1)/2 for 0 < q < 1. It is clear that ξ(φ)→−∞ as φ → 1⁻ if γ ≥ 1, and ξ(φ) is finite as φ → 1⁻ if γ < 1. That is, if 0 < q < 1, then $$; however, if q ≥ 1, then $$. Furthermore, notice that as φ → 1⁻, when q > 1, When q = 1, This yields (199)-(200).

Theorem 22. Let φ(ξ) be the decreasing traveling wave solution of the problem (10)-(11) corresponding to the unique wave speed $$.

• (i)

  If p < min {m, 1}, then $$.

• (ii)

  If p ≥ min {m, 1}, then $$. More precisely,

  • (a)

    when m + p > 2, if p > 1, one has

    $$ ()

  •  

    and if p = 1, one has

    $$ ()

  • (b)

    when m + p = 2, if p > 1, one has

    $$ ()

  •  

    and if p = 1, one has

    $$ ()

  • (c)

    when 1 < m + p < 2, noticing that p ≥ min {m, 1}, then p ≥ m; if p > m, one has

    $$ ()

  •  

    and if p = m, one has

    $$ ()

Proof. (i) For $$, we have $$, and

Consider the following inequality problem: It is easy to prove that ψ(φ) ≤ u(φ) when $$. Now, we construct a function u satisfying (212). Let Then, u satisfies (212) if and only if Take Then, (212) holds when B is appropriately small. Thus, with r = max {(m + p)/2, m + p − 1} and B appropriately small. Since φ(ξ) is the solution of the problem (10)-(11), there exists φ₀ > 0 sufficiently small such that When p < min {m, 1}, ξ(φ)<+∞ as φ → 0⁺. Thus, $$.

(ii) From the proof of Theorem 14, we know that

On the other hand, from the proof of Theorem 17, we also note that By (218)-(219) and it is easy to see that if p ≥ min {m, 1}. That is,

For any 0 < ε < a, when φ approaches 0 enough, we have $$. Consider the following problem:

It is easy to prove that ψ(φ) ≤ u(φ) when φ > 0 with $$. In what follows, we construct a function u satisfying (223). Let Noticing that $$, then u satisfies (223) if When m + p > 2, take r = m + p − 1. Then, (225) is ensured by the following inequalities: Take Then, when $$, (225) holds. Recalling (219), we obtain when $$. When p > 1, we have that is, When p = 1, we have that is, By the arbitrariness of ε > 0, (205)-(206) hold.

When 1 < m + p < 2, take r = (m + p)/2. Then, (225) holds if

Take Then, when (225) holds. Combining with (218), we obtain when $$. When p > m, a simple calculation yields When p = m, By the arbitrariness of ε > 0, (209)-(210) hold.

When m + p = 2, take

Then, (225) holds. On the other hand, consider the following problem: We can see that ψ(φ) ≥ v(φ). Let Then, v satisfies (240). Thus, we conclude that When m < 1, that is, p > 1, When m = 1, that is, p = 1, By the arbitrariness of ε > 0, (207)-(208) hold.