Volume 2013, Issue 1 560804

Research Article

Open Access

Hopf Bifurcation Analysis for a Computer Virus Model with Two Delays

Zizhen Zhang

orcid.org/0000-0002-2879-4434

Key Laboratory of Advanced Process Control for Light Industry, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

School of Management Science and Engineering, Anhui University of Finance and Economics, Bengbu 233030, China aufe.edu.cn

Search for more papers by this author

Huizhong Yang,

Corresponding Author

Huizhong Yang

[email protected]

Key Laboratory of Advanced Process Control for Light Industry, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author

Zizhen Zhang,

Zizhen Zhang

orcid.org/0000-0002-2879-4434

Key Laboratory of Advanced Process Control for Light Industry, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

School of Management Science and Engineering, Anhui University of Finance and Economics, Bengbu 233030, China aufe.edu.cn

Search for more papers by this author

Huizhong Yang,

Corresponding Author

Huizhong Yang

[email protected]

Key Laboratory of Advanced Process Control for Light Industry, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author

First published: 13 November 2013

https://doi.org/10.1155/2013/560804

Citations: 3

Academic Editor: Luca Guerrini

Share a link

Email
Wechat
Bluesky

Abstract

This paper is concerned with a computer virus model with two delays. Its dynamics are studied in terms of local stability and Hopf bifurcation. Sufficient conditions for local stability of the positive equilibrium and existence of the local Hopf bifurcation are obtained by regarding the possible combinations of the two delays as a bifurcation parameter. Furthermore, explicit formulae for determining direction of the Hopf bifurcation and stability of the bifurcating periodic solutions are obtained by using the normal form method and center manifold theory. Finally, some numerical simulations are presented to support the theoretical results.

1. Introduction

Since the pioneering work of Kephart and White [1, 2], many classical epidemic models such as SIR [3–5], SIRS [6–8], SEIR [9, 10], and SEIRS [11, 12], SEIQV [13] have been used to describe the spread of a computer virus in computer network due to the high similarity between computer viruses and biological viruses. In [9], Yuan and Chen proposed the following SEIR model:

(1)

where S(t), E(t), I(t), and R(t) denote the numbers of nodes at time t in states susceptible, exposed, infectious, and recovered, respectively. Yuan and Chen [9] studied the behaviors of virus propagation with the presence of antivirus countermeasures by analyzing the equilibrium stability of system (1).

It is well known that time delays of one or other reasons can cause a stable equilibrium to become unstable and make a system bifurcate periodic solutions and dynamical systems with delay have been studied by many scholars [14–23]. Starting from this point and considering that the antivirus software may use a period to clean the viruses in a computer, Dong et al. [10] proposed the following model with delay:

(2)

where N is the total number of computers in a network. μ describes the impact of quarantine or replacement. ρ_SR describes the impact of implementing real-time immunization. ρ_ER describes the impact of cleaning the virus and immunizing the computers. β is the transmission coefficient. α and γ are the state transition rates. And τ is the period which a computer uses antivirus software to clean viruses. Dong et al. [10] discussed the local stability and existence of local Hopf bifurcation of system (2). Properties of the Hopf bifurcation were also investigated in [10].

However, Yuan and Chen [9] Dong et al. [10] supposed that the recovered computers have a permanent immunization period and can no longer be infected. This is not consistent with real situation. In order to overcome limitation and considering that the recovered computers may be infected again after a temporary immunity period, we investigate the following system with two delays in this paper:

(3)

where τ₁ is the period that a computer uses antivirus software to clean viruses and τ₂ is the temporary immunity period after which a recovered computer may be infected again. ɛ is the transition rate from R to S.

This paper is organized as follows. In Section 2, local stability of the positive equilibrium and the existence of local Hopf bifurcation are discussed. In Section 3, the direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions are determined by using the normal form theory and center manifold theorem. In order to illustrate the validity of the theoretical analysis, some numerical simulations are presented in Section 4. Some main conclusions are drawn in Section 5.

2. Stability and Existence of Local Hopf Bifurcation

In this section, we will study the stability of positive equilibrium and the existence of Hopf bifurcation. It is not difficult to verify if

(4)

system (3) has a unique positive equilibrium D_*(S_*, E_*, I_*, R_*), where

(5)

R₀ is called the basic reproduction number.

Linearizing system (3) at the positive equilibrium D_* yields the following linear system:

(6)

where

(7)

Thus, the characteristic equation of system (3) at D_* is

(8)

where

(9)

Case 1 (τ1 = τ2 = 0). Equation (8) reduces to

(10)

where

(11)

By the Routh-Hurwitz criterion, sufficient conditions for all roots of (10) to have a negative real part are given in the following form:

(12)

Thus, if condition (H₁) (12) holds, then the positive equilibrium D_* is locally asymptotically stable in the absence of delay.

Case 2 (τ1 > 0, τ2 = 0). When τ₁ > 0, τ₂ = 0, (8) becomes the following form:

(13)

where

(14)

Let λ = iω₁ (ω₁ > 0) be the root of (13). Then, we can get

(15)

which follows that

(16)

where

(17)

Let

; then, (16) becomes

(18)

Discussion about the roots of (18) is similar to that in [15]. Therefore, we have the following lemma.

Lemma 1. Let

(19)

Then, for (18), one has the following:

(i)
if e₂₀ < 0, (18) has at least one positive root;
(ii)
if e₂₀ ≥ 0 and α₁ ≥ 0, (18) has positive roots if and only if v₁₁ > 0 and f₁(v₁₁) < 0;
(iii)
if e₂₀ ≥ 0 and α₁ < 0, (18) has positive roots if and only if there exists at least one v_1* ∈ {v₁₁, v₁₂, v₁₃} such that v_1* > 0 and f₁(v_1*) ≤ 0.

In what follows, we assume that (H₂₁): the coefficients in f₁(v₁) satisfy one of the following conditions in (a)–(c):

(a)
e₂₀ < 0;
(b)
e₂₀ ≥ 0, α₁ ≥ 0, v₁₁ > 0, and f₁(v₁₁) < 0;
(c)
e₂₀ ≥ 0, α₁ < 0, and there exists at least one v_1* ∈ {v₁₁, v₁₂, v₁₃} such that v_1* > 0 and f₁(v_1*) ≤ 0.

If (H₂₁) holds, we know that (16) has at least a positive root ω₁₀ such that (13) has a pair of purely imaginary root ±iω₁₀. The corresponding critical value of the delay is

(20)

where

(21)

Differentiating both sides of (13) regarding τ₁, we can obtain

(22)

Thus,

(23)

From (16), we can get

(24)

where

Thus, if condition holds, then the transversality condition is satisfied. According to the Hopf bifurcation theorem in [24], we have the following results.

Theorem 2. Suppose that the conditions (H₂₁)-(H₂₂) hold. Consider

(i)
the positive equilibrium D_*(S_*, E_*, I_*, R_*) of system (3) is asymptotically stable for τ₁ ∈ [0, τ₁₀);
(ii)
system (3) undergoes a Hopf bifurcation at the positive equilibrium D_*(S_*, E_*, I_*, R_*) when τ₁ = τ₁₀ and a family of periodic solutions bifurcate from the positive equilibrium D_*(S_*, E_*, I_*, R_*) near τ₁ = τ₁₀.

Case 3 (τ1 = 0, τ2 > 0). When τ₁ = 0, τ₂ > 0, (8) becomes the following form:

(25)

where

(26)

Let λ = iω₂ (ω₂ > 0) be the root of (25), and we have

(27)

from which, we can obtain

(28)

where

(29)

Let

, then (28) becomes

(30)

Define

(31)

Next, we assume that (H₃₁): the coefficients in f₂(v₂) satisfy one of the following conditions in (a′)–(c′):

(a′)
e₃₀ < 0;
(b′)
e₃₀ ≥ 0, α₂ ≥ 0, v₂₁ > 0, and f₂(v₂₁) < 0;
(c′)
e₃₀ ≥ 0, α₂ < 0, and there exists at least one v_2* ∈ {v₂₁, v₂₂, v₂₃} such that v_2* > 0 and f₂(v_2*) ≤ 0.

According to Lemma 1, we know that if the condition (H₃₁) holds, then (28) has at least a positive root ω₂₀ such that (25) has a pair of purely imaginary roots ±iω₂₀. The corresponding critical value of the delay is

(32)

where

(33)

As in Case 2, we know that if

where

, then

. That is, the transversality condition is satisfied if the condition

holds. Thus, according to the Hopf bifurcation theorem in [24], we have the following results.

Theorem 3. Suppose the conditions (H₃₁)-(H₃₂) hold.

(i)
The positive equilibrium D_*(S_*, E_*, I_*, R_*) of system (3) is asymptotically stable for τ₂ ∈ [0, τ₂₀).
(ii)
System (3) undergoes a Hopf bifurcation at the positive equilibrium D_*(S_*, E_*, I_*, R_*) when τ₂ = τ₂₀ and a family of periodic solutions bifurcate from the positive equilibrium D_*(S_*, E_*, I_*, R_*) near τ₂ = τ₂₀.

Case 4 (τ1 = τ2 = τ > 0). Substituting τ₁ = τ₂ = τ > 0 into (8), then (8) becomes

(34)

where

(35)

Multiplying by e^λτ, (34) becomes

(36)

Let λ = iω (ω > 0) be the root of (36); consider

(37)

which follows that

(38)

where

(39)

As is known, sin²τω + cos ²τω = 1. Thus, we have

(40)

where

(41)

Let ω² = v, then (40) becomes

(42)

In order to give the main results in this paper, we make the following assumption.

(H₄₁) (42) has at least one positive real root.

Suppose that condition (H₄₁) holds. Without loss of generality, we assume that (42) has eight positive real roots, which are denoted as v₁, v₂, …, v₈, respectively. Then (40) has eight positive real roots

. For every fixed ω_k, the corresponding critical value of time delay is

(43)

Define

(44)

Taking the derivative of with respect to (36), it is easy to obtain

(45)

Thus, we have

(46)

where

(47)

Obviously, if condition P_RQ_R + P_IQ_I ≠ 0 holds, then

. Thus, by the Hopf bifurcation theorem in [24], we have the following results.

Theorem 4. Suppose that conditions (H₄₁)-(H₄₂) hold.

(i)
The positive equilibrium D_*(S_*, E_*, I_*, R_*) of system (3) is asymptotically stable for τ ∈ [0, τ₀).
(ii)
System (3) undergoes a Hopf bifurcation at the positive equilibrium D_*(S_*, E_*, I_*, R_*) when τ = τ₀ and a family of periodic solutions bifurcate from the positive equilibrium D_*(S_*, E_*, I_*, R_*) near τ = τ₀.

Case 5 (τ1 > 0, τ2 ∈ (0, τ20)). We consider (8) with τ₂ in its stable interval, regarding τ₁ as a parameter.

Let λ = iω_1* (ω_1* > 0) be the root of (8); we obtain

(48)

where

(49)

We assume that (H₅₁) (48) has at least finite positive roots. And we denote the positive roots of (48) as ω_11*, ω_12*, and ω_1k*. For every fixed ω_1i*, the corresponding critical value of time delay is

(50)

where

(51)

Let

(52)

Next, we make the following assumption:

. Thus, by the Hopf bifurcation theorem in [24], we have the following results.

Theorem 5. Suppose that conditions (H₅₁)-(H₅₂) hold and τ₂ ∈ (0, τ₂₀).

(i)
The positive equilibrium D_*(S_*, E_*, I_*, R_*) of system (3) is asymptotically stable for .
(ii)
System (3) undergoes a Hopf bifurcation at the positive equilibrium D_*(S_*, E_*, I_*, R_*) when and a family of periodic solutions bifurcate from the positive equilibrium D_*(S_*, E_*, I_*, R_*) near .

3. Direction and Stability of the Hopf Bifurcation

In this section, we will investigate the direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions w.r.t. τ₁ for τ₂ ∈ (0, τ₂₀) by using the normal form theory and the center manifold argument in [24]. We assume that where .

Let u₁(t) = S(t) − S_*, u₂(t) = E(t) − E_*, u₃(t) = I(t) − I_*, u₄(t) = R(t) − R_*,

, and normalize t → (t/τ₁). Then system (3) can be transformed into the following form:

(53)

where u_t = (u₁(t), u₂(t), u₃(t), u₄(t)) ^T ∈ C = C([−1,0], R⁴) and

(54)

where

(55)

By the Riesz representation theorem, there exists a 4 × 4 matrix function η(θ, μ):[−1,0] → R⁴ whose elements are of bounded variation such that

(56)

In fact, we choose

(57)

For ϕ ∈ C([−1,0], R⁴), we define

(58)

Then system (53) can be transformed into the following operator equation:

(59)

The adjoint operator A^* of A is defined by

(60)

associated with a bilinear form

(61)

where η(θ) = η(θ, 0).

Let

be the eigenvector of A(0) corresponding to

, and let

be the eigenvector of A^*(0) corresponding to

. From the definition of A(0) and A^*(0), we can get

(62)

From (61), we can get

(63)

Then, we choose

(64)

such that 〈q^*, q〉 = 1,

Next, we can get the coefficients which can be used to determine the direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions by following the algorithms introduced in [24]:

(65)

with

(66)

where E₁ and E₂ can be determined by the following equations respectively

(67)

with

(68)

Therefore, we can calculate the following values:

(69)

Based on the discussion above, we can obtain the following results.

Theorem 6. For system (3), if (), the Hopf bifurcation is supercritical (subcritical). If () the bifurcating periodic solutions are stable (unstable). If (), the period of the bifurcating periodic solutions increases (decreases).

4. Numerical Simulation

In this section, we present some numerical simulations to verify the theoretical analysis in Sections 2 and 3. Let N = 1000, α = 0.1, β = 0.01, γ = 0.08, ɛ = 0.15, μ = 0.01, ρ_SR = 0.2, ρ_ER = 0.2. Then, we can get a particular case of system (3):

(70)

Then, we can get R₀ = 2.5996 > 1 and the unique positive equilibrium D_*(27.9,239.2915,265.8794, 466.9290) of system (70). Further, we have Det₁ = 3.4288 > 0, Det₂ = 5.4964 > 0, Det₃ = 0.6898 > 0, Det₄ = 9.6572e − 004 > 0. That is, condition (H₁) holds.

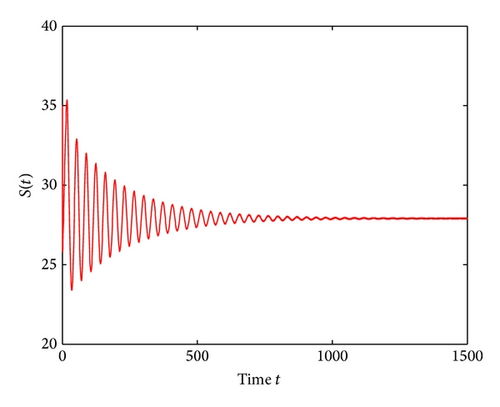
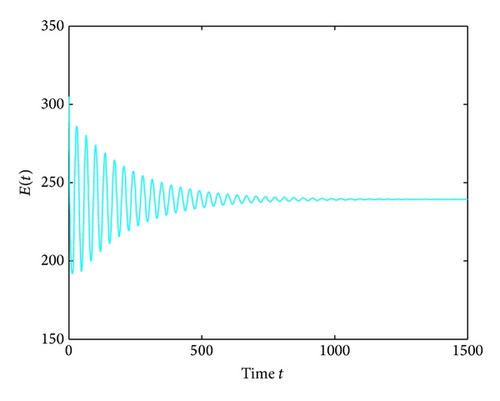
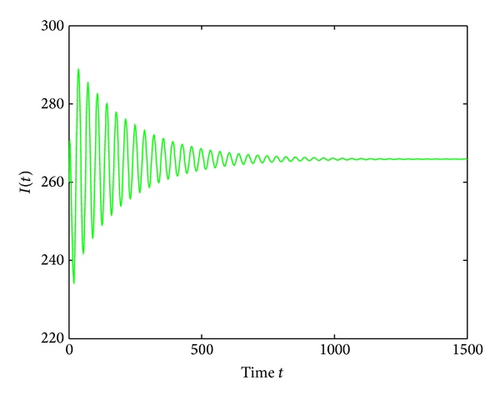
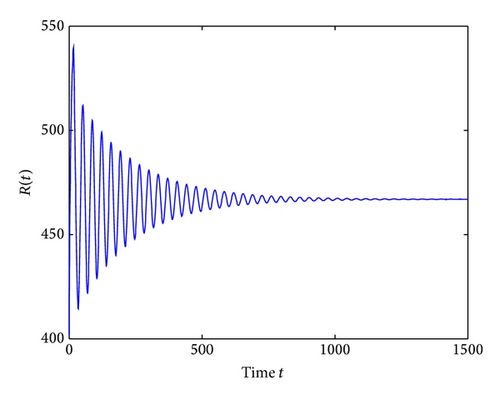
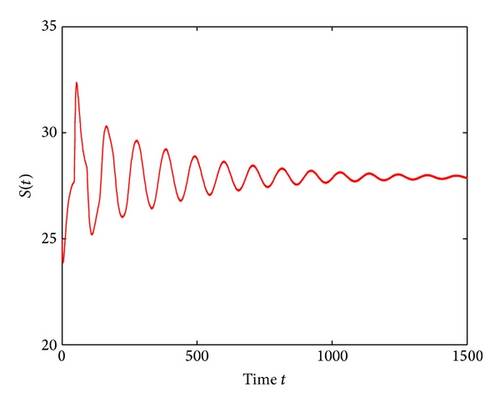
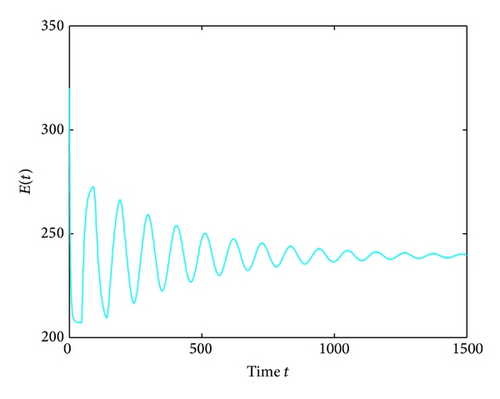
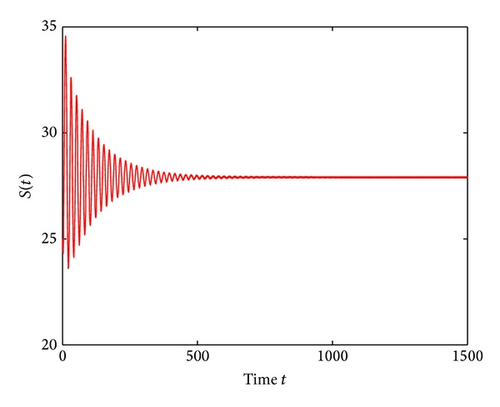
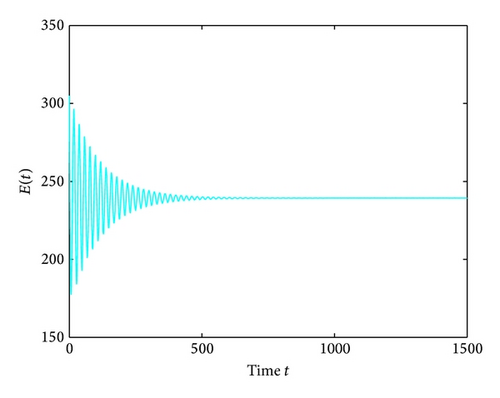
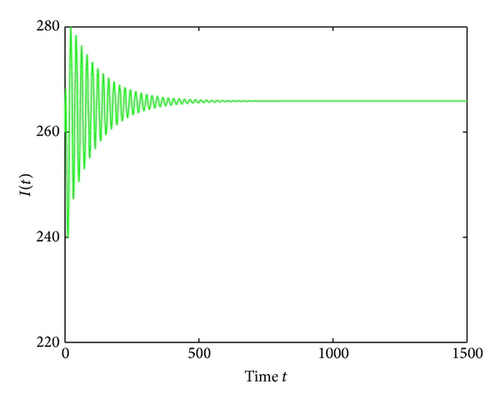
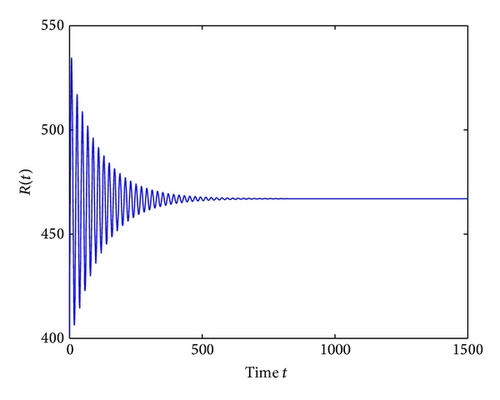
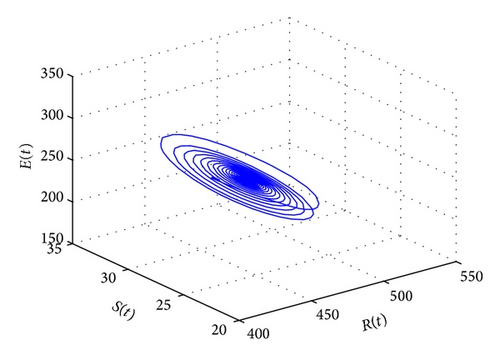
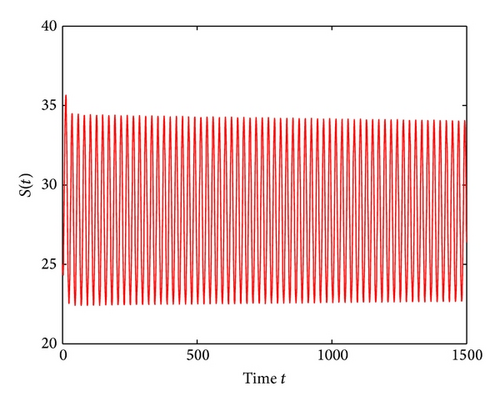
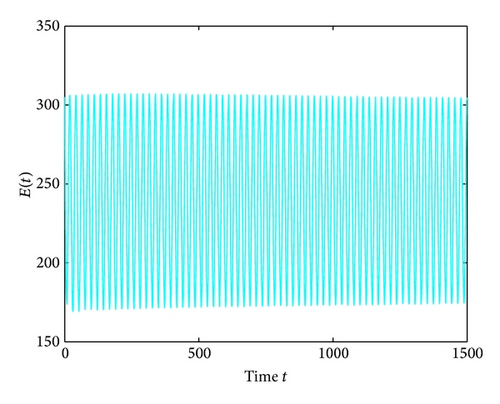
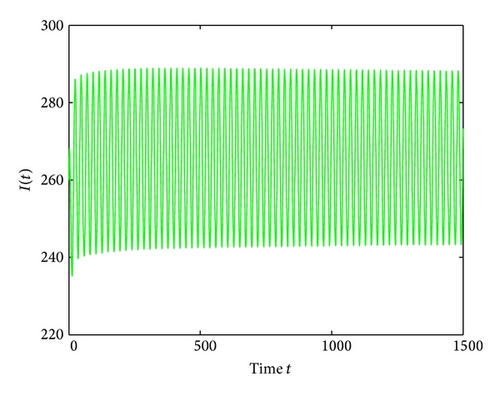
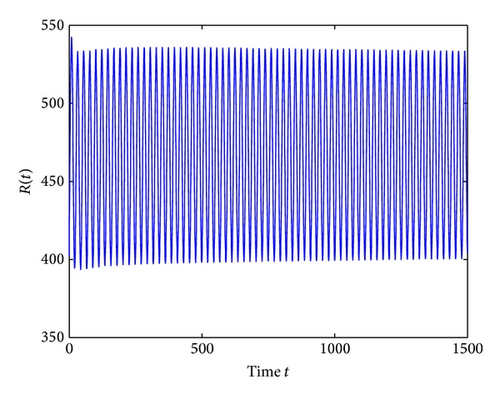
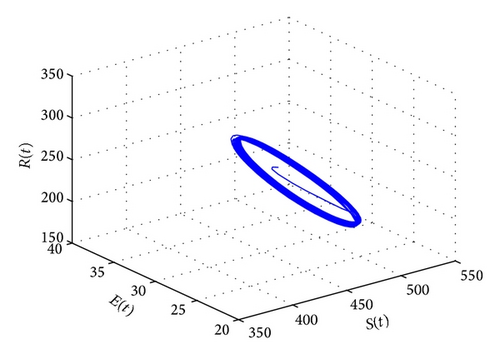
For τ₁ > 0, τ₂ = 0, by some complicated computation, we obtain ω₁₀ = 0.6102, τ₁₀ = 17.2530. By Theorem 2, we know that when τ₁ ∈ [0,17.2530) the positive equilibrium D_* is asymptotically stable which can be illustrated by Figures 1 and 2. However, if we let τ₁ = 20.05 > 17.2530 = τ₁₀, the positive equilibrium D_* becomes unstable and a Hopf bifurcation occurs and a branch of periodic solutions bifurcates from the positive equilibrium D_*. This property can be shown in Figures 3 and 4. Similarly, we have ω₂₀ = 0.1181, τ₂₀ = 52.4927 for τ₁ = 0, τ₂ > 0. The corresponding wave forms and plots are shown in Figures 5, 6, 7, and 8.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The track of the states S, E, I, and R for τ₁ = 15.5000 < 17.2530 = τ₁₀.

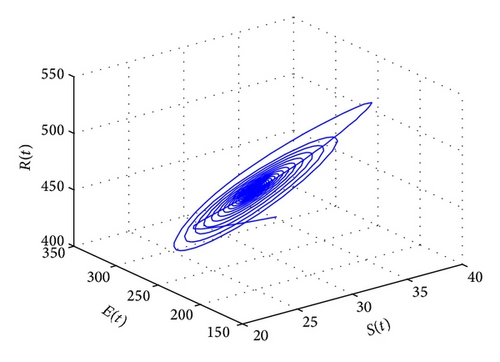
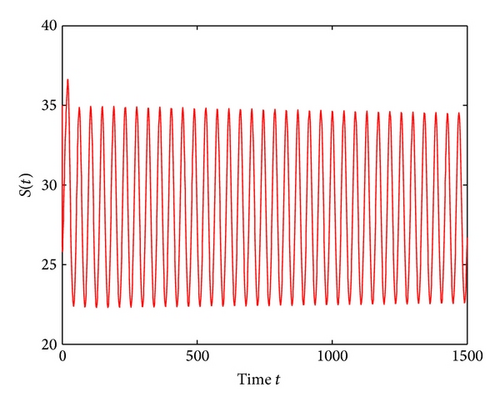
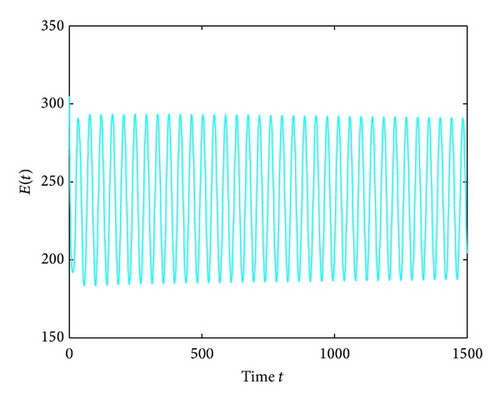
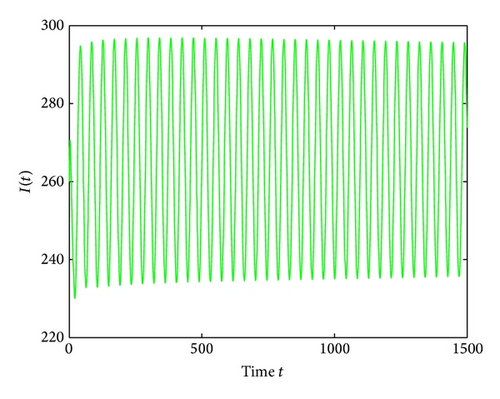
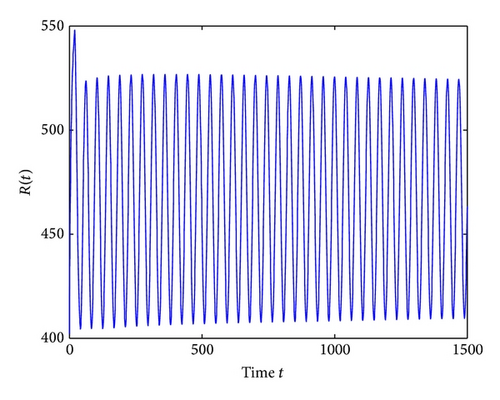
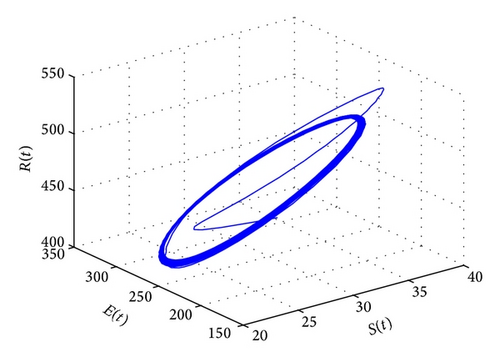
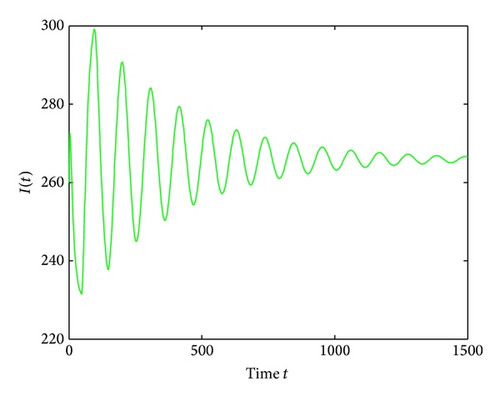
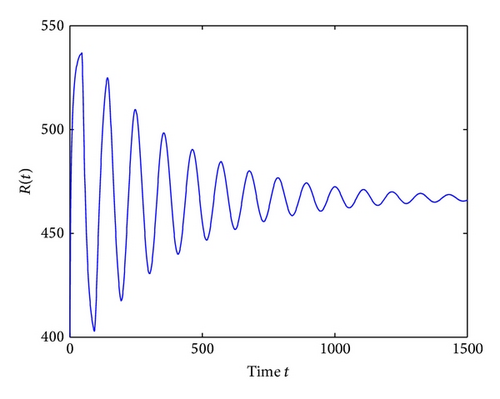
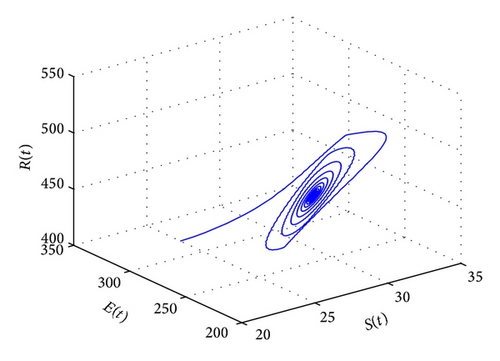
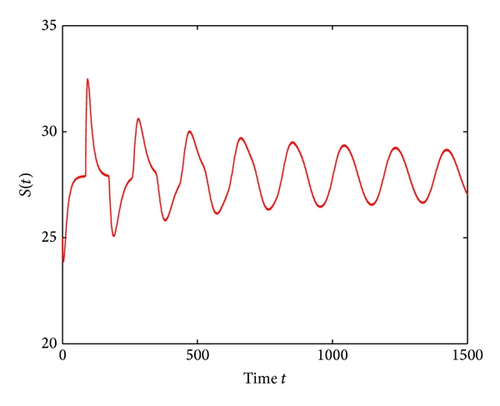
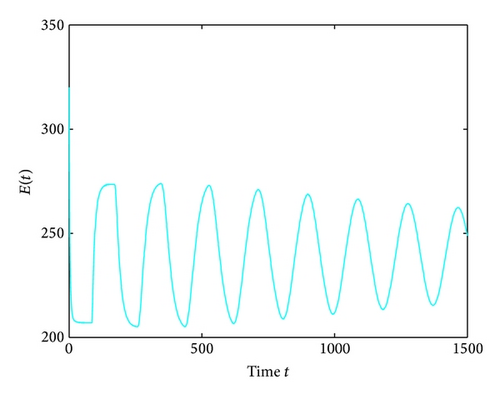
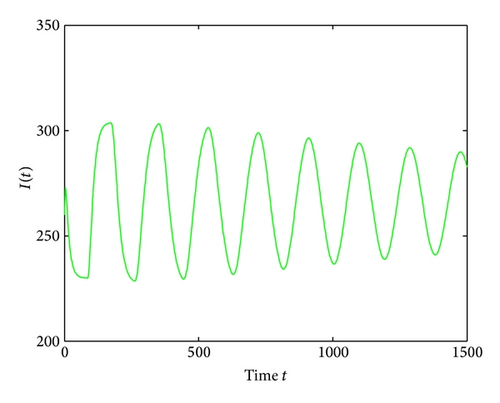
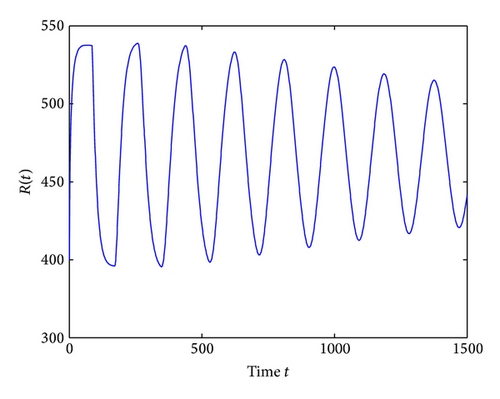
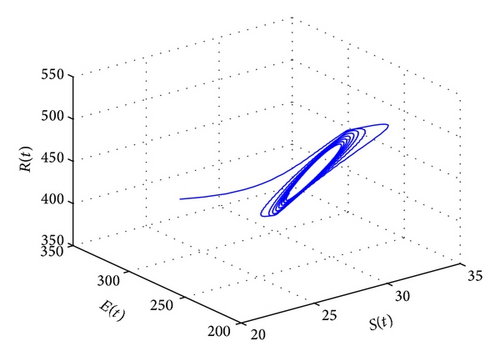
For τ₁ = τ₂ = τ > 0, we get ω₀ = 2.0670, τ₀ = 5.1094. According to Theorem 4, we can conclude that when τ ∈ [0,5.1094), the positive equilibrium D_* is asymptotically stable, which can be seen from Figures 9 and 10. If τ = 5.23 > 5.1094 = τ₀; then, the positive equilibrium D_* becomes unstable, and a branch of bifurcating periodic solutions occurs, which can be shown in Figures 11 and 12.

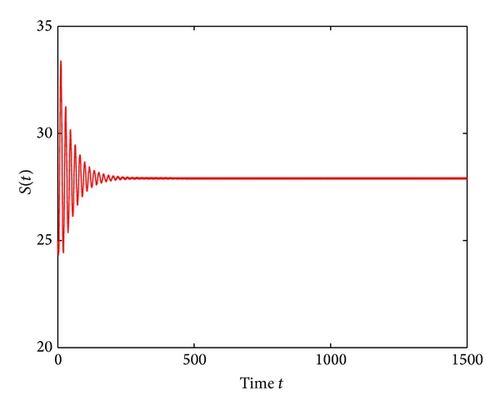
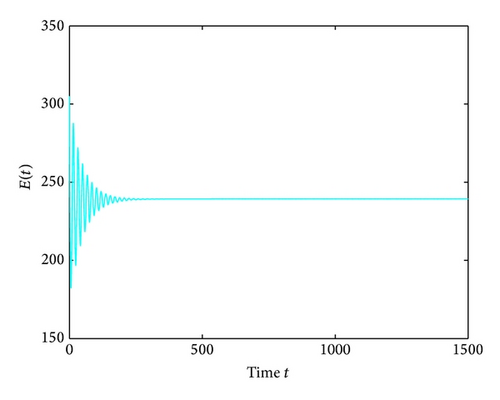
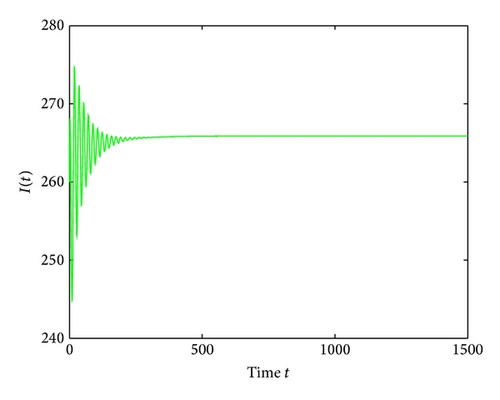
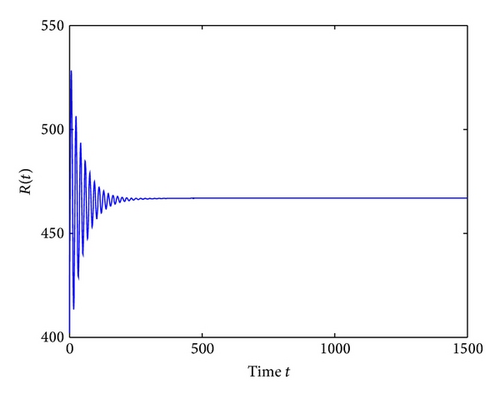
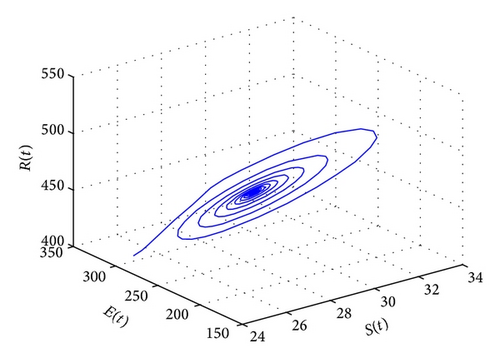
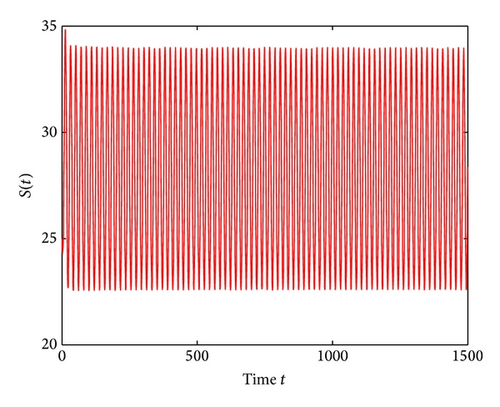
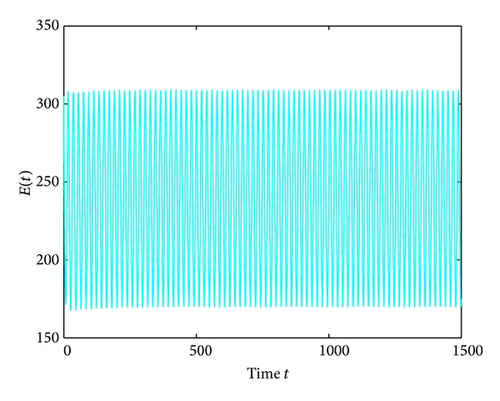
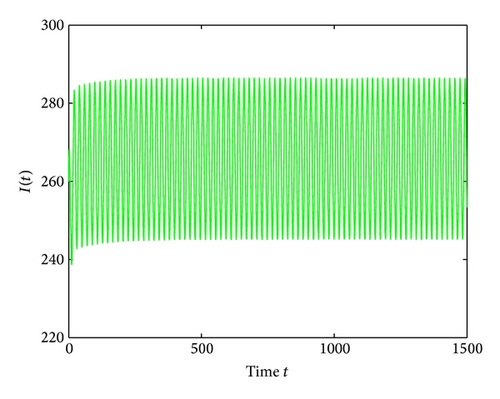
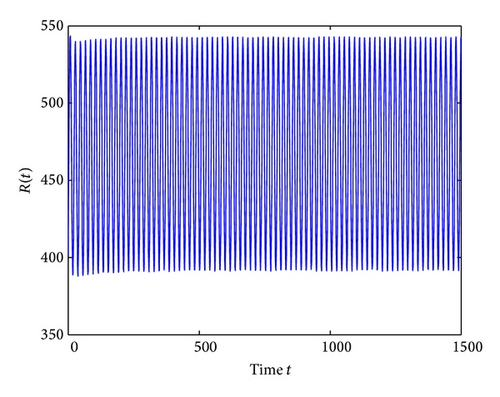
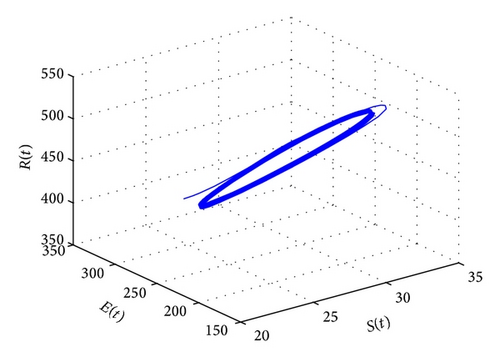
Lastly, we have , for τ₁ > 0, τ₂ = 3 ∈ (0, τ₂₀). The corresponding wave forms and phase plots are shown in Figures 13, 14, 15, and 16. In addition, we have , C₁(0) = −0.2079 − 0.6067i, , , . Thus, by Theorem 6, we can conclude that the Hopf bifurcation is supercritical, the bifurcating periodic solutions are stable, and the period of the periodic solutions increases.

5. Conclusions

Based on the SEIR model considered in the literature [10], we propose an SEIRS model with two delays for the propagation of computer viruses in networks. The effects of the two delays on the dynamics of the model are investigated. It is found that the two delays may lead to local Hopf bifurcation and make the model unstable under some certain conditions. When the corresponding delay is suitable and small, the positive equilibrium is asymptotically stable. In this case, the propagation of computer viruses can be predicted and controlled. However, a local Hopf bifurcation occurs and a branch of periodic solutions bifurcates from the positive equilibrium when the corresponding delay passes though a critical value. In such conditions, propagation of the computer viruses is out of control. This phenomenon is not welcome in networks. Therefore, In order to control and even eliminate the propagation of computer viruses, the two delays τ₁ and τ₂ in the model should remain less than the corresponding critical value. Furthermore, by using the normal form theory and center manifold theorem, the properties of the Hopf bifurcation such as direction and stability are determined. Some numerical simulations are also included to testify the theoretical analysis.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this article.

Acknowledgment

This work was supported by the National Natural Science Foundation of China (61273070), a project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.

References

1 Kephart J. O. and White S. R., Directed-graph epidemiological models of computer viruses, Proceedings of the IEEE Computer Society Symposium on Research in Security and Privacy, May 1991, 343–359, 2-s2.0-0026156688.
Google Scholar
2 Kephart J. O. and White S. R., Measuring and modeling computer virus prevalence, Proceedings of the IEEE Computer Society Symposium on Research in Security and Privacy, May 1993, 2–15, 2-s2.0-0027150413.
Google Scholar
3 Wierman J. C. and Marchette D. J., Modeling computer virus prevalence with a susceptible-infected-susceptible model with reintroduction, Computational Statistics & Data Analysis. (2004) 45, no. 1, 3–23, https://doi.org/10.1016/S0167-9473(03)00113-0, MR2041255, ZBL05373937.
10.1016/S0167-9473(03)00113-0
Web of Science® Google Scholar
4 Mishra B. K. and Jha N., Fixed period of temporary immunity after run of anti-malicious software on computer nodes, Applied Mathematics and Computation. (2007) 190, no. 2, 1207–1212, 2-s2.0-34250656571, https://doi.org/10.1016/j.amc.2007.02.004.
10.1016/j.amc.2007.02.004
Web of Science® Google Scholar
5 Piqueira J. R. C. and Araujo V. O., A modified epidemiological model for computer viruses, Applied Mathematics and Computation. (2009) 213, no. 2, 355–360, https://doi.org/10.1016/j.amc.2009.03.023, MR2536658, ZBL1185.68133.
10.1016/j.amc.2009.03.023
Web of Science® Google Scholar
6 Han X. and Tan Q. L., Dynamical behavior of computer virus on internet, Applied Mathematics and Computation. (2010) 217, no. 6, 2520–2526, https://doi.org/10.1016/j.amc.2010.07.064, MR2733695, ZBL1209.68139.
10.1016/j.amc.2010.07.064
Web of Science® Google Scholar
7 Ren J. G., Yang X. F., Yang L.-X., Xu Y., and Yang F., A delayed computer virus propagation model and its dynamics, Chaos, Solitons & Fractals. (2012) 45, no. 1, 74–79, https://doi.org/10.1016/j.chaos.2011.10.003, MR2863589, ZBL06196114.
10.1016/j.chaos.2011.10.003
Web of Science® Google Scholar
8 Ren J. G., Yang X. F., Zhu Q., Yang L.-X., and Zhang C., A novel computer virus model and its dynamics, Nonlinear Analysis. Real World Applications. (2012) 13, no. 1, 376–384, https://doi.org/10.1016/j.nonrwa.2011.07.048, MR2846848, ZBL1238.34076.
10.1016/j.nonrwa.2011.07.048
Web of Science® Google Scholar
9 Yuan H. and Chen G., Network virus-epidemic model with the point-to-group information propagation, Applied Mathematics and Computation. (2008) 206, no. 1, 357–367, https://doi.org/10.1016/j.amc.2008.09.025, MR2474981, ZBL1162.68404.
10.1016/j.amc.2008.09.025
Web of Science® Google Scholar
10 Dong T., Liao X. F., and Li H. Q., Stability and Hopf bifurcation in a computer virus model with multistate antivirus, Abstract and Applied Analysis. (2012) 2012, 16, 841987, https://doi.org/10.1155/2012/841987, MR2910735, ZBL1237.37067.
10.1155/2012/841987
Google Scholar
11 Mishra B. K. and Saini D. K., SEIRS epidemic model with delay for transmission of malicious objects in computer network, Applied Mathematics and Computation. (2007) 188, no. 2, 1476–1482, https://doi.org/10.1016/j.amc.2006.11.012, MR2335644, ZBL1118.68014.
10.1016/j.amc.2006.11.012
Web of Science® Google Scholar
12 Mishra B. K. and Pandey S. K., Dynamic model of worms with vertical transmission in computer network, Applied Mathematics and Computation. (2011) 217, no. 21, 8438–8446, https://doi.org/10.1016/j.amc.2011.03.041, MR2802253, ZBL1219.68080.
10.1016/j.amc.2011.03.041
Web of Science® Google Scholar
13 Wang F. W., Zhang Y. K., Wang C. G., Ma J., and Moon S., Stability analysis of a SEIQV epidemic model for rapid spreading worms, Computers and Security. (2010) 29, no. 4, 410–418, 2-s2.0-77951206095, https://doi.org/10.1016/j.cose.2009.10.002.
10.1016/j.cose.2009.10.002
PubMed Web of Science® Google Scholar
14 Yao Y., Xie X.-W., Guo H., Yu G., Gao F.-X., and Tong X.-J., Hopf bifurcation in an Internet worm propagation model with time delay in quarantine, Mathematical and Computer Modelling. (2013) 57, 2635–2646, 2-s2.0-79960561776, https://doi.org/10.1016/j.mcm.2011.06.044.
10.1016/j.mcm.2011.06.044
Google Scholar
15 Zhang T. L., Liu J. L., and Teng Z. D., Stability of Hopf bifurcation of a delayed SIRS epidemic model with stage structure, Nonlinear Analysis. Real World Applications. (2010) 11, no. 1, 293–306, https://doi.org/10.1016/j.nonrwa.2008.10.059, MR2570549, ZBL1195.34130.
10.1016/j.nonrwa.2008.10.059
Web of Science® Google Scholar
16 Gakkhar S. and Singh A., Complex dynamics in a prey predator system with multiple delays, Communications in Nonlinear Science and Numerical Simulation. (2012) 17, no. 2, 914–929, https://doi.org/10.1016/j.cnsns.2011.05.047, MR2834461, ZBL1243.92051.
10.1016/j.cnsns.2011.05.047
Web of Science® Google Scholar
17 Meng X.-Y., Huo H.-F., and Xiang H., Hopf bifurcation in a three-species system with delays, Journal of Applied Mathematics and Computing. (2011) 35, no. 1-2, 635–661, https://doi.org/10.1007/s12190-010-0383-x, MR2748391, ZBL1209.92058.
10.1007/s12190-010-0383-x
Google Scholar
18 Kar T. K. and Ghorai A., Dynamic behaviour of a delayed predator-prey model with harvesting, Applied Mathematics and Computation. (2011) 217, no. 22, 9085–9104, https://doi.org/10.1016/j.amc.2011.03.126, MR2803972, ZBL1215.92065.
10.1016/j.amc.2011.03.126
Web of Science® Google Scholar
19 Zhang J.-F., Bifurcation analysis of a modified Holling-Tanner predator-prey model with time delay, Applied Mathematical Modelling. (2012) 36, no. 3, 1219–1231, https://doi.org/10.1016/j.apm.2011.07.071, MR2872892, ZBL1243.34119.
10.1016/j.apm.2011.07.071
Web of Science® Google Scholar
20 Guo S. and Jiang W., Global stability and Hopf bifurcation for Gause-type predator-prey system, Journal of Applied Mathematics. (2012) 2012, 17, 260798, https://doi.org/10.1155/2012/260798, MR2904519, ZBL1248.34125.
10.1155/2012/260798
Google Scholar
21 Jana S. and Kar T. K., Modeling and analysis of a prey-predator system with disease in the prey, Chaos, Solitons & Fractals. (2013) 47, 42–53, https://doi.org/10.1016/j.chaos.2012.12.002, MR3021823, ZBL1258.92038.
10.1016/j.chaos.2012.12.002
Web of Science® Google Scholar
22 Xu C. J. and He X. F., Stability and bifurcation analysis in a class of two-neuron networks with resonant bilinear terms, Abstract and Applied Analysis. (2011) 2011, 21, 697630, https://doi.org/10.1155/2011/697630, MR2802842, ZBL1218.37122.
10.1155/2011/697630
Google Scholar
23 Li Y. K. and Li C. Z., Stability and Hopf bifurcation analysis on a delayed Leslie-Gower predator-prey system incorporating a prey refuge, Applied Mathematics and Computation. (2013) 219, no. 9, 4576–4589, https://doi.org/10.1016/j.amc.2012.10.069, MR3001507.
10.1016/j.amc.2012.10.069
Web of Science® Google Scholar
24 Hassard B. D., Kazarinoff N. D., and Wan Y. H., Theory and Applications of Hopf Bifurcation, 1981, Cambridge University Press, Cambridge, UK.
Google Scholar

Citing Literature

All articles

Hopf Bifurcation Analysis for a Computer Virus Model with Two Delays

Abstract

1. Introduction

2. Stability and Existence of Local Hopf Bifurcation

3. Direction and Stability of the Hopf Bifurcation

4. Numerical Simulation

5. Conclusions

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Hopf Bifurcation Analysis for a Computer Virus Model with Two Delays

Abstract

1. Introduction

2. Stability and Existence of Local Hopf Bifurcation

3. Direction and Stability of the Hopf Bifurcation

4. Numerical Simulation

5. Conclusions

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Related

Information