Sliding Mode Extremum Seeking Control Scheme Based on PSO for Maximum Power Point Tracking in Photovoltaic Systems

1. Introduction

With the gradual depletion of the world’s supply of natural resources and mounting concern regarding the greenhouse effect and global warming, the need has emerged for new energy sources capable of meeting the world’s power needs in a sustainable and environmentally friendly manner. In response to this requirement, many green energy sources have been proposed in recent decades, including photovoltaic power generation systems, wind farms, hydraulic power generation systems, fuel cells, and biomass energy generation systems. Among these various energy sources, photovoltaic power generation systems are particularly attractive since they have a simple architecture, high reliability, and an easily extendable generating capacity. However, the performance of photovoltaic modules is highly sensitive to the angle of the incident sunlight, the atmospheric temperature, the solar panel conversion efficiency, and so on. Therefore, to maximize the system efficiency and robustness toward environmental perturbations and changes in the irradiance conditions, effective control schemes are required [1, 2].

The literature contains many proposals for maximum power point tracking (MPPT) schemes in photovoltaic systems. For example, Femia et al. [3] proposed a perturbation and observation (P&O) method in which the output voltage of each photovoltaic module was adjusted by increasing or reducing the load in accordance with observations of the output power before and after loading, respectively. However, in the proposed approach, the point of maximum power is reached via a process of successive adjustment, and thus poor stability, energy loss, and a low generating efficiency inevitably occur. Abdelsalam et al. [4] proposed an improved P&O scheme for MPP tracking in photovoltaic systems and showed that the proposed approach reduced oscillations during the tracking process and improved both the efficiency and the reliability of the overall power grid. Li and Wang [5] proposed an incremental conductance (IC) method in which the output voltage of each solar cell was increased or decreased depending on whether the output power of the cell was located to the left or the right of the MPP (dP/dV = 0), respectively. However, the performance of the proposed method is dependent on a highly precise measurement of the output power, which is not easily achieved in practical implementations. Safari and Mekhilef [6] presented an improved IC method for solving the MPPT problem based on a direct control scheme. The experimental results showed that the proposed method enabled the MPP to be tracked rapidly and without excessive oscillation. Liu et al. [7] proposed an incremental MPPT algorithm in which the step size was adjusted automatically in accordance with changes in the voltage output of the photovoltaic modules. The experimental results showed that the proposed method improved both the speed and the accuracy of the MPPT process compared to a conventional fixed step size method. However, the method has poor robustness toward sudden changes in the irradiance conditions and leads to significant energy losses as a result. Koutroulis et al. [8] presented an MPPT control system consisting of a buck-type DC-DC converter regulated by a microcontroller. In the proposed approach, the DC-DC converter was adjusted directly in accordance with the output power of the photovoltaic array, thereby reducing the complexity of the system. However, the efficiency of the proposed approach is highly sensitive to the measurement accuracy of the power signal. The authors in [9–11] proposed various extremum seeking control (ESC) techniques for solving the MPPT problem in photovoltaic systems. Compared to conventional adaptive control methods, which process only a given or present reference trajectory, ESC methods require no modeling and result in a more precise control performance. The output characteristic curve of a photovoltaic power generation system has a nonlinear form. Thus, conventional MPPT algorithms commonly converge toward a local MPP rather than the global MPP. It was shown in [12, 13] that ESC schemes provide an effective means of resolving this problem, thereby minimizing energy losses and ensuring the stability and robustness of the system.

Brunton et al. [13] presented a novel ESC algorithm based on a natural inverter ripple for MPP tracking in solar power systems. The experimental results showed that the proposed system was capable of tracking the MPP with an accuracy of more than 99% within a very short time. However, the proposed method has poor robustness and therefore suffers a severe performance loss given rapid changes in the irradiance conditions.

The present study proposes an enhanced ESC control scheme for solving the MPPT problem in photovoltaic systems. In the proposed approach, the robustness of the MPPT algorithm toward irradiance changes is enhanced by means of a sliding mode control (SMC) law [14]. Furthermore, the chattering phenomenon observed in traditional MPPT schemes is suppressed by means of a sliding layer concept. Finally, the response time and stability of the proposed controller are enhanced by using a particle swarm optimization (PSO) algorithm to determine the optimal value of the gain constant (U₀). It is shown that the proposed method outperforms traditional MPPT schemes based on gradient detection methods in terms of a better transient response, an improved steady-state stability, and an improved robustness.

The remainder of this paper is organized as follows. Section 2 describes the application of the ESC technique to the MPPT problem and introduces the Sliding Mode ESC (SMESC) scheme proposed in the present study. Section 3 introduces the concept of PSO. Section 4 describes the system circuit architecture. Section 5 presents and discusses the experimental and numerical results. Finally, Section 6 provides some brief concluding remarks.

2. ESC Technology and SMESC Controller Design

2.1. Extremum Seeking Control (ESC) Scheme

Figure 1 presents a block diagram of a general ESC scheme. As shown, the major components comprise an integrator, a differentiator, a logic circuit, and an integral gain constant. In the present study, the aim of the ESC control scheme is to determine the global maximum value of the x-y curve, (i.e., the P-V curve of the photovoltaic system).

According to Figure 1,

$$ ()

where ε = ±1 and K is a positive constant. Furthermore,

$$ ()

If g < 0, then ε = −1. Conversely, if g > 0, then ε = 1.

Figure 2 shows the dx/dt and dy/dt signal changes corresponding to momenta a, b, c, and d, respectively [15]. Note that in the present study,  dx/dt, and dy/dt correspond to the rates of change of the voltage and the power, respectively. Since (dy/dx) = (dy/dt)/(dx/dt), it follows that

$$ ()

$$ ()

where sign () is a sign function.

According to (4), the balance point dy/dx = 0 corresponds to the extremum of the x-y curve in Figure 2. Moreover, system dynamics expressed in (4) depend on the slope of the x-y curve. As shown in the following, the stability of the balance point can be confirmed by means of the Lyapunov theorem. Let the Lyapunov function be specified as follows:

$$ ()

Differentiating (5) with respect to time yields

$$ ()

According to Figure 2,

$$ ()

Therefore, selecting a positive value of K yields $$. Thus, the stability of the balance point is confirmed.

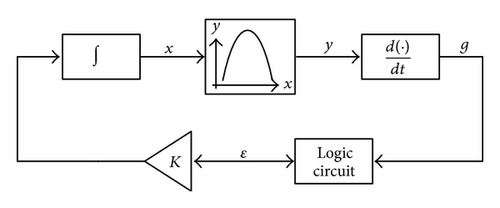
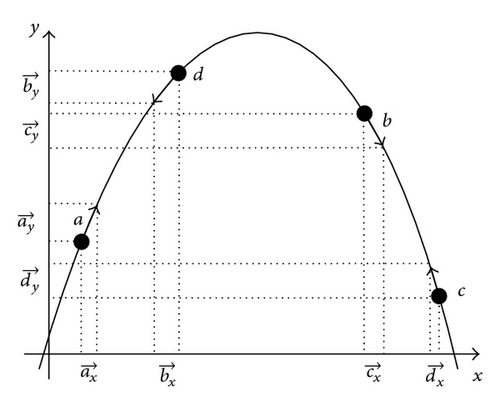
2.2. Sliding Mode Extremum Seeking Control (SMESC) Scheme

As shown in Figure 3, the robustness and stability of the ESC scheme used to solve the MPPT problem is enhanced in this study by adopting a sliding control law [16]. The stability of the resulting Sliding Mode ESC (SMESC) scheme is demonstrated in the following discussions.

In accordance with conventional control theory, the sliding surface in Figure 3 is defined as

$$ ()

According to Figure 3,

$$ ()

$$ ()

where Z₀ and U₀ are both constants and ρ is the maximum value of y (power) versus x (voltage). In photovoltaic system, ρ can be obtained in advance after the irradiance was measured correctly. In this study, it is assumed that the irradiance can be measured correctly at any time.

Equation (9) can be replaced by

$$ ()

To ensure the stability of the MPPT system, Z₀ must be far larger than both U₀ and ρ, that is,

$$ ()

To demonstrate the stability of the proposed SMESC scheme, let the Lyapunov function be defined as

$$ ()

Differentiating (13) with respect to time t yields

$$ ()

where ρ is the maximum power of each solar panel in the photovoltaic array and is a given value, and dy/dx approaches zero close to the maximum power point (MPP). Therefore, if Z₀ ≫ U₀ and Z₀ ≫ ρ, selecting appropriate values of Z₀ and U₀ yield the condition

$$ ()

Thus, the stability of the proposed SMESC scheme is confirmed.

The ESC and SMESC schemes presented in Figures 1 and 3, respectively, both use the sign function sign () to determine whether or not to change the signal. In theory, realizing an ideal switching function sign (σ) requires an infinitely high switching frequency. Such a switching frequency cannot be achieved in real-world systems. Thus, the switching function is generally achieved using ultrahigh speed switching components instead. However, the continuous jumping of the system trajectory to the minimal space on either side of the sliding mode (σ = 0) results in high-frequency noise (chatter), which degrades the tracking performance of the MPPT controller and leads to energy losses. Amongst the various techniques available for suppressing the chattering phenomenon, the sliding layer concept is one of the simplest and most widely applied. As shown in Figure 4, the sliding layer control strategy replaces the sign (σ) function with the following function [17]:

$$ ()

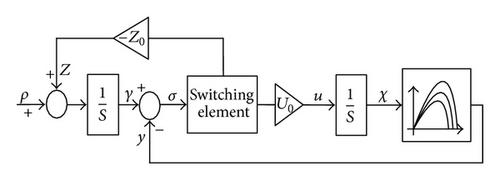
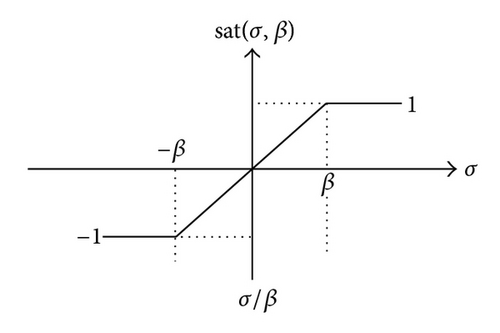
According to (8), the system space is divided into three regions, namely, σ > β, |σ| ≤ β, and σ < −β, where |σ| ≤ β represents the sliding layer. Furthermore, the robustness of the proposed SMESC controller is ensured by specifying Z₀ ≫ ρ, while the response time and stability are enhanced by determining the optimal value of the gain constant (U₀) using a particle swarm optimization (PSO) algorithm. The details of the PSO algorithm are described in the following section.

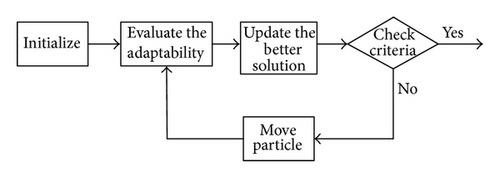
3. Particle Swarm Optimization (PSO) Algorithm

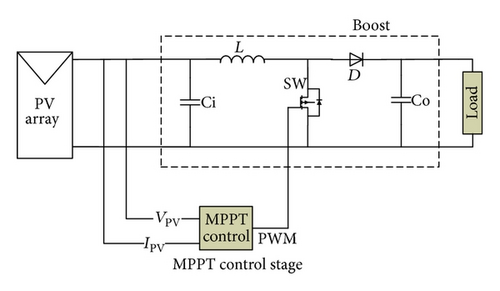
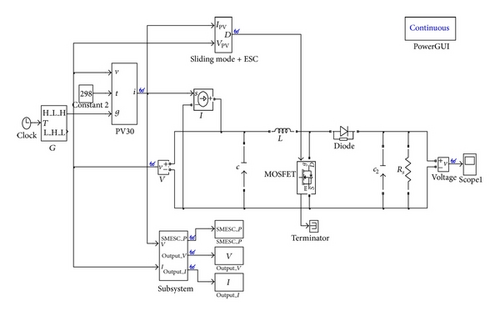
4. System Circuit Architecture

5. Simulation and Experimental Results

In this study, the performance of the proposed SMESC controller was evaluated both numerically and experimentally and was compared with that of two existing gradient detection-based MPPT algorithms, that is, P&O [20] and INC [21].

In both the simulations and the experimental investigation, the solar panel was a KYOCER KC30 panel with the specification shown in Table 1. As described in the previous section, the MPPT algorithm was implemented using a dSPACE R&D control board. The numerical and experimental investigations considered two general irradiance conditions, namely (1) uniform irradiance (1000 W/m²), and (2) nonuniform irradiance, that is, (i) a reduction from 1000 W/m² to 400 W/m² followed by a return to 1000 W/m² and (ii) an increase from 400 W/m² to 1000 W/m² followed by a return to 400 W/m².

5.1. Use of PSO Algorithm to Determine Optimal Value of Control Gain

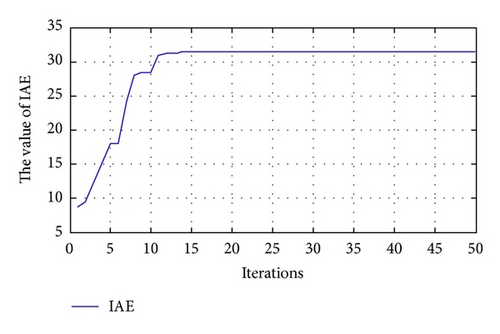
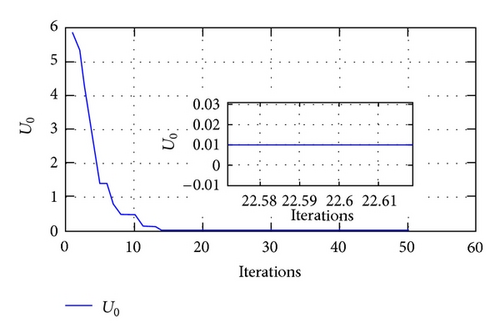
As shown in Table 1, the solar panel has a maximum power of 30 W (i.e., ρ = 30). As discussed in Section 2, Z₀ should be far greater than ρ in order to ensure the robustness and stability of the proposed SMESC scheme. Accordingly, in the present investigations, Z₀ was specified as 100. Meanwhile, the optimal value of the control gain U₀ was obtained using the PSO optimization scheme. Figure 7 shows the convergence behavior of the PSO algorithm, while Figure 8 shows the convergence of U₀. It is seen in Figure 7 that the PSO algorithm converges after 15 iterations. From Figure 8, the optimal value of the control gain is equal to U₀ = 0.01. (Note that a gain of U₀ = 0.01 was therefore applied in all of the remaining simulations and experiments.)

5.2. Simulation Results

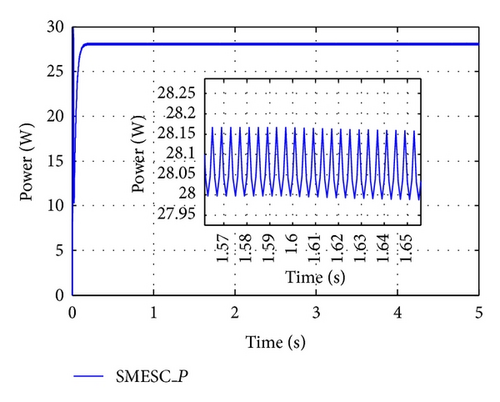
Figure 9 illustrates the simulation model adopted in the present study. Figure 10 presents the simulation results obtained for the output power using the proposed SMESC scheme given a uniform irradiance of 1000 W/m². It is seen that the SMESC scheme enables a rapid and precise tracking of the MPP. Furthermore, it is observed that the proposed scheme yields a stable steady-state response.

To evaluate the robustness and ability of the SMESC scheme to track the MPP given dramatic variations in the irradiance conditions, a simulation was performed in which the irradiance was suddenly reduced from 1000 W/m² to 400 W/m² after 1.5 s and then restored to 1000 W/m² after an interval of 2.5 s. The corresponding simulation results for the output power are shown in Figure 11. The results confirm that the SMESC controller rapidly tracks the MPP as the irradiance is first reduced and then increased. Figure 12 shows the simulated output power for the case where the irradiance is increased abruptly from 400 W/m² to 1000 W/m² after 1.5 s and then reduced to 400 W/m² after a further 2.5 s. The results again confirm the robustness and ability of the SMESC scheme to rapidly track the MPP given a dramatic variation in the irradiance intensity.

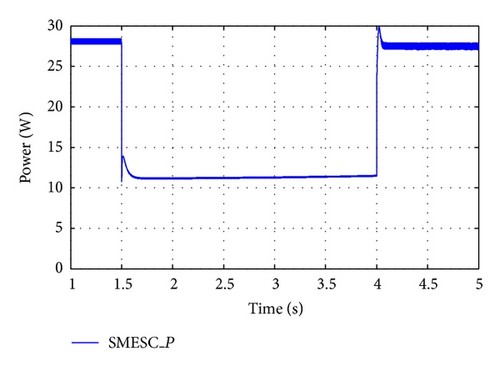
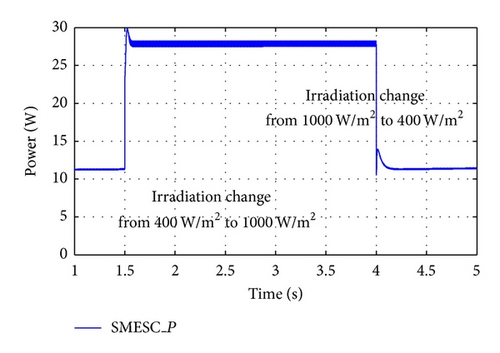
Figure 13 compares the MPPT performance of the P&O, INC, and SMESC schemes given a uniform irradiance of 1000 W/m². As shown, the P&O scheme results in violent fluctuations in the output power under steady-state conditions and therefore leads to a significant energy loss. It is seen that the INC scheme results in an improved steady-state performance. However, fluctuations in the output power are still observed. Furthermore, the tracking performance of INC is highly sensitive to the accuracy of the signal measurements and is therefore liable to significant error in real-world implementations. Notably, the P&O and INC methods both use a gradient detection-based approach to identify the system signals. The resulting ultra-high switching frequency not only leads to energy loss but also increases the risk of component damage. It is seen that the proposed SMESC scheme results in a far better steady-state performance than the P&O or INC scheme. In other words, the results confirm the effectiveness of the sliding layer control scheme in suppressing the chattering phenomenon and reducing power loss as a result.

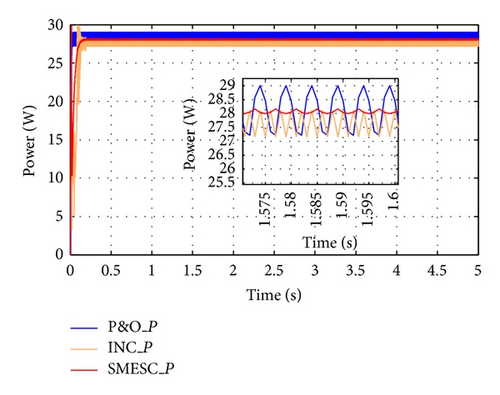
5.3. Experimental Results

Having demonstrated the basic validity of the proposed SMESC controller via MATLAB simulations, a series of experimental investigations was performed using the hardware architecture shown in Figure 14 to evaluate the real-world applicability of the proposed scheme.

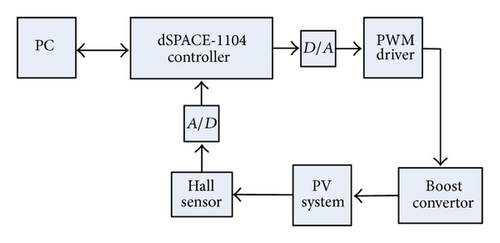
Figure 15 presents a block diagram showing the implementation of the SMESC scheme using the dSPACE control board. Note that “Filter_V” and “Filter_I” are wave filters, “Sliding mode” is the sliding controller, “SMESC” is the proposed Sliding Mode extremum seeking control scheme, and “PWM” is the PWM circuit.

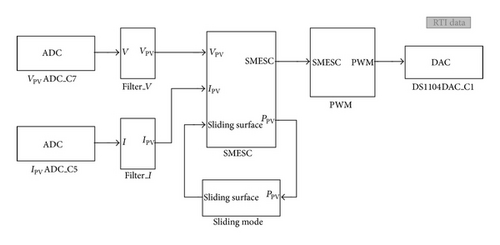
Figure 16 shows the experimental results obtained for the output power given a uniform irradiance of 1000 W/m². The results confirm the ability of the proposed control scheme to ensure the system stability and efficiency under steady-state conditions. In addition, it is observed that the SMESC controller responds rapidly to the step change in the irradiance, thereby further reducing energy losses during the MPPT procedure.

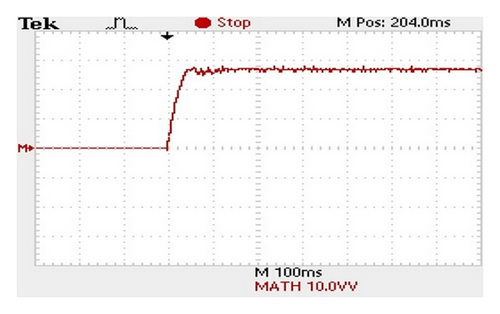
Figure 17 shows the experimental results for the output power waveform given a sudden reduction of the irradiance from 1000 W/m² to 400 W/m² followed by an abrupt return to an irradiance of 1000 W/m² after an interval of 2.5 s. It is seen that the SMESC controller accurately and rapidly tracks the MPP as the irradiance is first reduced and then increased. Figure 18 presents the experimental output power waveform for the case in which the irradiance is first increased from 400 W/m² to 1000 W/m² and then restored to 400 W/m². The results again confirm that the proposed scheme yields both a rapid transient response and a stable steady-state response.

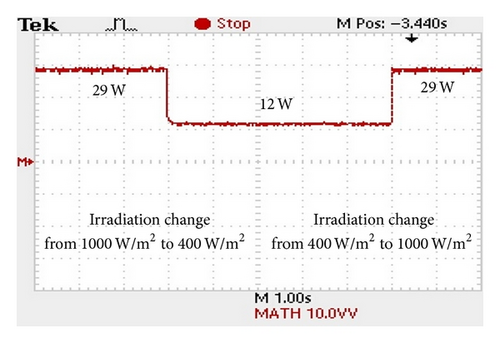
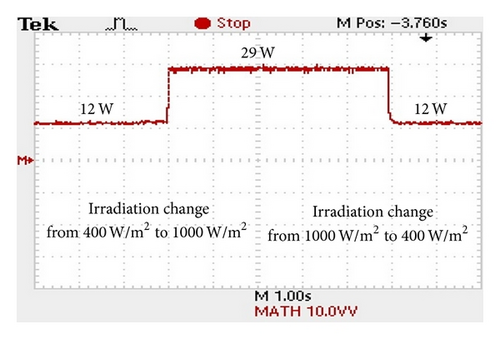
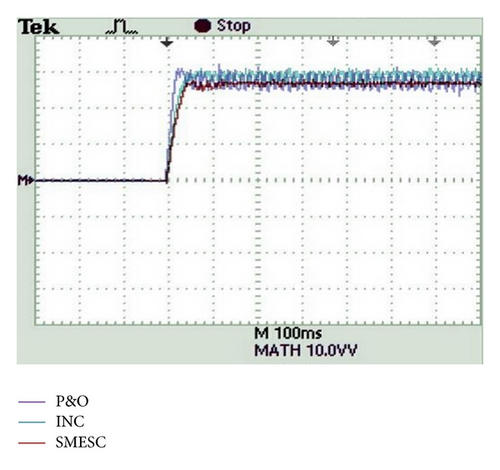
Figure 19 compares the experimental output power waveforms obtained using the P&O, INC, and SMESC control schemes, respectively, given a uniform irradiance of 1000 W/m². The results show that the P&O scheme leads to significant oscillations in the output power under steady-state conditions. Thus, while the P&O scheme has a simple architecture and is easily implemented, it has poor efficiency and results in significant power losses. It is seen that the INC scheme yields a lower steady-state oscillation of the output power waveform than the P&O method. However, the tracking accuracy and efficiency of INC are both highly sensitive to the accuracy of the sensors used to acquire the system signal. The results presented in Figure 19 confirm that the proposed SMESC scheme successfully resolves the chattering phenomenon associated with traditional gradient detection-based methods and yields an accurate and highly efficient MPP tracking performance.

6. Conclusions

This study has proposed a sliding mode extremum seeking control (SMESC) scheme for maximum power point (MPP) tracking in photovoltaic power generation systems. In the proposed approach, the chattering phenomenon associated with the ultrahigh switching frequency required in traditional gradient-detection methods is suppressed by means of a sliding layer concept. Moreover, the response time and stability of the proposed control scheme are enhanced by using a particle swarm optimization algorithm to determine the optimal value of the control gain. The validity of the proposed scheme has been investigated numerically and experimentally under both uniform irradiance conditions and rapidly varying irradiance conditions. The results have shown that the proposed scheme provides a rapid and highly accurate MPP tracking performance. In addition, it has been shown that the scheme minimizes oscillations in the output power under steady-state conditions and therefore results in a better efficiency than traditional MPPT algorithms such as P&O [20] and INC [21].