Alternating direction implicit (ADI) schemes are proposed for the solution of the two-dimensional coupled nonlinear Schrödinger equation. These schemes are of second- and fourth-order accuracy in space and second order in time. The resulting schemes in each ADI computation step correspond to a block tridiagonal system which can be solved by using one-dimensional block tridiagonal algorithm with a considerable saving in computational time. These schemes are very well suited for parallel implementation on a high performance system with many processors due to the nature of the computation that involves solving the same block tridiagonal systems with many right hand sides. Numerical experiments on one processor system are conducted to demonstrate the efficiency and accuracy of these schemes by comparing them with the analytic solutions. The results show that the proposed schemes give highly accurate results.

1. Introduction

In this paper, we consider the coupled nonlinear Schrödinger equation

()

with initial conditions

()

and Dirichlet boundary conditions

()

where Ω is a rectangular domain in ℝ². We assume that Ω = [a, b] × [c, d], ∂Ω is the boundary of Ω, (0, T] is the time interval, and f₁(x, y), f₂(x, y), g₁(x, y, t), and g₂(x, y, t) are given sufficiently smooth functions. The two functions ψ(x, y, t), ϕ(x, y, t) are representing the amplitudes of the two circularly polarized waves. The values of α vary over a wide range; that is, α ≥ 2/3 and α ≤ 7 correspond to kerr type electronic nonlinearity [1]. The physical significance of system (1) can be seen in the transverse effects in nonlinear optics. Since solitons interact like particles, the studies for the interactions of solitons have been of both experimental and theoretical interest. Many numerical methods have been developed for solving the coupled nonlinear Schrödinger [2–6]. Many published works for solving the two-dimensional nonlinear Schrödinger equation are given in [7–11]. In this work, we are going to derive an ADI method for solving the two-dimensional coupled nonlinear Schrödinger equation.

In this paper, we derive two ADI schemes for solving the two-dimensional coupled nonlinear Schrödinger system, one is of second order in space and time directions, and the other one is of fourth order in space and second order in time. Both methods are producing a block nonlinear tridiagonal system; a fixed point method has been developed to solve this system. The proposed schemes are unconditionally stable using Fourier stability analysis.

The ADI method [8–15], which replaces the solution of multidimensional problems by sequences of one-dimensional cases, only needs to solve tridiagonal linear system or block tridiagonal systems, and the resulting schemes are unconditionally stable and received much attention in recent years.

Following Biswas [16], we derive the soliton solution of the system (1) which can be written as

()

where

()

and α, β₁, β₂, k₁, and k₂ are arbitrary constants (see the appendix). The system has the conserved quantities [15]

()

To avoid the complex computation, we assume

()

The system (1) can be written as

()

where

()

System (10) can be written in matrix vector form as

()

where

()

The paper is organized as follows. In Section 2 we give two ADI schemes for solving the two-dimensional coupled nonlinear Schrödinger equation, and in Section 3, we present the von Neumann stability analysis for the proposed schemes. Numerical experiments for several problems are presented in Section 4. A parallel algorithm for the proposed ADI schemes is given in Section 5. Conclusions are given in Section 6.

2. Numerical Method

To derive the numerical schemes for solving system (1), we consider the domain of interest Ω = [a, b] × [a, b], such that (x, y) ∈ Ω. The domain is divided by a uniform mesh in each direction such that

()

where h and k are the space and time step sizes, respectively. We denote

and

to be the exact and the numerical solutions at the point (x_l, y_m, t_n), respectively.

2.1. Second-Order ADI Method

To derive the first scheme, we approximate the space derivative using the central difference formulae

()

We apply (15) to system (12); this will lead us to the following first order differential system in time

()

Equation (16) is of second order in space.

By applying the Crank-Nicolson method for the temporal discretization, we get the following difference scheme with accuracy O(k² + h²):

()

where

()

This scheme can be written as

()

which can be approximated by using the factored form

()

By Taylor’s expansion, the last term in (20) can be written as

()

which is of the same order of accuracy of the truncation error, and we ignore it to obtain

()

By introducing a new intermediate vector

, we propose a D’Yakonov [12, 17] ADI-like scheme for the coupled system

()

which is a nonlinear scheme. An iterative algorithm of fixed point nature can be used to solve the system of the nonlinear equations (23)-(24). The fixed point that we propose can be given by

()

where the superscript s denotes the sth iterate for solving the nonlinear system of equations for each time step. The block tridiagonal matrix equations of (25) can be solved by Crout’s method. The initial iterate

is chosen as

()

The iteration continues until the condition

()

is satisfied.

The boundary value of the intermediate variable

can be extracted from (24) and is given by the following formulas:

()

2.2. Fourth-Order ADI Method

Now, we want to derive a highly accurate fourth order ADI scheme; to do this, we approximate the space derivatives by the following formulas

()

By using these approximations together with Crank-Nicolson for the time direction, we get the numerical scheme

()

which can be written as

()

and this can be written in the factored form as

()

The difference between (31) and (32) is

()

which is of the same order of accuracy of the truncation error, we ignore it, and then we operate on both sides of (32) by

()

The fourth-order D’Yakonov ADI-like scheme in this case can be displayed as

()

Now the systems in (35) and (36) are nonlinear. By the similar approach used in the previous scheme, we can derive a fixed point iterative formulas.

The boundary value of the intermediate variable

in (35) can be given by the following formulas:

()

We can easily write a generalized version of D’Yakonov ADI like method for solving the two-dimensional coupled nonlinear Schrödinger system (1) as

()

for arbitrary value of σ, and for σ = 0, σ = 1/12 we recover the second- and fourth-order schemes, respectively.

3. Stability Analysis

To study the stability of the proposed scheme, we consider the von Neumann stability analysis which can be only applied for the linear finite difference scheme, so we consider the linear version of the generalized scheme

()

where ω is constant and σ = 0, 1/12.

Suppose that the numerical solution can be expressed by Fourier series, whose typical term is

()

where

is the amplification matrix at time level n, and β₁, β₂ are the wave numbers in x and y directions. Substituting (40) into (39) will lead to the matrix equation

()

where

()

The eigenvalues of the matrix G are given by

()

It can be easily shown that the modulus of the maximum eigenvalue of the amplification matrix G is less than one; hence, the scheme is unconditionally stable according to the von Neumann stability analysis.

4. Numerical Results

In this section, the efficiency and accuracy of the proposed schemes will be tested by comparing with the exact solutions. We will measure the accuracy of the proposed schemes using the L_∞ norm. We compute the conserved quantity by using the trapezoidal rule.

4.1. Example 1

In this example, we choose the initial conditions from the exact solutions

()

where

()

at t = 0. The following parameters are used

()

The boundary conditions are extracted from the exact solution (44).

Tables 1, 2, and 3 show the errors (ER) and the conserved quantities (I) for σ = 0, 1/6 and σ = 1/12, respectively. We have noticed that the scheme with σ = 1/12 produced highly accurate results, and this is due to the fourth order accuracy in space and second-order accuracy in time. The other two methods using σ = 0 and σ = 1/6 are of second-order accuracy in space and time. Figure 1 shows a single soliton at t = 0. Figure 2 shows the numerical solution at t = 1.

Table 1. Single soliton with σ = 0.

Iter	T	ER	I
0	0	0	24.99989
2	0.2	0.00435	25.00086
2	0.4	0.00886	25.00291
2	0.6	0.01365	25.00586
2	0.8	0.01893	25.00973
2	1.0	0.02439	25.01458

Table 2. Single soliton with σ = 1/6.

Iter	T	ER	I
0	0	0	24.99989
2	0.2	0.00436	24.99882
2	0.4	0.00859	24.99664
2	0.6	0.01277	24.99351
2	0.8	0.01750	24.98938
2	1.0	0.02206	24.98417

Table 3. Single soliton with σ = 1/12.

Iter	T	ER	I
0	0	0	24.99989
2	0.2	0.00011	24.99989
2	0.4	0.00018	24.99987
2	0.6	0.00025	24.99981
2	0.8	0.00030	24.99971
2	1.0	0.00036	24.99952

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Single soliton β₁ = κ₁ = 0.5, β₂ = κ₂ = 1, α = 1, t = 0.

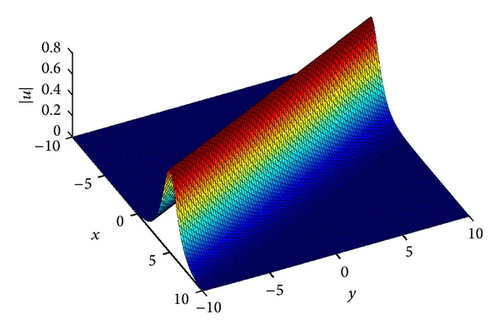
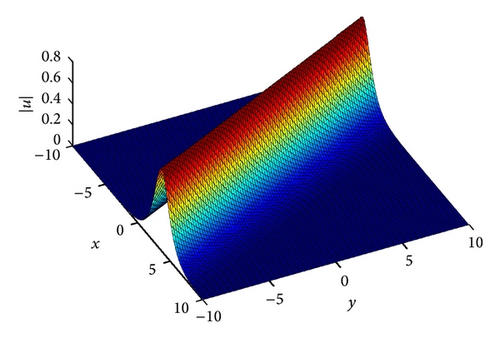
4.2. Example 2

In this example we will choose the initial condition [1]

()

where

()

which represent two solitons of different amplitudes. The parameters α₁, β₁, κ₁, and l₁ are complex parameters. In this test, we choose the parameters

()

In Figures 3 and 4, we display the numerical solution of |ψ|² at t = 0 and t = 1, while in Figures 5 and 6 we display the numerical solution of |ϕ|² at t = 0 and t = 1.

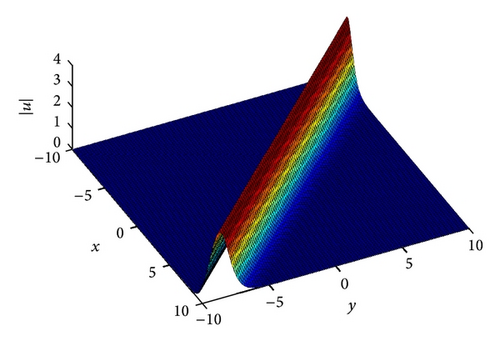
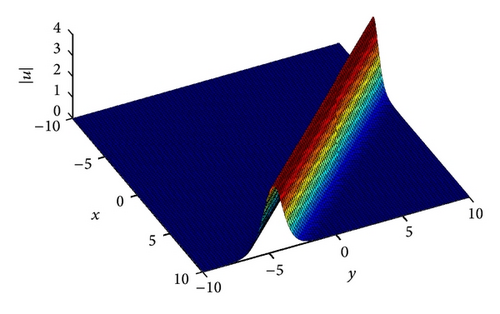
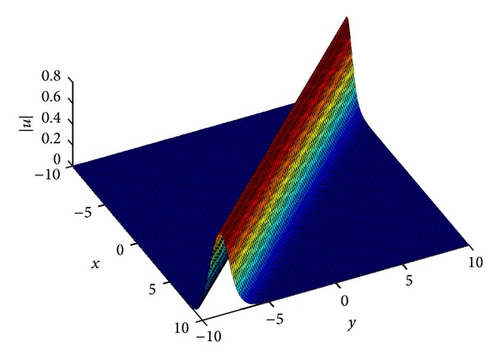
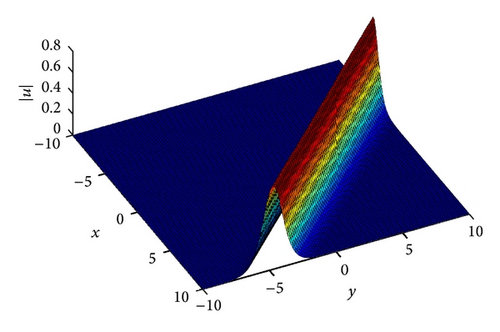
4.3. Example 3

To study the interaction of two solitons, many numerical tests have been conducted with different initial conditions, and, among these tests, we select the initial conditions of the form

()

which represent two solitons moving in the opposite direction and centered at d and −d, respectively. In this test we choose the parameters

()

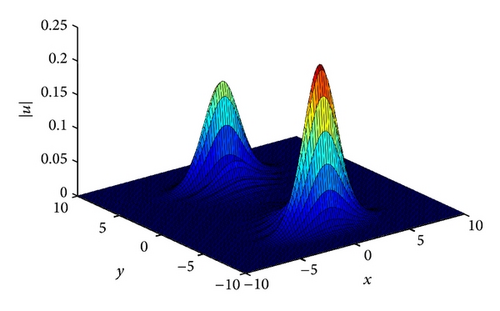
The interaction scenario is given in Figures 7 and 8. In Figure 7 we show the two solitons with two different amplitudes at t = 0. In Figure 8 we display the interaction where the two solitons interact at t = 0.5, and, in Figure 9, we display the two solitons after the interaction at t = 1.5. In Table 4, we display the conserved quantities, and we see that the numerical method we proposed conserves the conserved quantities almost exactly. It is easy to see that the interaction regiem is an inelastic one. See [18].

Table 4. The conserved quantities during the interaction scenario.

T	I₁	I₂
0.0	1.57080	1.00531
0.5	1.57086	1.00533
1.0	1.57065	1.00522
1.5	1.57060	1.00520

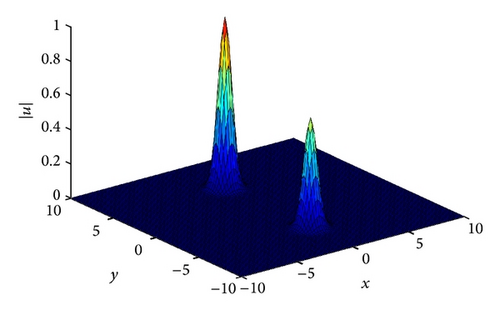
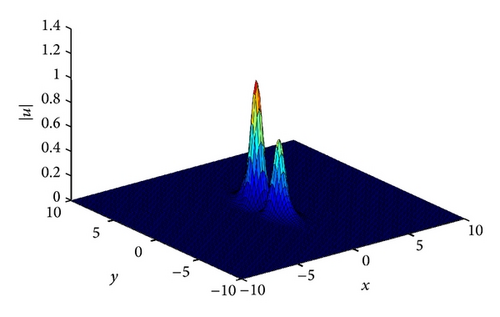
4.4. Example 4

The system under consideration generates a progressive plane wave solutions [7]:

()

where

()

Our numerical experiments are conducted in the domain [0,2π] × [0,2π] with

()

Initial and boundary conditions are extracted from the exact solution. In this example we choose σ = 1/12, the fourth order ADI method. The numerical results are presented in Table 5. Figure 10 displays the solution at t = 0, and Figure 11 displays, the solution at t = 1.

Table 5. Periodic solution k₁ = k₂ = α = 1.

Iter	T	ER	I
0	0.0	0.000000	39.478420
2	0.2	0.000003	39.478420
2	0.4	0.000005	39.478420
2	0.6	0.000007	39.478420
2	0.8	0.000009	39.478420
2	1.0	0.000008	39.478420

Table 4 displays the accuracy of the scheme and preserves the conserved quantities.

5. Parallel Algorithm for the Proposed ADI Schemes

It is to be noted that the implementation of the ADI schemes requires solving the same block-tridiagonal matrix with different right-hand sides. This can be done efficiently by using the fast parallel algorithm given in [19]. This algorithm [19] is a generalization of the parallel dichotomy algorithm for solving tridiagonal liner system of equations [20].

It has been shown that this dichotomy yields almost a linear speedup on a high performance system with many processors [19]. We expect the same speedup for our proposed methods. The parallel implementation of the proposed ADI method will be reported in our future work.

6. Concluding Remarks

In this present work, a generalized alternating direction implicit methods for solving two-dimensional coupled nonlinear Schrödinger equation have been established, the methods are unconditionally stable. The methods produced schemes of second and fourth order accuracy in space and second order in time according to the selected value of σ. The numerical results have shown that the proposed schemes successfully combine accuracy and efficiency for the two-dimensional coupled nonlinear Schrödinger system. The implementation of the ADI schemes requires solving the same block-tridiagonal matrix with different right-hand sides. This can be done by using the fast parallel algorithm given in [19]. This algorithm yields almost a linear speedup on a high performance system with many processors [19]. We expect the same speedup for our proposed methods. The proposed schemes can be easily extended to solve higher dimensional coupled nonlinear Schrödinger system.

Acknowledgments

This work was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under Grant no. (130-074-D1433). The authors, therefore, acknowledge with thanks the DSR technical and financial support.

Appendix

The exact solution of the nonlinear system can be derived as follows: we assume [19]

where

Now from (A.1), we deduce

and similar expressions can be obtained for the function ϕ. By substituting these expressions into the given system, and equating the real and imaginary parts, this will produce the following relations:

By equating the coefficient of sech³(ξ) in (A.5), we obtain

and by equating the coefficients of sech(ξ), we will get the relation

From the second equation of the proposed system (ϕ), we will get the relation

and from (A.6) and (A.8), we deduce that A = B, and then we get the relation

with α, β, κ, and l as arbitrary complex parameters.

References

1 Zhang H.-Q., Meng X.-H., Xu T., Li L.-L., and Tian B., Interactions of bright solitons for the (2 + 1)-dimensional coupled nonlinear Schrödinger equations from optical fibres with symbolic computation, Physica Scripta. (2007) 75, no. 4, 537–542, https://doi.org/10.1088/0031-8949/75/4/028, MR2299235.
10.1088/0031-8949/75/4/028
CAS Web of Science® Google Scholar
2 Ismail M. S. and Taha T. R., Numerical simulation of coupled nonlinear Schrödinger equation, Mathematics and Computers in Simulation B. (2001) 56, no. 6, 547–562, https://doi.org/10.1016/S0378-4754(01)00324-X, MR1842579, ZBL0972.78022.
10.1016/S0378-4754(01)00324-X
Web of Science® Google Scholar
3 Ismail M. S., A fourth-order explicit schemes for the coupled nonlinear Schrödinger equation, Applied Mathematics and Computation. (2008) 196, no. 1, 273–284, https://doi.org/10.1016/j.amc.2007.05.059, MR2382611, ZBL1133.65063.
10.1016/j.amc.2007.05.059
Web of Science® Google Scholar
4 Ismail M. S., Numerical solution of coupled nonlinear Schrödinger equation by Galerkin method, Mathematics and Computers in Simulation. (2008) 78, no. 4, 532–547, https://doi.org/10.1016/j.matcom.2007.07.003, MR2424561, ZBL1145.65075.
10.1016/j.matcom.2007.07.003
Web of Science® Google Scholar
5 Ismail M. S. and Alamri S. Z., Highly accurate finite difference method for coupled nonlinear Schrödinger equation, International Journal of Computer Mathematics. (2004) 81, no. 3, 333–351, https://doi.org/10.1080/00207160410001661339, MR2174995, ZBL1058.65090.
10.1080/00207160410001661339
Web of Science® Google Scholar
6 Taha T. R. and Xu X., Parallel split-step fourier methods for the coupled nonlinear Schrödinger type equations, The Journal of Supercomputing. (2005) 32, no. 1, 5–23, 2-s2.0-17444407059, https://doi.org/10.1007/s11227-005-0183-5.
10.1007/s11227-005-0183-5
Web of Science® Google Scholar
7 Gao Z. and Xie S., Fourth-order alternating direction implicit compact finite difference schemes for two-dimensional Schrödinger equations, Applied Numerical Mathematics. (2011) 61, no. 4, 593–614, https://doi.org/10.1016/j.apnum.2010.12.004, MR2754579, ZBL1221.65220.
10.1016/j.apnum.2010.12.004
Web of Science® Google Scholar
8 Kong L., Duan Y., Wang L., Yin X., and Ma Y., Spectral-like resolution compact ADI finite difference method for the multi-dimensional Schrödinger equations, Mathematical and Computer Modelling. (2012) 55, no. 5-6, 1798–1812, https://doi.org/10.1016/j.mcm.2011.11.036, MR2899125, ZBL1255.81014.
10.1016/j.mcm.2011.11.036
Web of Science® Google Scholar
9 Tian Z. F. and Yu P. X., High-order compact ADI (HOC-ADI) method for solving unsteady 2D Schrödinger equation, Computer Physics Communications. (2010) 181, no. 5, 861–868, https://doi.org/10.1016/j.cpc.2009.12.022, MR2599941, ZBL1205.65240.
10.1016/j.cpc.2009.12.022
CAS Web of Science® Google Scholar
10 Wang T., Guo B., and Xu Q., Fourth order compact and energy conservative difference schemes for the nonlinear Schrödinger equation in two dimensions, Journal of Computational Physics. (2013) 243, 382–399.
10.1016/j.jcp.2013.03.007
Web of Science® Google Scholar
11 Xu Y. and Zhang L., Alternating direction implicit method for solving two-dimensional cubic nonlinear Schrödinger equation, Computer Physics Communications. (2012) 183, no. 5, 1082–1093, https://doi.org/10.1016/j.cpc.2012.01.006, MR2888993.
10.1016/j.cpc.2012.01.006
CAS Web of Science® Google Scholar
12 Karaa S. and Zhang J., High order ADI method for solving unsteady convection-diffusion problems, Journal of Computational Physics. (2004) 198, no. 1, 1–9, https://doi.org/10.1016/j.jcp.2004.01.002, MR2071388, ZBL1053.65067.
10.1016/j.jcp.2004.01.002
Web of Science® Google Scholar
13 Sapagovas M. and Jakubeliene K., Alternating direction method for two-dimensional parabolic equation with nonlocal integral condition, Nonlinear Analysis. (2012) 17, no. 1, 91–98, MR2897912.
10.15388/NA.17.1.14080
Google Scholar
14 Subasi M., On the finite difference schemes for the numerical solution of two dimensional Schrödinger equation, Numerical Methods for Partial Differential Equations. (2002) 18, 124–134.
10.1002/num.10029
Web of Science® Google Scholar
15 You D., A high-order Padé ADI method for unsteady convection-diffusion equations, Journal of Computational Physics. (2006) 214, no. 1, 1–11, https://doi.org/10.1016/j.jcp.2005.10.001, MR2208668, ZBL1089.65092.
10.1016/j.jcp.2005.10.001
Web of Science® Google Scholar
16 Biswas A., 1-soliton solution of 1 + 2 dimensional nonlinear Schrödinger equations in power law media, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, 1830–1833.
10.1016/j.cnsns.2008.08.003
Web of Science® Google Scholar
17 Mitchell A. R. and Griffiths D. F., The Finite Difference Method in Partial Differential Equations, 1980, John Wiley & Sons, Chichester, UK, MR562915.
Google Scholar
18 Besse C., Mauser N. J., and Stimming H. P., Numerical studies for nonlinear Schrodinger equations: the Schrodinger-Poisson-Xα model and Davey Stewartson systems, In press.
Google Scholar
19 Terekhov A. V., A fast parallel algorithm for solving block-tridiagonal systems of liner equations including the domain decomposition method, Parallel Computing. (2013) 39, 245–258.
10.1016/j.parco.2013.03.003
Web of Science® Google Scholar
20 Terekhov A. V., Parallel dichotomy algorithm for solving tridiagonal system of linear equations with multiple right-hand sides, Parallel Computing. (2010) 36, no. 8, 423–438, https://doi.org/10.1016/j.parco.2010.02.005, MR2680699, ZBL1205.68502.
10.1016/j.parco.2010.02.005
Web of Science® Google Scholar

Citing Literature

All articles

Parallel Methods and Higher Dimensional NLS Equations

Abstract

1. Introduction