This paper further investigates the problem of finite-time state feedback stabilization for a class of stochastic nonholonomic systems in chained form. Compared with the existing literature, the stochastic nonholonomic systems under investigation have more uncertainties, such as the x₀-subsystem contains stochastic disturbance. This renders the existing finite-time control methods highly difficult to the control problem of the systems or even inapplicable. In this paper, by extending adding a power integrator design method to a stochastic system and by skillfully constructing C² Lyapunov function, a novel switching control strategy is proposed, which renders that the states of closed-loop system are almost surely regulated to zero in a finite time. A simulation example is provided to demonstrate the effectiveness of the theoretical results.

1. Introduction

The nonholonomic systems, which can be used to model many frequently met mechanical systems, such as wheeled mobile robot, knife edge and rolling disk, have been an active research field over the past decades. From Brockett’s necessary condition [1], it is well known that the nonholonomic systems cannot be stabilized to the origin by any static continuous state feedback, so the classical smooth control theory cannot be applied directly. In order to overcome this obstruction, several novel approaches have been developed for the problem, such as discontinuous time-invariant stabilization [2, 3], smooth time-varying stabilization [4–6], and hybrid stabilization [7]. Using these valid approaches, many fruitful results have been developed [8–15]. Particularly, the stochastic nonholonomic systems, which can be viewed as the extension of the classical nonholonomic systems, have been recently achieved investigations [16–18]. However, it should be noted that those aforementioned papers consider the feedback stabilizer that makes the trajectories of the systems converge to the equilibrium as the time goes to infinity.

Compared to asymptotic stabilization, the closed-loop system with finite-time convergence usually demonstrates faster convergence rates, higher accuracies, better disturbance rejection properties, and robustness against uncertainties [19]. Hence, it is more meaningful to investigate the finite-time stabilization problem than the classical asymptotical stability. For the deterministic case, in [20], a novel switching finite-time control strategy was proposed to nonholonomic systems in a chained form with uncertain parameters and perturbed terms by the use of time rescaling and Lyapunov based method. Later this result was essentially extended under weaker constraints on drift terms in [21]. As a natural extension, the finite-time stabilization for stochastic nonholonomic systems is an interesting and challenging subject of intensive study. However, it cannot be solved by simply extending the methods for deterministic systems because of the presence of stochastic disturbance. As pointed out by Yin et al. [22], “the existence of a unique solution and the non-satisfaction of local Lipschitz condition are two prerequisites of discussing the finite-time stability for a stochastic nonlinear system. That is, as a common assumption condition to guarantee the existence of a unique solution for stochastic nonlinear system, local Lipschitz condition cannot be applied to study stochastic finite-time stability.” Therefore, the finite-time controller design for stochastic nonholonomic systems should solve the following questions: under what conditions, the stochastic nonholonomic systems exist possibly finite-time stabilizer? Under these conditions, how can one design a finite-time state feedback stabilizing controller?

To the best of the authors’ knowledge, only the authors in [23] considered the aforementioned problems when the x₀-subsystem is ordinary differential equation. This paper continues the investigation in [23] and addresses the finite-time stabilizing control design for stochastic nonholonomic systems with more uncertainties than those in [16–18, 23], which cannot be handled by general existing methods. A constructive method in designing finite-time stabilizing controller for such uncertain system is proposed. The contribution of this paper is highlighted as follows. First, inspired by the deterministic works in [24, 25], we generalize adding a power integrator design method [26] to a stochastic system, and a novel C² Lyapunov function is constructed to deal with stochastic disturbances. Second, based on a new switching method, a systematic control design procedure is proposed to solve the finite-time stabilization problem for all plants in the considered class.

The remainder of this paper is organized as follows. Section 2 presents some necessary notations, definitions, and preliminary results. Section 3 describes the systems to be studied and formulates the control problem. Section 4 presents the design scheme to the controller and the main result. Section 5 gives a simulation example to illustrate the theoretical finding of this paper. Finally, concluding remarks are proposed in Section 6.

2. Notations and Preliminary Results

The following notations, definitions, and lemmas are to be used throughout the paper. R⁺ denotes the set of all nonnegative real numbers, and Rⁿ denotes the real n-dimensional space. (a, b) _odd denotes the set {x∣x = p/q and x ∈ (a, b), where p and q are odd integers}. (a, b) _even denotes the set {x∣x = p/q and x ∈ (a, b), where p is an even integer and q is an odd integer}. For a given vector or matrix X, X^T denotes its transpose, Tr {X} denotes its trace when X is square, and |X| is the Euclidean norm of a vector X. Cⁱ denotes the set of all functions with continuous ith partial derivatives. K denotes the set of all functions: R⁺ → R⁺, which are continuous, strictly increasing, and vanishing at zero; K_∞ denotes the set of all functions which are of class K and unbounded. The arguments of the functions (or the functionals) will be omitted or simplified, whenever no confusion can arise from the context. For instance, we sometimes denote a function f(x(t)) by simply f(x) or f.

We begin with some basic concepts and terminologies related to the notion of stochastic finite-time stability. The reader is referred to [22, 27, 28] as well as the references therein for additional details.

Consider the stochastic nonlinear system

()

where x ∈ Rⁿ is the system state with the initial condition x(0) = x₀; ω is an m-dimensional independent standard Wiener process defined on a complete probability space (Ω, ℱ, {ℱ_t} _t≥0, P) with Ω being a sample space, ℱ being a σ-field, {ℱ_t} _t≥0 being a filtration, and P being a probability measure. The functions: f : R⁺ × Rⁿ → Rⁿ and g : R⁺ × Rⁿ → R^n×m are piecewise continuous and continuous with respect to the first and second arguments, respectively, and satisfy f(t, 0) ≡ 0 and g(t, 0) ≡ 0. Moreover, system (1) is assumed to have a pathwise unique strong solution, denoted by x(t, x₀).

Definition 1. For system (1), define T₀(x₀, w) = inf {T ≥ 0 : x(t, x₀) = 0, for all t ≥ T}, which is called the stochastic settling time function. Especially, T₀(x₀, w): = +∞ if x(t, x₀) ≠ 0, for all t ≥ 0.

Definition 2. The equilibrium x ≡ 0 of the system (1) is said to be a stochastic finite-time stable equilibrium if

(i)
it is stable in probability: for every pair of ε ∈ (0,1) and r > 0, there exists δ > 0 such that P{|x(t, x₀)| < r, for all t ≥ 0} ≥ 1 − ε, whenever | x | < δ;
(ii)
its stochastic settling-time function T₀(x₀, w) exists finitely with probability and E[T₀(x₀, w)] < ∞.

Next, we give two lemmas where the first one provides sufficient conditions to ensure the existence of pathwise unique strong solution to system (1), and the other one has been used to determine the finite-time stability of stochastic nonlinear systems.

Lemma 3 (see [23], [29].)Assume that f(t, x) and g(t, x) are continuous in x. Further, for any 0 < δ < 1, each N = 1,2, …, and each 0 ≤ T < ∞, if the following conditions hold:

()

as 0 < δ ≤ |x_i| ≤ N, i = 1,2, t ∈ [0, T], where c(t) and

are nonnegative functions such that

and

. Then for any given x₀ ∈ Rⁿ, system (1) has a pathwise unique strong solution.

Lemma 4 (see [30].)Consider the stochastic nonlinear system described in (1). Suppose that there exist a C² function V(x), class K_∞ functions μ₁ and μ₂, real numbers c > 0 and 0 < α < 1, such that

()

Then it is globally finite-time stable in probability, and the stochastic settling time function T₀(x₀, w) satisfies

()

Then we list two lemmas that serve as the basis of the key tools for the adding a power integrator technique.

Lemma 5 (see [31].)For x ∈ R, y ∈ R, and p ≥ 1 being a constant, the following inequalities hold:

()

If p ≥ 1 is odd, then

()

Lemma 6 (see [32].)Let x, y be real variables; then for any positive real numbers a, m, and n, one has

()

where b > 0 is any real number.

3. Problem Formulation

Motivated by the statement in [18, 23] that many nonholonomic mechanical systems, such as wheeled mobile robot, subject to stochastic disturbances, can be transformed to a kind of stochastic nonholonomic systems in the so-called chained form, this paper considers the following class of stochastic nonholonomic systems in chained form:

()

where x₀ ∈ R and x = (x₁, …, x_n) ^T ∈ Rⁿ are system states and u₀ ∈ R and u₁ ∈ R are control inputs, respectively; d_i : R⁺ → R, i = 0, …, n are uncertain and continuous, called the control coefficients. The nonlinear functions f₀ : R⁺ × R → R and g₀ : R⁺ × R → R^m, f_i : R⁺ × Rⁱ⁺¹ → R and g_i : R⁺ × Rⁱ⁺¹ → R^m, i = 1, …, n are assumed to be C¹ with their arguments with f₀(t, 0) = 0, g₀(t, 0) = 0, f_i(t, x₀, 0) = 0 and g_i(t, x₀, 0) = 0. and ω is an m-dimensional independent standard Wiener process defined on a complete probability space (Ω, F, P) with Ω being a sample space, F being a filtration, and P being a probability measure.

Remark 7. Obviously, the stochastic nonholonomic system (8) contains more uncertainties in drift and diffusion terms than those in the closely related papers [16–18, 23]. This, especially the existence of stochastic disturbance in the x₀-subsystem, renders the procedure of control design in [23] inapplicable to the finite-time control problem of the system. Up to now, how to design a stabilizing controller to achieve the finite-time stabilization of the system (8) is unsolved. It is precisely our intention of this paper.

The following assumptions regarding system (8) are imposed throughout the paper.

Assumption 8. For i = 0, …, n, there are known positive constants c_i1 and c_i2 such that

()

Assumption 9. For f₀ and g₀, there are constants a > 0 and r ∈ (0,1) _odd such that

()

Assumption 10. For i = 1, …, n, there is a constant b > 0 such that for any τ ∈ (−2/(4n + 1), 0),

()

where m_i = 1 + (i − 1)τ.

For simplicity, in this paper we assume that τ = −p/q with p being any even integer and q being any odd integer, under which and the definition of m_i in Assumption 10, we know that m_i is an odd number.

Remark 11. Noting that f₀(t, 0) = 0, g₀(t, 0) = 0, f_i(t, x₀, 0) = 0 and g_i(t, x₀, 0) = 0 are assumed, Assumptions 9 and 10 imply that

()

It is noteworthy that Assumption 10 is a generalization of the homogeneous growth condition introduced in [33] where

and τ ≥ 0. Assumptions 9 and 10 are necessary, which play an essential role in ensuring the existence of finite-time stabilizer for stochastic nonholonomic system (8).

4. Finite-Time Control Design

In this section, we give a constructive procedure for the finite-time stabilizer of system (8). The design of finite-time state feedback controller is divided into two steps.

Step A. We first stabilize the x-subsystem in a finite time almost surely.

For the x₀-subsystem, we choose the control u₀ as

()

where

is a positive constant. In this case, the x₀-subsystem becomes

()

With the help of Assumptions 8 and 9 and Lemma 3, it easy to obtain that system (14) has a unique solution on [0, T], for any given finite time T > 0. Hence, x₀ is well defined on [0, T]. Next, we stabilize the x-subsystem

()

within a finite time. The control law u₁ can be recursively constructed by applying the method of adding a power integrator.

Step 1. Let

, where σ ∈ (2, ∞) _odd is a constant. Choosing the Lyapunov function

, where l is a constant satisfying 4l ∈ (0, ∞) _even and (4l − 2)σ ≥ 1. With the help of Remark 11 and Lemma 4, it can be verified that

()

Obviously, the first virtual controller

()

with design constant M > 0, results in

()

Inductive Step. Suppose at step k − 1, there are a C², proper and positive definite Lyapunov function V_k−1, and a set of virtual controllers

defined by

()

with constants β₁ > 0, …, β_k−1 > 0, such that

()

To complete the induction, at the kth step, we choose the following Lyapunov function:

()

where

()

Noting that

()

with the help of the fact σ/m_i > 2, the function V_k can be shown to be C², proper and positive definite using a similar method as in [34]. Moreover, we can obtain

()

where i, j = 1, …, k − 1, i ≠ j.

Using (20)–(22) and (24), it follows that

()

Based on Lemmas 5 and 6, the following proposition is given to estimate the last seven terms on the right-hand side of (25).

Proposition 12. There exists a positive constant l_k such that

()

Proof. The similar proof can be found in [23] and thus it is omitted here.

Substituting (26) into (25), we obtain

()

Clearly, the C⁰ virtual controller

()

with β_k > 0 being constant, results in

()

This completes the proof of the inductive step.

Using the previous inductive argument, one concludes that at the nth step, there exists a non-Lipschitz continuous state feedback control law of the form

()

with β_n > 0 being constant and a C² positive definite and proper Lyapunov function V_n of the form (21)-(22), such that

()

So the following result is obtained.

Lemma 13. If Assumptions 8 and 10 hold for the stochastic nonlinear system (15), then the solution of the closed-loop system consisting of (15) and (30) is finite-time stable in probability.

Proof. From (23) and (30), it is not hard to verify that all conditions in Lemma 3 are satisfied, which means that the closed-loop system admits a unique solution. Next we prove that the closed-loop system is globally finite-time stable in probability.

First of all, by using Lemma 5, it is easy to see that

()

So we have the following estimate

()

Let α = 4lσ/(4lσ − τ). With (33) and (31) in mind, by Lemma 5, it is not difficult to obtain that

()

Therefore, by Lemma 4, the uncertain system (15) with the controller (30) is globally finite-time stable in probability and its stochastic settling time T₁(x(0), w) satisfies

()

Step B. Then we design a state feedback controller such that the x₀-subsystem is finite-time stable in probability.

From Step A, we know that x(t) ≡ 0 when t ≥ T₁(x(0), w). Therefore, we just need to stabilize the x₀-subsystem in a finite time almost surely. When t ≥ T₁(x(0), w), for the x₀-subsystem, we can take the following control law:

()

where k₀ is a positive constant.

Taking the Lyapunov function

, a simple computation gives

()

Thus by Lemma 4, x₀ stochastically tends to 0 within a settling time denoted by T₂(x₀(0), w) and

()

Up to now, we have finished the finite-time stabilizing controller design of the system (8). Consequently, the following theorem can be obtained to summarize the main result of the paper.

Theorem 14. Under Assumptions 8–10, if the proposed control design procedure together with the previous switching control strategy is applied to system (8), then, for any initial conditions in the state space (x₀, x) ∈ Rⁿ⁺¹, the closed-loop system is globally finite time regulated at origin in probability.

Remark 15. The settling time of the closed-loop system depends on design parameters k₀, M and initial conditions, that is, when the initial conditions are known, the settling-time can be arbitrarily adjusted by the choice of appropriate design parameters k₀ and M.

5. Simulation Example

To verify our proposed controller, we consider the following low-dimensional system:

()

We choose τ = −2/11, which together with m₁ = 1 implies that m₂ = 9/11. By Lemma 5, it is verified that Assumptions 9-10 are satisfied with a = b = 1/2. Assumption 8 holds with 1 ≤ 1.5 + 0.5cos t ≤ 2; hence the controller proposed in this paper is applicable.

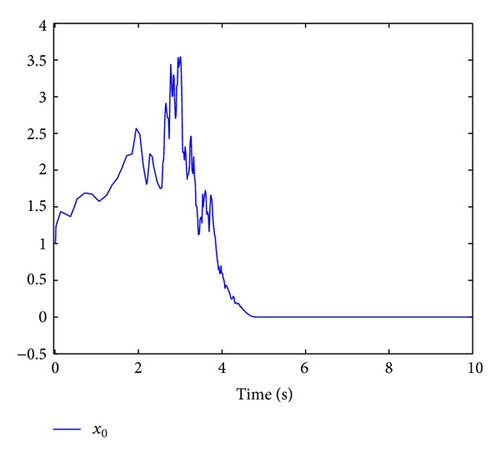
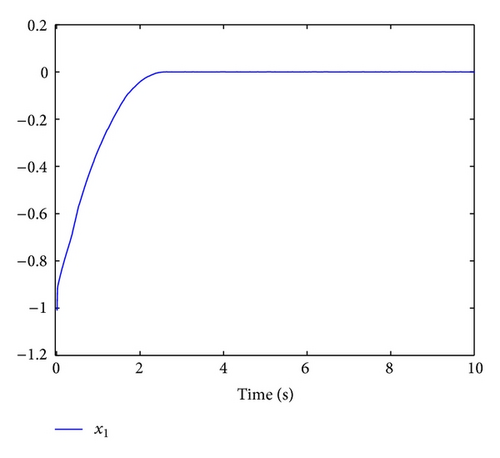
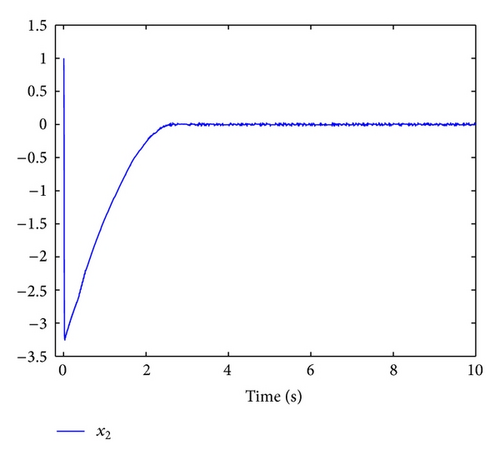
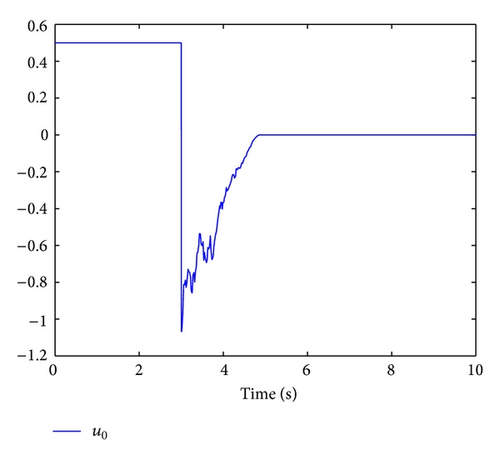
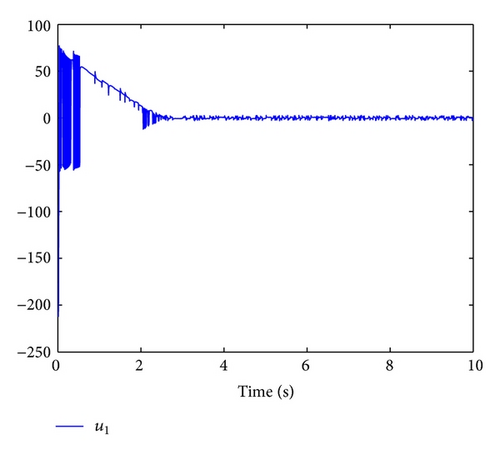
When (x₀(0), x₁(0), x₂(0)) = (1, −1,1), by choosing σ = 3 and l = 2/3, according to the design procedure proposed in Section 4, a state feedback stabilizing controller can be explicitly given. Using MATLAB, Figures 1 and 2 are obtained to exhibit the trajectories of the closed-loop system. From these figures, we can see that the states of the closed-loop system are finite time regulated to zero almost surely.

Details are in the caption following the image — **Figure 1 (a) x0**
Open in figure viewer PowerPoint

States of the closed-loop system.

6. Conclusion

In this paper, the finite-time state feedback stabilization problem has been investigated for a class of nonholonomic systems with more general stochastic disturbances. With the help of adding a power integrator technique, a systematic control design procedure is developed in the stochastic setting. It should be noted that the proposed controller can only work well when the whole state vector is measurable. Therefore, a natural and more interesting problem is how to design output feedback stabilizing controller for the system studied in the paper if only partial state vector is measurable, which is now under our further investigation.

Acknowledgments

This work has been supported in part by National Nature Science Foundation of China under Grants 61073065 and 61273091 and the Key Program of Science Technology Research of Education Department of Henan Province under Grant 13A120016. The authors thank the editor and the anonymous reviewers for their constructive comments and suggestions for improving the quality of the paper.

References

1 Brockett R. W., R. W. Brockett, R. S. Millman, and H. J. Sussmann, Asymptotic stability andfeed back stabilization, Differential Geometric Control Theory, 1983, 2961–2963.
Google Scholar
2 Astolfi A., Discontinuous control of nonholonomic systems, Systems & Control Letters. (1996) 27, no. 1, 37–45, https://doi.org/10.1016/0167-6911(95)00041-0, MR1375910, ZBL0877.93107.
10.1016/0167-6911(95)00041-0
Web of Science® Google Scholar
3 Xu W. L. and Huo W., Variable structure exponential stabilization of chained systems based on the extended nonholonomic integrator, Systems & Control Letters. (2000) 41, no. 4, 225–235, https://doi.org/10.1016/S0167-6911(00)00057-8, MR1830365, ZBL0980.93067.
10.1016/S0167-6911(00)00057-8
Web of Science® Google Scholar
4 Murray R. M. and Sastry S. S., Nonholonomic motion planning: steering using sinusoids, IEEE Transactions on Automatic Control. (1993) 38, no. 5, 700–716, https://doi.org/10.1109/9.277235, MR1224308, ZBL0800.93840.
10.1109/9.277235
Web of Science® Google Scholar
5 Jiang Z. P., Iterative design of time-varying stabilizers for multi-input systems in chained form, Systems & Control Letters. (1996) 28, no. 5, 255–262, https://doi.org/10.1016/0167-6911(96)00029-1, MR1413290, ZBL0866.93084.
10.1016/0167-6911(96)00029-1
Web of Science® Google Scholar
6 Tian Y. P. and Li S., Exponential stabilization of nonholonomic dynamic systems by smooth time-varying control, Automatica. (2002) 38, no. 8, 1139–1146, https://doi.org/10.1016/S0005-1098(01)00303-X, MR2133474, ZBL1003.93039.
10.1016/S0005-1098(01)00303-X
Web of Science® Google Scholar
7 Kolmanovsky I. and McClamroch N. H., Hybrid feedback laws for a class of cascade nonlinear control systems, IEEE Transactions on Automatic Control. (1996) 41, no. 9, 1271–1282, https://doi.org/10.1109/9.536497, MR1409472, ZBL0862.93048.
10.1109/9.536497
Web of Science® Google Scholar
8 Jiang Z. P., Robust exponential regulation of nonholonomic systems with uncertainties, Automatica. (2000) 36, no. 2, 189–209, https://doi.org/10.1016/S0005-1098(99)00115-6, MR1827775, ZBL0952.93057.
10.1016/S0005-1098(99)00115-6
Web of Science® Google Scholar
9 Xi Z., Feng G., Jiang Z. P., and Cheng D., A switching algorithm for global exponential stabilization of uncertain chained systems, IEEE Transactions on Automatic Control. (2003) 48, no. 10, 1793–1798, https://doi.org/10.1109/TAC.2003.817937, MR2021431.
10.1109/TAC.2003.817937
Web of Science® Google Scholar
10 Ge S. S., Wang Z., and Lee T. H., Adaptive stabilization of uncertain nonholonomic systems by state and output feedback, Automatica. (2003) 39, no. 8, 1451–1460, https://doi.org/10.1016/S0005-1098(03)00119-5, MR2141690, ZBL1038.93079.
10.1016/S0005-1098(03)00119-5
Web of Science® Google Scholar
11 Liu Y. G. and Zhang J. F., Output-feedback adaptive stabilization control design for non-holonomic systems with strong non-linear drifts, International Journal of Control. (2005) 78, no. 7, 474–490, https://doi.org/10.1080/00207170500080280, MR2147906.
10.1080/00207170500080280
Web of Science® Google Scholar
12 Xi Z., Feng G., Jiang Z. P., and Cheng D., Output feedback exponential stabilization of uncertain chained systems, Journal of the Franklin Institute. (2007) 344, no. 1, 36–57, https://doi.org/10.1016/j.jfranklin.2005.10.002, MR2305614, ZBL1119.93057.
10.1016/j.jfranklin.2005.10.002
Web of Science® Google Scholar
13 Zheng X. and Wu Y., Adaptive output feedback stabilization for nonholonomic systems with strong nonlinear drifts, Nonlinear Analysis. (2009) 70, no. 2, 904–920, https://doi.org/10.1016/j.na.2008.01.037, MR2468429, ZBL1152.93048.
10.1016/j.na.2008.01.037
Web of Science® Google Scholar
14 Gao F., Yuan F., and Yao H., Robust adaptive control for nonholonomic systems with nonlinear parameterization, Nonlinear Analysis. (2010) 11, no. 4, 3242–3250, https://doi.org/10.1016/j.nonrwa.2009.11.019, MR2661985, ZBL1214.93038.
10.1016/j.nonrwa.2009.11.019
Google Scholar
15 Liang Z. Y. and Wang C. L., Robust stabilization of nonholonomic chained form systems with uncertainties, Acta Automatica Sinica. (2011) 37, no. 2, 129–142, https://doi.org/10.3724/SP.J.1004.2011.00129, MR2848489, ZBL1240.70015.
10.3724/SP.J.1004.2011.00129
Google Scholar
16 Wang J., Gao H., and Li H., Adaptive robust control of nonholonomic systems with stochastic disturbances, Science in China F. (2006) 49, no. 2, 189–207, https://doi.org/10.1007/s11432-006-0189-5, MR2250882, ZBL1117.93027.
10.1007/s11432-006-0189-5
Web of Science® Google Scholar
17 Liu Y. L. and Wu Y. Q., Output feedback control for stochastic nonholonomic systems with growth rate restriction, Asian Journal of Control. (2011) 13, no. 1, 177–185, https://doi.org/10.1002/asjc.230, MR2809546, ZBL1248.93137.
10.1002/asjc.230
Web of Science® Google Scholar
18 Zhao Y., Yu J., and Wu Y., State-feedback stabilization for a class of more general high order stochastic nonholonomic systems, International Journal of Adaptive Control and Signal Processing. (2011) 25, no. 8, 687–706, https://doi.org/10.1002/acs.1233, MR2837225, ZBL1227.93100.
10.1002/acs.1233
PubMed Web of Science® Google Scholar
19 Bhat S. P. and Bernstein D. S., Continuous finite-time stabilization of the translational and rotational double integrators, IEEE Transactions on Automatic Control. (1998) 43, no. 5, 678–682, https://doi.org/10.1109/9.668834, MR1618028, ZBL0925.93821.
10.1109/9.668834
Web of Science® Google Scholar
20 Hong Y., Wang J., and Xi Z., Stabilization of uncertain chained form systems within finite settling time, IEEE Transactions on Automatic Control. (2005) 50, no. 9, 1379–1384, https://doi.org/10.1109/TAC.2005.854620, MR2164439.
10.1109/TAC.2005.854620
Web of Science® Google Scholar
21 Wang J., Zhang G., and Li H., Adaptive control of uncertain nonholonomic systems in finite time, Kybernetika. (2009) 45, no. 5, 809–824, MR2599114, ZBL1190.93086.
Web of Science® Google Scholar
22 Yin J., Khoo S., Man Z., and Yu X., Finite-time stability and instability of stochastic nonlinear systems, Automatica. (2011) 47, no. 12, 2671–2677, https://doi.org/10.1016/j.automatica.2011.08.050, MR2886936, ZBL1235.93254.
10.1016/j.automatica.2011.08.050
Web of Science® Google Scholar
23 Gao F. and Yuan F., Finite-time stabilization of stochastic nonholonomic systems and its application to mobile robot, Abstract and Applied Analysis. (2012) 18, 361269, MR2991020, ZBL1253.93087.
Google Scholar
24 Huang X., Lin W., and Yang B., Global finite-time stabilization of a class of uncertain nonlinear systems, Automatica. (2005) 41, no. 5, 881–888, https://doi.org/10.1016/j.automatica.2004.11.036, MR2157720, ZBL1098.93032.
10.1016/j.automatica.2004.11.036
CAS Web of Science® Google Scholar
25 Li J., Qian C., and Ding S., Global finite-time stabilisation by output feedback for a class of uncertain nonlinear systems, International Journal of Control. (2010) 83, no. 11, 2241–2252, https://doi.org/10.1080/00207179.2010.511658, MR2747289, ZBL1210.93064.
10.1080/00207179.2010.511658
Web of Science® Google Scholar
26 Qian C. and Lin W., A continuous feedback approach to global strong stabilization of nonlinear systems, IEEE Transactions on Automatic Control. (2001) 46, no. 7, 1061–1079, https://doi.org/10.1109/9.935058, MR1842139, ZBL1012.93053.
10.1109/9.935058
Web of Science® Google Scholar
27 Chen W. and Jiao L. C., Finite-time stability theorem of stochastic nonlinear systems, Automatica. (2010) 46, no. 12, 2105–2108, https://doi.org/10.1016/j.automatica.2010.08.009, MR2878238.
10.1016/j.automatica.2010.08.009
PubMed Web of Science® Google Scholar
28 Chen W. and Jiao L. C., Authors′ reply to comments on “Finite-time stability theorem of stochastic nonlinear systems” [Automatica 46 (2010) 2105–2108], Automatica. (2011) 47, no. 7, 1544–1545, MR2889258, 2-s2.0-79957494501, https://doi.org/10.1016/j.automatica.2011.02.053.
10.1016/j.automatica.2011.02.053
Web of Science® Google Scholar
29 Situ R., Thoery of Stochastic Differential Equations with Jumps and Applications: Mathematical and Analysis Techniques with Applications to Engineering, 2005, Springer, New York, NY, USA, MR2160585.
Google Scholar
30 Liu H. J. and Mu X. W., A converse lyapunov theorem for stochastic finite-time stability, Proceedings of the 30th Chinese Control Conference, 2011, 1419–1423.
Google Scholar
31 Polendo J. and Qian C., A generalized homogeneous domination approach for global stabilization of inherently nonlinear systems via output feedback, International Journal of Robust and Nonlinear Control. (2007) 17, no. 7, 605–629, https://doi.org/10.1002/rnc.1139, MR2314806, ZBL1113.93087.
10.1002/rnc.1139
Web of Science® Google Scholar
32 Yang B. and Lin W., Nonsmooth output feedback design with a dynamic gain for uncertain systems with strong nonlinearity, Proceedings of the 46th IEEE Conference on Decision and Control (CDC ′07), December 2007, New Orieans, La, USA, 3495–3500, 2-s2.0-62749189903, https://doi.org/10.1109/CDC.2007.4434846.
10.1109/CDC.2007.4434846
Google Scholar
33 Li W., Xie X. J., and Zhang S., Output-feedback stabilization of stochastic high-order nonlinear systems under weaker conditions, SIAM Journal on Control and Optimization. (2011) 49, no. 3, 1262–1282, https://doi.org/10.1137/100798259, MR2818881, ZBL1228.93101.
10.1137/100798259
Web of Science® Google Scholar
34 Qian C. and Lin W., Non-Lipschitz continuous stabilizers for nonlinear systems with uncontrollable unstable linearization, Systems & Control Letters. (2001) 42, no. 3, 185–200, https://doi.org/10.1016/S0167-6911(00)00089-X, MR2007048.
10.1016/S0167-6911(00)00089-X
Web of Science® Google Scholar

Citing Literature

All articles

Further Result on Finite-Time Stabilization of Stochastic Nonholonomic Systems

Abstract

1. Introduction

2. Notations and Preliminary Results

3. Problem Formulation

4. Finite-Time Control Design

5. Simulation Example

6. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Further Result on Finite-Time Stabilization of Stochastic Nonholonomic Systems

Abstract

1. Introduction

2. Notations and Preliminary Results

3. Problem Formulation

4. Finite-Time Control Design

5. Simulation Example

6. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Related

Information