Volume 2013, Issue 1 413529

Research Article

Open Access

A Modified Generalized Laguerre Spectral Method for Fractional Differential Equations on the Half Line

D. Baleanu

Department of Mathematics and Computer Sciences, Faculty of Arts and Sciences, Cankaya University, Eskisehir Yolu 29.Km, 06810 Ankara, Turkey cankaya.edu.tr

Department of Chemical and Materials Engineering, Faculty of Engineering, King Abdulaziz University, Jeddah 21589, Saudi Arabia kau.edu.sa

Institute of Space Sciences, Magurele-Bucharest, Romania spacescience.ro

Search for more papers by this author

A. H. Bhrawy,

A. H. Bhrawy

Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia kau.edu.sa

Department of Mathematics, Faculty of Science, Beni-Suef University, Beni-Suef 62511, Egypt bsu.edu.eg

Search for more papers by this author

T. M. Taha,

Corresponding Author

T. M. Taha

[email protected]

Department of Mathematics, Faculty of Science, Beni-Suef University, Beni-Suef 62511, Egypt bsu.edu.eg

Search for more papers by this author

D. Baleanu,

D. Baleanu

Department of Mathematics and Computer Sciences, Faculty of Arts and Sciences, Cankaya University, Eskisehir Yolu 29.Km, 06810 Ankara, Turkey cankaya.edu.tr

Department of Chemical and Materials Engineering, Faculty of Engineering, King Abdulaziz University, Jeddah 21589, Saudi Arabia kau.edu.sa

Institute of Space Sciences, Magurele-Bucharest, Romania spacescience.ro

Search for more papers by this author

A. H. Bhrawy,

A. H. Bhrawy

Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia kau.edu.sa

Department of Mathematics, Faculty of Science, Beni-Suef University, Beni-Suef 62511, Egypt bsu.edu.eg

Search for more papers by this author

T. M. Taha,

Corresponding Author

T. M. Taha

[email protected]

Department of Mathematics, Faculty of Science, Beni-Suef University, Beni-Suef 62511, Egypt bsu.edu.eg

Search for more papers by this author

First published: 26 August 2013

https://doi.org/10.1155/2013/413529

Citations: 20

Academic Editor: Soheil Salahshour

Share a link

Email
Wechat
Bluesky

Abstract

This paper deals with modified generalized Laguerre spectral tau and collocation methods for solving linear and nonlinear multiterm fractional differential equations (FDEs) on the half line. A new formula expressing the Caputo fractional derivatives of modified generalized Laguerre polynomials of any degree and for any fractional order in terms of the modified generalized Laguerre polynomials themselves is derived. An efficient direct solver technique is proposed for solving the linear multiterm FDEs with constant coefficients on the half line using a modified generalized Laguerre tau method. The spatial approximation with its Caputo fractional derivatives is based on modified generalized Laguerre polynomials with x ∈ Λ = (0, ∞), α > −1, and β > 0, and i is the polynomial degree. We implement and develop the modified generalized Laguerre collocation method based on the modified generalized Laguerre-Gauss points which is used as collocation nodes for solving nonlinear multiterm FDEs on the half line.

1. Introduction

Due to the fact that fractional calculus has extensive applications in chemistry, engineering, neuron modeling, and biological sciences, the use of fractional calculus has attracted great interest from the mathematical science research community (e.g., see [1–5]).

As is well known, spectral methods use orthogonal polynomials as the basis functions and so usually provide accurate numerical results, see [6–9] and the references therein. In particular, we could employ tau and pseudospectral modified generalized Laguerre approximations and interpolation to solve multiterm fractional differential equations on semi-infinite interval. However, some authors developed the modified generalized Laguerre spectral method for the half line for ordinary, partial, and delay differential equations, see [8, 10–12]. The Laguerre polynomials of fractional orders and its generalization can be expressed by the Bell polynomials, see [13–15].

Because of the difficulty in obtaining exact solutions to many fractional differential equations, there is a large number of papers dealing with the numerical solution of fractional differential equation [16–21]. The usual spectral methods based on Legendre, Chebyshev, and Jacobi polynomials are only available for bounded domains for the numerical solution of FDEs [22, 23]. In [22, 24, 25], the authors discussed the operational matrices of Caputo fractional derivatives of shifted Chebyshev and Jacobi polynomials with spectral techniques to provide numerical approximations to the solution of linear and nonlinear multiterm FDEs on finite intervals. Ahmadian et al. [26] applied the Jacobi operational matrix to present an efficient algorithm for solving a class of fuzzy FDEs. Li et al. [27] employed spectral approximations to compute the fractional integral and the Caputo derivative; they also presented pseudospectral approximation for a class of FDEs. Yüzbaşı [28] proposed Bessel collocation method for the approximate solution of the Bagley-Torvik equation. Atabakzadeh et al. [29] extended the application of the shifted Chebyshev operational matrix for obtaining an analytical approximation solution for linear and nonlinear multiorder FDE. Moreover, the authors of [30] extended the application of the Legendre operational matrix for treating the fractional order fuzzy differential equations. Recently, Bhrawy et al. [31, 32] proposed the operational matrices of Riemann-Liouville fractional integration of Chebyshev and modified generalized Laguerre polynomials which are employed together with spectral tau method for solving linear FDEs on finite and semi-infinite intervals, respectively.

The fundamental aim of this paper is to extend the application of spectral tau and collocation methods based on modified generalized Laguerre polynomials to solve the linear and nonlinear multiterm fractional initial value problems on the half line. We propose the modified generalized Laguerre spectral tau (MGLT) approximation for obtaining a direct solution technique to solve linear multiterm FDE on the half line. This method requires the Caputo fractional derivatives of any fractional order of the modified generalized Laguerre polynomials of any degree which is already stated and proved.

The modified generalized Laguerre spectral collocation (MGLC) approximation, which is more reliable, is employed to obtain approximate solution of nonlinear multiterm FDE on the half line with leading fractional differential operator of order ν (m − 1 < ν ≤ m) and m initial conditions. To be more precise, in such approximation, the nonlinear FDE is collocated only at (N − m + 1) zeros of modified generalized Laguerre polynomials. Therefore, the problem reduces to a system of (N + 1) nonlinear algebraic equations which may be solved by any standard technique to find the spectral solution u_N(x). To the best of the our knowledge, the proposed algorithms have not been introduced for the numerical solution of multiterm FDEs on the half line.

The plan of the paper is as follows. In the next section, we introduce basic properties of modified generalized Laguerre polynomials. In Section 3, the Caputo fractional derivative of the modified generalized Laguerre polynomials is proved. In Section 4, we develop modified generalized Laguerre tau and collocation spectral methods for solving multiterm FDEs. In Section 5, several numerical examples are implemented. Also, a conclusion is given in Section 6.

2. Properties of Modified Generalized Laguerre Polynomials

We recall below some relevant properties of the modified generalized Laguerre polynomials (see [8, 33, 34]).

Now, let Λ = (0, ∞) and w^(α,β)(x) = x^αe^−βx be a weight function on Λ in the usual sense. Define

()

equipped with the following inner product and norm:

()

Next, let

be the modified generalized Laguerre polynomial of degree i for α > −1 and β > 0, that is defined by

()

According to (2.3)-(2.4) of [11] for α > −1 and β > 0, we have

()

where

and

The set of modified generalized Laguerre polynomials is the

-orthogonal system, namely,

()

where δ_jk is the Kronecker function and h_k = Γ(k + α + 1)/β^α+1 k!.

The modified generalized Laguerre polynomials of degree i on the interval Λ, are given by

()

where

The special value

()

will be of important use later.

A function

may be expressed in terms of modified generalized Laguerre polynomials as

()

In particular applications, the modified generalized Laguerre polynomials up to degree N + 1 are considered. Then, we have

()

We now turn the modified generalized Laguerre-Gausstype quadratures, including modified generalized Laguerre-Gauss and Gauss-Radau interpolations [11, 34, 35]. Let

and

, 0 ≤ j ≤ i, be the zeros of

and

, respectively. They are arranged in ascending order. Denote

, (0 ≤ j ≤ i), Z = G, R, the corresponding Christoffel numbers such that

()

For the modified generalized Laguerre-Gauss weights, we have

()

For the Gauss-Radau weights, we have

()

Note that the earlier two types of quadratures have close relations,

()

3. The Fractional Derivatives of

In this section, we prove the following theorem for expressing explicitly the fractional order derivatives of the modified generalized Laguerre polynomials in terms of the modified generalized Laguerre polynomials themselves.

Lemma 1. Let be a modified generalized Laguerre polynomial; then

()

Theorem 2. The Caputo fractional derivative of order ν for modified generalized Laguerre polynomials is given by

()

where

()

Proof. With the aid of (7), the ν-order derivative of modified generalized Laguerre polynomials is

()

The approximation of x^k−ν by N + 1 terms of modified generalized Laguerre series yields

()

where b_j is given by

()

Thanks to (18)–(20), we can write

()

where

, and

()

4. Application of the Fractional Derivative of Modified Generalized Laguerre Polynomials

In this section, we consider spectral tau and collocation methods based on the fractional derivative of modified generalized Laguerre polynomials to solve numerically the linear and nonlinear multiterm FDEs on the half line.

4.1. Tau Method for Linear Multiterm FDEs

We apply the modified generalized Laguerre tau (MGLT) method for tackling the linear multiterm FDEs on the half line

()

subject to initial conditions

()

where γ_j (j = 1, …, k + 1) are constant coefficients, m − 1 < ν ≤ m, 0 < ζ₁ < ζ₂ < ⋯<ζ_k < ν. While D^νu(x) ≡ u^(ν)(x) is the ν-order fractional derivative of u(x), and g(x) is a source function.

The modified generalized Laguerre polynomials

form a complete orthogonal system in weighted space;

. Hence, we define

()

then the standard modified generalized Laguerre tau approximation to (23) is to find u_N ∈ S_N(Λ) such that

()

Let us denote

()

then (26) can be written as

()

Let us also denote

()

where

()

then by virtue of the orthogonality relation of modified generalized Laguerre polynomials (6) and making use of (8) and (16) and after some manipulation, we may deduce that the elements of a_kj,

, s = 1,2, …, r − 1, and c_kj are given by

()

Therefore, (28) can be written in the following matrix form:

()

4.2. Collocation Method for Nonlinear Multiterm FDEs

It is known that the collocation method approximates differential equations in physical space, so it is easy to apply to various problems, including variable coefficient and nonlinear differential equations (see, for instance, [36]). In this section, an algorithm for solving fractional differential equation is proposed based on modified generalized Laguerre spectral collocation (MGLC) method in a half line. Here, we study the following multiterm FDE:

()

with initial conditions

()

where the fractional order derivatives are taken to be of the Caputo type, m − 1 < ν ≤ m, 0 < β₁ < β₂ < ⋯<β_k < ν, and F is a nonlinear function.

We now derive an efficient algorithm for solving nonlinear multiterm FDEs (33)-(34). We expand the numerical approximation in terms of modified generalized Laguerre polynomials

()

By virtue of (16), the fractional derivatives

can be expressed explicitly in terms of the expansion coefficients a_j.

The modified generalized Laguerre spectral collocation method for solving approximately (33), (34) is to find u_N(x) ∈ S_N(Λ) such that

()

is collocated at x_N−m+1,k, k = 0,1, …, N − m. In other words, we have to collocate (36) at the (N − m + 1) modified generalized Laguerre roots x_N−m+1,k, which immediately yields

()

with (33) written in the form

()

Finally, the problem is reduced to solve a system of (N + 1) nonlinear algebraic equations, (37)-(38), in the unknown expansion coefficients {a_j; j = 0,1, …, N}, which can be solved by Newton’s iteration method.

5. Numerical Results

We report in this section some numerical results obtained with the proposed algorithms in the previous section. Several test examples are implemented to ensure the effectiveness of the proposed methods for fractional differential equations in the half line.

Example 3. This example concerns a class of Bagley-Torvik equation given by the initial value problem

()

The solution is u(x) = x³.

This equation arises in the treatment of the motion of a large thin plate immersed in a Newtonian fluid. For the numerical solution of the Bagley-Torvik equation, see [37–41]. The solution of this problem is obtained by applying the modified generalized Laguerre tau method and the right-hand side is treated by modified generalized Laguerre-Gauss (G) and modified generalized Laguerre-Gauss-Radau (GR) quadratures with general parameters α and β. The maximum absolute errors obtained by MGLT method for various choices of N, α, and β are given in Figures 1 and 2. Moreover, the approximate solutions obtained by the proposed method for α = 0, β = 2, and two choices of N are shown in Figure 3 to make it easier to compare with the analytic solution.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Maximum absolute error by using MGLT (Gauss) with the various choices of N.

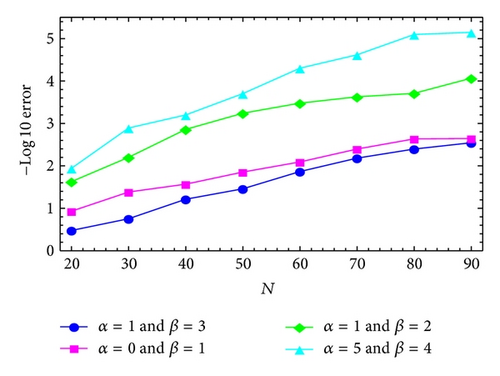
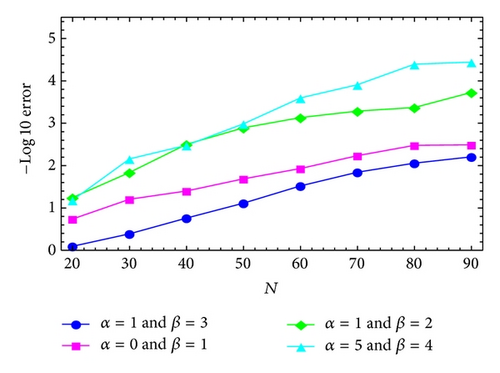
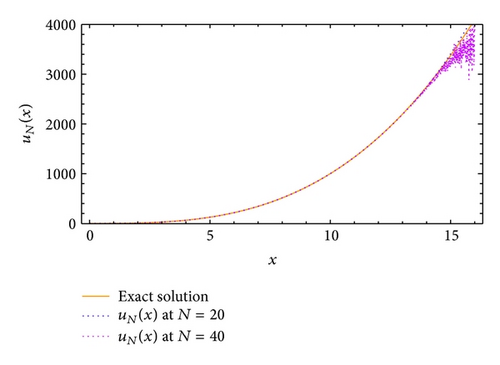
Example 4. Consider the equation

()

where

()

and the exact solution is given by u(x) = x⁴ − (1/2)x³ (see Table 1).

Table 1. Maximum absolute error, with various choices of N, for Example 4 in which x ∈ [0,10].

N	α	β	ν	MGLT(G)	MGLT(GR)	ν	MGLT(G)	MGLT(GR)	ν	MGLT(G)	MGLT(GR)
10	0	2	0.1	1.32 · 10⁻²	2.24 · 10⁻²	0.5	8.48 · 10⁻²	1.41 · 10⁻¹	0.99	6.54 · 10⁻³	1.07 · 10⁻²
30				1.35 · 10⁻⁴	1.78 · 10⁻⁴		1.37 · 10⁻³	1.82 · 10⁻³		1.84 · 10⁻⁴	2.53 · 10⁻⁴
50				1.96 · 10⁻⁵	2.47 · 10⁻⁵		2.45 · 10⁻⁴	3.14 · 10⁻⁴		4.30 · 10⁻⁵	5.71 · 10⁻⁵
70				3.41 · 10⁻⁶	4.20 · 10⁻⁶		4.86 · 10⁻⁵	6.10 · 10⁻⁵		7.03 · 10⁻⁶	9.16 · 10⁻⁶

10	4	3	0.1	4.54 · 10⁻³	1.67 · 10⁻²	0.5	2.36 · 10⁻²	8.98 · 10⁻²	0.99	1.43 · 10⁻³	5.85 · 10⁻³
30				2.86 · 10⁻⁶	8.06 · 10⁻⁶		2.73 · 10⁻⁵	8.33 · 10⁻⁵		2.96 · 10⁻⁶	1.03 · 10⁻⁵
50				8.61 · 10⁻⁸	2.37 · 10⁻⁷		1.22 · 10⁻⁶	3.54 · 10⁻⁶		1.72 · 10⁻⁷	5.72 · 10⁻⁷
70				1.81 · 10⁻⁸	5.12 · 10⁻⁸		2.10 · 10⁻⁷	6.53 · 10⁻⁷		3.30 · 10⁻⁸	1.19 · 10⁻⁷

10	6	4	0.1	4.92 · 10⁻³	2.27 · 10⁻²	0.5	2.77 · 10⁻²	1.33 · 10⁻¹	0.99	8.80 · 10⁻³	1.67 · 10⁻³
30				2.83 · 10⁻⁶	1.01 · 10⁻⁵		2.71 · 10⁻⁵	1.06 · 10⁻⁴		3.00 · 10⁻⁶	1.35 · 10⁻⁵
50				7.88 · 10⁻⁸	2.73 · 10⁻⁷		5.48 · 10⁻⁷	2.19 · 10⁻⁶		6.94 · 10⁻⁸	3.25 · 10⁻⁷
70				1.49 · 10⁻⁸	5.30 · 10⁻⁸		1.74 · 10⁻⁷	6.87 · 10⁻⁷		2.72 · 10⁻⁸	1.26 · 10⁻⁷

Example 5. We next consider the following:

()

where

()

and the exact solution is given by u(x) = cos (γx).

The solution of this problem is obtained by applying the technique described in Section 4. The maximum absolute error for γ = {0.1 and 0.01} and various choices of N, α, β, and ν are shown in Tables 2 and 3; moreover, the right-hand side is treated by modified generalized Laguerre Gauss and modified generalized Laguerre-Gauss-Radau quadratures.

Table 2. Maximum absolute error for γ = 1/10, with various choices of N, for Example 5 in which x ∈ [0,10].

N	α	β	ν	MGLT(G)	MGLT(GR)	ν	MGLT(G)	MGLT(GR)	ν	MGLT(G)	MGLT(GR)
10	0	1	1.5	7.97 · 10⁻⁴	2.47 · 10⁻³	0.9	7.28 · 10⁻⁵	1.40 · 10⁻⁴	0.5	1.10 · 10⁻⁴	1.89 · 10⁻⁴
30				1.38 · 10⁻⁴	3.81 · 10⁻⁴		7.11 · 10⁻⁶	1.21 · 10⁻⁵		7.36 · 10⁻⁶	1.11 · 10⁻⁵
50				4.02 · 10⁻⁵	1.09 · 10⁻⁴		1.51 · 10⁻⁶	2.49 · 10⁻⁶		1.29 · 10⁻⁶	1.88 · 10⁻⁶
70				2.51 · 10⁻⁵	6.64 · 10⁻⁵		3.79 · 10⁻⁷	6.15 · 10⁻⁷		5.86 · 10⁻⁷	8.41 · 10⁻⁷

10	2	2	1.5	5.39 · 10⁻⁴	4.44 · 10⁻³	0.9	6.29 · 10⁻⁵	2.78 · 10⁻⁴	0.5	9.84 · 10⁻⁵	3.54 · 10⁻⁴
30				1.33 · 10⁻⁵	9.33 · 10⁻⁵		8.65 · 10⁻⁷	3.20 · 10⁻⁶		9.31 · 10⁻⁷	2.77 · 10⁻⁶
50				4.26 · 10⁻⁶	3.00 · 10⁻⁵		1.99 · 10⁻⁷	7.37 · 10⁻⁷		1.71 · 10⁻⁷	5.06 · 10⁻⁷
70				1.78 · 10⁻⁶	1.22 · 10⁻⁵		7.56 · 10⁻⁸	2.72 · 10⁻⁷		5.28 · 10⁻⁸	1.52 · 10⁻⁷

10	5	3	1.5	1.19 · 10⁻⁴	1.87 · 10⁻³	0.9	1.67 · 10⁻⁵	1.34 · 10⁻⁴	0.5	2.93 · 10⁻⁵	1.86 · 10⁻⁴
30				2.25 · 10⁻⁶	3.48 · 10⁻⁵		1.58 · 10⁻⁷	1.09 · 10⁻⁶		1.76 · 10⁻⁷	1.02 · 10⁻⁶
50				1.28 · 10⁻⁶	1.92 · 10⁻⁵		5.85 · 10⁻⁸	3.33 · 10⁻⁷		5.97 · 10⁻⁸	3.33 · 10⁻⁷
70				8.52 · 10⁻⁷	1.26 · 10⁻⁵		3.21 · 10⁻⁸	2.30 · 10⁻⁷		2.81 · 10⁻⁸	1.54 · 10⁻⁷

Table 3. Maximum absolute error for γ = 1/100, with various choices of N, for Example 5 in which x ∈ [0,10].

N	α	β	ν	MGLT(G)	MGLT(GR)	ν	MGLT(G)	MGLT(GR)	ν	MGLT(G)	MGLT(GR)
10	0	1	1.5	7.97 · 10⁻⁶	2.47 · 10⁻⁵	0.9	7.28 · 10⁻⁷	1.40 · 10⁻⁶	0.5	1.10 · 10⁻⁶	1.89 · 10⁻⁶
30				1.38 · 10⁻⁶	3.81 · 10⁻⁶		7.11 · 10⁻⁸	1.21 · 10⁻⁷		7.39 · 10⁻⁸	1.11 · 10⁻⁷
50				4.02 · 10⁻⁷	1.09 · 10⁻⁶		1.51 · 10⁻⁸	2.49 · 10⁻⁸		1.29 · 10⁻⁸	1.88 · 10⁻⁸
70				2.51 · 10⁻⁷	6.64 · 10⁻⁷		3.79 · 10⁻⁹	6.15 · 10⁻⁹		5.86 · 10⁻⁹	8.41 · 10⁻⁹

10	2	2	1.5	5.39 · 10⁻⁶	4.44 · 10⁻⁵	0.9	6.29 · 10⁻⁷	2.78 · 10⁻⁶	0.5	9.85 · 10⁻⁷	3.54 · 10⁻⁶
30				1.33 · 10⁻⁷	9.33 · 10⁻⁷		8.65 · 10⁻⁹	3.20 · 10⁻⁸		9.31 · 10⁻⁹	2.77 · 10⁻⁸
50				4.26 · 10⁻⁸	3.00 · 10⁻⁷		2.00 · 10⁻⁹	7.37 · 10⁻⁹		1.71 · 10⁻⁹	5.06 · 10⁻⁹
70				1.78 · 10⁻⁸	1.22 · 10⁻⁷		7.56 · 10⁻¹⁰	2.72 · 10⁻⁹		5.28 · 10⁻¹⁰	1.52 · 10⁻⁹

10	5	3	1.5	1.19 · 10⁻⁶	1.87 · 10⁻⁵	0.9	1.67 · 10⁻⁷	1.34 · 10⁻⁶	0.5	2.94 · 10⁻⁷	1.87 · 10⁻⁶
30				2.25 · 10⁻⁸	3.48 · 10⁻⁷		1.58 · 10⁻⁹	1.09 · 10⁻⁸		1.76 · 10⁻⁹	1.02 · 10⁻⁸
50				1.28 · 10⁻⁸	1.92 · 10⁻⁷		5.85 · 10⁻¹⁰	4.27 · 10⁻⁹		5.97 · 10⁻¹⁰	3.33 · 10⁻⁹
70				8.52 · 10⁻⁹	1.26 · 10⁻⁷		3.21 · 10⁻¹⁰	2.30 · 10⁻⁹		2.81 · 10⁻¹⁰	1.53 · 10⁻⁹

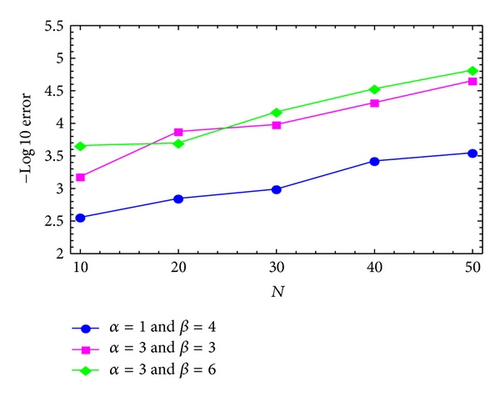
Example 6. We consider the equation

()

subject to

()

The analytic solution of this problem is u(x) = x² − x, we study two different cases of a, b, c, e, k, ν₁, ν₂, and ν.

(I)
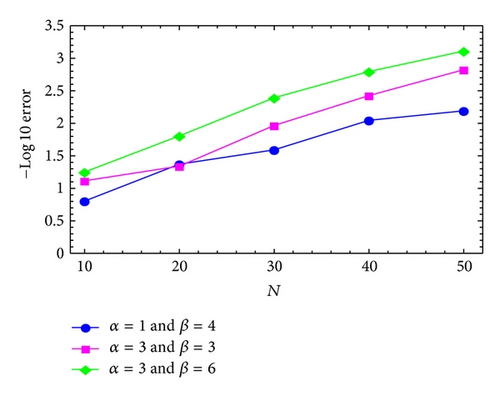
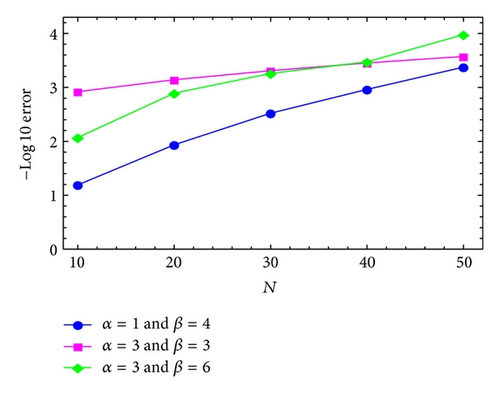
Regarding a = 1, b = 1, c = 1, e = 1, ν₁ = 0.77, ν₂ = 1.44, and ν = 3.91, Figures 4 and 5 display the maximum absolute errors using MGLT method with the treatment of right-hand side by modified generalized Laguerre-Gauss and Gauss-Radau, respectively.
(II)
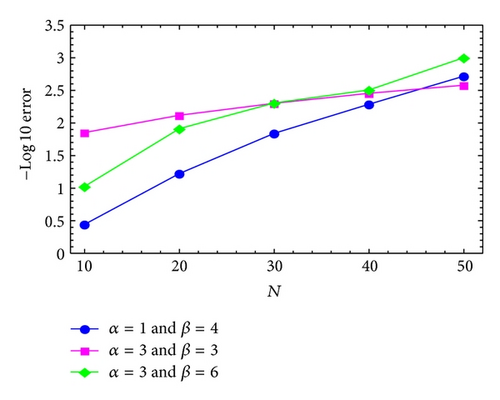
Regarding a = 1, b = 1, c = 0.5, e = 0.5, , , and , Figures 6 and 7 display the maximum absolute errors using MGLT method with the treatment of right-hand side by modified generalized Laguerre-Gauss and Gauss-Radau, respectively.

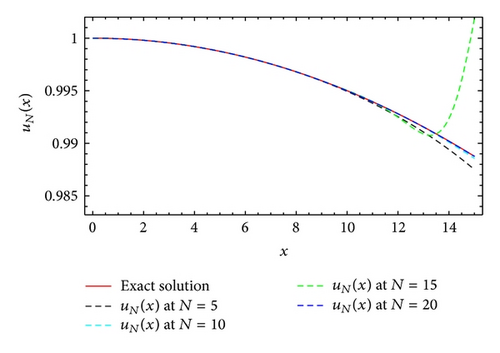
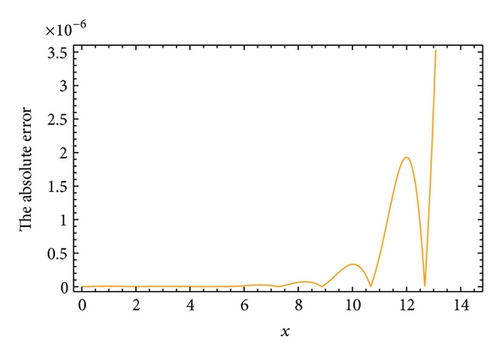
Example 7. Consider the Bagley-Torvik equation with boundary conditions

()

where

()

and the exact solution is given by u(x) = x⁵ − (29x⁴/10)+(76x³/25)−(339x²/250)+(27x/125).

Bagley-Torvik equation involving fractional derivative of order 3/2 arises in the modeling of the motion of a rigid plate in a Newtonian fluid and a gas in a fluid. We solve this equation with two-point boundary conditions where a = 1, b = 8/17, and c = 13/51 by using modified generalized Laguerre-Gauss and Gauss-Radau quadratures with general parameters α and β. The maximum absolute errors obtained by MGLT method for various choices of N, α, and β are given in Table 4. Moreover, the numerical and exact solutions obtained by the proposed method for α = 2, β = 4, and two choices of N are shown in Figures 8-9 to make it easier to compare with the analytic solution.

Table 4. Maximum absolute error for ν = 3/2, with various choices of N, for Example 5 in which x ∈ (0,1).

N	α	β	MGLT(G)	MGLT(GR)	α	β	MGLT(G)	MGLT(GR)
8	0	1	1.69 · 10⁻³	3.14 · 10⁻³	3	4	8.98 · 10⁻⁵	8.21 · 10⁻⁴
16			9.97 · 10⁻⁴	2.35 · 10⁻³			1.98 · 10⁻⁵	1.91 · 10⁻⁴
32			1.57 · 10⁻⁴	3.50 · 10⁻⁴			8.50 · 10⁻⁶	7.89 · 10⁻⁵
64			3.52 · 10⁻⁵	9.97 · 10⁻⁵			3.81 · 10⁻⁶	3.72 · 10⁻⁵

8	4	5	6.47 · 10⁻⁵	7.07 · 10⁻⁴	5	5	8.61 · 10⁻⁵	1.02 · 10⁻³
16			1.53 · 10⁻⁵	1.76 · 10⁻⁴			2.07 · 10⁻⁵	2.63 · 10⁻⁴
32			6.40 · 10⁻⁶	7.31 · 10⁻⁵			6.17 · 10⁻⁶	8.06 · 10⁻⁵
64			3.02 · 10⁻⁶	3.57 · 10⁻⁵			3.19 · 10⁻⁶	4.37 · 10⁻⁵

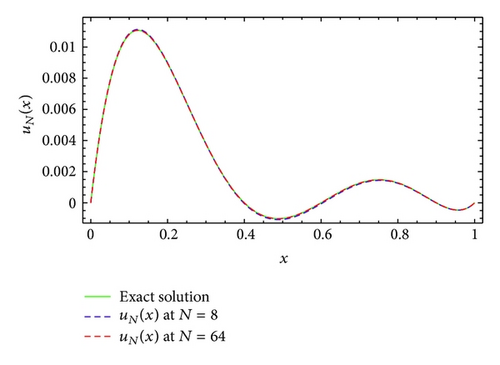
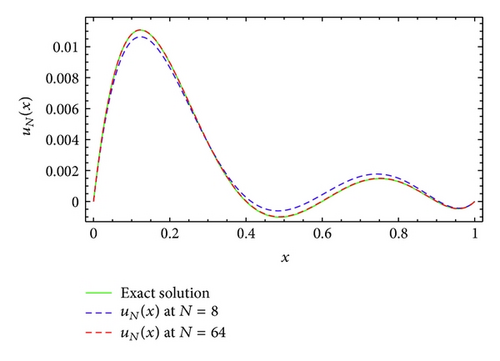
Example 8. We next consider the following nonlinear initial value problem:

()

where

()

and the exact solution is given by u(x) = cos (γx).

The solution of this problem is obtained by applying the modified generalized Laguerre collocation method. The approximate solution obtained by the proposed method for γ = 0.01, α = 2, β = 2, and two choices of N is shown in Figure 10 to make it easier to compare with the analytic solution. Moreover, the absolute error for γ = 0.01, α = 2, β = 2, and N = 20 is given in Figure 11.

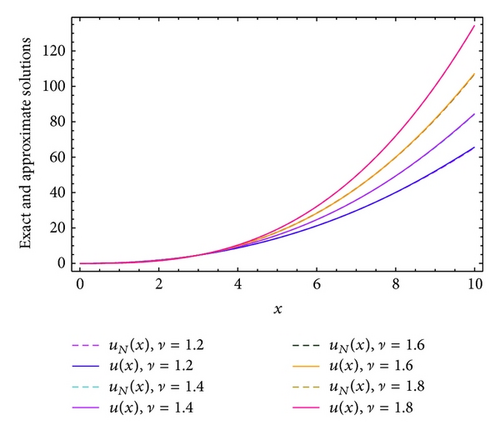
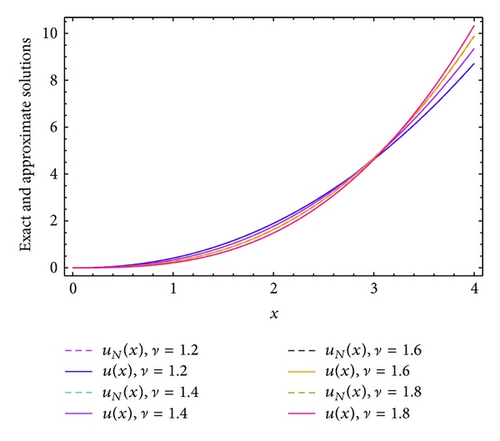
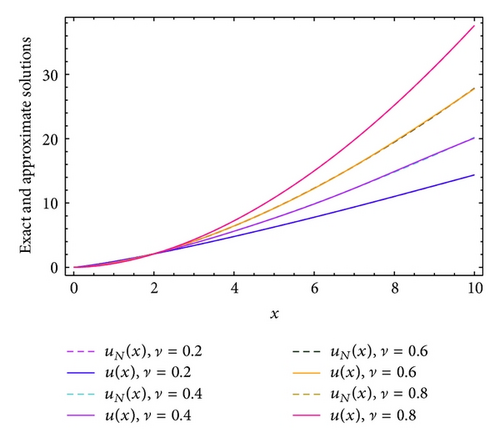
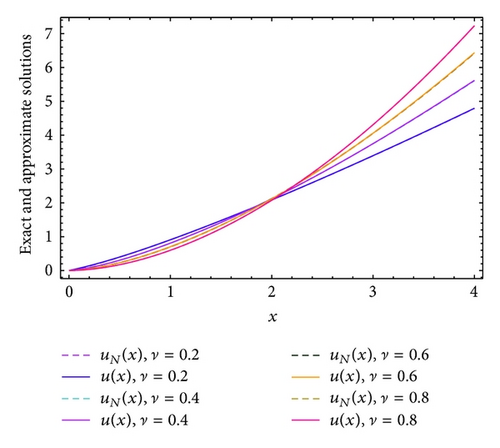
Example 9. Consider the following nonlinear initial value problem:

()

whose exact solution is given by u(x) = (1/Γ(ν + 2))x^ν+1.

Comparison between the curves of exact solutions and the approximate solutions at α = 0 and β = 1 of proposed problem subject to u(0) = u^′(0) = 0 for the four different fractional orders ν = 1.2, 1.4, 1.6, and 1.8 in case of N = 12 and N = 16 are shown in Figures 12 and 13, respectively. The maximum absolute errors at ν = 1.5 for various choices of α, β, and N in the interval [0,1] are shown in Table 5. Moreover, Figures 14 and 15 display a comparison between the curves of exact solutions and the approximate solutions at α = 0 and β = 1 of proposed problem subject to u(0) = 0 for the four different fractional orders ν = 0.2, 0.4, 0.6, and 0.8 in case of N = 12 and N = 16, respectively. From all the Figures 12–15, it can be seen that the numerical solutions are in complete agreement with the exact solutions for all values of ν. Also, from the numerical results implemented in this example, the classical Laguerre polynomial (α = 0, β = 1), which is used most frequently in practice, is not the best one, especially when we are approximating the solution of fractional differential equations.

Table 5. Maximum absolute error for ν = 3/2, with various choices of N, for Example 9 in which x ∈ (0,1).

N	α	β	MGLC	α	β	MGLC
3	0	1	2.66 · 10⁻²	2	3	2.61 · 10⁻²
6			2.27 · 10⁻³			3.04 · 10⁻³
9			1.30 · 10⁻³			1.36 · 10⁻³
12			5.68 · 10⁻⁴			7.52 · 10⁻⁴

3	2	4	1.39 · 10⁻²	3	6	1.07 · 10⁻²
6			1.87 · 10⁻³			1.86 · 10⁻³
9			8.47 · 10⁻⁴			6.94 · 10⁻⁴
12			4.02 · 10⁻⁴			3.63 · 10⁻⁴

6. Conclusions

In this paper, we have proposed two efficient spectral methods based on modified generalized Laguerre polynomials for tackling linear and nonlinear FDEs on the half line. In these methods, the problem is reduced to the solution of a system of algebraic equations in the expansion coefficient of the solution. Numerical examples were given to demonstrate the validity and applicability of the method. The computational results show that the proposed methods can be effectively used in numerical solution of time-dependent fractional partial differential equation and other problems on the half line.

References

1 Baleanu D., Diethelm K., Scalas E., and Trujillo J. J., Fractional Calculus Models and Numerical Methods, 2012, World Scientific, Singapore, Complexity, Nonlinearity and Chaos.
10.1142/8180
Google Scholar
2 Miller K. and Ross B., An Introduction to the Fractional Calaulus and Fractional Differential Equations, 1993, John Wiley & Sons, New York, NY, USA.
Google Scholar
3 Ortigueira M., Introduction to fraction linear systems. Part 1: continuous-time case, 147, IEE Proceedings Vision, Image, Signal Processing, 2000, 6–70.
Google Scholar
4 Oldham K. and Spanier J., The Fractional Calculus, 1974, Academic Press, New York, NY, USA.
Google Scholar
5 Kilbas A. A., Srivastava H. M., and Trujillo J. J., Theory and Applications of Fractional Differential Equations, 2006, 204, Elsevier, Amsterdam, The Netherlands, MR2218073.
10.1016/S0304-0208(06)80001-0
Google Scholar
6 Canuto C., Hussaini M. Y., Quarteroni A., and Zang T. A., Spectral Methods Fundamentals in Single Domains, 2006, Springer, Berlin, Germany, MR2223552.
10.1007/978-3-540-30726-6
Google Scholar
7 Doha E. H., Bhrawy A. H., Baleanu D., and Ezz-Eldien S. S., On shifted Jacobi spectral approximations for solving fractional differential equations, Applied Mathematics and Computation. (2013) 219, no. 15, 8042–8056, https://doi.org/10.1016/j.amc.2013.01.051, MR3037516.
10.1016/j.amc.2013.01.051
Web of Science® Google Scholar
8 Yan J.-P. and Guo B.-Y., A collocation method for initial value problems of second-order ODEs by using Laguerre functions, Numerical Mathematics. Theory, Methods and Applications. (2011) 4, no. 2, 283–295, MR2862671.
10.4208/nmtma.2011.42s.9
Web of Science® Google Scholar
9 Doha E. H. and Bhrawy A. H., An efficient direct solver for multidimensional elliptic Robin boundary value problems using a Legendre spectral-Galerkin method, Computers & Mathematics with Applications. (2012) 64, no. 4, 558–571, https://doi.org/10.1016/j.camwa.2011.12.050, MR2948602.
10.1016/j.camwa.2011.12.050
Web of Science® Google Scholar
10 Funaro D., C. Brezinski, L. Gori, and A. Ronveaux, Estimates of Laguerre spectral projectors in Sobolev spaces, Orthogonal Polynomials and Their Applications, 1991, Scientific Publishing, Singapore, 263–266.
Google Scholar
11 Guo B.-Y., Wang L.-L., and Wang Z.-Q., Generalized Laguerre interpolation and pseudospectral method for unbounded domains, SIAM Journal on Numerical Analysis. (2006) 43, no. 6, 2567–2589, https://doi.org/10.1137/04061324X, MR2206448.
10.1137/04061324X
Web of Science® Google Scholar
12 Gülsu M., Gürbüz B., Öztürk Y., and Sezer M., Laguerre polynomial approach for solving linear delay difference equations, Applied Mathematics and Computation. (2011) 217, no. 15, 6765–6776, https://doi.org/10.1016/j.amc.2011.01.112, MR2775723.
10.1016/j.amc.2011.01.112
Web of Science® Google Scholar
13 Schimming R. and Rida S. Z., Noncommutative Bell polynomials, International Journal of Algebra and Computation. (1996) 6, no. 5, 635–644, https://doi.org/10.1142/S0218196796000362, MR1419136.
10.1142/S0218196796000362
Google Scholar
14 El-Sayed A. M. A. and Rida S. Z., Bell polynomials of arbitrary (fractional) orders+, Applied Mathematics and Computation. (1999) 106, no. 1, 51–62, https://doi.org/10.1016/S0096-3003(98)10088-7, MR1714101.
10.1016/S0096-3003(98)10088-7
Web of Science® Google Scholar
15 Van Gorder R. A., Computation of certain infinite series of the form Σf(n)n^k for arbitrary real-valued k, Applied Mathematics and Computation. (2009) 215, no. 3, 1209–1216, https://doi.org/10.1016/j.amc.2009.06.064, MR2568978.
10.1016/j.amc.2009.06.064
Web of Science® Google Scholar
16 Shahriyar B., Ismail F., Aghabeigi S., Ahmadian A., and Salahshour S., An eigenvalueeigenvector method for solving a system of fractional differential equations with uncertainty, Mathematical Problems in Engineering. (2013) 2013, 11, 579761.
10.1155/2013/579761
Web of Science® Google Scholar
17 Bhrawy A. H., Tharwat M. M., and Yildirim Y., A new formula for fractional integrals of Chebyshev polynomials: application for solving multi-term fractional differential equations, Applied Mathematical Modelling. (2012) 37, no. 6, 4245–4252.
10.1016/j.apm.2012.08.022
Web of Science® Google Scholar
18 Jiang Y.-L. and Ding X.-L., Waveform relaxation methods for fractional differential equations with the Caputo derivatives, Journal of Computational and Applied Mathematics. (2013) 238, 51–67, https://doi.org/10.1016/j.cam.2012.08.018, MR2972589.
10.1016/j.cam.2012.08.018
Web of Science® Google Scholar
19 Kazem S., Abbasbandy S., and Kumar S., Fractional-order Legendre functions for solving fractional-order differential equations, Applied Mathematical Modelling. Simulation and Computation for Engineering and Environmental Systems. (2013) 37, no. 7, 5498–5510, MR3020667.
Google Scholar
20 Song J., Yin F., Cao X., and Lu F., Fractional variational iteration method versus Adomian′s decomposition method in some fractional partial differential equations, Journal of Applied Mathematics. (2013) 2013, 10, 392567, MR3032203.
10.1155/2013/392567
Google Scholar
21 Zhang X., Liu L., Wu Y., and Lu Y., The iterative solutions of nonlinear fractional differential equations, Applied Mathematics and Computation. (2013) 219, no. 9, 4680–4691, https://doi.org/10.1016/j.amc.2012.10.082, MR3001516.
10.1016/j.amc.2012.10.082
Web of Science® Google Scholar
22 Bhrawy A. H., Alofi A. S., and Ezz-Eldien S. S., A quadrature tau method for fractional differential equations with variable coefficients, Applied Mathematics Letters. (2011) 24, no. 12, 2146–2152, https://doi.org/10.1016/j.aml.2011.06.016, MR2826154.
10.1016/j.aml.2011.06.016
Web of Science® Google Scholar
23 Doha E. H., Bhrawy A. H., and Ezz-Eldien S. S., Efficient Chebyshev spectral methods for solving multi-term fractional orders differential equations, Applied Mathematical Modelling. (2011) 35, no. 12, 5662–5672, https://doi.org/10.1016/j.apm.2011.05.011, MR2820942.
10.1016/j.apm.2011.05.011
Web of Science® Google Scholar
24 Doha E. H., Bhrawy A. H., and Ezz-Eldien S. S., A Chebyshev spectral method based on operational matrix for initial and boundary value problems of fractional order, Computers & Mathematics with Applications. (2011) 62, no. 5, 2364–2373, https://doi.org/10.1016/j.camwa.2011.07.024, MR2831698.
10.1016/j.camwa.2011.07.024
Web of Science® Google Scholar
25 Doha E. H., Bhrawy A. H., and Ezz-Eldien S. S., A new Jacobi operational matrix: an application for solving fractional differential equations, Applied Mathematical Modelling. (2012) 36, no. 10, 4931–4943, https://doi.org/10.1016/j.apm.2011.12.031, MR2930392.
10.1016/j.apm.2011.12.031
Web of Science® Google Scholar
26 Ahmadian A., Suleiman M., Salahshour S., and Baleanu D., A Jacobi operational matrix for solving a fuzzy linear fractional differential equation, Advances in Difference Equations. 2013, article 104, https://doi.org/10.1186/1687-1847-2013-104.
10.1186/1687-1847-2013-104
PubMed Google Scholar
27 Li C., Zeng F., and Liu F., Spectral approximations to the fractional integral and derivative, Fractional Calculus and Applied Analysis. (2012) 15, no. 3, 383–406, https://doi.org/10.2478/s13540-012-0028-x, MR2944106.
10.2478/s13540-012-0028-x
Web of Science® Google Scholar
28 Yüzbaşı S., Numerical solution of the Bagley-Torvik equation by the Bessel collocation method, Mathematical Methods in the Applied Sciences. (2013) 36, no. 3, 300–312, https://doi.org/10.1002/mma.2588, MR3022970.
10.1002/mma.2588
Web of Science® Google Scholar
29 Atabakzadeh M. H., Akrami M. H., and Erjaee G. H., Chebyshev operational matrix method for solving multi-order fractional ordinary differential equations, Applied Mathematical Modelling. (2013) https://doi.org/10.1016/j.apm.2013.04.019.
10.1016/j.apm.2013.04.019
Web of Science® Google Scholar
30 Ahmadian A., Suleiman M., and Salahshour S., An operational matrix based on Legendre polynomials for solving fuzzy fractional-order differential equations, Abstract and Applied Analysis. (2013) 2013, 29, https://doi.org/10.1155/2013/505903, 505903.
10.1155/2013/505903
Google Scholar
31 Bhrawy A. H. and Alofi A. S., The operational matrix of fractional integration for shifted Chebyshev polynomials, Applied Mathematics Letters. (2013) 26, no. 1, 25–31, https://doi.org/10.1016/j.aml.2012.01.027, MR2971394.
10.1016/j.aml.2012.01.027
Web of Science® Google Scholar
32 Bhrawy A. H., Alghamdi M., and Taha T. M., A new modified generalized Laguerre operational matrix of fractional integration for solving fractional differential equations on the half line, Advances in Difference Equations. (2012) 2012.
10.1186/1687-1847-2012-179
PubMed Google Scholar
33 Guo B.-Y. and Zhang X.-Y., A new generalized Laguerre spectral approximation and its applications, Journal of Computational and Applied Mathematics. (2005) 181, no. 2, 342–363, https://doi.org/10.1016/j.cam.2004.12.008, MR2146844.
10.1016/j.cam.2004.12.008
Web of Science® Google Scholar
34 Szegő G., Orthogonal Polynomials, 1985, 23, American Mathematical Society. Colloquium Publications.
Google Scholar
35 Guo B.-Y. and Zhang C., The spectral method for high order problems with proper simulations of asymptotic behaviors at infinity, Journal of Computational and Applied Mathematics. (2013) 237, no. 1, 269–294, https://doi.org/10.1016/j.cam.2012.08.009, MR2966905.
10.1016/j.cam.2012.08.009
Web of Science® Google Scholar
36 Bhrawy A. H. and Alofi A. S., A Jacobi-Gauss collocation method for solving nonlinear Lane-Emden type equations, Communications in Nonlinear Science and Numerical Simulation. (2012) 17, no. 1, 62–70, https://doi.org/10.1016/j.cnsns.2011.04.025, MR2825987.
10.1016/j.cnsns.2011.04.025
Web of Science® Google Scholar
37 Diethelm K. and Ford N. J., Numerical solution of the Bagley-Torvik equation, BIT. Numerical Mathematics. (2002) 42, no. 3, 490–507, MR1931882.
10.1023/A:1021973025166
Web of Science® Google Scholar
38 Ray S. S. and Bera R. K., Analytical solution of the Bagley Torvik equation by Adomian decomposition method, Applied Mathematics and Computation. (2005) 168, no. 1, 398–410, https://doi.org/10.1016/j.amc.2004.09.006, MR2170841.
10.1016/j.amc.2004.09.006
Web of Science® Google Scholar
39 Çenesiz Y., Keskin Y., and Kurnaz A., The solution of the Bagley-Torvik equation with the generalized Taylor collocation method, Journal of the Franklin Institute. (2010) 347, no. 2, 452–466, https://doi.org/10.1016/j.jfranklin.2009.10.007, MR2593729.
10.1016/j.jfranklin.2009.10.007
Web of Science® Google Scholar
40 Raja M. A. Z., Khan J. A., and Qureshi I. M., Solution of fractional order system of Bagley-Torvik equation using evolutionary computational intelligence, Mathematical Problems in Engineering. (2011) 2011, 18, 675075, https://doi.org/10.1155/2011/675075, MR2781559.
10.1155/2011/675075
Web of Science® Google Scholar
41 Ray S. S., On Haar wavelet operational matrix of general order and its application for the numerical solution of fractional Bagley Torvik equation, Applied Mathematics and Computation. (2012) 218, no. 9, 5239–5248, https://doi.org/10.1016/j.amc.2011.11.007, MR2870045.
10.1016/j.amc.2011.11.007
Web of Science® Google Scholar

Citing Literature

All articles

A Modified Generalized Laguerre Spectral Method for Fractional Differential Equations on the Half Line

Abstract

1. Introduction

2. Properties of Modified Generalized Laguerre Polynomials

3. The Fractional Derivatives of

4. Application of the Fractional Derivative of Modified Generalized Laguerre Polynomials

4.1. Tau Method for Linear Multiterm FDEs

4.2. Collocation Method for Nonlinear Multiterm FDEs

5. Numerical Results

6. Conclusions

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Modified Generalized Laguerre Spectral Method for Fractional Differential Equations on the Half Line

Abstract

1. Introduction

2. Properties of Modified Generalized Laguerre Polynomials

3. The Fractional Derivatives of

4. Application of the Fractional Derivative of Modified Generalized Laguerre Polynomials

4.1. Tau Method for Linear Multiterm FDEs

4.2. Collocation Method for Nonlinear Multiterm FDEs

5. Numerical Results

6. Conclusions

References

Citing Literature

Figures

References

Related

Information