Robust Backstepping Control for Cold Rolling Main Drive System with Nonlinear Uncertainties
Abstract
The nonlinear model of main drive system in cold rolling process, which considers the influence with parameter uncertainties such as clearance and variable friction coefficient, as well as external disturbance by roll eccentricity and variation of strip material quality, is built. By transformation, the lower triangular structure form of main drive system is obtained. The backstepping algorithm based on signal compensation is proposed to design a linear time-invariant (LTI) robust controller, including a nominal controller and a robust compensator. A comparison with PI controller shows that the controller has better disturbance attenuation performance and tracking behaviors. Meanwhile, according to its LTI characteristic, the robust controller can be realized easily; therefore it is also appropriated to high speed dynamic rolling process.
1. Introduction
The main drive system in cold rolling mill, as a high accuracy mechanical-electrical system, plays an important role in high speed stable rolling operation. However, the torsional vibration which usually occurs in main drive system has been recognized as a major restriction to the increase of strip yield and improvement of product quality [1, 2]. It may lead to large gauge variations [3] of strip as well as the instability of rolling speed and can even cause damage to the mechanical equipment of mill stands [4, 5]. As a matter of fact, the phenomenon of vibration exists generally in rolling process, but the time and location of where it happens cannot be easily predicted. Moreover, there are many factors that can cause the occurrence of torsional vibration, such as unstable state of friction in rolling deformation zone [6], asynchronous working between upper and lower work rolls [7], defects or failure in reduction gear box [8], influence of high order electrical harmonics excitation [9], and so on. Thus, all of these factors will cause a huge difficulty to operators on vibration-related fault detection [10–13] and suppression [14]. In order to analyze and control torsional vibration, many researchers have done a lot of work in studying the chatter mechanism. Although these mechanisms, such as negative damping effect and model matching have been identified after years of research, no clear and definite theory of their mechanics has emerged. One of the most important factors responsible for this situation is the oversimplified by neglecting nonlinearities in mechanical-electrical system, then the models can hardly be suitable for the vibration mechanism and the further control algorithms designation. Variable stiffness due to clearance in gearbox and friction coefficient should me most concerned among these nonlinearities, since the existence of nonlinear friction and stiffness terms have become the obstacle to modifying system dynamic characteristics.
In addition to studying vibration mechanism in main drive system with the consideration of nonlinearity, the control strategy is also a key point in vibration suppression. With the higher demand on speed and accuracy in modern cold rolling process, the traditional control method, such as PID, has not been qualified to manage those vibration pheromones, and some advanced control algorithms [15, 16] are not suitable to deal with the problem of model nonlinearity in rolling process. Thus, a nonlinear control algorithm is necessary to deal with this situation.
One of the recent breakthroughs in nonlinear control theory is the introduction of backstepping algorithms. The relative-degree constraints over parameterization and growth condition are removed by allowing the controlled plant to be nonlinearly dependent on structure uncertainty, such as unknown parameters or unmodeled time-varying disturbances [17–20]. Although there are many advantages in backstepping algorithm, the “explosion of complexity” problem [18, 21], caused by repeated differentiation, cannot be ignored due to its increase in calculation complexity, therefore making severe time delay on control output, which can directly influence the operation performance in cold rolling mills. In this paper, a more general case is discussed, where uncertainties are not required to satisfy matching condition or to be smooth, and then a robust control method based backstepping algorithm is introduced. The feature of this approach is that the designed controller is an LTI one, so the controller can be easily realized, and then the “explosion of complexity” can be avoided.
The major objective pursued in this paper is to formulate a reasonable nonlinear model with parameter uncertainty and external disturbance of cold rolling main drive system, including variable stiffness by clearance, changeable friction coefficient due to relative speed between work roll and strip, and external disturbance by load variation under dynamic working conditions. Furthermore, after proper model transformation, a robust backstepping control algorithm is stated. Finally, within actual industrial data, simulation result shows the good performance and tracking behaviors of this proposed approach, even under the influence of parameter uncertainties and external disturbances.
2. Problem Description
2.1. Mathematical Model of Main Drive System
Based on our former research, the main drive system of cold rolling mill can be defined as a “Mass-Spring System”, including motor, shaft, gearbox, roll, and so on. Reasonable simplification is necessary for a better analysis of the dynamic behaviors in rolling system, which makes two parts of main drive system, mass system such as motor, as well as roll and spring system like gearbox and shaft. Therefore, the two-degrees-of-freedom model within clearance, nonlinear friction coefficient, and load disturbance is established in this section. The dynamic structure of main drive system is shown in Figure 1, where J1, J2 is the moment of inertia of motor and load, M1 is the drive torque of motor, M2 is the torque of load with load disturbance, K12 is defined as torsional stiffness coefficient of flexible shaft, C1, is the damping coefficient of motor, rolls, and shaft separately, θ1 is the rotational angle of motor, and θ2 is the rotational angle of work roll.
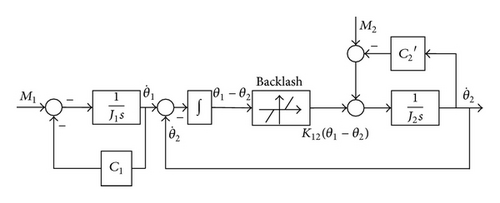
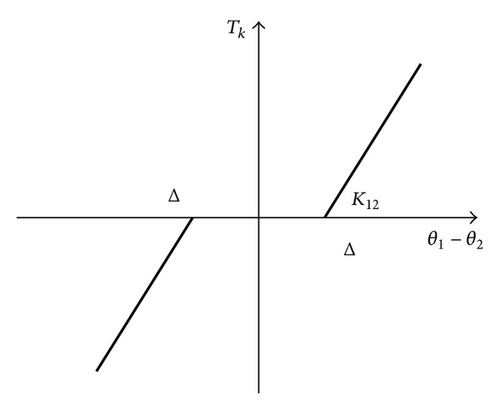
2.2. Model Transformation
2.3. Control Task
3. Control Design Procedure
It is expected we will design a linear robust controller within backstepping procedure, which can produce a control input u(t) to drive the output yp(t) of the plant to track a reference output, denoted by yd(t).
- (1)
firstly, the tracking problem is transformed into a regulation problem;
- (2)
then the nominal controller is designed to get desired property for the nominal disturbance-free model;
- (3)
thirdly, the influence of the uncertainties and external disturbance is regarded as an equivalent disturbance;
- (4)
finally, a robust compensator is designed to restrain the effect of the equivalent disturbance and to achieve robust properties.
Step 1. To start, define the variables below:
Based on (16), can be designed as
In order to attenuate and suppress the influence of subsystem robust property by equivalent disturbance, the robust compensating input is constructed as follows
As shown in (21), if the filter time-constant f1 is positive and sufficiently large, we can see that F1(s) is sufficiently small, then one can expect that f1w1(t) would approximate and neutralize the effect of equivalent disturbance to gain robust property.
Since is immeasurable, it can be expressed in the form
To get the robust compensating input w1(t), only is needed in the form below:
According to those equations above, the subsystem can be established as
As the second step, the item of subsystem (24) will be considered as disturbance and continue the similar design procedure.
Step i. Consider the ith subsystem (i = 2, …, n − 1)
Introduce the error variable
And regard as the virtual control input of the ith subsystem
The robust compensating input wi(t) can be expressed as
Note that
Therefore, wi(t) can also be given by
After differentiating , one has
Step n. At the last step, one has
The real control input u(t) can be constructed including nominal control input and robust compensating input
Note that
wn(t) can be expressed as
As we can see from (34) and (36), it follows that
After summarizing the design results, the following system structure can be established:
The whole controller description is
4. Simulation Result and Discussion
From the design procedure of the control algorithm in the last section, one can notice that the problem of “explosion of complexity” is fully avoided. Meanwhile, less information about reference output as well as the bounds of uncertainties is applied to construct the robust controller. While the price of this solution is that when there is no dynamic uncertainty or external disturbance, the tracking error cannot be guaranteed to converge to zero, it can only be made as small as desired by appropriately choosing controller parameters αi and fi. However, due to the actual situation in industrial fields, uncertainty and external disturbance are ubiquitous in dynamic rolling process, especially when the vibration phenomenon begins to emerge. Besides, from (9)–(11), one can notice the good applicability of our approach on the mathematical model in main drive system with the consideration of model parametric nonlinearity and external load disturbance.
In order to prove the advantage of control method, a simulation experiment with actual industrial data is built, because the torsional vibration in tandem cold rolling mill usually happens in the latter roll-stand, due to its higher rolling speed and the influence by back tension variations. Therefore, the experimental parameters come from the main drive system data in 4th rolling stand of Baosteel. The major parameters are listed in Table 1.
| Parameters | Value and unit |
|---|---|
| J1 | 1552 kg·m2 |
| J2 | 1542 kg·m2 |
| K12 | 5.93 × 106 N·M/rad |
| Δ | 0.1 rad |
| R | 0.4 m |
| P | 932 KN |
| c | 0.06 |
| d | 0.0024 |
Based on the results on robust property and selection of control performance index in [20], the two key parameters can be obtained separately: αi = 3 (i = 1,2, 3), f1 = 10, f2 = 100, and f3 = 1000. Let us assume that the operation condition of dynamic rolling mill neglects the influence of load disturbance temporarily, while the parameter uncertainty by variable nonlinear stiffness and friction is considered. Given the system, a unit step response with rolling speed r = 30 rad/s, as shown in Figure 3, although the PI controller is capable of maintaining stable rolling operation in ideal working conditions, which means the system response is not affected by variation of strip thickness or by back or front tension, it is no longer qualified in this situation as its overshoot and regulating time is unacceptable in real industrial rolling process. On the other hand, the control performance of robust backstepping algorithm is still good because of its better suppression capability on parameter uncertainties.
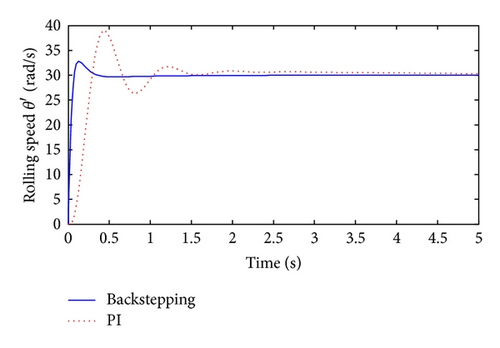
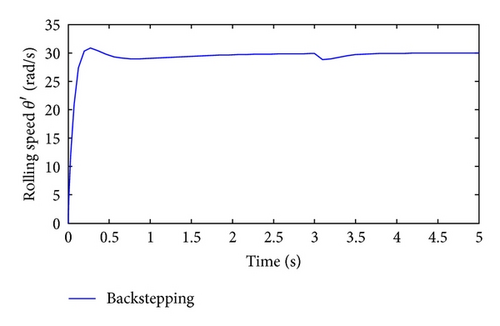
Figure 4 shows the system step response when the load disturbance was added at 3 s. During a short-term fluctuation, the system under robust backstepping algorithm returns to normal status quickly, mainly because of low-pass filter and robust compensating input on the attenuation to equivalent disturbance.
5. Conclusion
A nonlinear model of cold rolling main drive system has been formulated, including variable stiffness by clearance, changeable friction coefficient with consideration of relative speed between work roll and strip, and the load disturbance with roll eccentricity and variation of strip material quality.
In view of parameter uncertainty and external disturbance in dynamic cold rolling process, the mathematical model is transformed into a lower triangular structure. A robust backstepping method has been introduced to design a robust controller, which contains a nominal controller and a robust compensator, to achieve a robust tracking property for real controlled plant. The simulation results show its good performance on reference signal tracking under different operational conditions. Meanwhile, its linear and time-invariant characteristic causes the controller to be fulfilled easily.
Despite these encouraging results, the industrial application of this control algorithm should be involved. Due to the existing difficulty, such as nonlinearity, strong coupling features in rolling mill system, and requirement in fast response on control algorithm, the improvements of controller on efficiency and practically would be enormous benefits. Moreover, the possibility for expansion of this robust controller in industrial practical plants to improve strip quality is recommended as an important issue for future investigation.
Acknowledgments
The authors gratefully acknowledge the support by National Natural Science Foundation of China (nos. 51205018 and 61074085), Research Projects of State Key Laboratory of Mechanical System and Vibration (no. MSV-2014-09), China Postdoctoral Science Foundation Funded Project (no. 2012M510321), and Fundamental Research Funds for the Central Universities (nos. FRF-TP-12-104A and FRF-SD-12-008B). Meanwhile, great thanks also goes to Baosteel Company in Shanghai, China, for data support, and the anonymous reviewers for their valuable comments and suggestions.




