On the First-Order Shape Derivative of the Kohn-Vogelius Cost Functional of the Bernoulli Problem
Abstract
The exterior Bernoulli free boundary problem is being considered. The solution to the problem is studied via shape optimization techniques. The goal is to determine a domain having a specific regularity that gives a minimum value for the Kohn-Vogelius-type cost functional while simultaneously solving two PDE constraints: a pure Dirichlet boundary value problem and a Neumann boundary value problem. This paper focuses on the rigorous computation of the first-order shape derivative of the cost functional using the Hölder continuity of the state variables and not the usual approach which uses the shape derivatives of states.
1. Introduction
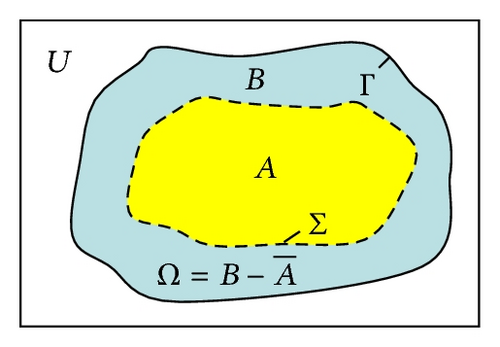
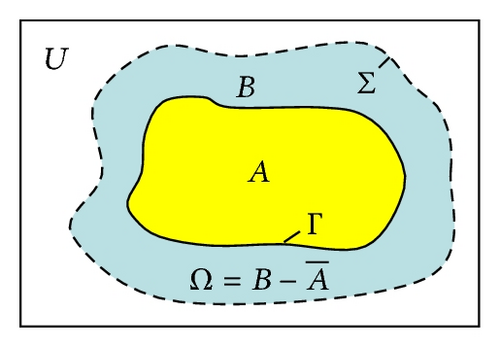
The Bernoulli problem is the prototype of a stationary free boundary problem. It arises in various applications such as electrochemical machining, potential flow in fluid mechanics, tumor growth, optimal insulation, molecular diffusion, and steel and glass production [1–6]. A characteristic feature of free boundary problems is that not only the state variable is unknown but also the domain on which the state equation is posed. This represents a significant theoretical as well as numerical challenge. One can characterize the Bernoulli problem, at least along general lines, by finding a connected domain as well as a function which is harmonic on this domain. One component on the boundary is known. The other one is determined by a set of overdetermined boundary conditions (a Dirichlet condition and a Neumann condition) for the state. If the free boundary component is strictly exterior to the fixed part of the boundary, the problem is called exterior Bernoulli problem and interior Bernoulli problem otherwise. For more discussions related to interior and exterior Bernoulli problems, we refer the reader to [1, 4, 7–10].
Recent strategies to compute a numerical solution are based on reformulating the Bernoulli problem as a shape optimization problem. This can be achieved in several ways. For a given domain, one can choose one of the boundary conditions on the free boundary to obtain a well-posed state equation. The domain is determined by the requirement that the other condition on the free boundary is satisfied in a least squares sense (cf. [11–13]). Alternatively, one can compute on a given domain two auxiliary states: uD which satisfies the Dirichlet condition and uN which satisfies the Neumann condition on the free boundary. The underlying domain is selected such that the difference is as small as possible. In fact, if J(Ω) = 0 for a domain Ω then uD = uN and (uD, Ω) is a solution of the Bernoulli problem. Sometimes J is called Kohn-Vogelius functional since Kohn and Vogelius were among the first who used such a functional in the context of inverse problems [14]. Standard algorithms to minimize J require some gradient information. So in this paper, the first-order sensitivity analysis is carried out for the functional J for the exterior Bernoulli problem. The main contribution in this paper is the application of a shape optimization technique that leads to the explicit expression for the shape derivative of the cost functional. This is done through variational means similar to the techniques developed in [9, 10, 13], wherein we use the Hölder continuity of the state variables satisfying the Dirichlet and Neumann problems but we do not introduce any adjoint variables. In our approach, we also bypass the use of the material derivatives of the states (which was done in [1]) and the use of states’ shape derivatives.
The rest of the paper is structured as follows. Section 2 presents the Bernoulli free boundary problem and its shape optimization formulations. Section 3 provides a list of shape optimization tools that are needed in the analysis for the shape derivatives of the Kohn-Vogelius cost functional J. Section 4 presents an exhaustive discussion on the first-order shape derivative of J. Finally, Section 5 draws conclusion and observation.
2. The Bernoulli Problem
- (1)
Tracking Neumann data [11, 12] as
()where the state function uD is the solution to the Dirichlet problem() - (2)
Tracking Dirichlet data [11, 13] as
()where the state function uN is the solution to the Neumann problem() - (3)
Minimizing the Kohn-Vogelius type cost functional [12, 15] as
()where state functions uD and uN satisfy (4) and (6), respectively.
In this paper, we are just interested in the study of minimizing the Kohn-Vogelius functional J.
3. Tools in Shape Optimization
3.1. Feasible Domain Ω
In this work, we are interested in Ck,1-domains, where k ≥ 0. Aside from being Ck,1 we also assume that these are bounded and connected subsets of a bigger set U which is also a bounded connected Ck,1 domain. This U is called the universal or the hold-all domain. The smoothness of these domains can be defined in the following sense (cf. [16]).
Definition 1. A domain Ω ⊂ ℝn with a nonempty boundary ∂Ω is called a Ck,l-domain, where 0 ≤ k, 0 < l ≤ 1, if for every y ∈ ∂Ω there exists a neighborhood Ny of y and a Ck,l diffeomorphism fy : Ny → B(0,1) such that (a) fy(Ny∩Ω) = B+(0,1), (b) fy(Ny∩∂Ω) = B0(0,1), and .
To illustrate this for n = 2 and k = l = 1, see Figure 2.
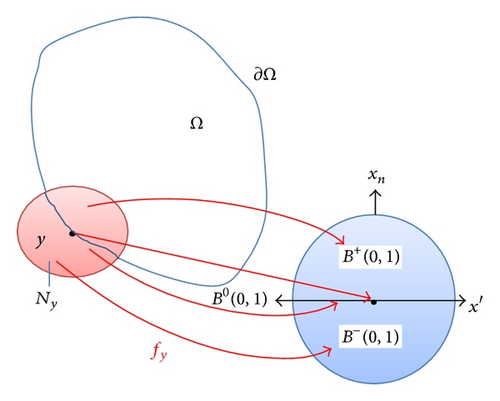
Note that if Ω is a bounded, open, connected set with a C0,1 boundary, then . This was given in [17] and we prove it as follows.
Theorem 2 (see [17].)If Ω is a bounded open connected subset of ℝn with Lipschitz continuous boundary, then .
Proof. The interior of is the largest open set contained in the set . Moreover, . It follows that . Next, we show that . Clearly, . We now show that if , then x ∉ ∂Ω.
Suppose x ∈ ∂Ω and . We need to show that any open set N containing x contains an element not in . We first note that by definition of C0,1 domain, there exists a neighborhood Nx of x ∈ ∂Ω and a diffeomorphism fx : Nx → B(0,1). Let N be an open set containing x with N ⊂ Nx. It follows that fx(N) is an open set containing 0 and this set is contained in B(0,1). Hence, there exists z ∈ fx(N) such that z ∈ B−(0,1). This implies that . Thus, N contains an element not in , which is a contradiction. Therefore, . We have proven that if x ∈ ∂Ω, then . Taking the contrapositive of this statement we get that if , then x ∉ ∂Ω. Since but x ∉ ∂Ω, we conclude x ∈ Ω. Thus, . We have shown that and . Therefore, .
3.2. The Perturbation of Identity Technique
The main objective in this subsection is to show that Tt is a diffeomorphism from Ω to Ωt for sufficiently small t. To verify this, we need the following results, which are given and proven in [17].
Theorem 3. If Ω is a bounded, open, connected set in ℝn such that and φ is a continuous injective mapping from to ℝn, then
Theorem 4. Suppose
- (1)
Ω is a bounded, open, connected set in ℝn such that ,
- (2)
where φ0 is injective,
- (3)
such that
()
- (i)
is a homeomorphism (i.e., φ is a bijection, φ is continuous, and φ−1 is continuous),
- (ii)
φ : Ω → φ(Ω) is a C1-diffeomorphism (i.e., φ is a bijection, φ ∈ C1(Ω), φ−1 ∈ C1(φ(Ω))),
- (iii)
φ(Ω) = φ0(Ω), .
We also consider the following property of a domain, which is also found in [17, page 52].
Lemma 5. If Ω is a bounded, open, connected subset of ℝn having a Lipschitz continuous boundary, then there is a number c(Ω) such that, for any given points , one can find a finite sequence of points yk, k = 1, …, l + 1, satisfying the following properties:
- (a)
y1 = x, yk ∈ Ω for 2 ≤ k ≤ l, yl+1 = y,
- (b)
(yk, yk+1) ⊂ Ω for 1 ≤ k ≤ l,
- (c)
.
Lemma 6 (see [9], [13].)Consider the operator Tt defined by (9), where V ∈ Θ, which is described by (13). Then
- (i)
It = 1 + t div V + t2det DV,
- (ii)
there exist tV, α1, α2 > 0 such that 0 < α1 ≤ It(x) ≤ α2, for |t | ≤ tV, x ∈ U.
Proof. In general, for n-dimensional case, the Jacobian of Tt is given by DTt = (aij), where aij = t(∂Vi/∂xj) if, i ≠ j, and aii = 1 + t(∂Vi/∂xi). By definition of the determinant, we can write det DTt as
This verifies (i). To show (ii) we first get the lower bound for It(x). Take
Considering the theorems and lemmas presented beforehand, we are now ready to prove the following theorem.
Theorem 7. Let Ω and U be nonempty bounded open connected subsets of ℝ2 with Lipschitz continuous boundaries, such that , and ∂Ω is the union of two disjoint boundaries Γ and Σ. Let Tt be defined as in (9) where V belongs to Θ, defined as (13).
Then for sufficiently small t,
- (1)
is a homeomorphism,
- (2)
Tt : U → U is a C1,1 diffeomorphism, and in particular, Tt : Ω → Ωt is a C1,1 diffeomorphism,
- (3)
Γt = Tt(Γ) = Γ,
- (4)
∂Ωt = Γ ∪ Tt(Σ).
Proof. First, because U is a C0,1 domain, it follows that by Theorem 2. Second, , and it is injective. Third, it is evident that Tt is C1,1 because V is C1,1. For x ∈ ∂U, Tt(x) = x because V vanishes on ∂U. For x ∈ U, the determinant of the Jacobian of the perturbation of identity operator Tt is given by (19). By Lemma 6, there exists a tV > 0, given by (20), such that det DTt(x) > 0 for all x ∈ U and for |t | ≤ tV. Hence, by applying Theorem 4, we conclude that Tt(U) = U and for all |t | < tV, and is a homeomorphism. Furthermore, by Theorem 4, we find that Tt : U → U is a C1 diffeomorphism. To show that Tt is a C1,1 diffeomorphism, we are left to show that is Lipschitz continuous. To verify this we use Lemma 5.
Given any two points u, v ∈ U we choose {yk} such that properties (a)–(c) of Lemma 5 are satisfied. For fixed |t| < tV, differentiating the identities and will lead to
This implies
Applying the infinity norm in the space C(X; ℝ2) we have
Since DTt is Lipschitz continuous, we have
Corollary 8. Let Ω and U be two domains of ℝ2 with C1,1 boundary. Then for |t | < tV, where tV is given by (20), the perturbed domain Ωt : = Tt(Ω) is also of class C1,1.
Proof. Given y ∈ ∂Ωt, we let . Then there exists a neighborhood Nx of x and a diffeomorphism gx ∈ C1,1(Nx, B(0,1)) such that gx(Nx∩Ω) = B+(0,1), gx(Nx∩∂Ω) = B0(0,1), and gx(Nx∩Ωc) = B−(0,1). We have also shown that Tt defined in Theorem 7 is a C1,1 diffeomorphism. Since is continuous, is a neighborhood of y in U. Define . This is bijective because gx and are bijective. gy ∈ C1,1(Ny, B(0,1)) because (hence ) and gx ∈ C1,1(Nx, B(0,1)). Also, .
Next, we note that ∂Ωt∩Ny = Tt(∂Ω)∩Ny = Tt(∂Ω)∩Tt(Nx). Since Tt is injective, we have ∂Ωt∩Ny = Tt(∂Ω∩Nx). Thus by definition of gy we get
This shows that Ωt is indeed of class C1,1.
Remark 9. Theorem 7 and Corollary 8 tell us that the reference Ω and the perturbed domain Ωt have the same topological structure and regularity under the perturbation of identity operator Tt for sufficiently small t. See Figure 3 for illustration.
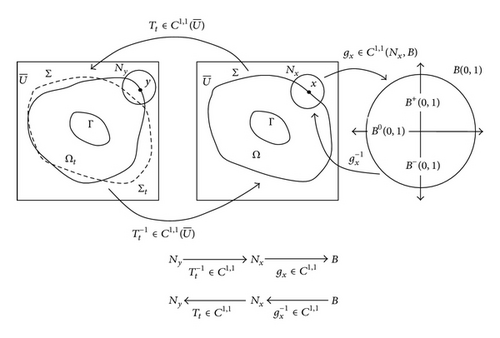
Remark 10. We note the following observations for fixed, sufficiently small t.
- (1)
.
- (2)
.
- (3)
.
- (4)
wt ∈ C(Σ; ℝ).
- (5)
implies that |V|∞ and |DV|∞ are both finite.
We now provide several properties of Tt.
Lemma 11 (see [9], [13], [16], [18].)Consider the transformation Tt, where the fixed vector field V belongs to Θ, defined in (13). Then there exists tV > 0 such that Tt and the functions in (16) and (31) restricted to the interval IV = (−tV, tV) have the following regularity and properties.
- (1)
.
- (2)
.
- (3)
.
- (4)
t ↦ wt ∈ C1(IV, C(Σ)).
- (5)
.
- (6)
There is β > 0 such that At(x) ≥ βI for x ∈ U.
- (7)
(d/dt)Tt|t=0 = V.
- (8)
.
- (9)
(d/dt)DTt|t=0 = DV.
- (10)
(d/dt)(DTt) −1|t=0 = −DV.
- (11)
(d/dt)It|t=0 = div V.
- (12)
(d/dt)At|t=0 = (div V)I − (DV + (DV) T) ≡ A.
- (13)
lim t→0wt = 1.
- (14)
(d/dt)wt|t=0 = div ΣV,
We provide proofs for properties (3) and (8). The rest can be seen in [19].
Proof. (3) Suppose , t, h ∈ IV, and . Then
- (i)
y1 = Tt(y), yk ∈ U for 2 ≤ k ≤ l, yl+1 = Th(y),
- (ii)
(yk, yk+1) ⊂ U for 1 ≤ k ≤ l,
- (iii)
,
To show that is continuous from IV to , we only need to show that for every t ∈ IV, whenever |t − h| < δ and h ∈ IV. Let . Using (37), estimate as follows:
Proof of property (8) in Lemma 11 is as follows. Given , we have . This implies that
3.3. The Method of Mapping
If u is defined in Ω and ut is defined in Ωt, then the direct comparison of ut with u is generally not possible since the functions are defined on different domains. To overcome this difficulty, one maps ut back to Ω by composing it with Tt; that is, one defines ut∘Tt : Ω → ℝ. With this new mapping one can define the material and the shape derivatives of states, the domain and boundary integral transformations, and derivatives of integrals, as well as the Eulerian derivative of the shape functional. This technique is called the method of mapping.
Material and Shape Derivatives. The material and shape derivatives of state variables are defined as follows [20, 21].
Definition 12. Let u be defined in [0, tV] × U. An element , called the material derivative of u, is defined as
if the limit exists in (Hk(Ω)).
Remark 13. The material derivative can be written as
Definition 14. Let u be defined in [0, tV] × U. An element u′ ∈ Hk(Ω) is called the shape derivative of u at Ω in the direction V, if the following limit exists in Hk(Ω):
Remark 15. The shape derivative of u is also defined as follows:
Domain and Boundary Transformations
Lemma 16 (see [18].)(1) Let φt ∈ L1(Ωt). Then φt∘Tt ∈ L1(Ω) and
(2) Let φt ∈ L1(∂Ωt). Then φt∘Tt ∈ L1(∂Ω) and
Proofs can be found in [13, 18].
Domain and Boundary Differentiation. We recall some results concerning the derivative of integrals with respect to the domain of integration. For the first theorem, it is sufficient to have C0,1 domains while the second theorem requires C1,1 domains. For proofs, see [18].
Theorem 17 (domain differentiation formula). Let u ∈ C(IV, W1,1(U)) and suppose exists in L1(U). Then
Theorem 18 (boundary differentiation formula). Let u be defined in a neighborhood of Γ. If u ∈ C(IV, W2,1(U)) and , then
The First-Order Eulerian Derivative
Definition 19. The Eulerian derivative of the shape functional J : Ω → ℝ defined in (7) at the domain Ω in the direction of the deformation field V ∈ Θ is given by
Remark 20. J is said to be shape differentiable at Ω if dJ(Ω; V) exists for all V ∈ Θ and is linear and continuous with respect to V.
4. Main Result
In this section we derive in a rigorous manner the first-order shape derivative of the Kohn-Vogelius functional J, defined by (7), subject to the Dirichlet and Neumann boundary value problems (BVPs) (4) and (6), respectively. Our strategy bypasses the material or shape derivatives of states. In the derivation, we have employed techniques used in [9, 10, 13] but there is no need to use adjoint variables.
This section discusses the variational forms of the PDEs, the state variables in the perturbed domains, the Hölder continuity of the state variables, and the higher regularity of the solutions to the BVPs. The rest of the proof is presented in the last part of this section.
4.1. Variational Forms of the Dirichlet and Neumann Problems
First, we determine the variational equations for the Dirichlet and the Neumann problems. The variational form of the Dirichlet problem (4) is given by the following.
4.2. Analysis of State Variables in Deformed Domains
Remark 21. The function ut : Ωt → ℝ can be referred to as the reference domain by composing ut with Tt; that is,
Next, we consider (68) whose variational form is formulated as follows.
4.3. Hölder Continuity of the States
We show that and are Hölder continuous on t.
Theorem 22 (see [13].)The solutions of (74) are uniformly bounded in H1(Ω) for t ∈ (−tV, tV) and
Proof. We first prove the uniform boundedness of in H1(Ω) for t ∈ (−tV, tV). Since , by using coercivity of At we get
Now we take the difference between the weak form of (4) and the variational equation (74), to get
If ∇yt = 0, then the inequality above holds. For ∇yt ≠ 0 we have
Theorem 23. The solutions of (84) are uniformly bounded in H1(Ω) for t ∈ (−tV, tV) and
Proof. Subtracting (65) from (84) for all we get
We now show that is bounded uniformly in t in L2(Ω). Since , we have
4.4. Higher Regularity of the Solutions
In this section we will show that the solutions to the PDEs (4) and (6) have higher regularity. We begin by considering the state variable uD, uN ∈ H1(Ω). For C1,1 domains, we show that these solutions also exist in H2(Ω) and more generally in Hk+2(Ω) if domains are of class Ck+1,1, k ≥ 0.
To prove higher regularity of uD, we require the following two theorems, which are proven in [22].
Theorem 24 (see [22], page 124.)Let Ω be a bounded open subset of ℝn with a C1,1 boundary. Consider the Dirichlet boundary value problem:
- (i)
ai = 0, 1 ≤ i ≤ n and a0 ≥ 0 a.e. or
- (ii)
a0 ≥ β > 0 a.e.
Theorem 25 (see [22], page 128.)Let Ω be a bounded open subset of ℝn with a Ck+1,1 boundary. Consider the operator A defined by (110) with , and assume that there exists α > 0 such that (112) holds for all ζ ∈ ℝn and for every . Also, consider a real boundary operator B which is either the identity operator (order d = 0) or with , 1 ≤ i ≤ n (order d = 1) and everywhere on Γ : = ∂Ω. Furthermore, assume that u ∈ W2,p(Ω) satisfies Au = f ∈ Wk,p(Ω) and γBu = g ∈ W2+k−d−1/p,p(Γ). Then u ∈ Wk+2,p(Ω).
We will also justify the higher regularity of uN. We use the following results whose proofs are given in the corresponding texts.
Theorem 26 (see [23], page 316.)Let Ω be a bounded open subset of ℝn. Suppose u ∈ H1(Ω) is a weak solution of the PDE
Theorem 27 (see [24], page 12.)Let Ω ⊂ ℝn be a bounded domain with Ck+1,1 boundary ∂Ω for some nonnegative integer k. Suppose the data f and g of the problem
For proof, see [22].
Theorem 28 (see [22], page 84.)Let Ω ⊂ ℝn be a bounded domain with C1,1 boundary Γ and 1 < p < ∞. Consider the Neumann problem
For proof, see [22].
Using the theorems presented above, we will now prove our claim that the solutions to the PDEs (4) and (6) have indeed higher regularity. This result is given in the following theorem.
Theorem 29. Let Ω be a bounded domain with boundary of class C1,1. Let uD, uN ∈ H1(Ω) be weak solutions of the BVPs (4) and (6), respectively. Then uD and uN also belong to H2(Ω). More generally, if Ω is of class Ck+1,1, where k is a nonnegative integer, then uD and uN are elements of Hk+2(Ω).
Proof. We first consider the solution uD ∈ H1(Ω) to the Dirichlet problem (4). We use Theorem 25 to show that uD is an element of H2(Ω). Here, (110) is applied with the following settings.
We consider n = 2. The domain Ω is of class C1,1. L = −Δ, and hence aij = aji = −1 for i = j and aij = aji = 0 for i ≠ j, with i, j = 1,2. We also observe that , for all ζ = (ζ1, ζ2) T. Thus α = 1. Furthermore, we have the following data: f = 0 ∈ L2(Ω), g = 1 ∈ H3/2(Γ), g = 0 ∈ H3/2(Σ). Therefore, by using Theorem 24, there exists a unique u = uD ∈ H2(Ω), which is a solution to (4).
For higher regularity of uD we apply Theorem 25. At first we consider C2,1-domains. In this case, k = 1. We have aij = aji = −1 for i = j and aij = aji = 0 for i ≠ j, i, j = 1,2. The operator B is the identity operator, thus of order d = 0. From the first consequence, it is known that u ∈ H2(Ω) satisfies −Δu = 0 and u = g on ∂Ω, where g = 1 ∈ H5/2(Γ), g = 0 ∈ H5/2(Σ). Therefore, by applying Theorem 25, we have u = uD ∈ H3(Ω). In general, for smoother domains with Ck+1,1 boundaries, solutions to (4) are elements of Hk+2.
Next, we recall that, for C1,1 domain, there is a weak solution uN ∈ H1(Ω) to the boundary value problem (6). We also show that the solution actually lies in H2(Ω) and if the domain is more regular, then so is the solution. More precisely, we want to show that if Ω is a domain whose boundary is of class Ck+1,1, then uN is in Hk+2(Ω), where k is a nonnegative integer. For this purpose we need Theorem 26 which implies uN ∈ C∞(Ω).
Choose a bounded connected domain G with C∞ boundary Γ1 such that and , where A and B are the domains described in Section 2. Let Ω1 be the annulus having boundaries Γ and Γ1, and let Ω2 be the other annulus with boundaries Γ1 and Σ. First, we consider the following elliptic problem on Ω1:
Second, we consider the following boundary value problem:
Hence, for Ck+1,1-domains , if we combine and , we get uN ∈ Hk+2(Ω1 ∪ Ω2). Moreover, uN is C∞ in a neighborhood of Γ1 because uN ∈ C∞(Ω). Therefore, uN ∈ Hk+2(Ω).
Remark 30. In the computation of the first-order shape derivative, since we are dealing with C1,1-domains, we may consider H2-regularity for the solutions uD and uN, as justified by Theorem 29.
4.5. The Shape Derivative of J
First, we state and prove the following lemma.
Lemma 31. Let Ω ⊂ ℝn be a bounded Lipschitz domain. Then the following equation:
- (i)
F ∈ H1(Ω; ℝn) and g ∈ H1(Ω);
- (ii)
and g ∈ W1,1(Ω).
Proof. First we recall the Gauss’ divergence theorem in ℝn saying that if a domain Ω ⊂ ℝn is a bounded Lipschitz domain, then we have
(i) If F ∈ H1(Ω; ℝn) and g ∈ H1(Ω), then (div F)g ∈ L1(Ω), F · ∇g ∈ L1(Ω), and the integral ∫∂Ω g(F · n) is bounded. Hence, (119) is well defined. Note that the formula
(ii) If and g ∈ W1,1(Ω), then (div F)g ∈ L1(Ω) and F · ∇g ∈ L1(Ω). Note that γg ∈ L1(∂Ω) (cf. [25, page 316]), where γg refers to the trace of g on ∂Ω, hence g(F · n) ∈ L1(∂Ω). Therefore, (119) is also well defined for this case. Using similar arguments as above and using the density of in W1,1(Ω) we can show that (119) is also valid for this case.
Now we apply Lemma 31 to prove the next lemma.
Lemma 32 (see [1].)Let uD and uN belonging to H2(Ω) satisfy the Dirichlet problem (4) and the Neumann problem (6), respectively. Then
Proof. From Lemma 11, we recall the expression for A, which is given by A = (div V)I − ((DV)+(DV) T). Our first goal is to derive an expression for ∫Ω A∇u · ∇v for u, v ∈ H2(Ω). We begin by writing ∫Ω A∇u · ∇v as follows:
Integrating both sides of (132) over Ω, applying Stoke’s theorem, and considering V = 0 on Γ we end up with
On the other hand, by replacing both u and v by uN and by considering that −ΔuN = 0 in Ω and ∂uN/∂n = λ on Σ, we derive (126) as
Now, we derive the explicit form of the first-order shape derivative of J.
Theorem 33. For C1,1 bounded domain Ω, the first-order shape derivative of the Kohn-Vogelius cost functional
Proof. First we consider the functionals defined on the reference domain and perturbed domains
We know from the previous section that uD and uN exist in H2(Ω) since Ω is of class C1,1. Using this smoothness we can now apply Lemma 32 and write (156) as follows:
5. Conclusion
In this paper we derived the explicit form of the first-order Eulerian shape derivative of the Kohn-Vogelius cost functional given by (7) in a rigorous manner. As seen in the presentation, we can avoid working on the shape derivatives of the states and apply their Hölder continuity instead. We employed techniques similar to [9, 13] but it was not necessary to introduce adjoint variables. For the shape derivative of the cost functional to be well defined we observe that we can consider domains with C1,1 boundaries and we need H2 regularity for the state variables.
Theorem 34 (see [26], page 318.)Let Ω be a domain with Ck+1 boundary Γ for some integer k ≥ 0. Assuming that at Ω a shape gradient of J(Ω) exists. Then there exists a scalar distribution g in 𝒟k(Γ)′ such that
Proof. See [26].
Acknowledgments
The paper is partially supported by the ÖAD—Austrian Agency for International Cooperation in Education and Research for the Technologiestipendien Südostasien (Doktorat) scholarship in the frame of the ASEA-Uninet; the SFB Research Center ‘‘Mathematical Optimization and Applications in Biomedical Sciences” SFB F32; the University of the Philippines Baguio. The first author is thankful to the Institute for Mathematics and Scientific Computing, University of Graz, for funding a presentation of partial results during the 7th European Conference on Elliptic and Parabolic Problems held on May 21–25, 2012 at Gaeta, Italy. He is likewise grateful to Professor Gilbert Peralta for his helpful insights and suggestions. Moreover, he is thanking UP Baguio for giving a Ph.D. incentive grant for writing this paper. Last but not least, the authors would like to thank the referees for devoting time to review this material.




