A theoretical study is carried out to obtain an analytic solution of heat and mass transfer in a vertical porous channel with rotation and Hall current. A constant suction and injection is applied to the two insulating porous plates. A strong magnetic field is applied in the transverse direction. The entire system rotates with uniform angular velocity Ω about the axis normal to the plates. The governing equations are solved by perturbation technique to obtain the analytical results for velocity, temperature, and concentration fields and shear stresses. The steady and unsteady resultant velocities along with the phase differences for various values of physical parameters are discussed in detail. The effects of rotation, buoyancy force, magnetic field, thermal radiation, and heat generation parameters on resultant velocity, temperature, and concentration fields are analyzed.

1. Introduction

Free convection in channel flow has many important applications in designing ventilating and heating of buildings, cooling of electronic components of a nuclear reactor, bed thermal storage, and heat sink in the turbine blades. Convective flows driven by temperature difference of the bounding walls of channels are important in industrial applications. El-Hakiem [1] studied the unsteady MHD oscillatory flow on free convection radiation through a porous medium with a vertical infinite surface that absorbs the fluid with a constant velocity. Jaiswal and Soundalgekar [2] analyzed the effects of suction with oscillating temperature on a flow past an infinite porous plate. Singh et al. [3] studied the unsteady free convective flow in a porous medium bounded by an infinite vertical porous plate in the presence of rotation. Pal and Shivakumara [4] studied the mixed convection heat transfer from a vertical plate in a porous medium.

Hydromagnetic convection with heat transfer in a rotating medium has important applications in MHD generators and accelerators design, geophysics, and nuclear power reactors. MHD free convection and mass transfer flows in a rotating system have diverse applications. The effects of Hall currents cannot be neglected as the conducting fluid when it is an ionized gas, and applied field strength is strong then the electron cyclotron frequency ω = eB/m (where e, B, and m denote the electron charge, the applied magnetic field, and mass of an electron, resp.) exceeds the collision frequency so that the electron makes cyclotron orbit between the collisions which will divert in a direction perpendicular to the magnetic and electric fields directions. Thus, if an electric field is applied perpendicular to the magnetic field then whole current will not pass along the electric field. This phenomena of flow of the electric current across an electric field with magnetic field is known as Hall effect, and accordingly this current is known as Hall current [5]. Thus, it is essential to analyze the effects of Hall currents in many industrial problems. Gupta [6] has studied the influence of Hall current on steady MHD flow in a viscous fluid. Jana et al. [7] analyzed the hall effect in steady flow past an infinite porous flat plate. Makinde and Mhone [8] studied hydromagnetic oscillatory flow through a channel having porous medium. Zhang and Wang [9] analyzed the effect of magnetic field in a power-law fluid over a vertical stretching sheet. Hameed and Nadeem [10] analyzed unsteady hydromagnetic flow of a non-Newtonian fluid over a porous plate. Makinde et al. [11] examined the effect of magnetic field in a rotating porous medium cylindrical annulus. Sibanda and Makinde [12] analyzed effects of magnetic fields on heat transfer on a rotating disk in a porous medium with Ohmic heating and viscous dissipation. Pop and Watanabe [13] analyzed convective flow of a conducting fluid in the presence of magnetic field and Hall current. Saha et al. [14] studied Hall current effect on MHD natural convection flow from vertical flat plate. Recently, Pal et al. [15] examined the influence of Hall current and chemical reaction on oscillatory mixed convection radiation of a micropolar fluid in a rotating system.

Radiation effects on free convection flow have become very important due to its applications in space technology, processes having high temperature, and design of pertinent equipments. Moreover, heat and mass transfer with thermal radiation on convective flows is very important due its significant role in the surface heat transfer. Recent developments in gas cooled nuclear reactors, nuclear power plants, gas turbines, space vehicles, and hypersonic flights have attracted research in this field. The unsteady convective flow in a moving plate with thermal radiation were examined by Cogley et al. [16] and Mansour [17]. The combined effects of radiation and buoyancy force past a vertical plate were analyzed by Hossain and Takhar [18]. Hossain et al. [19] analyzed the influence of thermal radiation on convective flows over a porous vertical plate. Seddeek [20] explained the importance of thermal radiation and variable viscosity on unsteady forced convection with an align magnetic field. Muthucumaraswamy and Senthil [21] studied the effects of thermal radiation on heat and mass transfer over a moving vertical plate. Pal [22] investigated convective heat and mass transfer in a stagnation-point flow towards a stretching sheet with thermal radiation. Aydin and Kaya [23] justified the effects of thermal radiation on mixed convection flow over a permeable vertical plate with magnetic field. Mohamed [24] studied unsteady MHD flow over a vertical moving porous plate with heat generation and Soret effect. Chauhan and Rastogi [25] analyzed the effects of thermal radiation, porosity, and suction on unsteady convective hydromagnetic vertical rotating channel. Ibrahim and Makinde [26] investigated radiation effect on chemically reaction MHD boundary layer flow of heat and mass transfer past a porous vertical flat plate. Pal and Mondal [27] studied the effects of thermal radiation on MHD Darcy-Forchheimer convective flow past a stretching sheet in a porous medium. Palani and Kim [28] analyzed the effect of thermal radiation on convection flow past a vertical cone with surface heat flux. Recently, Mahmoud and Waheed [29] examined thermal radiation on flow over an infinite flat plate with slip velocity.

The study of heat and mass transfer due to chemical reaction is also very importance because of its occurrence in most of the branches of science and technology. The processes involving mass transfer effects are important in chemical processing equipments which are designed to draw high value products from cheaper raw materials with the involvement of chemical reaction. In many industrial processes, the species undergo some kind of chemical reaction with the ambient fluid which may affect the flow behaviour and the production quality of final products. Aboeldahab and Elbarbary [30] examined heat and mass transfer over a vertical plate in the presence of magnetic field and Hall effect. Abo-Eldahab and El Aziz [31] investigated the Hall current and Joule heating effects on electrically conducting fluid past a semi-infinite plate with strong magnetic field and heat generation/absorption. Kandasamy et al. [32] discussed the effects of chemical reaction and magnetic field on heat and mass transfer over a vertical stretching surface. Muthucumaraswamy and Janakiraman [33] analyzed the effects of mass transfer over a vertical oscillating plate with chemical reaction. Sharma and Singh [34] have analyzed the unsteady MHD free convection flow and heat transfer over a vertical porous plate in the presence of internal heat generation and variable suction. Sudheer Babu and Satya Narayan [35] examined chemical reaction and thermal radiation effects on MHD convective flow in a porous medium in the presence of suction. Makinde and Chinyoka [36] studied the effects of magnetic field on MHD Couette flow of a third-grade fluid with chemical reaction. Recently, Pal and Talukdar [37] investigated the influence of chemical reaction and Joule heating on unsteady convective viscous dissipating fluid over a vertical plate in porous media with thermal radiation and magnetic field.

The objective of the present study is to analyze the effects of Hall current, thermal radiation, and first-order chemical reaction on the oscillatory convective flow and mass transfer with suction injection in a rotating vertical porous channel. The present results are compared with those of Singh and Kumar [38], and a very good agreement is found.

2. Problem Formulation

We consider unidirectional oscillatory free convective flow of a viscous incompressible and electrically conducting fluid between two insulating infinite vertical permeable plates separated by a distance d. A constant injection velocity w₀ is applied at the stationary plate z^* = 0. Also, a constant suction velocity w₀ is applied at the plate z^* = d, which oscillates in its own plane with a velocity U^*(t^*) about a nonzero constant mean velocity U₀. The channel rotates as a rigid body with angular velocity Ω^* about the z^*-axis perpendicular to the planes of the plates. A strong transverse magnetic field of uniform strength H₀ is applied along the axis of rotation by neglecting induced electric and magnetic fields. The fluid is assumed to be a gray, emitting, and absorbing, but nonscattering medium. The radiative heat flux term can be simplified by using the Rosseland approximation. It is also assumed that the chemically reactive species undergo first-order irreversible chemical reaction.

The solenoidal relation for the magnetic field

, where

gives

(constant) everywhere in the flow field, which gives

. If

are the component of electric current density

, then the equation of conservation of electric charge

gives

. This constant is zero, that is,

everywhere in the flow since the plate is electrically non-conducting. The generalized Ohm’s law, in the absence of the electric field [39], is of the form

()

where

, σ, μ_e, ω_e, τ_e, e, n_e, and p_e are the velocity, the electrical conductivity, the magnetic permeability, the cyclotron frequency, the electron collision time, the electric charge, the number density of the electron, and the electron pressure, respectively. Under the usual assumption, the electron pressure (for a weakly ionized gas), the thermoelectric pressure, and ion slip are negligible, so we have from the Ohm’s law

()

from which we obtain that

()

Since the plates are infinite in extent, all the physical quantities except the pressure depend only on z^* and t^*. The physical configuration of the problem is shown in Figure 1. A Cartesian coordinate system is assumed, and z^*-axis is taken normal to the plates, while x^*- and y^*-axes are in the upward and perpendicular directions on the plate z^* = 0 (origin), respectively. The velocity components u^*, v^*, w^* are in the x^*-, y^*-, z^*-directions, respectively. The governing equations in the rotating system in presence of Hall current, thermal radiation, and chemical reaction are given by the following equations:

()

where m( = ω_eτ_e) is the Hall parameter, β and β^* are the coefficients of thermal and solutal expansion, c_p is the specific heat at constant pressure, ρ is the density of the fluid, ν is the kinematics viscosity, κ is the fluid thermal conductivity, g₀ is the acceleration of gravity, Q₀ is the additional heat source,

is the radiative heat flux, D_m is the molecular diffusivity, k₁ is the chemical reaction rate constant. The radiative heat flux is given by

, in which σ^* and k^* are the Stefan-Boltzmann constant and the mean absorption coefficient, respectively.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Physical configuration of the problem.

The initial and boundary conditions as suggested by the physics of the problem are

()

where ϵ is a small constant.

We now introduce the dimensionless variables as follows:

()

After combining (5) and (6) and taking q = u + iv, then (5)–(8) reduce to

()

where

is the modified thermal Grashof number,

is the modified solutal Grashof number, Pr = νρc_p/κ is the Prandtl number,

is the Hartmann number, Q_H = Q₀d²/κ is the heat source parameter, R = κk^*/4σ^*T_d is the radiation parameter, Sc = ν/Dm is the Schmidt number, and ξ = k₁d²/ν is the reaction parameter.

The boundary conditions (9) can be expressed in complex form as

()

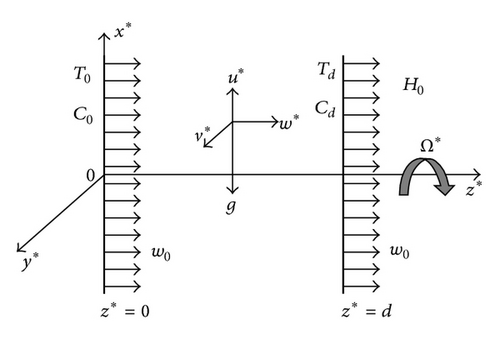
3. Method of Solution

The set of partial differential equations (11) cannot be solved in closed form. So it is solved analytically after these equations are reduced to a set of ordinary differential equations in dimensionless form. We assume that

()

where ℜ stands for q or θ or ϕ, and ϵ ≪ 1 which is a perturbation parameter. The method of solution is applicable for small perturbation.

Substituting (13) into (11) and comparing the harmonic and nonharmonic terms, we obtain the following ordinary differential equations:

()

where S = (M²(1 + im)/(1 + m²)) + 2iΩ and dashes denote the derivatives w.r.t. η.

The transformed boundary conditions are

()

The solutions of (14) under the boundary conditions (15) are

()

4. Amplitude and Phase Difference due to Steady and Unsteady Flow

Equation (16) corresponds to the steady part, which gives u₀ as the primary and v₀ as secondary velocity components. The amplitude (resultant velocity) and phase difference due to these primary and secondary velocities for the steady flow are given by

()

where u₀(η) + iv₀(η) = q₀(η).

Equations (17) and (18) together give the unsteady part of the flow. Thus, unsteady primary and secondary velocity components u₁(η) and v₁(η), respectively, for the fluctuating flow can be obtained from the following:

()

The amplitude (resultant velocity) and the phase difference of the unsteady flow are given by

()

where u₁(η) + iv₁(η) = q₁(η)e^it + q₂(η)e^−it.

The amplitude (resultant velocity) and the phase difference

()

where u = Real part of q and v = Imaginary part of q.

5. Amplitude and Phase Difference of Shear Stresses due to Steady and Unsteady Flow at the Plate

The amplitude and phase difference of shear stresses at the stationary plate (η = 0) for the steady flow can be obtained as

()

where

()

For the unsteady part of flow, the amplitude and phase difference of shear stresses at the stationary plate (η = 0) can be obtained as

()

where

()

The amplitude and phase difference of shear stresses at the stationary plate (η = 0) for the flow can be obtained as

()

where τ_x = Real part of (∂q/∂η)_η=0 and τ_y = Imaginary part of (∂q/∂η)_η=0.

The Nusselt number

()

The rate of heat transfer (i.e., heat flux) at the plate in terms of amplitude and phase is given by

()

The Sherwood number

()

The rate of mass transfer (i.e., mass flux) at the plate in terms of amplitude and phase is given by

()

6. Results and Discussion

The system of ordinary differential equations (14) with boundary conditions (15) is solved analytically by employing the perturbation technique. The solutions are obtained for the steady and unsteady velocity fields from (16)–(18), temperature fields from (19)–(21), and concentration fields are given by (22)–(24). The effects of various parameters on the thermal, mass, and hydrodynamic behaviors of buoyancy-induced flow in a rotating vertical channel are studied. The results are presented graphically and in tabular form. Temperature of the heated wall (left wall) at z^* = 0 is a function of time as given in the boundary conditions, and the cooled wall at z^* = d is maintained at a constant temperature. Further, it is assumed that the temperature difference is small enough so that the density changes of the fluid in the system will be small. When the injection/suction parameter λ is positive, fluid is injected through the hot wall into the channel and sucked out through the cold wall. The numerical results of the amplitude of the shear stresses and the phase difference of the shear stresses at the stationary plate (z^* = 0) for the steady and unsteady flow are presented in Table 1. The effect of various physical parameters on flow, heat, concentration fields, skin-friction, Nusselt number, and Sherwood number are presented graphically in Figures 2–16.

Table 1. Comparison results for the resultant velocity or amplitude and the phase difference of the unsteady flow with Singh and Kumar [38] for different values of Gr, M, m, λ, Ω, Pr, and Gm = 0.0, R = ∞, ξ = 0.0, Sc → 0.0 (in present problem).

Gr	M	m	λ	Ω	Pr	Singh and Kumar [38]		Present results
Gr	M	m	λ	Ω	Pr	τ_0r	β₀	τ_0r	β₀
5	2	1	0.5	10	0.71	4.5847	0.7279	4.5847	0.7279
10	2	1	0.5	10	0.71	4.6515	0.6815	4.6515	0.6815
5	4	1	0.5	10	0.71	5.2797	0.6395	5.2797	0.6395
5	2	3	0.5	10	0.71	4.4862	0.7627	4.4862	0.7627
5	2	1	1.0	10	0.71	4.6162	0.6229	4.6162	0.6229
5	2	1	0.5	20	0.71	6.3323	0.7614	6.3323	0.7614
5	2	1	0.5	40	0.71	8.8924	0.7783	8.8924	0.7783
5	2	1	0.5	80	0.71	12.558	0.7857	12.558	0.7857
5	2	1	0.5	10	7.0	4.5726	0.7198	4.5726	0.7198

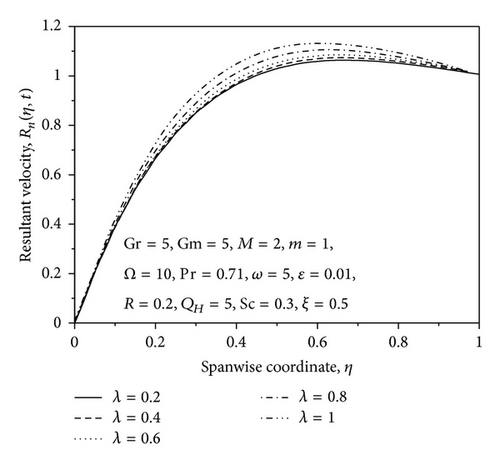
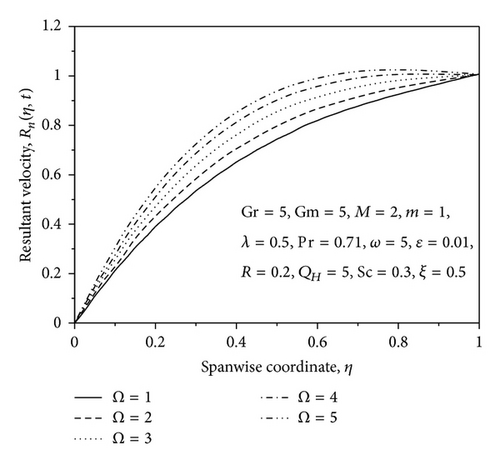
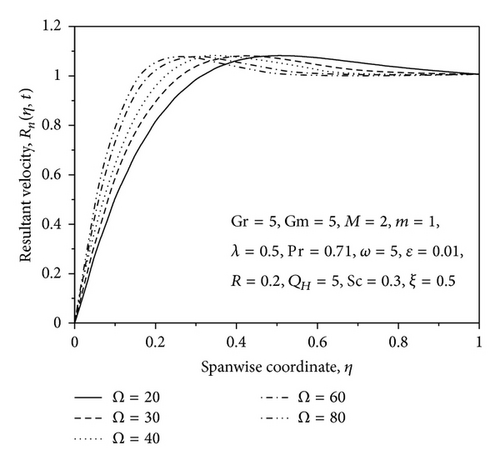
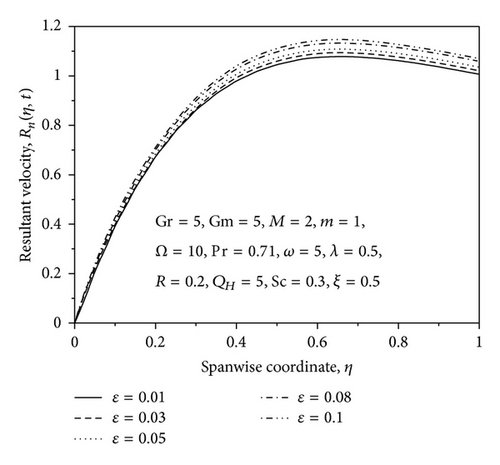
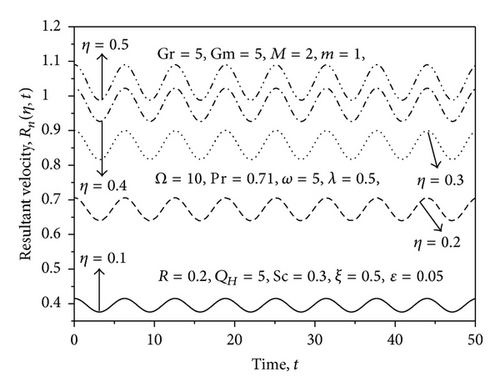
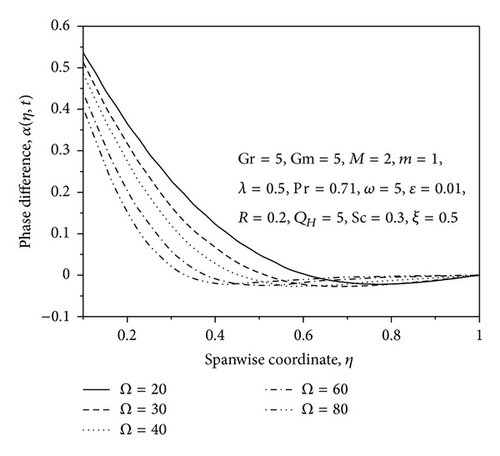
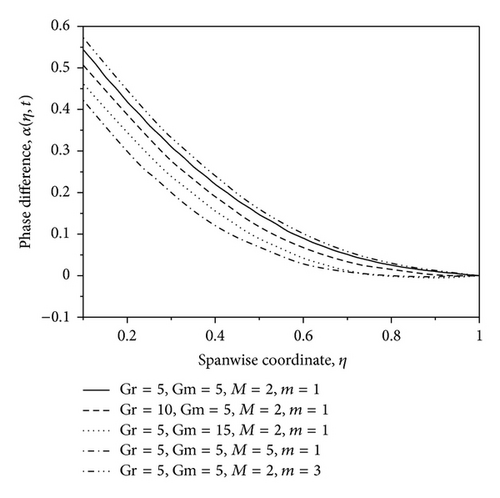
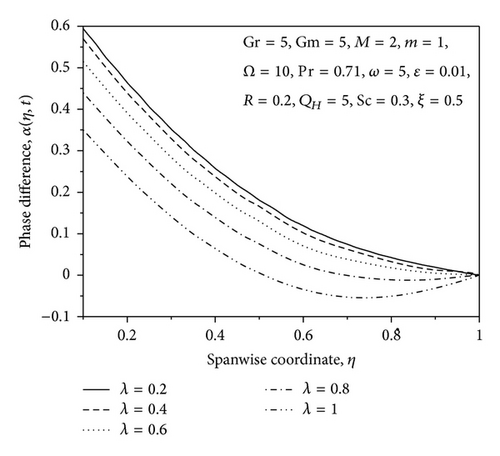
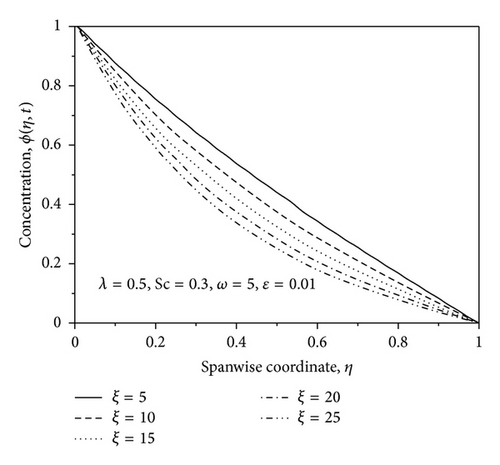
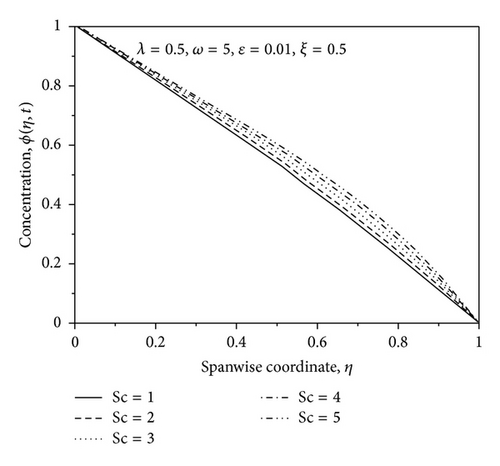
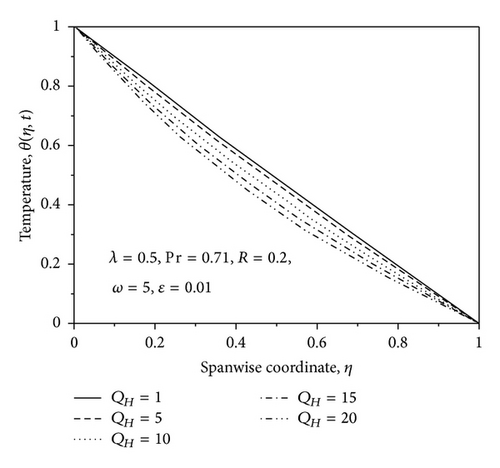
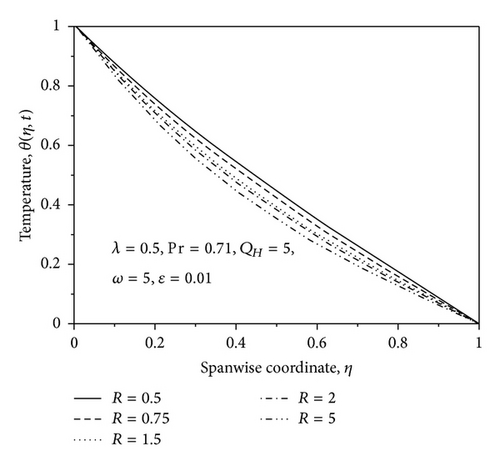
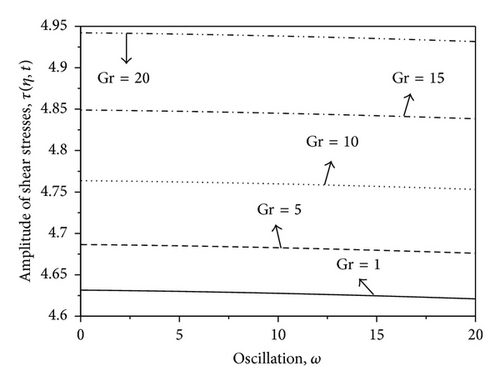
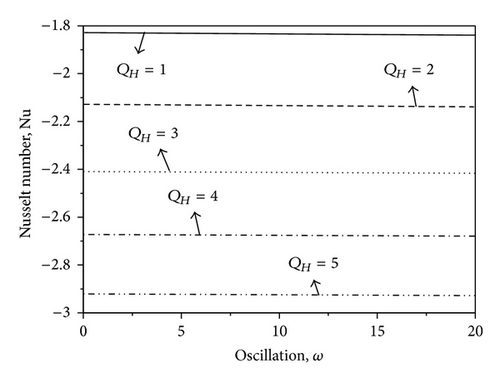
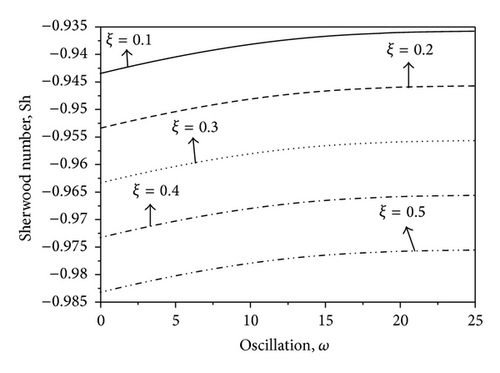
Table 1 shows a comparative study of the present results of amplitude and phase difference of shear stresses for the steady flow with those of Singh and Kumar [38]. It is seen from this table that the present results coincide very well with those of Singh and Kumar [38]. This confirms that the present analytical solutions are correct and accurate. Further, it is observed from this table that the effects of increasing the value of thermal Grashof number Gr, magnetic field M, and injection/suction parameter λ are to increase amplitude and decrease the phase difference of shear stresses for the steady flow, whereas reverse effect is found by increasing the Hall parameter, m. The effects of increasing the angular velocity Ω are to increase both amplitude and phase difference of shear stresses, whereas reverse effects are seen by increasing the values of the Prandtl number. The computed results τ_0r, τ_1r, β₀, β₁ for the present problem are provided in Table 2 for various values of Gm, R, Q_H, Sc, ξ, and m. It is seen from this table that the values of τ_0r and τ_1r increase whereas the values of β₀ and β₁ decrease with the increase of solutal Grashof number Gm, but the effects are reversed with an increase in the Hall parameter m, that is, the value of β₀ and β₁ are increased whereas there is decrease in the values of τ_0r and τ_1r. Also, it is found that the values of τ_0r, β₀β₁ increase with an increase in the radiation parameter R. It is noted that the values of both τ_0r and β₀ increase due to an increase in the heat source parameter Q_H and chemical reaction parameter ξ, whereas the effects are reversed with the increase in the Schmidt number, that is, the values of τ_0r, τ_1rβ₁ decrease with an increase in the Schmidt number. Also, it is found that the value of β₁ decreases with an increase in the heat source parameter Q_H, chemical reaction parameter ξ and Schmidt number Sc.

Table 2. Values of τ_0r, β₀, τ_1r, and β₁ for the reference values of Gr = 5.0, M = 2.0, λ = 0.5, Ω = 10.0, Pr = 0.71, and ω = 5.0 at t = π/4.

Gm	R	Q_H	Sc	ξ	m	τ_0r	β₀	τ_1r	β₁
5.0	1.0	5.0	0.15	0.1	1.0	4.6540	0.6877	6.4123	0.7980
10.0	1.0	5.0	0.15	0.1	1.0	4.7299	0.6437	6.4542	0.7485
5.0	5.0	5.0	0.15	0.1	1.0	4.6543	0.6900	6.4094	0.8011
5.0	1.0	10.0	0.15	0.1	1.0	4.6545	0.6908	6.4219	0.8010
5.0	1.0	5.0	0.60	0.1	1.0	4.6534	0.6869	6.3805	0.8006
5.0	1.0	5.0	0.15	1.0	1.0	4.6541	0.6880	6.4132	0.7983
5.0	1.0	5.0	0.15	1.0	3.0	4.5464	0.7197	6.3064	0.8366

The profiles for resultant velocity R_n for the flow are shown in Figures 2–6 for suction/injection parameter λ and for small and large values of rotation parameter Ω, ϵ, and η, respectively. From Figure 2, it is observed that the increase in the suction parameter λ leads to an increase of R_n within the stationary plates. Similar trend of R_n profiles is seen by increasing the rotation parameter Ω, that is, resultant velocity profiles increase with increase in the rotation parameter Ω (small values) as shown in Figure 3. However, the opposite effect occurs near the right wall for large values of Ω as shown in Figure 4. This effect is due to the rotation effects being more dominant near the walls, so when Ω reaches high values, the secondary velocity component v decreases with increase in Ω while approaching to the right plate. From Figure 5, it is observed that the increase in the ϵ leads to an increase of R_n within the stationary plates. From Figure 6, it is seen that the resultant velocity profiles increases with increase in η; also it is observed that the velocity oscillates with increasing time. The phase difference α for the flow is shown graphically in Figure 7 for various values of rotation parameter Ω. From this figure, it is observed that the phase angle α decreases with an increase in rotation parameter. Figure 8 shows the variation of α against η for different values of thermal Grashof number Gr, solutal Grashof number Gm, Hartmann number M, and Hall parameter m. From this figure it is found that the values of α decrease with an increase in the value of Gr, Gm and M, whereas reverse trend is seen on the values of α by increasing the value of the Hall parameter m. The phase difference α for the flow is shown graphically in Figure 9 for various positive values of suction/injection parameter λ. The figure shows that the phase angle α decreases with the increase of suction parameter.

The effect of reaction rate parameter ξ on the species concentration profiles for generative chemical reaction is shown in Figure 10. It is noticed for the graph that there is a marked effect of increasing the value of the chemical reaction rate parameter ξ on concentration distribution ϕ in the boundary layer. It is observed that increasing the value of the chemical reaction parameter ξ decreases the concentration of species in the boundary layer; this is due to the fact that destructive chemical reduces the solutal boundary layer thickness and increases the mass transfer. Opposite trend is seen in the case when Schmidt number is increased as noted in Figure 11. It may also be observed from this figure that the effect of Schmidt number Sc is to increase the concentration distribution in the solutal boundary layer.

Figure 12 has been plotted to depict the variation of temperature profiles against η for different values of heat absorption parameter Q_H by fixing other physical parameters. From this graph, we observe that temperature θ decreases with increase in the heat absorption parameter Q_H because when heat is absorbed, the buoyancy force decreases the temperature profile. Figure 13 represents graph of temperature distribution with η for different values of radiation parameter. From this figure, we note that the initial temperature θ = 1.0 decreases to zero satisfying the boundary condition at η = 1.0. Further, it is observed from this figure that increase in the radiation parameter decreases the temperature distribution in the thermal boundary layer due to decrease in the thickness of the thermal boundary layer with thermal radiation parameter R. This is because large values of radiation parameter correspond to an increase in dominance of conduction over radiation, thereby decreasing the buoyancy force and the temperature in the thermal boundary layer.

Figures 14–16 show the amplitude of skin-friction, Nusselt number, and Sherwood number against frequency parameter ω for different values of Gr, Q_H and ξ, respectively. From Figure 14, it is observed that the skin friction increases with increasing the values of Gr. Also, the skin friction decreases slowly with increasing the value of ω. The amplitude of Nusselt number decreases with increasing the value of heat source parameter Q_H which is shown in Figure 15. Figure 16 shows the variation of Sherwood number with ξ and ω. From this figure, it is seen that the Sherwood number decreases with increasing the values of chemical reaction parameter ξ, and the opposite trend is seen with increasing the values of ω.

7. Conclusions

The influence of hall current and chemical reaction on unsteady MHD heat and mass transfer of an oscillatory convective flow in a rotating vertical porous channel with thermal radiation and injection is studied analytically. Computed results are presented to exhibit their dependence on the important physical parameters. We conclude the following from the numerical results.

(i)
An increase in Q_H leads to an increase in τ_0r, β₀, τ_1r and decrease in β₁.
(ii)
An increase in radiation parameter R and chemical reaction parameter ξ leads to increase in τ_0r, β₀, and β₁ but decrease in τ_1r.
(iii)
An increase in Gr, Gm, M, Ω, and λ leads to decrease in α₀ and α₁, whereas reverse effect is seen by increasing Hall parameter m.
(iv)
The amplitude R_n increases with the increase of λ and Ω.
(v)
The value of R_n decreases with the increase in chemical reaction parameter ξ and oscillation parameter ω.
(vi)
The skin friction increases with increase in thermal Grashof number Gr.

Nomenclature

C^*:: Dimensional concentration
C₀:: Concentration at the left plate
C_d:: Concentration at the right plate
c_p:: Specific heat at constant pressure
d:: Distance of the plates
D_m:: Chemical molecular diffusivity
e:: Electric charge
g₀:: Acceleration due to gravity
Gm:: Modified Grashof number for mass transfer
Gr:: Modified Grashof number for heat transfer
:: Magnetic field
H₀:: Magnetic field of uniform strength
H_x:: x-component of magnetic field
:: Current density
J_x:: x-component of current density
k^*:: Mean absorption coefficient
k₁:: Chemical reaction rate constant
m:: Hall parameter
M:: Hartmann number
Nu:: Nusselt number
n_e:: Number density of the electron
P^*:: Dimensional pressure
p_e:: Electron pressure
Pr:: Prandtl number
:: Radiative heat flux
Q₀:: Dimensional heat source
Q_H:: Heat source parameter
R:: Radiation parameter
R₀:: Amplitude for steady flow
R_n:: Resultant velocity
R_v:: Amplitude for unsteady flow
Sc:: Schmidt number
Sh:: Sherwood number
t^*:: Dimensional time
T^*:: Dimensional temperature
T₀:: Temperature at the left wall
T_d:: Temperature at the right wall
U₀:: Nonzero constant mean velocity
u₀:: Primary velocity component for steady flow
u₁:: Primary velocity component for unsteady flow
:: Electron velocity
v₀:: Secondary velocity component for steady flow
v₁:: Secondary velocity component for unsteady flow
u^*, v^*, w^*:: Velocity components are in the x^*-, y^*-, z^*-directions, respectively
w₀:: Dimensional injection/suction velocity.

Greek Symbols

α₀:: Phase difference for steady flow
α₁:: Phase difference for unsteady flow
α:: Phase difference of the flow
β:: Coefficient of thermal expansion
β^*:: Coefficient of solutal expansion
β₀:: Phase difference of shear stresses for the steady flow
β₁:: Phase difference of shear stresses for the unsteady flow
β₂:: Phase difference of shear stresses for the flow
δ:: Phase difference of mass flux
ϵ:: Small positive constant
η:: Dimensionless distance
γ:: Phase difference of heat flux
κ:: Fluid thermal conductivity
λ:: Injection/suction parameter
μ:: Dynamic viscosity
μ_e:: Magnetic permeability
ν:: Kinematic viscosity
ω:: Oscillation parameter
Ω^*:: Dimensional angular velocity
Ω:: Angular velocity
ω_e:: Cyclotron frequency
Φ:: Amplitude of mass flux
ϕ:: Nondimensional concentration
ρ:: Density
σ:: Electric conductivity
σ^*:: Stefan-Boltzmann constant
τ:: Amplitude of shear stresses for the flow
τ_0r:: Amplitude of shear stresses for the steady flow
τ_1r:: Amplitude of shear stresses for the unsteady flow
τ_e:: Electron collision time
θ:: Non-dimensional temperature
Θ:: Amplitude of heat flux.

Acknowledgment

One of the authors (Dulal Pal) is grateful to the University Grants Commission (UGC), New Delhi, for providing financial support under SAP-DRS (Phase-II) Grant.

Appendix

Consider the following:

()

References

1 El-Hakiem M. A., MHD oscillatory flow on free convection-radiation through a porous medium with constant suction velocity, Journal of Magnetism and Magnetic Materials. (2000) 220, no. 2-3, 271–276, 2-s2.0-0034298485, https://doi.org/10.1016/S0304-8853(00)00444-3.
Google Scholar
2 Jaiswal B. S. and Soundalgekar V. M., Oscillating plate temperature effects on a flow past an infinite vertical porous plate with constant suction and embedded in a porous medium, Heat and Mass Transfer. (2001) 37, no. 2-3, 125–131, 2-s2.0-0035303292, https://doi.org/10.1007/s002310000180.
Google Scholar
3 Singh K. D., Gorla M. G., and Raj H., A periodic solution of oscillatory couette flow through porous medium in rotating system, Indian Journal of Pure and Applied Mathematics. (2005) 36, no. 3, 151–159, 2-s2.0-24944457624.
Google Scholar
4 Pal D. and Shivakumara I. S., Mixed convection heat transfer from a vertical heated plate embedded in a sparsely packed porous medium, International Journal of Applied Mechanics and Engineering. (2006) 11, no. 4, 929–939.
Google Scholar
5 Cowling T. G., Magnetohydrodynamics, 1957, Interscience Publishers, New York, NY, USA.
Google Scholar
6 Gupta A. S., Hydromagnetic flow past a porous flat plate with hall effects, Acta Mechanica. (1975) 22, no. 3-4, 281–287, 2-s2.0-0016627115, https://doi.org/10.1007/BF01170681.
Google Scholar
7 Jana R. N., Gupta A. S., and Datta N., Hall effects on the hydro magnetic flow past an infinite porous flat plate, Journal of the Physical Society of Japan. (1977) 43, no. 5, 1767–1772, 2-s2.0-0017551357.
Google Scholar
8 Makinde O. D. and Mhone P. Y., Heat transfer to MHD oscillatory flow in a channel filled with porous medium, Romanian Journal of Physics. (2005) 50, 931–938.
Google Scholar
9 Zhang Z. and Wang J., On the similarity solutions of magnetohydrodynamic flows of power-law fluids over a stretching sheet, Journal of Mathematical Analysis and Applications. (2007) 330, no. 1, 207–220, 2-s2.0-33846914472, https://doi.org/10.1016/j.jmaa.2006.07.059.
Web of Science® Google Scholar
10 Hameed M. and Nadeem S., Unsteady MHD flow of a non-Newtonian fluid on a porous plate, Journal of Mathematical Analysis and Applications. (2007) 325, no. 1, 724–733, 2-s2.0-33750311232, https://doi.org/10.1016/j.jmaa.2006.02.002.
Google Scholar
11 Makinde O. D., Beg O. A., and Takhar H. S., Magnetohydrodynamic viscous flow in a rotating porous medium cylindrical annalus with on applied radial magnetic field, International Journal of Applied Mathematics and Mechanics. (2009) 5, 68–81.
Google Scholar
12 Sibanda P. and Makinde O. D., On steady MHD flow and heat transfer past a rotating disk in a porous medium with ohmic heating and viscous dissipation, International Journal of Numerical Methods for Heat and Fluid Flow. (2010) 20, no. 3, 269–285, 2-s2.0-77951231539, https://doi.org/10.1108/09615531011024039.
Google Scholar
13 Pop I. and Watanabe T., Hall effects on magnetohydrodynamic free convection about a semi-infinite vertical flat plate, International Journal of Engineering Science. (1994) 32, no. 12, 1903–1911, 2-s2.0-0028671621.
Google Scholar
14 Saha L. K., Siddiqa S., and Hossain M. A., Effect of Hall current on MHD natural convection flow from vertical permeable flat plate with uniform surface heat flux, Applied Mathematics and Mechanics (English Edition). (2011) 32, no. 9, 1127–1146, 2-s2.0-80052587912, https://doi.org/10.1007/s10483-011-1487-9.
Google Scholar
15 Pal D., Talukdar B., Shivakumara I. S., and Vajravelu K., Effects of Hall current and chemical reaction on oscillatory mixed convection-radiation of a micropolar fluid in a rotating system, Chemical Engineering Communications. (2012) 199, 943–965, https://doi.org/10.1080/00986445.2011.616248.
Google Scholar
16 Cogley A. C., Vincenti W. C., and Gilles S. E., Differential approximation for radiation transfer in a nongray gas near equilibrium, American Institute of Aeronautics and Astronautics Journal. (1968) 6, 551–555.
Google Scholar
17 Mansour M. A., Radiative and free-convection effects on the oscillatory flow past a vertical plate, Astrophysics and Space Science. (1990) 166, no. 2, 269–275, 2-s2.0-0010002497, https://doi.org/10.1007/BF01094898.
Google Scholar
18 Hossain M. A. and Takhar H. S., Radiation effect on mixed convection along a vertical plate with uniform surface temperature, Heat and Mass Transfer. (1996) 31, no. 4, 243–248, 2-s2.0-0030129272.
Google Scholar
19 Hossain M. A., Alim M. A., and Rees D. A. S., The effect of radiation on free convection from a porous vertical plate, International Journal of Heat and Mass Transfer. (1999) 42, no. 1, 181–191, 2-s2.0-0345490861, https://doi.org/10.1016/S0017-9310(98)00097-0.
Google Scholar
20 Seddeek M. A., Effects of radiation and variable viscosity on a MHD free convection flow past a semi-infinite flat plate with an aligned magnetic field in the case of unsteady flow, International Journal of Heat and Mass Transfer. (2002) 45, no. 4, 931–935, 2-s2.0-0035910053, https://doi.org/10.1016/S0017-9310(01)00189-2.
Google Scholar
21 Muthucumaraswamy R. and Senthil G. K., Studied the effect of heat and mass transfer on moving vertical plate in the presence of thermal radiation, Journal of Theoretical And Applied Mechanics. (2004) 31, no. 1, 35–46.
Google Scholar
22 Pal D., Heat and mass transfer in stagnation-point flow towards a stretching surface in the presence of buoyancy force and thermal radiation, Meccanica. (2009) 44, no. 2, 145–158, 2-s2.0-63049090053, https://doi.org/10.1007/s11012-008-9155-1.
Google Scholar
23 Aydin O. and Kaya A., Radiation effect on MHD mixed convection flow about a permeable vertical plate, Heat and Mass Transfer. (2008) 45, no. 2, 239–246, 2-s2.0-54149091977, https://doi.org/10.1007/s00231-008-0428-y.
Google Scholar
24 Mohamed R. A., Double-diffusive convection-radiation interaction on unsteady MHD flow over a vertical moving porous plate with heat generation and Soret effects, Applied Mathematical Sciences. (2009) 3, no. 13–16, 629–651, 2-s2.0-67650931811.
Google Scholar
25 Chauhan D. S. and Rastogi P., Radiation effects on natural convection MHD flow in a rotating vertical porous channel partially filled with a porous medium, Applied Mathematical Sciences. (2010) 4, no. 13–16, 643–655, 2-s2.0-77953328047.
Google Scholar
26 Ibrahim S. Y. and Makinde O. D., Radiation effect on chemically reacting magnetohydrodynamics (MHD) boundary layer flow of heat and mass transfer through a porous vertical flat plate, International Journal of Physical Sciences. (2011) 6, no. 6, 1508–1516, 2-s2.0-79957947736.
CAS Google Scholar
27 Pal D. and Mondal H., The influence of thermal radiation on hydromagnetic darcy-forchheimer mixed convection flow past a stretching sheet embedded in a porous medium, Meccanica. (2011) 46, no. 4, 739–753, 2-s2.0-79961024223, https://doi.org/10.1007/s11012-010-9334-8.
Google Scholar
28 Palani G. and Kim K. Y., Influence of magnetic field and thermal radiation by natural convection past vertical cone subjected to variable surface heat flux, Applied Mathematics and Mechanics (English Edition). (2012) 33, 605–620.
Google Scholar
29 Mahmoud M. A. A. and Waheed S. E., Variable fluid properties and ther-28 mal radiation effects on flow and heat transfer in micropolar fluid film past moving permeable infinite flat plate with slip velocity, Applied Mathematics and Mechanics (English Edition). (2012) 33, 663–678.
Google Scholar
30 Aboeldahab E. M. and Elbarbary E. M. E., Hall current effect on magnetohydrodynamic free-convection flow past a semi-infinite vertical plate with mass transfer, International Journal of Engineering Science. (2001) 39, no. 14, 1641–1652, 2-s2.0-0035452655, https://doi.org/10.1016/S0020-7225(01)00020-9.
Google Scholar
31 Abo-Eldahab E. M. and El Aziz M. A., Viscous dissipation and Joule heating effects on MHD-free convection from a vertical plate with power-law variation in surface temperature in the presence of Hall and ion-slip currents, Applied Mathematical Modelling. (2005) 29, no. 6, 579–595, 2-s2.0-17044404988, https://doi.org/10.1016/j.apm.2004.10.005.
Google Scholar
32 Kandasamy R., Periasamy K., and Sivagnana Prabhu K. K., Chemical reaction, heat and mass transfer on MHD flow over a vertical stretching surface with heat source and thermal stratification effects, International Journal of Heat and Mass Transfer. (2005) 48, no. 21-22, 4557–4561, 2-s2.0-23844441535, https://doi.org/10.1016/j.ijheatmasstransfer.2005.05.006.
Google Scholar
33 Muthucumaraswamy R. and Janakiraman B., Mass transfer effects on isothermal vertical oscillating plate in the presence of chemical reaction, International Journal of Applied Mathematics and Mechanics. (2008) 4, no. 1, 66–74.
Google Scholar
34 Sharma P. R. and Singh K. D., Unsteady MHD free convective flow and heat transfer along a vertical porous plate with variable suction and internal heat generation, International Journal of Applied Mathematics and Mechanics. (2009) 4, no. 5, 1–8.
Google Scholar
35 Sudheer Babu M. and Satya Narayan P. V., Effects of the chemical reaction and radiation absorption on free convection flow through porous medium with variable suction in the presence of uniform magnetic field, Journal of Heat and Mass Transfer. (2009) 3, 219–234.
Google Scholar
36 Makinde O. D. and Chinyoka T., Numerical study of unsteady hydromagnetic Generalized Couette flow of a reactive third-grade fluid with asymmetric convective cooling, Computers and Mathematics with Applications. (2011) 61, no. 4, 1167–1179, 2-s2.0-79651469279, https://doi.org/10.1016/j.camwa.2010.12.066.
Google Scholar
37 Pal D. and Talukdar B., Combined effects of Joule heating and chemical reaction on unsteady magnetohydrodynamic mixed convection of a viscous dissipating fluid over a vertical plate in porous media with thermal radiation, Mathematical and Computer Modelling. (2011) 54, no. 11-12, 3016–3036, 2-s2.0-84860389884, https://doi.org/10.1016/j.mcm.2011.07.030.
Google Scholar
38 Singh K. D. and Kumar R., Combined effects of hall current and rotation on free convection MHD flow in a porous channel, Indian Journal of Pure and Applied Physics. (2009) 47, no. 9, 617–623, 2-s2.0-70450177455.
Google Scholar
39 Meyer R. C., On reducing aerodynamic heat transfer rates by magnetohydrodynamic techniques, Journal of the Aerospace Sciences. (1958) 25.
Google Scholar

Citing Literature

All articles

Influence of Hall Current and Thermal Radiation on MHD Convective Heat and Mass Transfer in a Rotating Porous Channel with Chemical Reaction

Abstract

1. Introduction

2. Problem Formulation

3. Method of Solution

4. Amplitude and Phase Difference due to Steady and Unsteady Flow

5. Amplitude and Phase Difference of Shear Stresses due to Steady and Unsteady Flow at the Plate

6. Results and Discussion

7. Conclusions

Nomenclature

Greek Symbols

Acknowledgment

Appendix

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Influence of Hall Current and Thermal Radiation on MHD Convective Heat and Mass Transfer in a Rotating Porous Channel with Chemical Reaction

Abstract

1. Introduction

2. Problem Formulation

3. Method of Solution

4. Amplitude and Phase Difference due to Steady and Unsteady Flow

5. Amplitude and Phase Difference of Shear Stresses due to Steady and Unsteady Flow at the Plate

6. Results and Discussion

7. Conclusions

Nomenclature

Greek Symbols

Acknowledgment

Appendix

References

Citing Literature

Figures

References

Related

Information