Leader-Following Consensus Stability of Discrete-Time Linear Multiagent Systems with Observer-Based Protocols
Abstract
We consider the leader-following consensus problem of discrete-time multiagent systems on a directed communication topology. Two types of distributed observer-based consensus protocols are considered to solve such a problem. The observers involved in the proposed protocols include full-order observer and reduced-order observer, which are used to reconstruct the state variables. Two algorithms are provided to construct the consensus protocols, which are based on the modified discrete-time algebraic Riccati equation and Sylvester equation. In light of graph and matrix theory, some consensus conditions are established. Finally, a numerical example is provided to illustrate the obtained result.
1. Introduction
In recent decades, the cooperate and control problem of distributed dynamic systems has been a challenging research field, owing to its widespread applications in many areas such as swarm of animals [1], collective motion of particles [2], schooling for underwater vehicles [3, 4], neural networks [5, 6], and distributed sensor networks [7].
The consensus problem, as one fundamental problem for coordinated control of multiagent systems, has gained significant attention from different research communities. Consensus problem considers how to design an information interaction protocol between agents and requires all agents to converge to a common value [8, 9]. Based on matrix theory, algebraic graph theory, and control theory, many researchers have acquired abundant results in studying consensus problem of multiagent systems. In [10], the authors proposed a general framework for consensus problem in fixed and switching networks and gave solution to the case with communication time delays. Olfati-Saber et al. established a general model for consensus problems of the multiagent systems and introduced Lyapunov method to reveal the contract with the connectivity of the graph theory and the stability of the system in [11]. Sometimes, it is better to consider a tracking consensus problem by adding a leader which can make all agents reach a command trajectory with any initial condition [12]. The leader-following consensus problem has been addressed in many references [13–17].
Many proposed distributed consensus protocols need to know neighbors’ state information, but it may be difficult to measure this information. To make the system achieve consensus, it often contains an observer in the control protocol, which is used to estimate those unmeasurable state variables. The distributed observer-based control laws were proposed to solve first-order and second-order multiagent consensus problems in [12, 17]. To estimate the general active leader’s unmeasurable state variables, [18] proposed a distributed algorithm for first-order agent, and [19] extended the results of [18] to the time-delay case. The distributed observer-based consensus protocols were addressed to solve multiagent consensus with general linear or linearized agent dynamics in [17, 20–24]. In [25], the author proposed an observer-type consensus protocol to the consensus problem for a class of fractional-order uncertain multiagent systems with general linear dynamics. In [26], the authors proposed distributed reduced-order observer-based protocols to solve consensus problem, which were generalized to solve leader-following consensus problem under switching topology by [27]. The observer-based consensus protocol can be viewed as a special case of the dynamic compensation method, which has been investigated by [28–30].
Discrete-time dynamic systems are commonly involved in the neural network, sampled control, signal filters, and state estimators. The discrete-time neural network was studied by [31–33]. The sampled-data discrete-time coordination of multiagent systems was investigated in [16, 34, 35]. The first-order discrete-time consensus has been investigated by [8, 9, 36–38]. In [39], the authors discussed discrete-time second-order consensus protocols for dynamics with nonuniform and time-varying communication delays under dynamically switching topology. The distributed H∞ consensus problem was studied in [30] to solve multiagent consensus problem with discrete-time high-dimensional linear coupling dynamics subjected to external disturbances. The distributed state-feedback protocols for linear discrete-time multiagent were proposed in [40, 41]. The distributed observer-based protocol was proposed to solve leader-following consensus problem with linear discrete-time dynamics in [23, 42, 43].
Motivated by the above works, we focus our research on a group of agents with discrete-time high-dimensional linear coupling dynamics and directed interaction topology. We propose distributed observer-based protocols for leader-following multiagent systems. The full-order observer and reduced-order observer are adopted to reconstruct the state variables. Contrary to [23] and [40], the gain matrix design approach used in this paper is based on the modified discrete-time algebraic Riccati equations (MDARE) but not the normal discrete-time algebraic Riccati equations. The proposed design method must be feasible if spectral radius of system matrix is not greater than 1. Of course, the proposed design method can be used to construct the consensus protocols provided by [23] and [40]. Further, the separation principle is shown to be valid, from which we can establish consensus condition for closed-loop multiagent systems.
This paper is organized as follows. Section 2 presents the related notations and the problem formulated with graph theory. In Section 3, the distributed state feedback design is considered. In Sections 4 and 5, the distributed full-order and reduced-order observer-based consensus protocols are proposed, respectively, which are the main results of this paper. Section 6 presents a simulation example to illustrate our established results. Finally, the conclusion is given in Section 7.
2. Preliminaries and Problem Formulation
2.1. Notations and Graph Theory
Re(ξ) denotes the real part of ξ ∈ C. Let Rm×n and Cm×n be the set of m × n real matrices and complex matrices, respectively. 1n ∈ Rn is the column vector with all components equal to one. Let I be the identity matrix with compatible dimension. For a given matrix A, aij represents its element of ith row and jth column, AT denotes its transpose, and AH denotes its conjugate transpose. A matrix is said to be Schur-stable if all its eigenvalues are inside unit circle. ρ(A) represents the spectral radius of matrix A. λmax (A) and λmin (A) represent its maximum and minimum eigenvalues of symmetric matrix A, respectively. For symmetric matrices A and B, A > B means that A − B is positive definite, that is, A − B > 0. ⊗ denotes Kronecker product, which satisfies (A ⊗ B)(C ⊗ D) = (AC)⊗(BD).
We describe the interaction relationship among n agents by a simple weighted diagraph 𝒢 = {𝒱, ɛ, W}, where 𝒱 = {v1, v2, …, vn} is the set of vertices and ɛ ⊂ 𝒱 × 𝒱 is the set of edges. If (vi, vj) ∈ ɛ, the vertex vj is called a neighbor of vertex vi, and the index set of neighbors of vertex vi is denoted by 𝒩i = {j∣(vi, vj) ∈ ɛ}. W = [wij] n×n represents weighted adjacency matrix associated with graph 𝒢, where wij > 0 if (vi, vj) ∈ ɛ and wij = 0 otherwise. The degree matrix D = diag {d1, d2, …, dn} of digraph 𝒢 is a diagonal matrix with diagonal elements . Then, the Laplacian matrix of 𝒢 is defined as L = D − W. vi is called globally reachable node if there exists at least a directed path from every other node to node vi in digraph 𝒢. A directed graph 𝒢 has a globally reachable node if and only if there exists a directed spanning tree in 𝒢 (see [9]).
For a multiagent system with leader (labeled as 0), the interaction topology is expressed by graph , which contains graph 𝒢 and vertex v0 and edges from other vertices to vertex v0. Let gi, i = 1,2, …, n, be weight of (vi, v0). gi > 0 if (vi, v0) is an edge of graph and gi = 0 otherwise. Let Gd = diag {g1, g2, …, gn}. The matrix L + Gd has the following property.
Lemma 1 (see [13].)Matrix L + Gd is positive stable if and only if graph has a directed spanning tree with root v0.
2.2. Problem Formulation
The x0(k) is often called as “consensus reference state” and assumed to be available only to a subgroup of the followers. The main objective of leader-following consensus problem is to design distributed consensus protocol to make multiagent system achieve consensus.
Definition 2. The leader-following multiagent system is said to achieve consensus if the state variables of all following agents satisfy lim k→∞ (xi(k) − x0(k)) = 0, i = 1,2, …, n for any initial state. One says that the protocol ui(k) can solve the leader-following consensus problem if the closed-loop system achieves consensus.
2.3. Preliminary Results
Lemma 3 (see [45], [46].)If (A, Q1/2) is detectable, (A, B) is stabilizable, then there exists a δc ∈ [0,1) such that the modified discrete time algebraic Riccati equation (3) has a unique positive-definite solution P for any δc < δ ≤ 1. Furthermore, P = lim k→∞Pk for any initial condition P0 ≥ 0, where Pk satisfies
Remark 4. The MDARE (3) is reduced, respectively, to the well-known discrete-time Riccati equation (DARE) and Stain equation as δ = 1 and δ = 0. The Stain equation has a unique positive-definite solution if A is Schur-stable. It is well known that DARE has a unique positive-definite solution if (A, B) is stablizable. If the involved matrix A is not Schur-stable, it is easy to see that 0 < δc ≤ 1. More details for issue δc can be referenced to [45]. Moreover, if the matrix A has no eigenvalues with magnitude larger than 1 and (A, C) is detectable, MDARE (3) has a unique positive-definite solution P for any δ satisfying 0 < δ ≤ 1.
Lemma 5. For a given δ satisfying δc < δ ≤ 1, let P be the unique positive-definite solution of the MDARE (3). Choose a feedback matrix K = (I + BTPB) −1BTPA. Then, A − sBK is Schur-stable for any .
Proof. From the MDARE (3), we have
3. Distributed State Feedback Design
In this section, we investigate the multiagent consensus via state variable feedback control, which has been addressed by [23]. Here, we also use the control protocol proposed by [23] and provide a new design approach to construct the feedback gain matrix.
Definition 6 (see [23].)A covering circle related to matrix Γ is a closed circle in the complex plane centered at c0 ∈ R and for all i = 1,2, …, n.
Then, we provide a new design technique to construct feedback gain matrix K, which is presented in the following theorem.
Theorem 7. For multiagent system (1) and (2), assume that the interconnection topology has a directed spanning tree with root v0. If there exists a covering circle such that
Proof. From (10), we know δ > δc, which means that the MDARE (3) has a unique positive-definite solution P. Any λi satisfies |λi − c0 | ≤ r0. Thus, . According to Lemma 5, all A − c1λiBK, i = 1,2, …, n are Schur-stable.
Let U be a Schur transformation matrix of Γ such that
Remark 8. From condition (9), it is required that 0 < c0 < r0, which means that the covering circle should be located in the open right half plane. Moreover, the small enough r0/c0 will guarantee that the MDARE (3) is solvable, which is the key point in the proposed design approach. The weight parameter in the feedback law (7) need not take c1(1 + di + gi) −1, which can be selected as c1(di + gi) −1, c1, and so on as long as there exists a covering circle for the related matrix c1Γ that satisfies the condition (9).
According to Theorem 7, we present the following corollary for this special case.
Corollary 9. For multiagent system (1) and (2) with ρ(A) ≤ 1, assume that the interconnection topology has a directed spanning tree with root v0. Take and solve the MDARE (3) to get the unique positive-definite solution P. Choose K = (I + BTPB) −1BTPA and C1 = 1. Then, the distributed feedback control (7) guarantees that all following agents can track leader.
4. Consensus Protocol Design with Full-Order Observer
- (i)
Local estimation law for agent i:
(16)where zi(k) ∈ Rm is the protocol state, is the constructed variable to estimate xi(k), and F ∈ Rm×m, G ∈ Rm×q, and T ∈ Rm×m are the designed parameter matrices. - (ii)
Neighbor-based feedback control law for agent i:
(17)where the neighborhood disagreement observer error ηi(k) of agent i is denoted as(18)and K is a given feedback gain matrix.
Next, an algorithm is provided to select the parameter matrices used in estimation law (16).
Algorithm 10. Given that (A, C) is observable. The parameter matrices F, G, and T used in estimation law (16) can be constructed as follows.
- (1)
Select a Schur-stable m × m matrix F with a set of desired eigenvalues that contain no eigenvalues in common with those of A.
- (2)
Select G ∈ Rm×q randomly such that (F, G) is controllable.
- (3)
Solve Sylvester equation
(19)
Denote and . Then, after manipulations and combining (1) and (16), we can obtain
Theorem 11. For multiagent system (1) and (2), assume that the interconnection topology has a directed spanning tree with root v0. If there exists a covering circle such that
Remark 12. Of course, when system matrix A satisfies ρ(A) ≤ 1, we can also establish similar corollaries as Corollary 9 in this section and the next section. In [23], three different observer/controller architectures are proposed for dynamic output feedback regulator design. Besides design feedback matrix K, another key technique is to choose an observer gain matrix L which makes In ⊗ A − c1Γ ⊗ (LC) Schur-stable. By using duality property, solve the following MDARE:
5. Consensus Protocol Design with Reduced-Order Observer
- (i)
Local reduced-order estimation law for agent i:
(27)where vi(k) ∈ Rm−q is the protocol state, F ∈ Rm−q×m−q, and G ∈ Rm−q×q and T ∈ Rm−q×m are parameter matrices. - (ii)
Neighbor-based feedback control law for agent i:
(28)where the disagreement error ζi(k) of agent i is given as(29)and K is a gain matrix.
Similarly, an algorithm is presented to design the same parameter matrices used in the protocols (27) and (28).
Algorithm 13. Given that (A, C) is observable. The parameter matrices F, G, T, Q1, and Q2 can be constructed as follows.
- (1)
Select a Schur matrix F ∈ R(m−q)×(m−q) with a set of desired eigenvalues that contain no eigenvalues in common with those of A.
- (2)
Select G ∈ R(m−q)×q randomly such that (F, G) is controllable.
- (3)
Solve Sylvester equation
(30)
- (4)
Compute matrices Q1 ∈ Rm×q and Q2 ∈ Rm×(m−q) by .
Now, we present the result related to reduced-order observer.
Theorem 14. For multiagent system (1) and (2), assume that the interconnection topology has a directed spanning tree with root v0. If there exists a covering circle such that
Proof. To analyze convergence, denote ei(k) = xi(k) − x0(k) and ɛi = vi(k) − Tx0(k). Then, the dynamics of ei(k) and ɛi(k) satisfy
Let , which is nonsingular, and . By step (2) of Algorithm 13, we have
6. Simulation Example
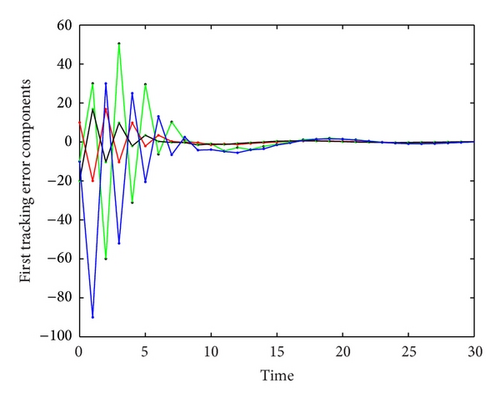

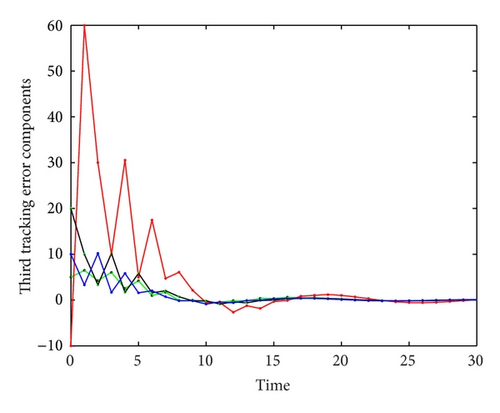

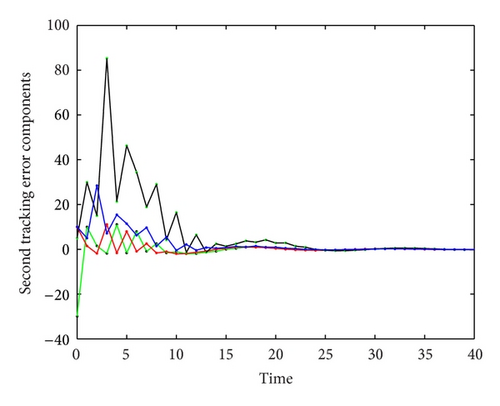
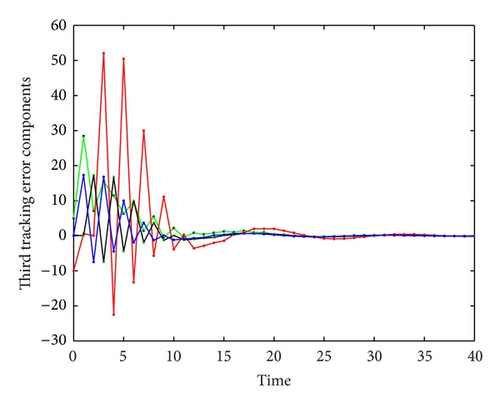
7. Conclusions
This paper solves a leader-following consensus problem of discrete-time multiagent system with distributed controllers and observers. We provide a general framework for designing distributed consensus protocols by applying full state feedback information and measured output feedback information. Furthermore, we propose a reduced-order observer-based protocol to solve the leader-following consensus problem. The interconnection topology is modeled by graph, whose connectivity is a key factor to guarantee that the multiagent achieves consensus. The consensus problem is transformed into the stability problem of error dynamical system, which also preserves the property of the separation principle. The gain matrices can be designed by solving the MDARE and the Sylvester equation. Presented results could be generalized to switching and jumping interaction topology in future work.
Acknowledgments
This work was supported by the Zhejiang Provincial Natural Science Function of China under Grant no. LY13F030048 and the National Natural Science Function of China under Grant nos. 61074123, 61174063.




