Abstract and Applied Analysis
Volume 2013, Issue 1 324869
Research Article
Open Access

Solution of Boundary Layer Problems with Heat Transfer by Optimal Homotopy Asymptotic Method

H. Ullah, 

Corresponding Author

H. Ullah

Department of Mathematics, Abdul Wali Khan University Mardan, Mardan 23200, Pakistan awkum.edu.pk

Search for more papers by this author
S. Islam, 

S. Islam

Department of Mathematics, Abdul Wali Khan University Mardan, Mardan 23200, Pakistan awkum.edu.pk

Search for more papers by this author
M. Idrees, 

M. Idrees

Department of Mathematics, Abdul Wali Khan University Mardan, Mardan 23200, Pakistan awkum.edu.pk

Search for more papers by this author
M. Arif, 

M. Arif

Department of Mathematics, Abdul Wali Khan University Mardan, Mardan 23200, Pakistan awkum.edu.pk

Search for more papers by this author
First published: 17 September 2013
https://doi.org/10.1155/2013/324869
Citations: 13
Academic Editor: Carlo Bianca

Abstract

Application of Optimal Homotopy Asymptotic Method (OHAM), a new analytic approximate technique for treatment of Falkner-Skan equations with heat transfer, has been applied in this work. To see the efficiency of the method, we consider Falkner-Skan equations with heat transfer. It provides us with a convenient way to control the convergence of approximate solutions when it is compared with other methods of solution found in the literature as finite difference (N. S. Asaithambi, 1997) and shooting method (Cebeci and Keller, 1971). The obtained solutions show that OHAM is effective, simpler, easier, and explicit.

1. Introduction

Most of the problems in engineering sciences are nonlinear, particularly some of heat transfer problems. Limited analytic methods are presented for the solution of such problems in the literature. Therefore, the researcher’s profound attention is to hunt some new analytic methods for the solution of the problems. Most of the methods like Adomian Decomposition Method (ADM) [1], Variational Iteration Method (VIM) [2], Differential Transform Method (DTM) [3], Radial basis function [4] and Homotopy Perturbation Method (HPM) [5], are used for the solution of weakly nonlinear problems, and limited for strongly nonlinear problems. For the solution of the strongly nonlinear problems the perturbation methods were studied [6–8]. These methods comprise a small parameter which cannot be found easily. To overcome this issue, some new analytic methods such as Artificial Parameters Method [9], Homotopy Analysis Method (HAM) [10], and Homotopy Perturbation Method (HPM) [5] were introduced. These methods pooled the homotopy with the perturbation techniques. Recently, Marinca et al. introduced Optimal Homotopy Asymptotic Method (OHAM) [11–15] for the solution of nonlinear problems which made the perturbation methods independent of the assumption of small parameters.

The Falkner-Skan equation has been considered in the last forty years due to its importance in the boundary layer theory. The boundary layer theory plays a vital role in the diverse area of engineering and scientific applications. The solution of the Falkner-Skan equation has been studied numerically first by Hartree [16]. Smith and Cebeci [17, 18] solved this equation by shooting method. Maksyn [19] solved the Falkner-Skan equation by analytic approximation. Asithambi [20–22] found its solution by finite differences, Liao [23] applied homotopy analysis to solve Falkner-Skan equation, and recently Vera [24] found its solution by Fourier series. An important case is the Blasius equation. This problem was solved by Rosales and Valencia [25] using Fourier series. Boyd [26] found the solution of Falkner-Skan equation by numerical method. An enormous amount of research work has been invested in the study of nonlinear boundary value problems [27–38]. In this paper, we will deal with the Falkner-Skan equations with heat transfer, a nonlinear boundary value problem [24] in different forms.

The motivation of this paper is to enhance OHAM for the solution of Falkner-Skan equation with heat transfer. In [11–15], OHAM has been proved to be useful for obtaining an approximate solution of nonlinear boundary value problems. In this work, we have proved that OHAM is also useful and reliable for the solution of the Falkner-Skan equation with heat transfer, hence showing its validity and great potential for the solution of transient physical phenomenon in science and engineering.

In the succeeding section, the basic idea of OHAM [11–15] is formulated for the solution of boundary value problems arising in heat transfer. In Section 3, the effectiveness of the enhanced formulation of OHAM for Falkner-Skan equation with heat transfer has been studied. Two special cases [24] of Falkner-Skan equation with heat transfer problems have been analyzed.

2. Basic Mathematical Theory of OHAM

Let us consider the following differential equation:
()
along with boundary conditions of the form
()
where ℒ is the linear operator, u(t) is an unknown function, h(t) is a known function, 𝒩(u(t)) is a nonlinear differential operator, and ℬ is a boundary operator.
According to OHAM, one can construct an optimal homotopy ϕ(t, q): Ω × [0,1] → ℜ which satisfies
()
()
where q ∈ [0,1] is an embedding parameter, ϕ(t, q) is an unknown function, and H(q) is a nonzero auxiliary function. The auxiliary function H(q) is nonzero for q ≠ 0 and H(0) = 0. Equation (3) is the structure of OHAM homotopy.
It is defined that
()
respectively. Thus, as q varies from 0 to1, the solution ϕ(t, q) varies from u0(t) to u(t), where u0(t) is obtained from (1) and (2) for p = 0 as follows:
()
Next, we choose auxiliary function H(q) in the form
()
where C1,   C2,   C3, … are constants and can be found latter.
To obtain an approximate solution, we expand ϕ(t, q, Ci) by Taylor’s series about q in the following form:
()
Now substituting (8) into (1) and (2) and equating the coefficient of like powers of q, we obtain the zeroth-order problem given by (6), the first- and second-order problems given by (9)–(11), respectively, and the general governing equations for uk(t) given by (11):
()
()
()
where 𝒩k−i(u0(t), u1(t), …, uk−i(t)) is the coefficient of qk−i in the expansion series of 𝒩(ϕ(t, q)) about the embedding parameter p as follows:
()

It should be underscored that the uk for k ≥ 0 are governed by the linear equations with linear boundary conditions that come from the original problem, which can be easily solved.

It has been observed that the convergence of the series (8) depends upon the auxiliary constants C1, C2, …. If it is convergent at q = 1, one has
()
Substituting (13) into (1), it results in the following expression for residual:
()

If R(t, C1, C2, …, Ci) = 0, then is the exact solution of the problem. Generally it does not happen, especially in nonlinear problems.

For the determinations of auxiliary constants, Ci,   i = 1,2, …, m, there are different methods like Galerkin’s method, Ritz method, least squares method, and collocation method. One can apply the method of  least squares as follows:
()
where a and b are two values, depending on the nature of the given problem.
The auxiliary constants Ci,   i = 1,2, …, m can be optimally found from
()
The mth order approximate solution can be obtained bythese constants. The constants Ci can also be determined by another method as follows:
()

The convergence of OHAM is directly proportional to the number of optimal constants C1, C2, … which is determined by (16).

It is easy to observe [13] that the Homotopy Perturbation Method (HPM) proposed by He [4] is a special case of (3) when H(q) = −q, and on the other hand, the Homotopy Analysis Method (HAM) proposed by Liao [11] is another special case of (3) when H(q) = qℏ where ℏ is chosen from “ℏ-curves” [12].

3. Application of OHAM to Falkner-Skan Equations with Heat Transfer

To demonstrate the effectiveness of OHAM formulation, two models are studied.

Model 1 (see [23].)When an incompressible fluid passes in the vicinity of solid boundaries, the Navier-Stokes equations may be reduced drastically into the boundary layer equations:

()
where Ue(x) is the free stream velocity, u and v are velocity components in x- and y-directions, and υ is the kinematic viscosity. In case of two-dimensional flow, the incompressible boundary layer flow over a wedge, when the free stream velocity is of the form Ue(x) = Kxm, is the following similarity transformation:
()

Using (19) into (18), we obtained the Falkner-Skan equation

()
along with boundary conditions
()

According to (1), we have

()

The boundary conditions are

()

Applying the method formulation mentioned in Section 2 leads to the following.

Zeroth-Order Problem. Consider

()
()
from which we obtain
()

First-Order Problem. Consider

()
()

Its solution is

()

Second-Order Problem. Consider

()
with BC
()
whose solution is
()

Adding (25), (27), and (29), we obtain

()
where
()

For the computation of the constants C1 and C2 applying the method of least square mentioned in (14)–(16), we get

()

Putting these values in (30), we obtained the approximate solution of the form

()

Now consider the energy equation of an incompressible fluid which passes through the vicinity of the solid boundaries:

()

Upon using the transformation in (19) into (37), we obtained

()
with boundary conditions
()
where “a” is the thermal diffusivity and Pr is the prandtl number.

Applying the method formulated in Section 2 leads to the following.

Zeroth-Order Problem. Consider

()

Its solution is

()

First-Order Problem. Consider

()

whose solution is

()
Second-Order Problem. Consider
()
We obtain the following solution:
()
Adding (41), (43), and (45), we obtain
()
where
()
Using (46) in (38) and applying the method of least square, we obtain
()
Substituting these values in (46) for β = 1 and Pr = 10, we obtain
()

Model 2 (see [23].)In case of β = 0 in (52), we obtain the Blasius equation which is the famous equation of fluid dynamics and represent the problem of an incompressible fluid that passes through on a semi-infinite flat plate.

One has

()
()

According to (1), we define the operators

()
where f′′(η) and f′′′(η) represent the second and third derivatives of f(η) with respect to η.

Applying the method formulated in Section 2 leads to the following.

Zeroth-Order Problem. Consider
()
()
Its solution is
()
First-Order Problem. Consider
()
whose solution is
()
Second-Order Problem. Consider
()
We obtain the following solution:
()
Third-Order Problem. Consider
()
Its solution is
()
From (53), (57), (59), and (61), we obtain
()
where
()
Using (62) in (50) and applying the technique as discussed in (14)–(16), we obtain
()
Substituting these values in (62), we have
()

4. Results and Discussions

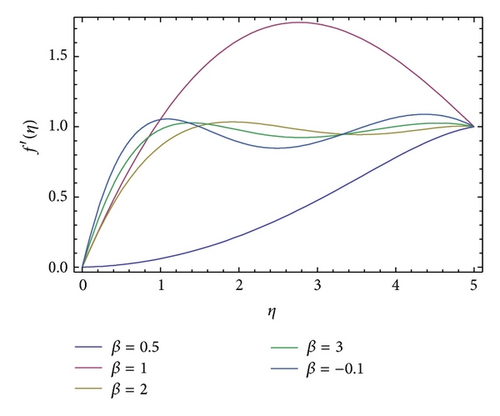
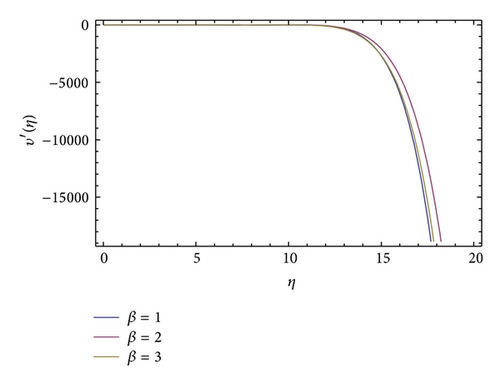
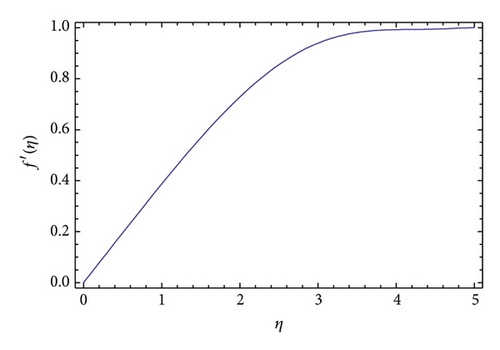
The formulation presented in Section 2 provides highly accurate solutions for the problems demonstrated in Section 3. We have used Mathematica 7 for most of our computational work. In Table 1, we have presented the initial slope f′′(0) for different values of β obtained by OHAM. Table 1 shows that the results obtained by OHAM are in excellent agreement with the results found in the literature. Table 1 shows a benchmark for the initial slope f′′(0) found by different authors. It is found that the method present in this work is very good and provides the same values that optimized numerical methods with which it is compared. Figure 1 shows the variation of the function f′(η) against η for different values of β with OHAM, while Figure 2 shows the variation of the function υ′(η) with respect to η for different values of β. Table 2 shows the solution of the Blasius equation obtained by the present method. In order to verify the accuracy of the present method, we have compared the results obtained by OHAM to the results available in the literature and found an excellent agreement. Figures 2 and 3 show the variation of f′(η) with respect to η for the Blasius equation which is identical to results in the literature [41].

Table 1. Initial slope f′′(0) obtained by OHAM for different values of β.
β Hartree [16] Asaithambi [22] Asaithambi [21] Salama [39] Zhang [40] Vera [24] OHAM
2 1.687 1.687222 1.687218 1.687218 1.687218 1.687218 1.67054
1 1.233 1.23589 1.232588 1.232588 1.232587 1.232587 1.23567
0.5 0.927 0.927682 0.927680 0.927680 0.927680 0.927680 0.92697
−0.1 0.319 0.319270 0.319270 0.319270 0.319270 0.319270 0.31927
Table 2. Solution of the Blasius equation by OHAM.
η f(η) f′(η) f′′(η)
0.0 0.000000000 0.000000000 3.90295 × 10−1
0.5 4.87655 × 10−2 1.94934 × 10−1 3.88588 × 10−1
1.0 1.94467 × 10−1 3.86900 × 10−1 3.76782 × 10−1
1.5 4.33963 × 10−1 5.68522 × 10−1 3.45926 × 10−1
2.0 7.59425 × 10−1 7.28781 × 10−1 2.90680 × 10−1
2.5 1.15707 × 100 8.55368 × 10−1 2.12781 × 10−1
3.0 1.60768 × 100 9.39646 × 10−1 1.24115 × 10−1
3.5 2.08955 × 100 9.81346 × 10−1 4.67757 × 10−2
4.0 2.58389 × 100 9.92571 × 10−1 5.82245 × 10−3
4.5 3.08065 × 100 9.94745 × 10−1 8.42702 × 10−3
5.0 3.57943 × 100 1.0000000000 6.18202 × 10−4
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
f′(η) for different values of β.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
υ′(η) for different values of β.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Plot of f′(η) with respect to η.

5. Conclusion

In this work, we have seen the effectiveness of OHAM [11–15] to Falkner-Skan, Energy and Blasius equations. By applying the basic idea of OHAM to Falken-Skan, Energy and Blasius equations, we found that it is simpler in applicability and, more convenient to control convergence and involved less computational overhead. Therefore, OHAM shows its validity and great potential for the solution Falken-Skan, Energy and Blasius equations, with heat transfer problems arising in science and engineering.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.