Volume 2013, Issue 1 320703

Research Article

Open Access

Observer-Based Robust H_∞ Control for Switched Stochastic Systems with Time-Varying Delay

Guoxin Chen,

Guoxin Chen

School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China njust.edu.cn

Search for more papers by this author

Zhengrong Xiang,

Corresponding Author

Zhengrong Xiang

[email protected]

School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China njust.edu.cn

Search for more papers by this author

Hamid Reza Karimi,

Hamid Reza Karimi

orcid.org/0000-0001-7629-3266

Department of Engineering, Faculty of Engineering and Science, University of Agder, 4898 Grimstad, Norway uia.no

Search for more papers by this author

Guoxin Chen,

Guoxin Chen

School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China njust.edu.cn

Search for more papers by this author

Zhengrong Xiang,

Corresponding Author

Zhengrong Xiang

[email protected]

School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China njust.edu.cn

Search for more papers by this author

Hamid Reza Karimi,

Hamid Reza Karimi

orcid.org/0000-0001-7629-3266

Department of Engineering, Faculty of Engineering and Science, University of Agder, 4898 Grimstad, Norway uia.no

Search for more papers by this author

First published: 08 September 2013

https://doi.org/10.1155/2013/320703

Citations: 3

Academic Editor: Lixian Zhang

Share a link

Email
Wechat
Bluesky

Abstract

This paper investigates the problem of observer-based robust H_∞ control for a class of switched stochastic systems with time-varying delay. Based on the average dwell time method, an exponential stability criterion for switched stochastic delay systems is proposed. Then, H_∞ performance analysis and observer-based robust H_∞ controller design for the underlying systems are developed. Finally, a numerical example is presented to illustrate the effectiveness of the proposed approach.

1. Introduction

Switched systems are a kind of hybrid dynamical systems composed of a set of continuous-time subsystems or discrete-time subsystems and a switching law that orchestrates the switching between them. Switched systems have attracted increasing attention during the past decades because of their wide applications in real-world systems, such as robot control systems [1], networked control systems [2, 3]. Many useful results on stability analysis and control synthesis for such systems have been reported in [4–8]. For example, H_∞ control of switched linear discrete-time systems with polytopic uncertainties was investigated in [8].

It is well known that the time delay phenomenon is frequently encountered in engineering and social systems, and the existence of which may cause instability or undesirable system performance. Therefore, many research efforts have been devoted to the study of switched time delay systems [9–15]. On the other hand, stochastic systems have attracted considerable attention during the past several decades. Early results can be found in [16], and the H_∞ control problem of stochastic systems with time delay was investigated in [17, 18]. The study on H₂/H_∞ control of stochastic system was developed in [19]. Stability analysis on stochastic system with multiple delays was proposed in [20]. Moreover, some results on switched stochastic systems with and without time delay have been obtained (see [21–25] and the references cited therein).

In many real-world systems, state feedback control will fail to guarantee the stabilization because the states of the systems are not all measurable [26]. One of the key approaches to solve the problem is to reconstruct the states of the systems and realize the required feedback control. Hence, the observer-based control has been an interesting topic in control theory. Some results on observer-based control for stochastic delay systems or Markovian jump systems have been presented in [27–29]. However, to the best of our knowledge, the problem of observer-based robust H_∞ control for switched stochastic systems with time delay has not been fully studied, which motivates the present study.

In this paper, we aim to design an observer-based robust H_∞ controller for switched stochastic systems with time delay such that the closed-loop system is mean-square exponentially stable with H_∞ performance. The major contributions of the work can be summarized as follows: (1) a new Lyapunov-Krasovskii functional candidate is introduced to derive the exponential stability of switched stochastic systems with time delay, and the free-weighting matrix method is employed to reduce the conservatism; (2) an observer-based robust H_∞ controller design scheme for the underlying systems is proposed.

The remainder of the paper is organized as follows. In Section 2, problem statement and some useful lemmas are given. In Section 3, the main results are presented. In Section 4, a numerical example is given to illustrate the effectiveness of the proposed approach. Finally, concluding remarks are provided in Section 5.

Notation. In this paper, the superscript “T” denotes the transpose, and the symmetric term in a matrix is denoted by ∗. The notation X > Y (X ≥ Y) means that X − Y is positive definite (positive semidefinite, respectively). Rⁿ denotes the n-dimensional Euclidean space. ∥x(t)∥ denotes the Euclidean norm. |a| denotes the absolute value of a. L₂[t₀, ∞) is the space of square integrable functions on [t₀, ∞), and t₀ is the initial time. λ_max(P) and λ_min(P) denote the maximum and minimum eigenvalues of P, respectively. A⁺ denotes the Moore-Penrose pseudoinverse of A. I is the identity matrix. diag {a_i} denotes a diagonal matrix with the diagonal elements a_i, i = 1,2, …, n.

2. Problem Formulation and Preliminaries

Consider the following switched stochastic system with time delay:

()

where x(t) ∈ Rⁿ is the state vector, φ(t) ∈ Rⁿ is the initial state function, u(t) ∈ R^l is the control input, v(t) ∈ R^p is the disturbance input which is assumed to belong to L₂[t₀, ∞], y(t) ∈ R^r is the measurable output, z(t) ∈ R^q is the controlled output, and w(t) is a one-dimensional zero-mean Wiener process on a probability space (Ω F P) and satisfies

()

where Ω is the sample space, F is σ-algebras of subsets of the sample space, P is the probability measure on F, and E{·} is the expectation operator. τ(t) is the time delay satisfying

()

where τ and τ_d are known constants.

The function

is a switching signal which is deterministic, piecewise constant, and right continuous. The switching sequence can be described as σ : {(t₀, σ(t₀)), (t₁, σ(t₁)), …, (t_k, σ(t_k))},

, where t₀ is the initial instant and t_k denotes the kth switching instant. Moreover, σ(t) = i means that the ith subsystem is activated. For all

, B_i, C_i, J_i, and G_i are known real-value matrices with appropriate dimensions,

, and

are uncertain real matrices with appropriate dimensions and can be written as

()

where

, A_i, A_τi, D_i, H_i, E_1i, E_2i, and E_3i are known real-value matrices with appropriate dimensions, and F_i(t) is an unknown time-varying matrix that satisfies

()

The state feedback controller is designed as u(t) = K_σ(t)x(t). In actual operation, however, the states of the systems are not all measurable. The following switched system is constructed to estimate the state of system (1a), (1b), (1c), and (1d):

()

where

is the estimation of x(t),

is the observer output, and ϕ(t) ∈ Rⁿ is the initial observer state function. The real state feedback controller becomes

. L_i and K_i are the observer gains and controller gains to be determined, respectively.

Remark 1. It is noted that the observer-based H_∞ control for stochastic systems or Markovian jump systems was considered in [27–29]. However, the results in the aforementioned papers cannot be directly applied to the switched stochastic system considered in the paper. This motivates our study. Also, the proposed observer in (6a), (6b), and (6c) is a switching observer, which is different from the existing ones given in [27–29].

From systems (1a), (1b), (1c), and (1d) and (6a), (6b), and (6c), we can obtain the following augmented closed-loop system:

()

where

denotes the state estimated error.

For σ(t) = i, the parameters of system (7a), (7b), and (7c) are given as follows:

()

Assumption 2. B_i is full row rank, for all .

Definition 3. System (1a), (1b), (1c), and (1d) with v(t) = 0 is said to be mean-square exponentially stable under the switching signal σ(t) if there exist scalars κ > 0 and α > 0, such that the solution x(t) of the system satisfies

()

Definition 4 (see [24].)For any T₂ > T₁ ≥ t₀, let N_σ(T₁, T₂) denote the switching number of σ(t) on an interval [T₁, T₂). If

()

holds for given constants N₀ ≥ 0 and T_α > 0, then the constant T_α is called the average dwell time. As commonly used in the literature, some chooses N₀ = 0.

Definition 5 (see [30].)For any λ > 0 and γ > 0, system (7a), (7b), and (7c) is said to be mean-square exponentially stable with a prescribed weighted H_∞ performance level γ if the following conditions are satisfied:

(1)
when v(t) = 0, system (7a), (7b), and (7c) is mean-square exponentially stable;
(2)
under the zero initial condition, the output z(t) satisfies
()

Lemma 6 (see [31].)For any positive symmetric constant matrix M ∈ R^n×n and a scalar r > 0, if there exists a vector functiong : [0, r] → Rⁿ such that integrations in the following are well defined, then the following inequality holds

()

Lemma 7 (see [32].)Let U, V, W, and X be constant matrices of appropriate dimensions with X satisfying X = X^T, then for all V^TV ≤ I, X + UVW + W^TV^TU^T < 0 if and only if there exists a scalar ε > 0 such that X + εUU^T + ε⁻¹W^TW < 0.

The objective of this paper is to design an observer-based robust H_∞ controller for switched stochastic delay system (1a), (1b), (1c), and (1d) such that the augmented closed-loop system (7a), (7b), and (7c) is mean-square exponentially stable with a prescribed weighted H_∞ performance level γ.

3. Main Results

3.1. Stability Analysis

In this subsection, in order to obtain the main results, we first focus on the problem of stability analysis for the following switched stochastic systems with time delay

()

Theorem 8. For a given scalar α > 0, if there exist symmetric positive definite matrices P_i, Q_i, and R_i and any matrices S_i such that

()

then system (13a) and (13b) is mean-square exponentially stable under arbitrary switching signal with the average dwell time

()

where μ, χ, and λ satisfy

()

Proof. Let Y(t) = A_σ(t)x(t) + A_τσ(t)x(t − τ(t)), then (13a) can be described as

()

Choose the following Lyapunov functional candidate for the ith subsystem

()

where

()

For the sake of simplicity, V_i(t, x(t)) is written as V_i(t) in this paper. According to Itô’s formula, along the trajectory of the ith subsystem, we have

()

where

()

According to Lemma 6, we have

()

Integrating both sides of (18) from t − τ(t) to t, we have

()

Thus,

()

where

Combining (21)–(25) leads to

()

where

()

By using the Schur complement, we obtain from (14) that

()

According to (26), one obtains that

()

Then, taking mathematical expectation, we have

()

From (16) and (19), we obtain that

()

Let σ(t_k) = i. Then, using formula, we can obtain that for t ∈ [t_k, t_k+1),

()

Notice that

()

Thus, it can be obtained that

()

where

()

Noticing that E{V(t)} ≤ sup _{−τ≤θ≤0} E{V(t + θ)}, one gets

()

For any t ∈ [t_k, t_k+1), from (16) and (36), it follows that

()

When (15) holds, noticing that N_σ(t₀, t)≤(t − t₀)/T_α, one has

()

where

The proof is completed.

Remark 9. In the derivation of Theorem 8, a new Lyapunov-Krasovskii functional candidate is constructed for the stability analysis of switched stochastic systems with time delay, and it is different from the ones given in [9–15]. Also, the free-weighting matrix method is utilized to reduce the conservatism.

Remark 10. If μ = 1 in (15), which leads to P_i = P_j, Q_i = Q_j, and R_i = R_j, for all , then system (13a) and (13b) possesses a common Lyapunov function, and the switching signals can be arbitrary.

When w(t) = 0, system (13a) and (13b) becomes the following switched system with time delay:

()

From Theorem 8, we can readily get the exponential stability criterion for switched system (39a) and (39b).

Corollary 11. Consider system (39a) and (39b), for a given scalar α > 0, if there exist symmetric positive definite matrices P_i, Q_i, and R_i and any matrices S_i such that

()

then system (39a) and (39b) is exponentially stable under arbitrary switching signal with the average dwell time scheme (15).

3.2. H_∞ Performance Analysis

In the sequel, we will investigate the problem of H_∞ performance analysis for switched stochastic systems with time delay. Consider the following system:

()

Theorem 12. For a given scalar α > 0, if there exist symmetric positive definite matrices P_i, Q_i, and R_i and any matrices S_i such that

()

then system (41a), (41b), and (41c) is mean-square exponentially stable with a weighted prescribed H_∞ performance level γ under arbitrary switching signal with the average dwell time

()

where μ, χ, and λ satisfy

()

Proof. We can easily obtain that (14) is satisfied if (42) holds. Thus, system (41a), (41b), and (41c) with v(t) = 0 is mean-square exponentially stable.

When v(t) ≠ 0, let

()

Choosing the same Lyapunov functional candidate as (19) and following the proof line of Theorem 8, we have

()

where

()

and ℒV_i(t) satisfies

()

Using the Schur complement, from (42), we get

()

It follows that

()

From (44), we obtain that

()

For any t ∈ [t_k, t_k+1), using formula and taking the mathematical expectation, one has

()

Under the zero initial condition, we obtain that

()

According to (46), one has

()

Multiplying both sides of (55) by leads to

()

Noticing that N_σ(t₀, s)≤(s − t₀)/T_α and T_α ≥ τ + ln (χμ)/λ ≥ ln μ/λ, one obtains that

()

When t → ∞, the following inequality is derived:

()

The proof is completed.

3.3. Observer-Based Robust H_∞ Stabilization

Now, we are in a position to design an observer-based robust H_∞ controller for system (1a), (1b), (1c), and (1d) such that the augmented closed-loop system (7a), (7b), and (7c) is mean-square exponentially stable with a prescribed weighted H_∞ performance level γ. Based on Theorem 12, a sufficient condition for the existence of such a controller is presented in the following theorem.

Theorem 13. Consider system (1a), (1b), (1c), and (1d), for a given scalar α > 0, if there exist scalars ε_i > 0, symmetric positive definite matrices P_i, Q_i, and R_i, and any matrices , Y_i, and Z_i such that, for all ,

()

then there exists an observer-based controller such that system (7a), (7b), and (7c) is mean-square exponentially stable with a prescribed weighted H_∞ performance level γ under arbitrary switching signal with the average dwell time

()

where μ, χ, and λ satisfy

()

Moreover, if the above conditions have a feasible solution, the controller gain matrices and the observer gain matrices can be obtained by and .

Proof. According to Theorem 12, we get that system (7a), (7b), and (7c) is mean-square exponentially stable with a weighted H_∞ performance level γ if the following inequality is satisfied:

()

where

, and

are symmetric positive definite matrices with appropriate dimensions.

Then, we have

()

where

()

From Lemma 7, we have

()

Choose

, and

, and let Z_i = P_iB_iK_i and Y_i = P_iL_i. By using the Schur complement, we can obtain that (67) is equivalent to (59).

Thus, according to Theorem 12, we obtain from (59)–(62) that system (7a), (7b), and (7c) is mean-square exponentially stable with a weighted H_∞ performance level γ. Moreover, we can obtain the controller gain matrices and the observer gain matrices .

The proof is completed.

Remark 14. An observer-based H_∞ controller design scheme is proposed in the paper. Compared with the existing results presented in [27–29], a remark advantage of the work is that the proposed observer is mode-dependent, which means that each subsystem has its individual observer. Moreover, the proposed observer not only ensures the convergence of the estimated error of each subsystem, but also guarantees that the estimated error of the whole system converges to zero exponentially.

In Theorem 13, when we choose that Q_i = R_i = P_i, it is not difficult to get that β_i = 1 and χ = χ_i = 1 + τ(1 + τ)(e^λτ − 1), for all . Then, the following corollary is derived.

Corollary 15. Consider system (1a), (1b), (1c), and (1d), for a given scalar α > 0, if there exist scalars ε_i > 0, symmetric positive definite matrices P_i > 0, and matrices , Y_i, and Z_i such that, for all ,

()

then there exists an observer-based robust H_∞ controller such that system (7a), (7b), and (7c) is mean-square exponentially stable with a prescribed weighted H_∞ performance level γ under arbitrary switching signal with the average dwell time

()

where μ, χ, and λ satisfy

()

Moreover, the controller gain matrices are , and the observer gain matrices are .

4. Numerical Example

Consider system (1a), (1b), (1c), and (1d) with the following parameters

()

The disturbance input

, and τ(t) = 0.3 + 0.2sint; by calculation, we can obtain that

and τ(t) ≤ τ = 0.5. Choosing α = 1.4, γ = 1.0 and solving the LMIs in Corollary 15, we have

()

Then, we can obtain the following observer gain matrices:

()

and the controller gain matrices

()

Moreover, we have μ = 4.3051, λ = 0.7, χ = 1.3143, and . Taking , and letting , t ∈ [−0.5,0), , and , and simulation results are shown in Figures 1–5.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Switching signal.

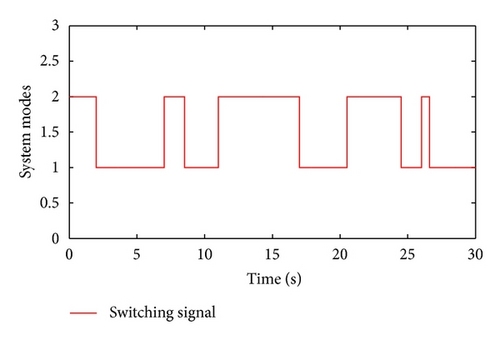
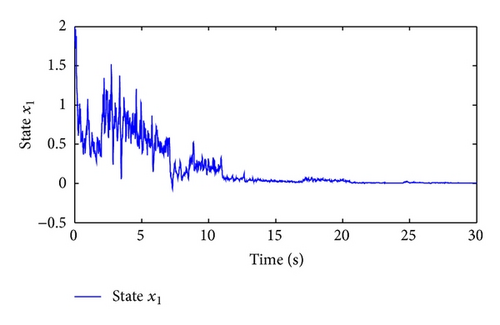
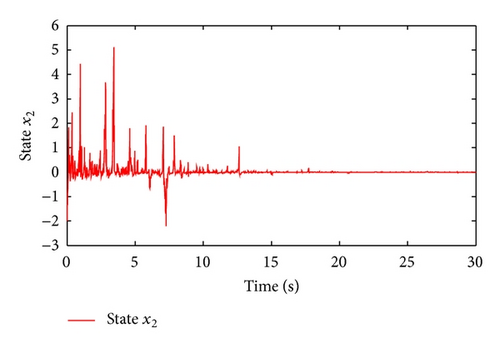
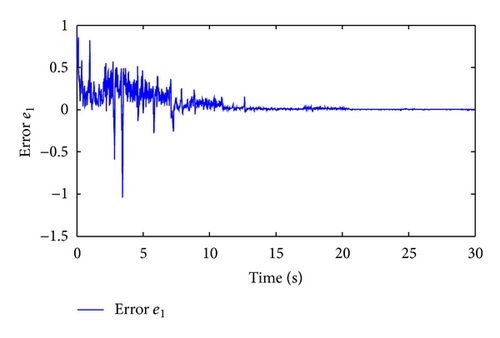
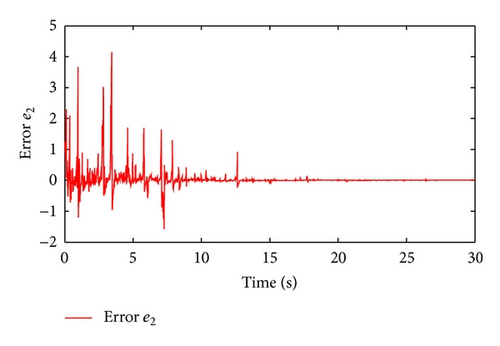
Figure 1 shows the switching signal of the switched system with the average dwell time T_α = 3. Figures 2 and 3 illustrate the state trajectories of the closed-loop system. The estimated errors are plotted in Figures 4 and 5, respectively. We can see from Figures 2–5 that the proposed observer can guarantee the convergence of the estimated error and the designed controller can guarantee the stability of the corresponding closed-loop system. This demonstrates the effectiveness of the proposed method.

In addition, some observer-based controller design approaches proposed in the existing literature [27–29] are only applicable to stochastic systems or Markovian jump systems and they cannot be used to stabilize the system considered in this section, which also shows the advantage of the proposed method.

5. Conclusions

In this paper, the problem of observer-based robust H_∞ stabilization for stochastic switched systems with time delay has been investigated. By using the average dwell time method, sufficient conditions which guarantee the mean-square exponential stability of switched stochastic systems with time delay are derived. Then, H_∞ performance analysis and observer-based H_∞ control for such systems are developed. Finally, a numerical example is given to demonstrate the effectiveness of the proposed approach.

Acknowledgment

This work was supported by the National Natural Science Foundation of China under Grant No. 61273120.

References

1 Lee T. C. and Jiang Z. P., Uniform asymptotic stability of nonlinear switched systems with an application to mobile robots, IEEE Transactions on Automatic Control. (2008) 53, no. 5, 1235–1252, https://doi.org/10.1109/TAC.2008.923688, MR2445677.
10.1109/TAC.2008.923688
Web of Science® Google Scholar
2 Zhang W.-A. and Yu L., New approach to stabilisation of networked control systems with time-varying delays, IET Control Theory & Applications. (2008) 2, no. 12, 1094–1104, https://doi.org/10.1049/iet-cta:20070291, MR2479004.
10.1049/iet-cta:20070291
Web of Science® Google Scholar
3 Donkers M. C. F., Heemels W. P. M. H., van de Wouw N., and Hetel L., Stability analysis of networked control systems using a switched linear systems approach, IEEE Transactions on Automatic Control. (2011) 56, no. 9, 2101–2115, https://doi.org/10.1109/TAC.2011.2107631, MR2865767.
10.1109/TAC.2011.2107631
Web of Science® Google Scholar
4 Narendra K. S. and Balakrishnan J., A common Lyapunov function for stable LTI systems with commuting A-matrices, IEEE Transactions on Automatic Control. (1994) 39, no. 12, 2469–2471, https://doi.org/10.1109/9.362846, MR1337573.
10.1109/9.362846
Web of Science® Google Scholar
5 Branicky M. S., Multiple Lyapunov functions and other analysis tools for switched and hybrid systems, IEEE Transactions on Automatic Control. (1998) 43, no. 4, 475–482, https://doi.org/10.1109/9.664150, MR1617575, ZBL0904.93036.
10.1109/9.664150
Web of Science® Google Scholar
6 Hespanha J. P. and Morse A. S., Stability of switched systems with average dwell-time, Proceedings of the 38th IEEE Conference on Decision and Control (CDC ′99), December 1999, 2655–2660, 2-s2.0-0033314314.
Google Scholar
7 Zhang L., Shi P., Wang C., and Gao H., Robust H_∞ filtering for switched linear discrete-time systems with polytopic uncertainties, International Journal of Adaptive Control and Signal Processing. (2006) 20, no. 6, 291–304, https://doi.org/10.1002/acs.901, MR2250329, ZBL1127.93324.
10.1002/acs.901
Web of Science® Google Scholar
8 Zhang L., Shi P., Boukas E.-K., and Wang C., H_∞ control of switched linear discrete-time systems with polytopic uncertainties, Optimal Control Applications & Methods. (2006) 27, no. 5, 273–291, https://doi.org/10.1002/oca.782, MR2265237.
10.1002/oca.782
Web of Science® Google Scholar
9 Zhang L., Shi P., and Boukas E.-K., H_∞ output-feedback control for switched linear discrete-time systems with time-varying delays, International Journal of Control. (2007) 80, no. 8, 1354–1365, https://doi.org/10.1080/00207170701377113, MR2354348, ZBL1133.93316.
10.1080/00207170701377113
Web of Science® Google Scholar
10 Zhang L., Shi P., Boukas E.-K., and Wang C., Robust l₂ − l_∞ filtering for switched linear discrete time-delay systems with polytopic uncertainties, IET Control Theory & Applications. (2007) 1, no. 3, 722–730, https://doi.org/10.1049/iet-cta:20060127, MR2334811.
10.1049/iet-cta:20060127
Web of Science® Google Scholar
11 Sun X.-M., Zhao J., and Hill D. J., Stability and L₂-gain analysis for switched delay systems: a delay-dependent method, Automatica. (2006) 42, no. 10, 1769–1774, https://doi.org/10.1016/j.automatica.2006.05.007, MR2249722.
10.1016/j.automatica.2006.05.007
Web of Science® Google Scholar
12 Sun Y. G., Wang L., and Xie G., Exponential stability of switched systems with interval time-varying delay, IET Control Theory & Applications. (2009) 3, no. 8, 1033–1040, https://doi.org/10.1049/iet-cta.2008.0162, MR2561157.
10.1049/iet-cta.2008.0162
Web of Science® Google Scholar
13 Wang R. and Zhao J., Exponential stability analysis for discrete-time switched linear systems with time-delay, International Journal of Innovative Computing, Information and Control. (2007) 3, no. 6 B, 1557–1564, 2-s2.0-54249169816.
Web of Science® Google Scholar
14 Xie D. and Wu Y., Stabilisation of time-delay switched systems with constrained switching signals and its applications in networked control systems, IET Control Theory & Applications. (2010) 4, no. 10, 2120–2128, https://doi.org/10.1049/iet-cta.2009.0016, MR2761441.
10.1049/iet-cta.2009.0016
Web of Science® Google Scholar
15 Xiang Z., Sun Y.-N., and Chen Q., Robust reliable stabilization of uncertain switched neutral systems with delayed switching, Applied Mathematics and Computation. (2011) 217, no. 23, 9835–9844, https://doi.org/10.1016/j.amc.2011.04.082, MR2811256, ZBL1227.34075.
10.1016/j.amc.2011.04.082
Web of Science® Google Scholar
16 Samuels J., On the mean square stability of random linear systems, IRE Transactions on Circuit Theory. (1959) 6, no. 5, 248–259.
10.1109/TCT.1959.1086608
Google Scholar
17 Xu S. and Chen T., Robust H_∞ control for uncertain stochastic systems with state delay, IEEE Transactions on Automatic Control. (2002) 47, no. 12, 2089–2094, https://doi.org/10.1109/TAC.2002.805670, MR1947734.
10.1109/TAC.2002.805670
Web of Science® Google Scholar
18 Xu S. and Chen T., H_∞ output feedback control for uncertain stochastic systems with time-varying delays, Automatica. (2004) 40, no. 12, 2091–2098, https://doi.org/10.1016/j.automatica.2004.06.018, MR2156154, ZBL1073.93022.
10.1016/j.automatica.2004.06.018
Web of Science® Google Scholar
19 Chen B.-S. and Zhang W., Stochastic H₂/H_∞ control with state-dependent noise, IEEE Transactions on Automatic Control. (2004) 49, no. 1, 45–57, https://doi.org/10.1109/TAC.2003.821400, MR2028541.
10.1109/TAC.2003.821400
Web of Science® Google Scholar
20 Chen W.-H., Guan Z.-H., and Lu X., Delay-dependent exponential stability of uncertain stochastic systems with multiple delays: an LMI approach, Systems & Control Letters. (2005) 54, no. 6, 547–555, https://doi.org/10.1016/j.sysconle.2004.10.005, MR2136874, ZBL1129.93547.
10.1016/j.sysconle.2004.10.005
Web of Science® Google Scholar
21 Feng W., Tian J., and Zhao P., Stability analysis of switched stochastic systems, Automatica. (2011) 47, no. 1, 148–157, https://doi.org/10.1016/j.automatica.2010.10.023, MR2878257, ZBL1209.93157.
10.1016/j.automatica.2010.10.023
Web of Science® Google Scholar
22 Xiang Z., Wang R., and Chen Q., Robust reliable stabilization of stochastic switched nonlinear systems under asynchronous switching, Applied Mathematics and Computation. (2011) 217, no. 19, 7725–7736, https://doi.org/10.1016/j.amc.2011.02.076, MR2799785, ZBL1232.93093.
10.1016/j.amc.2011.02.076
Web of Science® Google Scholar
23 Xiang Z., Qiao C., and Wang R., Robust H_∞ reliable control of uncertain stochastic switched non-linear systems, International Journal of Advance Mechatronic Systems. (2011) 3, no. 2, 98–108.
10.1504/IJAMECHS.2011.040681
Google Scholar
24 Liu J., Liu X., and Xie W.-C., Exponential stability of switched stochastic delay systems with non-linear uncertainties, International Journal of Systems Science. (2009) 40, no. 6, 637–648, https://doi.org/10.1080/00207720902755770, MR2541001.
10.1080/00207720902755770
Web of Science® Google Scholar
25 Chen Y. and Zheng W. X., On stability of switched time-delay systems subject to nonlinear stochastic perturbations, Proceedings of the 49th IEEE Conference on Decision and Control (CDC ′10), December 2010, 2644–2649, 2-s2.0-79953154233, https://doi.org/10.1109/CDC.2010.5717029.
10.1109/CDC.2010.5717029
Google Scholar
26 Xiang Z., Wang R., and Jiang B., Nonfragile observer for discrete-time switched nonlinear systems with time delay, Circuits, Systems, and Signal Processing. (2011) 30, no. 1, 73–87, https://doi.org/10.1007/s00034-010-9210-8, MR2769375, ZBL1205.94147.
10.1007/s00034-010-9210-8
Web of Science® Google Scholar
27 Abolmasoumi A. H. and Momeni H. R., Robust observer-based H_∞ control of a Markovian jump system with different delay and system modes, International Journal of Control, Automation and Systems. (2011) 9, no. 4, 768–776, 2-s2.0-80052661740, https://doi.org/10.1007/s12555-011-0419-5.
10.1007/s12555-011-0419-5
Web of Science® Google Scholar
28 Li L., Jia Y., Du J., and Yu F., Observer-based L₂−L_∞ control for a class of stochastic systems with time-varying delay, Proceedings of the 49th IEEE Conference on Decision and Control (CDC ′10), December 2010, 1023–1028, 2-s2.0-79953137079, https://doi.org/10.1109/CDC.2010.5717663.
10.1109/CDC.2010.5717663
Google Scholar
29 Chen G., Shen Y., and Zhu S., Non-fragile observer-based H_∞ control for neutral stochastic hybrid systems with time-varying delay, Neural Computing and Applications. (2011) 20, no. 8, 1149–1158, 2-s2.0-80054110669, https://doi.org/10.1007/s00521-010-0471-8.
10.1007/s00521-010-0471-8
Web of Science® Google Scholar
30 Zhai G., Hu B., Yasuda K., and Michel A. N., Disturbance attenuation properties of time-controlled switched systems, Journal of the Franklin Institute. (2001) 338, no. 7, 765–779, https://doi.org/10.1016/S0016-0032(01)00030-8, MR1867846, ZBL1022.93017.
10.1016/S0016-0032(01)00030-8
Web of Science® Google Scholar
31 Gu K., A further refinement of discretized Lyapunov functional method for the stability of time-delay systems, International Journal of Control. (2001) 74, no. 10, 967–976, https://doi.org/10.1080/00207170110047190, MR1847365, ZBL1015.93053.
10.1080/00207170110047190
Web of Science® Google Scholar
32 Xie L., Output feedback H_∞ control of systems with parameter uncertainty, International Journal of Control. (1996) 63, no. 4, 741–750, https://doi.org/10.1080/00207179608921866, MR1650819, ZBL0841.93014.
10.1080/00207179608921866
Web of Science® Google Scholar

All articles

Observer-Based Robust H_∞ Control for Switched Stochastic Systems with Time-Varying Delay

Abstract

1. Introduction

2. Problem Formulation and Preliminaries

3. Main Results

3.1. Stability Analysis

3.2. H_∞ Performance Analysis

3.3. Observer-Based Robust H_∞ Stabilization

4. Numerical Example

5. Conclusions

Acknowledgment

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Observer-Based Robust H∞ Control for Switched Stochastic Systems with Time-Varying Delay

Abstract

1. Introduction

2. Problem Formulation and Preliminaries

3. Main Results

3.1. Stability Analysis

3.2. H∞ Performance Analysis

3.3. Observer-Based Robust H∞ Stabilization

4. Numerical Example

5. Conclusions

Acknowledgment

References

Figures

References

Related

Information

Observer-Based Robust H_∞ Control for Switched Stochastic Systems with Time-Varying Delay

3.2. H_∞ Performance Analysis

3.3. Observer-Based Robust H_∞ Stabilization