Journal of Computational Methods in Physics
Volume 2013, Issue 1 308538
Research Article
Open Access

Dynamics Underlying the Gaussian Distribution of the Classical Harmonic Oscillator in Zero-Point Radiation

Wayne Cheng-Wei Huang, 

Corresponding Author

Wayne Cheng-Wei Huang

Department of Physics and Astronomy, University of Nebraska-Lincoln, Lincoln, NE 68588, USA unl.edu

Search for more papers by this author
Herman Batelaan, 

Herman Batelaan

Department of Physics and Astronomy, University of Nebraska-Lincoln, Lincoln, NE 68588, USA unl.edu

Search for more papers by this author
First published: 07 October 2013
https://doi.org/10.1155/2013/308538
Citations: 8
Academic Editor: Marta B. Rosales

Abstract

Stochastic electrodynamics (SED) predicts a Gaussian probability distribution for a classical harmonic oscillator in the vacuum field. This probability distribution is identical to that of the ground state quantum harmonic oscillator. Thus, the Heisenberg minimum uncertainty relation is recovered in SED. To understand the dynamics that give rise to the uncertainty relation and the Gaussian probability distribution, we perform a numerical simulation and follow the motion of the oscillator. The dynamical information obtained through the simulation provides insight to the connection between the classic double-peak probability distribution and the Gaussian probability distribution. A main objective for SED research is to establish to what extent the results of quantum mechanics can be obtained. The present simulation method can be applied to other physical systems, and it may assist in evaluating the validity range of SED.

1. Introduction

According to quantum electrodynamics, the vacuum is not a tranquil place. A background electromagnetic field, called the electromagnetic vacuum field, is always present, independent of any external electromagnetic source [1]. The first experimental evidence of the vacuum field dates back to 1947 when Lamb and his student Retherford found an unexpected shift in the hydrogen fine structure spectrum [2, 3]. The physical existence of the vacuum field has inspired an interesting modification to the classical mechanics, known as stochastic electrodynamics (SED) [4]. As a variation of classical electrodynamics, SED adds a background electromagnetic vacuum field to the classical mechanics. The vacuum field as formulated in SED has no adjustable parameters except that each field mode has a random initial phase and the field strength is set by the Planck constant, ℏ. With the aid of this background field, SED is able to reproduce a number of results that were originally thought to be pure quantum effects [1, 4–8].

Despite that the classical mechanics and SED are both theories that give trajectories of particles, the probability distributions of the harmonic oscillator in both theories are very different. In a study of the harmonic oscillator, Boyer showed that the moments 〈xn〉 of an SED harmonic oscillator are identical to those of the ground state quantum harmonic oscillator [9]. As a consequence, the Heisenberg minimum uncertainty relation is satisfied, and the probability distributions of an SED harmonic oscillator are a Gaussian, identical to that of the ground state quantum harmonic oscillator. While in classical mechanics it is most likely to find an oscillator at the two turning points of the trajectory, hence the double-peak probability distribution, the SED Gaussian probability distribution has the maximum in the center (see Figure 1). How do the dynamics differ in the two classical theories so that the probability distributions become so different?

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
A comparison between the harmonic oscillators with and without the vacuum field. Top: without any external force except for the vacuum field, the SED harmonic oscillator undergoes a motion that results in a Gaussian probability distribution. This motion is investigated with our simulation. Bottom: in the absence of the vacuum field or any external drive, a harmonic oscillator that is initially displaced from equilibrium performs a simple harmonic oscillation with constant oscillation amplitude. The resulting probability distribution has peaks at the two turning points.

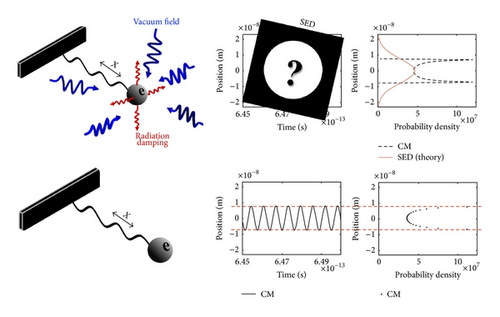
Although the analytical solution of an SED harmonic oscillator was given a long time ago, it is not straightforward to see the dynamical properties of a single particle from the complicated solution. Additionally, many results in SED such as probability distribution are obtained from (ensemble) phase averaging. Thus, they cannot be used for the interpretation of a single particle’s dynamical behavior in time (some may consider applying the central limit theorem and treat the positions in the time sequence as independent random variables. However, for an SED system this cannot work, because the correlation between the motion at two points in time persists beyond many cycles of oscillation) unless the system is proved to be ergodic. As an analytical proof of the ergodicity is very difficult, we take a numerical approach to study the particle’s dynamical behavior. Besides what is already known from the analytical solution, our numerical studies construct the probability distribution from a single particle’s trajectory. We investigate the relation between such a probability distribution and the particle’s dynamical behavior. Ultimately, we want to know the underlying mechanism that turns the classic double-peak distribution into the Gaussian distribution.

While most works in the field of SED are analytical, numerical studies are rare [10–12]. The advantage of numerical simulation is that it may be extended to other physical systems with relative ease and is flexible in testing different assumptions and approximations. For example, in most SED analyses the effect of the Lorentz force due to the vacuum field is often neglected as the first-order approximation [5]. However, when the field gradient is nonzero, the Lorentz force from the magnetic field can work with the electric field to give a nonzero drift to a charged particle, known as the ponderomotive force. Therefore, the Lorentz force of the vacuum field may play a significant role in SED. In fact, it is shown in the literature that the magnetic part of the vacuum field is responsible for the self-ionization of the atoms and the acquisition of an energy 1020 eV in a few nanoseconds by part of a free electron in vacuum [13, 14]. Using numerical simulation, one can easily examine SED beyond the first-order approximation (in this work we limit ourselves to physical parameters where we expect the Lorentz force effects to be minimal, as this work is compared to analytical results where this approximation is made), and the Lorentz force effects in SED can be investigated.

The major challenge for the numerical simulation is to properly account for the vacuum field modes. A representative sampling of the modes is thus the key for successful simulations. In this study, one of our goals is to use a simple physical system, namely, the simple harmonic oscillator, to benchmark our numerical method of vacuum mode selection so that it can be used to test the validity range of SED as discussed in the following.

Over the decades, SED has been criticized for several drawbacks [15]. Authors like Cavalleri argued that SED can neither explain electron slit-diffraction nor derive the nonlinear Schrödinger equation; moreover, SED implies broad radiation and absorption spectra for rarefied gases. In the case of the quartic anharmonic oscillator, Pesquera and Claverie showed that SED disagrees with quantum mechanics [16]. Additionally, the results claimed in [17–19] were shown to be wrong due to improper relativistic approximation [20]. While these theoretical analyses are documented in detail, it may be useful to use numerical simulation as an independent check in order to establish the validity range of SED, which is one of the objectives of our work.

Meanwhile, a modified theory called stochastic electrodynamics with spin (SEDS) was recently proposed [15]. As SEDS are an extension of SED with a model of electron spin motion, it is argued that the introduction of electron spin can eliminate several drawbacks of SED. Among all, it is claimed that SEDS allows the derivation of the complete and even the generalized Schrödinger equation [21–24]. Also, it is claimed that SEDS can explain electron slit-diffraction and the sharp spectral lines of the rarefied gases [25]. In view of the fact that SEDS is a modified theory from SED and may extend its validity range, it is probably important as a next step to apply numerical simulation to such a model as a “quasi-experiment” and test some of its claims. Models that include constraints can be incorporated in our numerical model with, for example, Lagrange multipliers.

The organization of this paper is the following. First, in Section 2 Boyer’s results on the SED harmonic oscillator are briefly reviewed. Based on these results, the probability distribution for the oscillator is derived. Second, in Section 3 details for simulating the vacuum field and the SED harmonic oscillator are documented. Third, in Section 4 the trajectory of the SED harmonic oscillator is solved numerically, and the constructed probability distribution is compared to the analytical probability distribution. Two sampling methods are used in constructing the probability distribution from the simulated trajectories. The first method is “sequential sampling,” which is suitable for studying the relation between the dynamics of the SED harmonic oscillator and its probability distribution. The second approach is “ensemble sampling,” which lends itself well to parallel computing and is convenient for statistical interpretations. Lastly, in Section 6 we discuss some potential applications of the numerical simulation in studying other quantum phenomena. Numerical studies have an advantage over the analytical solutions in that they can be adopted to a range of physical systems, and we hope that the current method of simulation may also assist in assessing SED’s validity range.

2. Theory of Stochastic Electrodynamics

2.1. Brief Review of Boyer’s Work

In his 1975 papers [4, 9], Boyer calculated the statistical features of an SED harmonic oscillator, and the Heisenberg minimum uncertainty relation is shown to be satisfied for such an oscillator. The vacuum field used in Boyer’s work arises from the homogeneous solution of Maxwell’s equations, which is assumed to be zero in classical electrodynamics [4]. In an unbounded (free) space, the vacuum field has an integral form (a detailed account of the vacuum field in unbounded space is given in Appendix A.1) [26]:
()
()
where ω = c|k|, and is the random phase uniformly distributed in [0,2π]. The integral is to be taken over all k-space. The two unit vectors, ε(k, 1) and ε(k, 2), describe a polarization basis in a plane that is perpendicular to the wave vector k:
()
Furthermore, the polarization basis vectors are chosen to be mutually orthogonal:
()
To investigate the dynamics of the SED harmonic oscillator, Boyer used the dipole approximation,
()
to remove the spatial dependence in the vacuum field (1). Therefore, the equation of motion for an SED harmonic oscillator used in Boyer’s analysis is
()
where Γ ≡ (2q2/3mc3)(1/4πϵ0) is the radiation damping parameter, m is the mass, q is the charge, and ω0 is the natural frequency. The x-component of the vacuum field in (6) is
()
and the steady-state solution is obtained as
()
where . Additionally, using the condition of sharp resonance,
()
Boyer further calculated the standard deviation of position and momentum from (8) by averaging over the random phase [9]:
()
()
where the phase averaging represents the ensemble average over many realizations. In each realization, the random phase of the vacuum field is different. The above result satisfies the Heisenberg minimum uncertainty relation:
()
From an energy argument, Boyer showed that this uncertainty relation can also be derived from a delicate balance between the energy gain from the vacuum field and the energy loss through radiation damping [4].

2.2. Probability Distribution

Given the knowledge of the moments , the Fourier coefficients of the probability distribution can be determined by Taylor expanding e−ikx in powers of xn:
()
Using (8) and the relation from Boyer’s paper [9]
()
the moments can be evaluated:
()
where m is a natural number. Consequently, only even-power terms are contributing in (13), and the Fourier coefficients can be determined:
()
Therefore, although not explicitly given, it is implied by Boyer’s work [9] that the probability distribution of the SED harmonic oscillator is
()
which is identical to the probability distribution of the quantum harmonic oscillator in the ground state (this result is consistent with the phase space probability distribution given in Marshall’s work [27]).

3. Methods of Numerical Simulation

3.1. Vacuum Field in Bounded Space

While the vacuum field in unbounded space is not subject to any boundary condition and thus every wave vector k is allowed [4], the field confined in a space of volume V with zero value boundary condition has a discrete spectrum, and a summation over infinitely many countable wave vectors k is required [1]. In a simulation, it is convenient to write the vacuum field in the summation form:
()
where , ω = c|k|, is the random phase uniformly distributed in [0,2π], and V is the volume of the bounded space. A derivation of the summation form of the vacuum field in bounded space is given in Appendix A.2.
Since the range of the allowed wave vectors k is over the whole k-space, we choose to sample only the wave vectors k whose frequencies are within the finite range [ω0 − Δ/2, ω0 + Δ/2]. Such sampling is valid as long as the chosen frequency range Δ completely covers the characteristic resonance width of the harmonic oscillator:
()
On the other hand, the distribution of the allowed wave vectors k depends on the specific shape of the bounded space. In a cubic space of volume V, the allowed wave vectors k are uniformly distributed at cubic grid points, and the corresponding vacuum field is
()
The sampling density is uniform and has a simple relation with the space volume V:
()
Nevertheless, such uniform cubic sampling is not convenient for describing a frequency spectrum, and it requires a large number of sampled modes to reach numerical convergence. In order to sample only the wave vectors k in the resonance region, spherical coordinates are used. For the sampling to be uniform, each sampled wave vector k must occupy the same size of finite discrete volume element Δ3k = k2sinθΔkΔθΔϕ. To sample for modes in the resonance region with each mode occupying the same volume size, we use a set of specifically chosen numbers (κijn, ϑijn, φijn) to sample the wave vectors k. For i = 1, …, Nκ, j = 1, …, Nϑ, and n = 1, …, Nφ,
()
where is a random number uniformly distributed in [0,2π], and the stepsizes are constant:
()
()
The random number is used here to make the sampling more efficient. A set of numbers (κijn, ϑijn, φijn) is then used for assigning the spherical coordinates to each sampled wave vector k:
()
where
()
Therefore, each sampled wave vector kijn is in the resonance region and occupies the same size of finite discrete volume element:
()
where the differential equalities dϑ = sinθ dθ, dκ = k2dk, and dφ = dϕ are used. The differential limit is reached when Nκ, Nϑ, and Nφ are sufficiently large. The numerical result converges to the analytical solution in this limit. Under the uniform spherical sampling method (described by (22), (25), and (26)), the expression for the vacuum field, (18), becomes
()
where k = kijn. It is worth noting that when the total number of wave vectors Nk becomes very large, both uniform spherical and cubic sampling converge to each other because they both effectively sample all the wave vectors k in k-space. In the limit of large sampling number Nk → ∞, the two sampling methods are equivalent (the relation ρk = 1/Δ3k = Nk/Vk = V/(2π) 3 implies that the limit of large sampling number (i.e., Nk → ∞) is equivalent to the limit of unbounded space (i.e., V → ∞). At this limit, the volume element becomes differential (denoted as d3k) and is free from any specific shape associated with the space boundary. Therefore, all sampling methods for the allowed wave vectors k become equivalent, and the summation approaches the integral. This is consistent with the fact that no volume factor V is involved in the vacuum field integral, as shown in (1)), and (21) can be used for both sampling methods to calculate the volume factor V in (20) and (28):
()
where
()
In the simulation, the summation indices in (28) can be rewritten as
()
where the multiple sums indicate a numerical nested loop and the wave vector k = kijn is chosen according to the uniform spherical sampling method. To achieve numerical convergence, Nϑ and Nφ need to be sufficiently large so that the wave vector k at a fixed frequency may be sampled isotropically. In addition, a large Nκ is required for representative samplings in frequency. As a result, Nk = NκNϑNφ needs to be very large when using uniform spherical sampling for numerical simulation. To improve the efficiency of the computer simulation, we sample k at one random angle (θi, ϕi) for each frequency. Namely, for i = 1, …, Nω,
()
where
()
()
The stepsize Δκ is specified in (23), is a random number uniformly distributed in [−1,1], and is another random number uniformly distributed in [0,2π]. As the number of sampled frequencies Nω becomes sufficiently large, the random angles (θi, ϕi) will approach the angles specified in uniform spherical sampling (22).
In the limit of Δ/ω0 ≪ 1, the above sampling method (described by (32), (33), and (34)) and the uniform spherical sampling method both approach a uniform sampling on a spherical surface at the radius rk = ω0/c. In this limit, the addition of the condition in (19) leads to the possible choices for the frequency range Δ:
()
Within this range (35), the expression for the vacuum field in (18) becomes
()
where k = ki. For large Nk = Nω, the volume factor V is calculated using (29).
Finally, for a complete specification of the vacuum field, (36), the polarizations εk,λ need to be chosen. From (29), we notice that large Nk gives large V. Since for large V the vacuum field is not affected by the space boundary, there should be no preferential polarization direction and the polarizations should be isotropically distributed. The construction for isotropically distributed polarizations is discussed in detail in Appendix B. Here we give the result that satisfies the property of isotropy and the properties of polarization (described by (3) and (4)):
()
where χ is a random number uniformly distributed in [0,2π]. With the wave vectors k (described by (32), (33), and (34)) and the polarizations εk,λ (described by (37)), the endpoints of the sampled vacuum field vector are plotted on a unit sphere, as shown in Figure 2, which illustrates the isotropy of the distribution.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The isotropic distribution of the polarization field vectors εk,1 (number of sampled frequencies number Nω = 3 × 103). The endpoints of the polarization field vectors, εk,1, are plotted for a random sampling of modes (k, 1) according to the methods described in (32), (33), and (34).

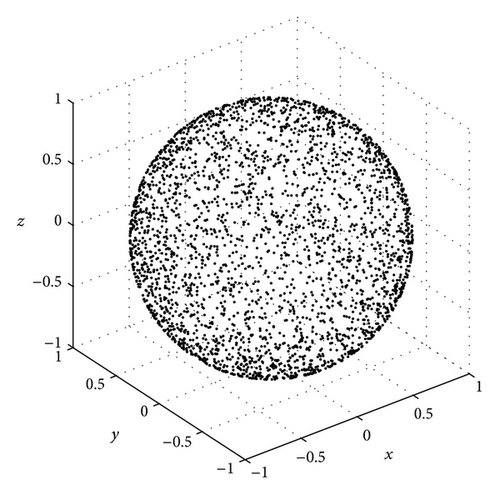
In summary, the vacuum field mode (k, λ) in (36) can be sampled by a set of four numbers (κi, ϑi, φi, χi), which are specified in (32), (33), (34), and (37). The only assumption used in determining these numbers is (35), which is equivalent to the sharp resonance condition (9) used in Boyer’s analysis.

3.2. Equation of Motion in Numerical Simulation

In the unbounded (free) space, the equation of motion in Boyer’s analysis is
()
where the dipole approximation k · r ≪ 1 (5) is used. In the bounded space, the equation of motion remains the same, but the vacuum field formulated has the summation form (36):
()
where . The steady-state solution to (38) in the bounded space can be found following Boyer’s approach:
()
where . While this analytical solution can be evaluated using our method of vacuum mode selection ((32), (33), (34), and (37)), our goal with the numerical simulation is to first reproduce Boyer’s analytical results (8) and then later extend the methods to other physical systems. One major obstacle for the numerical approach is the third-order derivative in the radiation damping term, . To circumvent this problem, we follow the perturbative approach in [28–30]. According to classical electrodynamics, the equation of motion for an electron with radiation damping is
()
where F is the force and Γ ≡ (2e2/3mc3)(1/4πϵ0) is the radiation damping coefficient. Under the assumption , the zero-order equation of motion is
()
The justification for the assumption is that a point particle description of the electron is used in classical electrodynamics [28, 30]. Using (42), the radiation damping term may be estimated by
()
which can be iterated back to the original equation (41) and get a perturbative expansion:
()
Thus, in this approximated equation of motion we replace the third derivative of position x by the first derivative of the force F. Applying (44) to (38), the equation of motion becomes
()
The order of magnitude for each term on the right-hand side is
()
()
()
()
where x0 and E0 are the order of magnitude for the particle motion x and the vacuum field Evac,x. The order of magnitude for the time scale of particle motion is given by 1/ω0 because of the sharp resonance condition (9). In order to compare the two radiation damping terms ((48) and (49)), we use a random walk model to estimate x0 and E0. For a fixed time t = t0, the order of magnitude for Evac,x(t0) and x(t0) (see (39) and (40)) is equal to E0 and x0. Written as complex numbers, the mathematical form of and is analogous to a two-dimensional random walk on the complex plane with random variable Θ{k,λ}, where {k, λ} denotes a set of modes (k, λ). Averaging over {k, λ}, the order of magnitude for Evac,x(t0) and x(t0) can be estimated by the root-mean-squared distance of and . In a two-dimensional random walk model [31], the root-mean-squared distance Drms is given by
()
where Ns is the number of steps taken and Δs is a typical stepsize; for ,  , and for ,  . Hence, the order of magnitude, E0 and x0, may be estimated as (using V = (2π)3Nω/Vk and ((29) and (30)), the value of x0 in (51) can be estimated as , which is consistent with Boyer’s calculation for the standard deviation of position in (10))
()
The order of magnitude for the two radiation damping terms is evaluated accordingly:
()
Using the sharp resonance condition Γω0 ≪ 1 (9), we approximate the equation of motion (45) to its leading order:
()
As an additional note, given the estimation of E0 and x0 in (51), the three force terms in (53) have the following relation:
()
Thus, the linear restoring force is the dominating drive for an SED harmonic oscillator, while the vacuum field qEvac,x and radiation damping act as perturbations. The balance between the vacuum field and the radiation damping constrains the oscillation amplitude to fluctuate in the vicinity of x0.
Finally, as we have established an approximated equation of motion (53) for numerical simulation, the total integration time τint  (i.e., how long the simulation is set to run) needs to be specified. Upon inspection, two important time scales are identified from the analytical solution of (53):
()
where A is a coefficient determined by the initial conditions and
()
The first term in (55) represents the transient motion and the second term represents the steady-state motion. The characteristic time for the transient motion is
()
Thus, the simulation should run beyond τtran  if one is interested in the steady-state motion. As the steady-state solution is a finite discrete sum of periodic functions, it would have a nonphysical repetition time τrep. The choice of τint  should satisfy τint  ≤ τrep to avoid repetitive solutions. A detailed discussion about τrep can be found in Appendix C. Here we give a choice of τint ,
()
where Δω is the frequency gap and it can be estimated using (23), (33), and (34),
()
where .

To summarize, (53) is the approximated equation of motion to be used in numerical simulation. The vacuum field Evac,x in (53) is given by (39). The specifications of the vacuum field modes (k, λ), polarizations εk,λ, and other relevant variables can be found in Section 3.1. To approximate (38) by (53), two conditions need to be used, namely, the dipole approximation (5) and the sharp resonance condition (9). The parameters q, m, and ω0 simulation should be chosen to satisfy these two conditions, as these two conditions are also used in Boyer’s analysis. Lastly, the integration time τint  for the simulation is chosen to be within the range τtrans  ≪ τint  ≤ τrep, where τtran  and τrep are given in (57) and (58), respectively.

4. Simulation Results

In Section 2, it was shown that the probability distribution for an SED harmonic oscillator is a Gaussian. In Section 3, we develop the methods for a numerical simulation to investigate the dynamics of the SED harmonic oscillator and how it gives rise to the Gaussian probability distribution. In this section, the results of the simulation are presented, and the relation between the trajectory and the probability distribution is discussed.

To construct the probability distribution from a particle’s trajectory, two sampling methods are used. The first method is sequential sampling and the second method is ensemble sampling. In sequential sampling the position or velocity is recorded in a time sequence from a single particle’s trajectory, while in ensemble sampling the same is recorded only at the end of the simulation from an ensemble of particle trajectories. The recorded positions or velocities are collected in histogram and then converted to a probability distribution for comparison to the analytical result (17). Whereas the sequential sampling illustrates the relationship between the buildup of probability distribution and the dynamics of particle trajectory, the ensemble sampling is convenient for statistical interpretation. In addition, the ensemble sampling is suitable for parallel computing, which can be used to improve the computation efficiency.

4.1. Particle Trajectory and the Probability Distribution

By solving (53) numerically, the steady-state trajectory for the SED harmonic oscillator is obtained and shown in Figure 3. For a comparison, the temporal evolution of the vacuum field (39) is also included. The ordinary differential equation (53) is solved using the adaptive 5th order Cash-Karp Runge-Kutta method [32], and the integration stepsize is set as small as one-twentieth of the natural period, (1/20)(2π/ω0), to avoid numerical aliasing. The charge q, mass m, natural frequency ω0, and vacuum field frequency range Δ are chosen to be
()
where e is the electron charge, me is the electron mass, and is the resonance width of the harmonic oscillator. The choice of m = 10−4me is made to bring the modulation time and the natural period of the harmonic oscillator closer to each other. In other words, the equation of motion (53) covers time scales at two extremes, and the choice of mass m = 10−4me brings these two scales closer so that the integration time is manageable without losing the physical characteristics of the problem.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
A comparison between particle trajectory and the temporal evolution of the vacuum field. Top: the vacuum field (red) is compared to the trajectory of the SED harmonic oscillator (black). Bottom: a magnified section of the trajectory shows that there is no fixed phase or amplitude relation between the particle trajectory and the instantaneous driving field. The modulation time for the field is also shown to be longer than that for the motion of the harmonic oscillator.
Here we would like to highlight some interesting features of the simulated trajectory (Figure 3). First, there appears to be no fixed phase or amplitude relation between the particle trajectory and the instantaneous driving field. Second, the rate of amplitude modulation in the particle trajectory is slower than that in the driving field. To gain insights into these dynamical behaviors, we study the steady-state solution of (55) in the Green function form [33]:
()
where . The solution indicates that the effect of the driving field Evac,x(t′) at any given time t′ lasts for a time period of beyond t′. In other words, the particle motion x(t) at time t is affected by the vacuum field Evac,x(t′) from all the previous moments (t′ ≤ t). As the vacuum field fluctuates in time, the fields at two points in time only become uncorrelated when the time separation is much longer than one coherence time (the coherence time of the vacuum field is , see (64)). This property of the vacuum field reflects on the particle trajectory, and it explains why the particle trajectory has no fixed phase or amplitude relation with the instantaneous driving field. Another implication of (61) is that it takes a characteristic time for the particle to dissipate the energy gained from the instantaneous driving field. Thus, even if the field already changes its amplitude, it would still take a while for the particle to follow. This explains why the amplitude modulation in the particle trajectory is slower compared to that in the driving field (however, in case of slow field modulation when the field bandwidth is shorter than the resonance width of the harmonic oscillator, the modulation time of the field and the particle trajectory are the same).

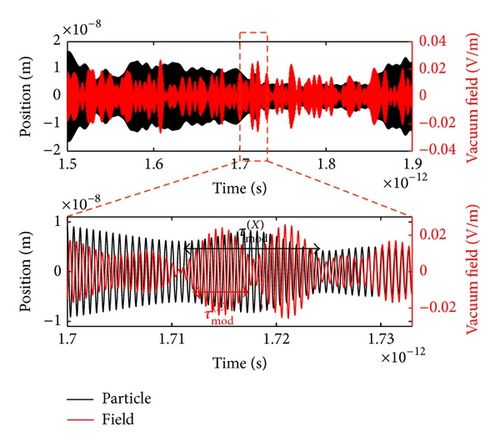
The sequential sampling of a simulated trajectory gives the probability distributions in Figure 4. While Boyer’s result is obtained through ensemble (phase) averaging, the Gaussian probability distribution shown here is constructed from a single trajectory and is identical to the probability distribution of a ground state quantum harmonic oscillator.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The probability distribution constructed from a single particle’s trajectory (number of sampled frequencies Nω = 2   ×   104). Left: the position and momentum probability distributions for the SED harmonic oscillator (black dot) and the ground state quantum harmonic oscillator (red and blue lines) are compared. Right: an illustration of the sequential sampling shows how positions are recorded at a regular time sequence (red cross). Note that at small time scale the oscillation amplitude is constant, but at large time scale it modulates.
To understand how the trajectory gives rise to a Gaussian probability distribution, we investigate the particle dynamics at two time scales. At short time scale, the particle oscillates in a harmonic motion. The oscillation amplitude is constant, and the period is T = 2π/ω0. Such an oscillation makes a classical double-peak probability distribution. At large time scale, the oscillation amplitude modulates. As a result, different parts of the trajectory have double-peak probability distributions associated with different oscillation amplitudes, which add to make the final probability distribution a Gaussian distribution, as shown in Figure 5. To verify this idea, we attempt to reconstruct the Gaussian probability distribution from the double-peak probability distributions at different sections of the trajectory. We approach this problem by numerically sampling the oscillation amplitudes at a fixed time-step. To determine the appropriate sampling time-step, we inspect the steady-state solution (55) in its complex form:
()
Since the frequency components can be sampled symmetrically around ω0, we factorize into an amplitude term A(t) and an oscillation term :
()
The complex components rotate in the complex plane at different rates ω − ω0. At any given time, the configuration of these components determines the magnitude of A(t), as shown in Figure 6. As time elapses, the configuration evolves and the amplitude A(t) changes with time. When the elapsed time Δt is much shorter than the shortest rotating period , the change in the amplitude A(t) is negligible:
()
where . Here we denote this shortest rotating period as coherence time (the coherence time τcoh as defined here is equivalent to the temporal width of the first-order correlation function (autocorrelation). As the autocorrelation of the simulated trajectory is the Fourier transform of the spectrum according to Wiener-Khinchin theorem, it has a temporal width the same as the coherence time τcoh calculated here) τcoh. For our problem at hand, it is clear that the sampling of oscillation amplitudes should use a time-step greater than τcoh.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Contributions of different oscillation amplitudes in the final probability distribution. Top: several sections (red) of a steady-state trajectory (black) are shown. A section is limited to the duration of the characteristic modulation time. The oscillation amplitude changes significantly beyond the characteristic modulation time, so different sections of the trajectory obtain different oscillation amplitudes. Bottom: the probability distributions of each section of the trajectory are shown. As the oscillation amplitude is approximately constant in each section, the corresponding probability distribution (red bar) is close to the classic double-peak distribution. The probability distributions in different sections of the trajectory contribute to different areas of the final probability distribution (black dashed line). The final probability distribution is constructed from the steady-state trajectory.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
A schematic illustration of the oscillation amplitude as a sum of different frequency components in the complex plane. At a particular time t = t0, an oscillation amplitude A(t0) (blue solid arrow) is formed by a group of frequency components (blue dashed arrow), which rotate in the complex plane at different rates. After a time Δt ≪ τcoh, the angles of the frequency components (red dashed arrow) change only a little. Therefore, the oscillation amplitude A(t0 + Δt) (red solid arrow) does not change much within the coherence time.
A representative sampling of the oscillation amplitudes with each sampled amplitude separated by 3τcoh is shown in Figure 7. In this figure, the histogram of the sampled oscillation amplitudes shows that the occurrence of large or small amplitudes is rare. Most of the sampled amplitudes have a medium value. This is because the occurrence of extreme values requires complete alignment or misalignment of the complex components in A(t). For most of the time, the complex components are in partial alignment and thus give a medium value of A(t). Interestingly, the averaged value of A(t) is close to the oscillation amplitude x0 as predicted by the random walk model (51). Using the amplitude distribution given in Figure 7, a probability distribution can be constructed by adding up the double-peak probability distributions:
()
where A is oscillation amplitude, f(A) is the amplitude distribution, and PA(x) is the corresponding double-peak probability distribution. This constructed probability distribution is a Gaussian and is identical to the simulation result shown in Figure 4. The reconstruction of the Gaussian probability distribution indicates the transitioning from double-peak distribution to the Gaussian distribution due to the amplitude modulation driven by the vacuum field.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Sampled oscillation amplitude and the reconstructed Gaussian probability distribution. Top: the oscillation amplitudes (red dot) are sampled from a steady-state trajectory (black) with a sampling time-step equal to 3τcoh, where τcoh is the coherence time. Middle: a magnified section of the trajectory shows that the sampling time-step (red dot) is 3τcoh. Bottom: using the amplitude distribution (red bar), a probability distribution (blue line) is constructed and shown to agree with the simulated Gaussian probability distribution (black dot). The simulated probability distribution (black dot) is offset by Δs = 1.5   ×   107 for better visualization. This result confirms that the underlying mechanism for the Gaussian probability distribution is the addition of a series of double-peak probability distributions according to the amplitude distribution given by the vacuum field. It is also worth noting that the most frequent oscillation amplitude in the amplitude distribution is at the half-maximum of the position distribution (black dot).

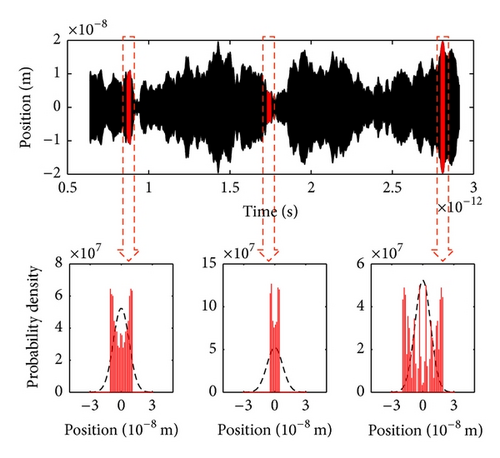
4.2. Phase Averaging and Ensemble Sampling

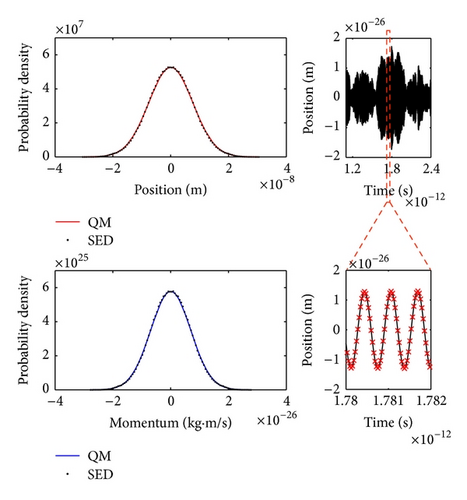
In many SED analyses [4–7, 9, 34], the procedure of random phase averaging is often used to obtain the statistical properties of the physical system. A proper comparison between numerical simulation and analysis should thus be based on ensemble sampling. In each realization of ensemble sampling, the particle is prepared with identical initial conditions, but the vacuum field differs in its initial random phase . The difference in the initial random phase corresponds to the different physical realizations in random phase averaging. At the end of the simulation, physical quantities such as position and momentum are recorded from an ensemble of trajectories.

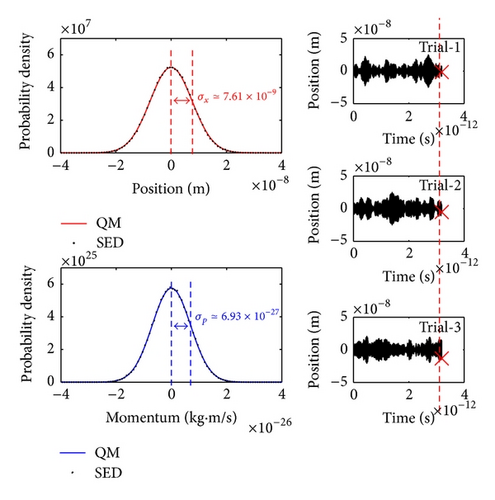
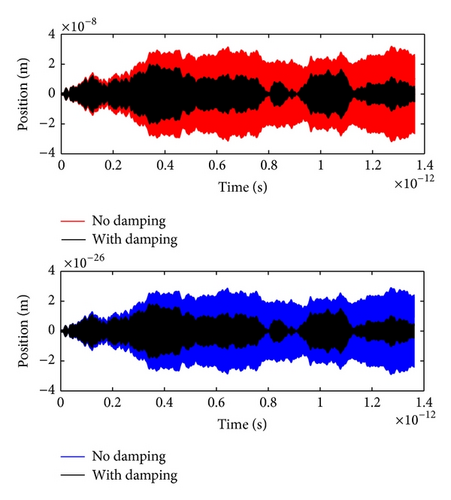
The ensemble sampling of the simulation gives the probability distributions in Figure 8. The position and momentum distributions satisfy the Heisenberg minimum uncertainty as predicted by Boyer’s analysis. In addition, Boyer proposed a mechanism for the minimum uncertainty using an energy-balance argument. Namely, he calculated the energy gain from the vacuum field and the energy loss through radiation damping, and he found that the delicate balance results in the minimum uncertainty relation [4]. We confirm this balancing mechanism by turning off the radiation damping in the simulation and see that the minimum uncertainty relation no longer holds (see Figure 9).

Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
The probability distribution constructed from an ensemble sampling (number of particles Np = 2   ×   105, number of sampled frequencies  Nω = 2   ×   103). Left: the position and momentum probability distributions are shown for the SED harmonic oscillator (black dot) and the ground state quantum harmonic oscillator (red and blue line). The ensemble sampling corresponds to the procedure of random phase averaging ((10) and (11)), so the width of the probability distributions should satisfy Heisenberg’s minimum uncertainty relation (σxσp = ℏ/2) as predicted by the analysis. Right: an illustration of the ensemble sampling shows how positions (red cross) are recorded from an ensemble of trajectories (black line).
Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
Radiation damping and Heisenberg’s minimum uncertainty relation. Under the balance between vacuum field driving and the radiation damping, the trajectory of the SED harmonic oscillator (black) satisfies the Heisenberg minimum uncertainty relation. When the radiation damping is turned off in the simulation (red and blue), the minimum uncertainty relation no longer holds, although the range of the particle’s motion is still bounded by the harmonic potential.

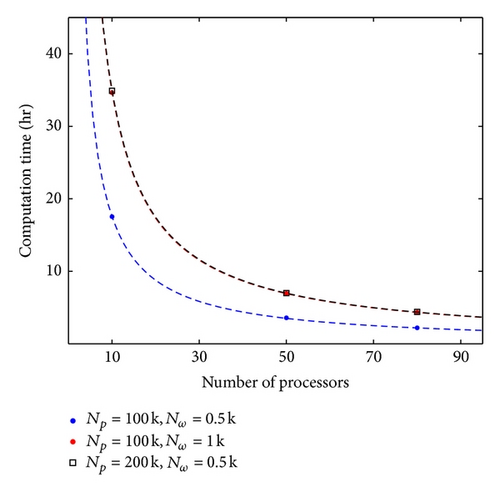
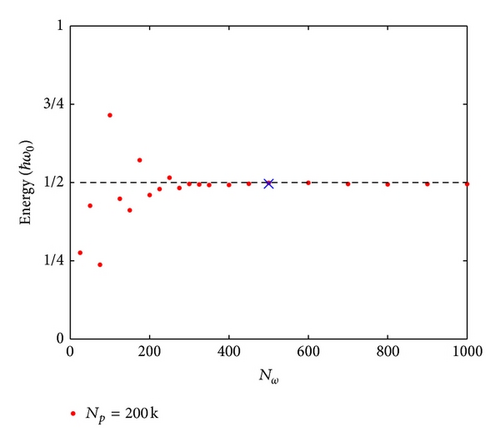
Unlike sequential sampling, ensemble sampling has the advantage that the recorded data are fully uncorrelated. As a result, the integration time does not need to be very long compared to the coherence time τcoh. However, since only one data point is recorded from each trajectory, a simulation with ensemble sampling actually takes longer time than with sequential sampling. For example, a typical simulation run with sequential sampling takes 2.3 hours to finish (for number of sampled frequencies Nω = 2   ×   104), but with ensemble sampling it takes 61 hours (for number of particles Np = 2   ×   105 and number of sampled frequencies Nω = 5   ×   102). A remedy to this problem is to use parallel computing for the simulation. The parallelization scheme (the parallelization of the simulation program is developed and benchmarked with assistance from the University of Nebraska, Holland Computing Center. The program is written in Fortran and parallelized using message passing interface (MPI) [32, 35]. The compiler used in this work is the GNU Compiler Collection (GCC) gcc-4.4.1 and the MPI wrapper used is openmpi-1.4.3.) for our simulation with ensemble sampling is straightforward, since each trajectory is independent except for the random initial phases . To reduce the amount of interprocessor communication and computation overhead, each processor is assigned an equal amount of work. The parallelized program is benchmarked and shows an inverse relation between the computation time and the number of processors (see Figure 10). As the computation speedup is defined as Sp = T1/Tp, where T1 is the single processor computation time and Tp is the multiprocessor computation time, the inverse relation shown in Figure 10 indicates ideal performance of linear speedup. As an additional note, the parallelized code is advantageous for testing the numerical convergence of the simulation. In Figure 11, the convergence of the ensemble-averaged energy as a function of sampled frequency number is shown. As highlighted in the figure, only Nω = 5   ×   102 sampled modes need to be used for the simulation to agree with the analytical result. The fact that Nω is low indicates that our method of vacuum mode selection is efficient.

Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
The inverse relation between the computation time and the number of processors. The data (black open square, blue, and red dot) follow an inverse relation y = C/x (black, blue, and red dashed lines). The parameter C is determined by the product of Np (number of particles) and Nω (number of sampled frequencies).
Details are in the caption following the image
Figure 11
Open in figure viewerPowerPoint
The ensemble-averaged energy of the SED harmonic oscillator and its convergence as a function of sampled frequency number Nω. The number of particles used in the simulation is Np = 2   ×   105, and the sampled frequency range is . The energy converges as the number of sampled frequencies Nω increases. At Nω = 5   ×   102 (blue cross), the deviation between the energy of the SED harmonic oscillator and the ground state energy of the quantum oscillator is 1%.

5. Conclusions

The analytical probability distribution of an SED harmonic oscillator is obtained in Section 2. The details of our numerical methods including vacuum mode selection are documented in Section 3. Agreement is found between the simulation and the analytical results, as both sequential sampling and ensemble sampling give the same probability distribution as the analytical result (see Figures 4 and 8). Numerical convergence is reached with a low number of sampled vacuum field mode (Nω = 5   ×   102), which is an indication that our method of vacuum mode selection ((32), (33), (34), and (37)) is effective in achieving a representative sampling.

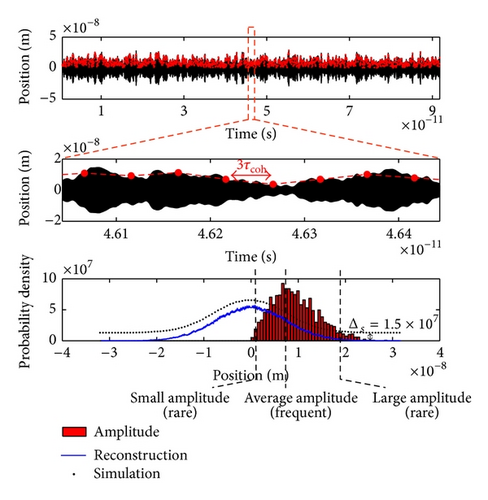
As the probability distribution constructed from a single trajectory is a Gaussian and satisfies the Heisenberg minimum uncertainty relation, we investigate the relation between the Gaussian probability distribution and the particle’s dynamical properties. As a result, the amplitude modulation of the SED harmonic oscillator at the time scale of τcoh is found to be the cause for the transitioning from the double-peak probability distribution to the Gaussian probability distribution (see Figures 5, 7, and 12).

Details are in the caption following the image
Figure 12
Open in figure viewerPowerPoint
A comparison between the harmonic oscillators with and without the vacuum field. Top: compared to Figure 1, it is clear from this figure that the SED harmonic oscillator undergoes an oscillatory motion with modulating oscillation amplitude. The oscillation amplitude modulates at the time scale of coherence time τcoh and is responsible for the resulting Gaussian probability distribution. Bottom: in the absence of the vacuum field or any external drive, a harmonic oscillator that is initially displaced from equilibrium performs a simple harmonic oscillation with constant oscillation amplitude. The resulting probability distribution has peaks at the two turning points.

6. Discussions: Application of Simulation to Other Physical Systems

In quantum mechanics, the harmonic oscillator has excited, coherent, and squeezed states. A natural extension of our current work is to search for the SED correspondence of such states. Currently, we are investigating how a Gaussian pulse with different harmonics of ω0 will affect the SED harmonic oscillator. Can the SED harmonic oscillator support a discrete excitation spectrum, and if so, how does it compare with the prediction from quantum mechanics? Such a study is interesting in the broader view of Milonni’s comment that SED is unable to account for the discrete energy levels of interacting atoms [1] and also Boyer’s comment that at present the line spectra of atoms are still unexplained in SED [36].

The methods of our numerical simulation may be applicable to study other quantum systems that are related to the harmonic oscillator, such as a charged particle in a uniform magnetic field and the anharmonic oscillator [5, 34]. For the first example, classically, a particle in a uniform magnetic field performs cyclotron motion. Such a system can be viewed as a two-dimensional oscillator, having the natural frequency set by the Larmor frequency. On the other hand, a quantum mechanical calculation for the same system reveals Landau quantization. The quantum orbitals of cyclotron motion are discrete and degenerate. Such a system presents a challenge to SED. For the second example, a harmonic potential can be modified to include anharmonic terms of various strengths. Heisenberg considered such a system a critical test in the early development of quantum mechanics [37, 38]. We think that a study of the anharmonic oscillator is thus a natural extension of our current study and may serve as a test for SED.

Lastly, over the last decades there has been a sustained interest to explain the origin of electron spin and the mechanism behind the electron double-slit diffraction with SED [15, 39–41]. Several attempts were made to construct a dynamical model that accounts for electron spin. In 1982, de la Peña calculated the phase averaged mechanical angular momentum of a three-dimensional harmonic oscillator. The result deviates from the electron spin magnitude by a factor of 2 [39]. One year later, Sachidanandam derived the intrinsic spin one-half of a free electron in a uniform magnetic field [40]. Whereas Sachidanandam’s calculation is based on the phase averaged canonical angular momentum, his result is consistent with Boyer’s earlier work where Landau diamagnetism is derived via the phase averaged mechanical angular momentum of an electron in a uniform magnetic field [5]. Although these results are intriguing, the most important aspect of spin, the spin quantization, has not been shown. If passed through a Stern-Gerlach magnet, will the electrons in the SED description split into two groups of trajectories (electron Stern-Gerlach effect is an interesting but controversial topic in its own right. Whereas Bohr and Pauli asserted that an electron beam cannot be separated by spin based on the concept of classical trajectories [42], Batelaan et al. [43, 44] and Dehmelt argue that one can do so with certain Stern-Gerlach-like devices [45, 46])? At this point, the dynamics become delicate and rather complex. To further investigate such a model of spin, a numerical simulation may be helpful.

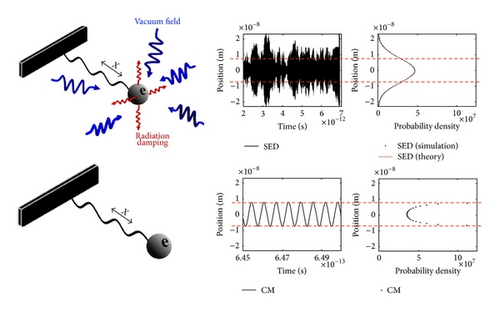
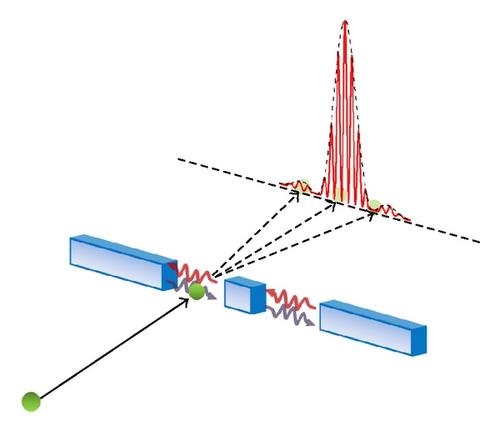
On the other hand, over the years claims have been made that SED can predict double-slit electron diffraction [4, 15, 41]. In order to explain the experimentally observed electron double-slit diffraction (see [47, 48] for a movie of the single electron buildup of a double-slit diffraction pattern) [49–51], different mechanisms motivated by SED were proposed [15, 41], but no concrete calculation has been given except for a detailed account of the slit-diffracted vacuum field [52]. In 1999, Kracklauer suggested that particles steered by the modulating waves of the SED vacuum field should display a diffraction pattern when passing through a slit, since the vacuum field itself is diffracted [41]. In recent years, another diffraction mechanism is proposed by Cavalleri et al. in relation to a postulated electron spin motion [15]. Despite these efforts, Boyer points out in a recent review article that at present there is still no concrete SED calculation on the double-slit diffraction [36]. Boyer suggests that as the correlation function of the vacuum field near the slits is modified by the slit boundary, the motion of the electron near the slits should be influenced as well. Can the scattering of the vacuum field be the physical mechanism behind the electron double-slit diffraction (see Figure 13)? As Heisenberg’s uncertainty relation is a central feature in all matter diffraction phenomena, any proposed mechanism for electron double-slit diffraction must be able to account for Heisenberg’s uncertainty relation. In the physical system of the harmonic oscillator, SED demonstrates a mechanism that gives rise to the Heisenberg minimum uncertainty. We hope that the current simulation method may help in providing a detailed investigation on the proposed SED mechanisms for the electron slit-diffraction.

Details are in the caption following the image
Figure 13
Open in figure viewerPowerPoint
Schematic illustration of a vacuum field based mechanism for electron double-slit diffraction. Several authors have proposed different SED mechanisms that explain the electron double-slit diffraction. The central idea is that the vacuum field in one slit is affected by the presence of the other slit. As the vacuum field perturbs the electron’s motion, an electron passing through only one slit can demonstrate a dynamical behavior that reflects the presence of both slits. Such a mechanism may reconcile the superposition principle with the concept of particle trajectory.

Acknowledgments

This work was completed utilizing the Holland Computing Center of the University of Nebraska. In particular, the authors thank Dr. Adam Caprez, Charles Nugent, Praga Angu, and Stephen Mkandawire for their work on parallelizing the SED simulation code. Huang thanks Dr. Bradley A. Shadwick, Roger Bach, and Dr. Steven R. Dunbar for stimulating discussions. This work is supported by NSF Grant no. 0969506.

    Appendices

    A. The Vacuum Field in Unbounded and Bounded Space

    In “unbounded” space, the modes are continuous and the field is expressed in terms of an integral. In “bounded” space, the modes are discrete and the field is expressed in terms of a summation. In both cases, the expression for the field amplitude needs to be obtained (see Appendices A.1 and A.2). The integral expression helps comparison with analytical calculations in previous papers [4–7, 9], while the summation expression is what we use in our numerical work.

    A.1. Unbounded Space

    The homogeneous solution of Maxwell’s equations in unbounded space is equivalent to the solution for a wave equation:
    ()
    where is the undetermined field amplitude for the mode (k, λ) and has the unit of electric field (V/m), is defined as the unit vector of k, and the two vectors, ε(k, 1) and ε(k, 2), describe an orthonormal polarization basis in a plane that is perpendicular to the wave vector k.
    Without loss of generality, a random phase can be factored out from the field amplitude :
    ()
    where . The field amplitude A(k, λ) can be determined through the phase averaged energy density:
    ()
    where ϵ0 is the vacuum permittivity, μ0 is the vacuum permeability, and is the random phase in (A.2). To evaluate the phase averaged energy density , we first calculate |E|2 and |B|2 using (A.2):
    ()
    where f ≡ f(k, λ; k′, λ′; r, t),
    ()
    The random phase average can be calculated with the following relation [9]:
    ()
    Applying (A.6) to (A.5), we obtain
    ()
    Consequently, and   can be evaluated using (A.4) and (A.7):
    ()
    The above calculation leads to a relation between the field amplitude A(k, λ) and the phase averaged energy density in unbounded space:
    ()
    Now, if we postulate that the vacuum energy is ℏω/2 for each mode (k, λ), then in a bounded cubic space of volume V the vacuum energy density is
    ()
    In the limit of unbounded space (i.e., V → ∞), the volume element Δ3k becomes differential (i.e., Δ3k → d3k) and the vacuum energy density becomes
    ()
    Comparing this result with (A.9), we find
    ()
    Assuming Avac(k, λ) is a positive real number, the vacuum field amplitude in unbounded space is determined:
    ()
    Therefore, the vacuum field in unbounded space is found to be
    ()
    which is (1).

    A.2. Bounded Space

    The solution of homogeneous Maxwell’s equations in bounded space has the summation form:
    ()
    where , is the undetermined field amplitude for the mode (k, λ) and has the unit of electric field (V/m), is defined as the unit vector of k, and the two vectors, εk,1 and εk,2, describe an orthonormal polarization basis in a plane that is perpendicular to the wave vector k.
    Using the relation (if the two modes are not identical (i.e., k′ ≠ k or λ′ ≠ λ), then and are independent, which leads to the factorization )
    ()
    we can follow the same argument in Appendix A.1 and obtain the phase averaged energy density in bounded space:
    ()
    where . Again, if we postulate that the vacuum energy is ℏω/2 for each mode (k, λ), then in a bounded space of volume V the vacuum energy density is
    ()
    Comparing (A.17) and (A.18), the vacuum field amplitude in bounded space is determined:
    ()
    Therefore, the RED vacuum field in bounded space is
    ()

    B. Isotropic Polarization Vectors

    A wave vector chosen along the z-axis,
    ()
    has an orthonormal polarization basis in the xy-plane:
    ()
    where the random angle χ is uniformly distributed in [0,2π]. To obtain the wave vector k in (32), can be first rotated counterclockwise about the y-axis by an angle θ and then counterclockwise about the z-axis by an angle ϕ. The corresponding rotation matrix is described by
    ()
    and k is obtained accordingly:
    ()
    In the same manner, we can rotate and with the rotation matrix and obtain an isotropically distributed (after the rotation, the uniformly distributed circle will span into a uniformly distributed spherical surface) polarization basis as described in (37):
    ()

    C. Repetitive Time

    A field composed of finite discrete frequencies,
    ()
    repeats itself at the least common multiple (LCM) of all the periods of its frequency components:
    ()
    ()
    where Tk = 2π/ωk. An example of a two-frequency beat wave is given in Figure 14. Given the frequency spectrum of E(t), one can draw a relation between the repetition time τrep and the greatest common divider (GCD) of the frequencies:
    ()
    The derivation of the relation in (C.4) is the following. First, we factorize the sum of all the frequencies into two terms:
    ()
    where nk are positive integers,
    ()
    Now, it is true that ; otherwise it would lead to a contradiction to (C.6). Therefore, one can conclude that
    ()
    From (C.3) and (C.7), the relation in (C.4)
    ()
    is drawn. Since the simulation should only be carried out through an integration time τint  ≤ τrep to avoid repetitive solutions, in our case the choice of the integration time (58)
    ()
    where Δω is the smallest frequency gap (Δω ≤ Δωgcd), suffices our purpose. The frequency gap as a function of κ can be estimated using (33):
    ()
    Applying the sharp resonance condition (9) to (23) and (34), it can be further shown that Δκ is much smaller than κ0 and κ≃κ0:
    ()
    where . Therefore, the size of Δω(κ) is approximately fixed within the sampled frequency range Δ, and the smallest frequency gap Δω can be approximated as
    ()
    Details are in the caption following the image
    Figure 14
    Open in figure viewerPowerPoint
    Repetition time of a beat wave. A beat wave (black solid line) is made of two frequency components (red and blue solid lines). The oscillation periods of the two frequency components are T1 = 1.5 and T2 = 2; thus the repetition time is τrep = [T1, T2] LCM = 6. Note that the periodicity of the envelope (black dashed line) is τenv = 12, which is different from the repetition time τrep = 6.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.