The time fractional Schrodinger equation (TFSE) for a nonrelativistic particle is derived on the basis of the Feynman path integral method by extending it initially to the case of a “free particle” obeying fractional dynamics, obtained by replacing the integer order derivatives with respect to time by those of fractional order. The equations of motion contain quantities which have “fractional” dimensions, chosen such that the “energy” has the correct dimension [ML²/T²]. The action S is defined as a fractional time integral of the Lagrangian, and a “fractional Planck constant” is introduced. The TFSE corresponds to a “subdiffusion” equation with an imaginary fractional diffusion constant and reproduces the regular Schrodinger equation in the limit of integer order. The present work corrects a number of errors in Naber’s work. The correct continuity equation for the probability density is derived and a Green function solution for the case of a “free particle” is obtained. The total probability for a “free” particle is shown to go to zero in the limit of infinite time, in contrast with Naber’s result of a total probability greater than unity. A generalization to the case of a particle moving in a potential is also given.

1. Introduction

There has been an explosive research output in recent years in the application of methods of fractional calculus [1–13] to the study of quantum phenomena [14–42]. The well-known Schrodinger equation with a first-order derivative in time and second-order derivatives in space coordinates was given by Schrodinger as an Ansatz. The Schrodinger equation has been generalized to (i) a space fractional Schrodinger equation involving noninteger order space derivatives but retaining first-order time derivative [14–18], (ii) a time fractional Schrodinger equation involving non-integer order time derivative but retaining the second-order space derivatives [19], or (iii) more general fractional Schrodinger equation where both time and space derivatives are of non-integer order [20–26]. The fractional Schrodinger equation has also been obtained by using a fractional generalization of the Laplacian operator [20] and by using a fractional variation principle and a fractional Klein-Gordon equation [36]. In all these cases the fractional derivatives employed have been the regular fractional derivatives of the Riemann-Liouville type or the Caputo type (generally used in physical applications with initial conditions) which are both nonlocal in nature. The fractional derivative which is nonlocal by definition can be made “local” by a limiting process as shown by Kolwankar and Gangal [41]. Highly irregular and nowhere differentiable functions can be analyzed locally using these local fractional derivatives. The Heisenberg principle in the fractional context has been investigated using local fractional Fourier analysis [42].

The Schrodinger equation for a free particle has the appearance of a diffusion equation with an imaginary diffusion coefficient. This suggests a method of deriving the Schrodinger equation as has been done using the Feynman path integral technique [43–45] based on the Gaussian probability distribution in the space of all possible paths. In other words, the classical Brownian motion leads to the Schrodinger equation in quantum mechanics. As far as deriving the fractional Schrodinger equation is concerned, the path integral approach for the Brownian-like paths for the Levy stable processes which leads to the classical space fractional diffusion equation has been extended to the Levy-like quantum paths leading to the space fractional Schrodinger equation (SFSE) in the seminal papers of Laskin [14–18]. It may be noted that in this case, the time derivative is still the integer first-order derivative; only the space part is of fractional order. The SFSE still retains the Markovian character and other fundamental aspects such as the Hermiticity of the Hamilton operator. Parity conservation and the current density have been explored in the space fractional quantum mechanics in terms of the Riesz fractional derivative. Applications of SFSE cover the dynamics of a free particle, particle in an infinite potential well, fractional Bohr atom, and the quantum fractional oscillator. Thus the space fractional Schrodinger equation appears to have been well established [18]. This theory has been further generalized recently within the frame work of tempered ultradistributions [39]. Thus the theory of SFSE can be considered fully established from the point of view of the Feynman path integral technique.

The fractional time derivative was introduced into the Schrodinger equation by Naber [19] by simply replacing the first-order time derivative by a derivative of non-integer order and retaining the second-order space derivatives intact. The resulting equation is referred to as the time fractional Schrodinger equation (TFSE). He did not derive the TFSE using the path integral or any other method. Naber carried out the time fractional modification to the Schrodinger equation in analogy with time fractional diffusion equation [19] but included the imaginary number i raised to a fractional power (the fractional degree being the same as the fractional order of the time derivative), implying a sort of the Wick rotation. In Naber’s opinion [19], the TFSE is equivalent to the usual Schrodinger equation, but with a time-dependent Hamiltonian. He obtained the solutions for a free particle and a particle in a potential well. A lot of subsequent work has been done on the TFSE, mostly based on Naber’s work [21–23, 28], including its generalization into space-time fractional quantum dynamics by including non-integer order derivatives in both time and space. Yet some basic questions have not been addressed. It has been observed that TFSE describes non-Markovian evolution and that the Green function in the form of the Mittag-Leffler function does not satisfy Stone’s theorem on one-parameter unitary groups and the semiclassical approximation in terms of the classical action is not defined [31]. There has been no derivation of TFSE on a basis similar to that of SFSE and it is the purpose of the present paper to rectify this lacuna. Since the path integral method of deriving the space fractional part of the Schrodinger equation is well established, the present paper concentrates only on deriving the time fractional Schrodinger equation from the Feynman path integral approach, leading to the time fractional Schrodinger equation as given by Naber. It may be pointed out that some results of Naber, such as the total probability being greater than unity, are difficult to understand physically. Moreover, several major errors in Naber’s paper have gone unnoticed and in fact have been repeated by workers who have followed his work. Furthermore, some of these authors have introduced errors of their own. Since many of the conclusions in Naber’s paper are based on derivations which include these errors, it calls for a reexamination of Naber’s generalization to the time fractional Schrodinger equation.

The present paper derives the time fractional Schrodinger equation using the Feynman path integral technique. It concentrates on the time fractional part only and not on the space fractional part as the theory of the latter has been well established in the works of Laskin [14–18]. Furthermore, the paper considers only the Caputo-type nonlocal fractional derivatives and not the local fractional derivatives discussed earlier. The paper starts from a generalization of the classical dynamics into fractional dynamics of a free particle and then adapting the Feynman technique derives the correct equations for TFSE. It is demonstrated that Naber’s result of probability being greater than unity is spurious and is a result of the ad hoc raising of the imaginary number i to a fractional power. The correct continuity equation for the probability density is also derived. The paper concludes with some new results.

2. Feynman Path Integral Method

The starting point for the Feynman method [43–46] is the classical Lagrangian

and the action

constructed from it. However, in view of the generalization to fractional calculus methods to be carried out later, the equations of motion of a classical particle in one dimension in the usual notation are considered first:

()

Integrating with respect to time yields

()

In the usual notation the Lagrangian is given by

()

and the action is given by

()

An outline of the Feynman path integral method is presented following very closely the account given by Feynman and Hibbs [43]. The essence of the Feynman path integral approach to quantum mechanics is in the probability amplitude (also known as the propagator or the Green function) K(x_b, t_b; x_a, t_a) for a particle starting from a position x_a at time t_a to reach a position x_b at a later time t_b, which arises from the contributions from all trajectories from x_a to x_b:

()

where the contribution from each of the paths has the form

()

Here S is the action defined in (5) and ℏ is Planck’s constant, the quantum of action. The time integral of the Lagrangian is to be taken along the path in question. Restricting to one dimension, the probability amplitude can be written as

()

The symbol 𝔇 indicates the fact that the operation of integration is carried over all paths from a to b.

The wave function ψ(x_b, t_b) gives the total probability amplitude to arrive at x_b at t_b satisfying (9), where the integral is taken over all possible values of x_a

()

The kernel K can be computed by first carrying out a “time slicing” operation by dividing the time interval from t_a to t_b into N segments of duration

()

where

()

where

()

is a line integral taken over the trajectory passing through the point x(t). The constant A is a normalizing factor.

The Schrodinger equation for a free particle in one dimension is derived by considering a special case of (9), which describes the evolution of the wave function from a time t_a to a time t_b, when t_b differs from t_a by an infinitesimal amount ε and applied to the case of a free particle. This step is based on the fact that the semiclassical approximation is valid not only in the limit of ℏ → 0 but also in the limit of small time interval [45]. The Kernel is proportional to the exponential of (i/ℏ) times the classical action for the infinitesimal time interval ε = t_b − t_a. With an obvious change of notation x_b = x, x_a = x₀, t_a = t, t_b = t + ε and using the fact that the particle is free, (2) yields

()

and (4) yields

()

and (5) yields for the action

()

As a consequence, (9) becomes

()

If x differs appreciably from x₀, the exponential in (17) oscillates very rapidly and the integral over x₀ contributes a very small value and only those paths which are very close to x give significant contributions. Changing the variable in the integral from x₀ to η = x − x₀ makes it ψ(x₀, t) = ψ(x + η, t). Since both ε and η are small quantities, ψ(x, t + ε) may be expanded in Taylor’s series and only up to terms of order ε are retained. On the right-hand side, ψ(x + η, t) may be expanded in Taylor’s series in powers of η, retaining terms up to second order in η (the integral involving the first-order term vanishes). Then (17) becomes

()

On the right-hand side the middle term vanishes on integration. It follows by equating the leading terms on both sides

()

Hence

()

Equating the remaining terms results in

()

This can be recognized as the diffusion equation with an imaginary diffusion coefficient or the Schrodinger equation for a free particle in quantum mechanics.

These considerations can be easily extended to the case of a particle moving in a potential field by incorporating a potential term V(x, t) in the Lagrangian L = T − V in (15). This will necessitate [43] incorporating an additional factor {1 − (iε/ℏ)V(x, t)} in (18), which becomes

()

Then (21) becomes

()

Multiplying both sides by −ℏ/i results in the standard Schrodinger equation of quantum mechanics:

()

It is to be noted that the imaginary number i on the left-hand side is not arbitrary; it arises from the coefficient of the potential term V in (23) but ultimately from the coefficient of S/ℏ in (7). This minor detail becomes important as will be discussed later in Section 8.

These considerations will be generalized for a particle obeying fractional dynamics. It can then be extended to the case of a particle in a potential field by including the potential term and making appropriate changes as will be described later.

3. Fractional Dynamics of a Free Particle

The first step is to generalize the equations of motion, (1)–(3), by replacing the integrals and derivatives by appropriate fractional integrals and derivatives. For physical problems with well-definable initial conditions the accepted practice is to employ the Caputo fractional derivatives [5]. The Caputo derivative of order β is defined by [3]:

()

In the limit β → n, the Caputo derivative becomes the ordinary nth derivative of the function.

The fractional integral of order β is defined by

()

In generalizing the equations of motion, the second-order time derivative in Newton’s law is replaced by a Caputo derivative of order α, and the first-order derivative is replaced by a Caputo derivative of order (α/2) [47]. Then (2) and (3) become

()

where as usual x₀,

refer to the initial position and initial value of the “fractional momentum” p_f, respectively. It is to be noted that the variables x, t are still the space and time variables and have the dimensions of length and time [L] and [T], respectively. However, the dynamical quantities obtained by the operation of fractional derivation have different dimensions; for example, “fractional velocity” with the notation

would have the units [L/T^α/2]. The dimension for the parameter “m_f” in the fractional momentum,

, is no longer just [M] but has to be chosen [47] so that the fractional quantity

has the dimensions of energy [ML²/T²]. Thus the dimension of the parameter “m_f” is [MT^2−α] and the fractional momentum has the dimensions [ML/T^2−α/2]. The Lagrangian in (4) when generalized has the dimensions of energy. Of course, all quantities regain the standard dimensions in the limit α → 2.

4. Time Fractional Schrodinger Equation for a Free Particle

There are two possible generalizations of the action integral in (5) used in fractional dynamics [11]:

()

Since the Lagrangian has the dimensions of energy, the dimensions of action defined in (28) and (29), S_I and S_II, are different.

The dimensions of S_I are the same as that of the regular action, namely, [ML²/T], but that of S_II is [ML²/T^2−α/2]. In the Newtonian limit α → 2, S_II→ regular action. These dimensional considerations have to be kept in mind in generalizing the Feynman method. In particular, if the choice from (29) is made, then a “fractional Planck constant” ℏ_f with appropriate dimensions must be introduced in order to render the argument of the exponential in (7) dimensionless.

For a “free particle” (27) yields

()

After carrying out the time slicing operation as in (11) and making the same approximation the evolution of the wave function in an infinitesimal interval of time ε can now be obtained. Equation (30) yields

()

and hence

()

But for action, there are two choices:

()

Making the appropriate changes, the equations for the evolution of the wave function in the two cases are

()

Changing the variable in the integrals from x₀ to η = x − x₀ as before and introducing two constants

()

Equations (36) and (37) can be written as

()

The left-hand sides of (39) and (40) can be expanded in fractional Taylor’s series [48] in time, with fractional derivative of order γ, and keeping only the lowest-order term in γ yields

()

In the right-hand side a Taylor expansion with terms up to second order in η with respect to space can be carried out and the two cases will be considered separately. Thus, the equation for ψ_I(x, t) becomes

()

On evaluating the integrals on the right-hand side of (42), the middle term with the first power of η vanishes. Equating the leading terms on both sides of (42) yields

, requiring that

. Equation (42) reduces to

()

Equating the remaining terms requires that the powers of ε must be the same on both sides; that is, γ = α − 1. Inserting the value of a_I and simplifying (43) yield

()

Similarly, by expanding (40) the equation for ψ_II(x, t) becomes

()

On evaluating the integrals on the right-hand side of (45) the middle term vanishes. Equating the leading terms on both sides of (45) as before yields for the normalizing factor

. Equation (45) reduces to

()

In the remaining terms, the powers of ε must be the same. This requires γ = α/2. Inserting the value of a_II and simplifying (46) yield the equation for the wave function ψ_II(x, t):

()

This completes the derivation based on the Feynman path integral method and (44) and (47) constitute the time fractional Schrodinger equations for a free particle corresponding to two ways of defining the action integral for a fractional dynamical system. In the limit α → 2, the fractional dynamical system goes over to the regular Newtonian system and in this case both (44) and (47) reduce to

()

given earlier, thus recovering the standard Schrodinger equation for a free quantum particle [49].

It should be noted that since α ≤ 2, with α = 2 being the limiting case, the order of the time fractional derivative is ≤1 in both (44) and (47) and cannot exceed 1. This means the time fractional Schrodinger equation as derived from the path integral method always corresponds to the “subdiffusion” case in contrast to the case where the TFSE is obtained by a simple replacement of the first-order time derivative by a fractional order derivative [19]. Furthermore, the order α/2 of the fractional derivative corresponds to the first-order regular derivative as has been used above in Section 3. Thus it appears that the second method of defining the action leading to (47) is the natural way to generalize to TFSE. In appearance also it is as if the equation has been obtained by replacing all quantities in the Schrodinger equation by an equivalent fractional quantity, except the space derivative. Furthermore, (44) becomes a fractional order integro-differential equation when α < 1 and no longer just a fractional order differential equation. Because of these reasons, it is considered the method of choice to use (47) as the TFSE derived from the path integral method and no further reference will be made to (44).

The coefficient of the space derivative term in (47) has the dimension [L²/T^α/2], corresponding to the fractional diffusion coefficient. Thus (47) can be considered a time fractional diffusion equation with an imaginary fractional diffusion coefficient, just as (48), the regular Schrodinger equation, can be considered to be a diffusion equation with an imaginary diffusion coefficient. Thus all the mathematical machinery of time fractional diffusion theory [5, 50–59] can be imported advantageously.

Although it is possible to introduce additional parameters and cast (47) in a dimensionless form, it has not been done here. However, for convenience, the subscript II is dropped from the wave function; a simplified notation for the Caputo derivative,

, with β = α/2 will be used. Naturally, 0 < β ≤ 1, and β → 1 yields the regular first-order time derivative, denoted by

. After incorporating these changes and defining a new constant D_f = ℏ_f/2m_f, (47) becomes

()

Equation (49) can be solved by a combination of the Fourier and Laplace transform methods [52–54].

5. Probability Current and the Continuity Equation

The probability density ρ is defined by ρ = ψ^*ψ = ψψ^*. The complex conjugate wave function satisfies

()

There is an identity satisfied by the Caputo derivative [5]

()

where the right-hand side represents the regular first-order derivative. This identity can be used in studying the time derivative of the probability density, given by

()

Inserting from (51) gives

()

Substituting from (49) and (50), (53) yields

()

Equation (54) can be rewritten after factoring out the constant and interchanging the order of space and time derivatives as

()

Introducing a new function

, (55) can be written as

()

Defining a probability current density given by

()

equation (56) can be written as

()

This is the time fractional version of the continuity equation. In the limit β → 1,

and (58) reproduce the continuity equation of standard quantum mechanics [49]. It may be noted that (58) differs from Naber’s result ((24) in [19]) and will be discussed later.

6. Solution for TFSE for a Free Particle

The solution for the TFSE for a free particle under the conditions

ψ(x, 0) = ψ₀(x); ψ(x, t) → 0, |x | → ∞, t > 0 is available in the literature but considered here for purposes of obtaining the Green function for the TFSE.

By applying the combined Fourier and Laplace transforms defined by

()

equation (49) reduces to

()

resulting in

()

Applying the inverse Laplace transform, (61) yields

()

in terms of the Mittag-Leffler function defined by a series or by the inverse Lapalce transform [3]:

()

The Green function solution can be written as

()

where the Green function is given by the inverse Fourier transform of the Mittag-Leffler function

()

where the Mittag-Leffler function has been defined [3] before in (63).

The Fourier inversion in (65) can be carried out [52–54] using the property that the Mittag-Leffler function is related through the Laplace integral to another special function of the Wright type denoted by

()

where the Wright function is defined by [54]

()

The Green function in (65) is then given by

()

In the context of fractional diffusion, the function M_β/2(z) belongs to the Wright type of probability densities characterized by the similarity variable

, where D_f is the fractional diffusion coefficient, with

. Furthermore, the probability densities are non-Markovian and exhibit a variance consistent with slow anomalous diffusion [49–51],

In the limit of β → 1, the probability density function goes over to the Gaussian

()

corresponding to regular diffusion. A plot of the reduced probability density function is given in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Reduced probability density function.

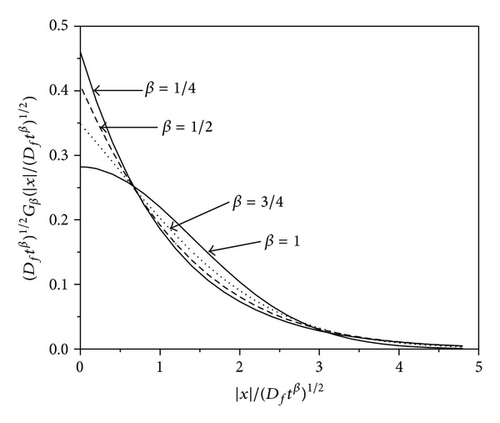
The Green function for regular diffusion describes a probability density, whereas the corresponding Green function for the Schrodinger equation is the propagator, which describes the probability amplitude for the particle to propagate from x_a at t_a to x_b at t_b. In exactly the same way, the Green function for time fractional diffusion describes a probability density, whereas the Green function in (68) is the fractional propagator and gives the probability amplitude. Of particular interest is the Fourier component of the wave function in (62) in connection with the total probability as t → ∞; the case discussed by Naber [19] and will be discussed in the next section.

7. Comments about Some Results in Naber’s Work [19]

This section draws attention to some errors in Naber’s paper which have gone unnoticed and have been reproduced repeatedly. Naber’s equations will be referred to by their number and a prefix N. Naber explicitly states that he uses the Caputo derivative, which has been defined earlier in (25) in this paper. Although Naber does not give the explicit definition of the Caputo fractional derivative in his paper [19], it can be inferred from (NA.3) given in the appendix to his paper.

(a) However, Naber writes in (N16) for a Caputo derivative of order (1 − ν), reproduced here for convenience in (70):

()

This is incorrect, as can be checked easily by taking the limit ν → 1. The left-hand side →ψ(t, x) as the derivative of zero order, but the right-hand side →0 because of the Γ function in the denominator. The correct form of equation is

()

As a consequence, the weight factor in (N18) should be (t − τ) ^1−ν and not (t − τ) ^−ν, which Naber uses to give a physical significance to the entity he has introduced. The correct weight factor in (N18) would →1 in the limit ν → 1.

(b) In (N11), Naber gives an identity satisfied supposedly by fractional Caputo derivatives of order less than 1, reproduced here for convenience in (72).

()

This identity is not correct and cannot be found anywhere. The identity satisfied by the Caputo derivatives is given in [5] and reproduced later in the current notation for ν < 1

()

This yields

and has been used earlier in (52) in this paper.

The incorrect identity has been used by Naber to derive an equation for the probability current, which is obviously incorrect. Unfortunately, the incorrect identity, as given by Naber, in (72) has been repeatedly used in the literature. The correct equation for the probability current has been given in this paper in (59), which reduces to the standard continuity equation for the probability current in regular quantum mechanics [49].

(c) This point concerns the separation of the Mittag-Leffler function with an imaginary argument into an oscillatory part and a part which decays exponentially with time. There is nothing wrong with the derivation itself as given by Naber, and the function under discussion is the Fourier component of the free particle wave function, in his notation

()

where E_ν(z) in Naber’s notation corresponds to the Mittag-Leffler function E_ν,1(z) defined in (63).

The Mittag-Leffler function with the complex argument has been separated into an oscillatory part and a part based on the evaluation of the inverse Laplace transform

()

along a Hankel contour and considering the contribution from the residue of the pole s₀ = σ^1/νi together with the contribution from the integral along the two strips on either side of the branch cut, which is a standard procedure. Naber finally gives the solution as

()

He argues that in the limit of t → ∞ the total probability arises basically from the first term and is equal to 1/ν², assuming that the wave function was initially normalized. Since ν < 1, the total probability is >1, a result difficult to understand physically. However, it is shown later that the solution derived in this paper yields a probability that →0 in the limit t → ∞.

The solution corresponding to (74) is given by (62) in this paper. The separation into two parts corresponding to (76) can be carried out by considering the inverse Laplace transform of (61):

()

As usual, the Bromwich contour is replaced by the Hankel contour. The two contributions arise from (i) the residue at the pole at s₀ = (D_fk²) ^1/β(−i) ^1/β and (ii) the integral along the two strips from 0 to −∞ introduced along the branch cut. The latter yields a contribution which decays in time just as the second term in Naber’s equation (76). The contribution from the residue is given by

()

and corresponds to the first term on the right-hand side in (76). However,

()

Therefore, (78) yields

()

The right-hand side of (80) has an amplitude term and an oscillatory factor. Because β < 1, cos (π/2β) is negative, the amplitude factor decays in time exponentially and →0 in the limit t → ∞. Thus the contribution from the residue due to the pole also →0. Thus the entire wave function →0 in the limit of t → ∞, so does the probability density. Hence the total probability also →0, in contrast to Naber’s result.

The question naturally arises why there is this difference in the two results, both of which are concerned with the Mittag-Leffler functions with complex arguments. The reason appears to be that in Naber’s case, the pole occurs at s₀ = σ^1/νi, whereas in the present paper, the pole occurs (using the same notation as Naber) at s₀ = σ^1/ν(−i) ^1/ν. The simple i in Naber’s case leads to the purely oscillatory solution and hence to the result of the probability being greater than unity. In our paper the imaginary number raised to the fractional power leads to the exponentially decaying solution and hence leads to the correct limit when t → ∞, namely, zero total probability. Naber’s result is a direct consequence of his choice to raise the power of the imaginary number i to the fractional power, so as to incorporate a Wick rotation. However, as had been indicated earlier, this imaginary number cannot be arbitrarily altered as it is connected with the phase factor iS/ℏ in the Feynman propagator. If it is necessary to include a Wick rotation, the power of i should be changed to ν + 1 in Naber’s equation (N9) instead of just ν. If this is done, the total probability would properly →0 in the limit t → ∞. If this is done, then the TFSE can be interpreted as the analytic continuation of the fractional diffusion equation, just as the regular Schrodinger equation can be considered as the analytic continuation of the regular diffusion equation.

8. TFSE for a Particle in a Potential Field

So far attention has been focused on a free particle. These considerations can be easily extended to the case of a particle moving in a potential field by incorporating a potential term V(x, t) in the Lagrangian L = T − V. This will necessitate incorporating an additional term −V(x, t)ε^α/2/Γ(1 + α/2) in the right-hand side of (35) and an additional factor −(i/h_f)(V(x, t)ε^α/2/Γ(1 + α/2)) in the exponential in (37). This results in changing (45) into

()

Equation (47) then becomes

()

Multiplying both sides by −ℏ_f/i results in the FTSE for a particle in a potential field as

()

which reduces to the standard Schrodinger equation of quantum mechanics:

()

One final remark needs to be made concerning the use of the Planck units for casting the TFSE in terms of dimensionless quantities. After the derivation, the FTSE in (83) can be cast in dimensionless quantities; however, the appropriate fractional Planck units must be defined to take care of the fractional quantities involved in (83).

9. Discussion and Conclusions

The TFSE has been derived using the Feynman path integral technique for a nonrelativistic particle. As expected the TFSE looks like a time fractional diffusion equation with an imaginary fractional diffusion constant but pertains to the realm of subdiffusion only, in contrast to Naber’s generalization which includes superdiffusion as well. This is understandable because the case considered in this paper pertains to the nonrelativistic case. Relativistic considerations would have to be included for the superdiffusion case, which would lead to the Klein-Gordon equation in the integer order limit. In adapting the Feynman method, it is shown that it is preferable to introduce the action S as a fractional time integral of the Lagrangian and that it is necessary to introduce a “fractional Planck constant.” In the limit of integer order, the regular action S, the regular Schrodinger equation, and the regular Planck constant are all recovered. It may be of interest to note that there is a fractional Planck constant implied in Naber’s work also, although it is not explicitly so stated. His equations are rendered nondimensional by using the Planck units of mass, length, and time and then generalized to fractional derivatives after including a Wick rotation. This implies a change of variable of time t → it so that the imaginary number is raised to the same power as the order of the fractional time derivative involved. However, the Planck units may not be the appropriate quantities as the equations involve quantities of fractional dimension and the equations must be made nondimensional after the generalization to fractional derivatives and not before. A fractional Planck constant does show up in Naber’s treatment as well, as the ratio of masses m/M_p [31, 32].

A number of errors in Naber’s work have been corrected. The correct continuity equation for the probability current is derived and the Green function solution for a free particle is given. The Green function is given in terms of a special type of function, the M-Wright function, which is used extensively in studies of time fractional subdiffusion studies. In the context of time fractional diffusion, the M-Wright function is a probability density function in time, which is non-Markovian and goes over to the Gaussian in the nonfractional limiting case. In the context of TFSE, the M-Wright function gives the propagator, which is a probability amplitude. Probability considerations are accounted for by the usual process of squaring of the amplitude. In particular, it is shown that Naber’s result that the total probability is greater than unity in the long-time limit is a spurious result arising out of the operation of arbitrarily raising of the imaginary number i to the power of the same degree as the fractional time derivative invoking a Wick rotation. It is shown that such arbitrary change of the imaginary number cannot be carried out as the imaginary number i is connected with the phase of the action S in the path integral contribution. However, if we desired to consider a Wick rotation, it should be included as an additional increase of the index of the power of the imaginary number. The TFSE for a particle moving in a potential field is also derived. Furthermore, it is suggested that even in studies of fractional classical mechanics, such as those using variational methods, the action integral be expressed as a time fractional integral of the Lagrangian. Further extensions including the solutions to particle subject to different potentials are underway.

References

1 Oldham K. B. and Spanier J., The Fractional Calculus, 1974, Academic Press, New York, NY, USA, MR0361633, ZBL0292.26011.
Google Scholar
2 Miller K. S. and Ross B., An Introduction to the Fractional Calculus and Fractional Differential Equations, 1993, John Wiley & Sons, New York, NY, USA, A Wiley-Interscience Publication, MR1219954, ZBL0943.82582.
Google Scholar
3 Podlubny I., Fractional Differential Equations, 1999, 198, Academic Press, San Diego, Calif, USA, Mathematics in Science and Engineering, MR1658022, ZBL1056.93542.
Google Scholar
4 Samko S. G., Kilbas A. A., and Marichev O. I., Fractional Integrals and Derivatives: Theory and Applications, 1993, Gordon and Breach Science Publishers, Yverdon, Switzerland, MR1347689, ZBL0924.44003.
Google Scholar
5 Carpinteri A. and Mainardi F., Fractals and Fractional Calculus in Continuum Mechanics, 1997, 378, Springer, Vienna, Austria, CISM Courses and Lectures, MR1611582, ZBL0964.33011.
Google Scholar
6 Hilfer R., Applications of Fractional Calculus in Physics, 2000, World Scientific Publishing, River Edge, NJ, USA, https://doi.org/10.1142/9789812817747, MR1890104, ZBL1059.47501.
Google Scholar
7 West B. J., Bologna M., and Grigolini P., Physics of Fractal Operators, 2003, Springer, New York, NY, USA, Institute for Nonlinear Science, https://doi.org/10.1007/978-0-387-21746-8, MR1988873, ZBL1256.37039.
10.1007/978-0-387-21746-8
Google Scholar
8 Magin R. L., Fractional Calculus in Bioengineering, 2006, Begell House, Redding, Conn, USA.
Google Scholar
9 Debnath L. and Bhatta D., Integral Transforms and Their Applications, 2007, 2nd edition, Chapman & Hall/CRC, Boca Raton, Fla, USA, MR2253985, ZBL1233.35165.
Google Scholar
10 Hermann R., Fractional Calculus, 2011, World Scientific, Singapore.
Google Scholar
11 Malinowska A. B. and Torres D. F. M., Introduction to the Fractional Calculus of Variations, 2012, Imperial College Press, London, UK, MR2984893, ZBL1259.49005.
Google Scholar
12 Baleanu D., Diethelm K., Scalas E., and Trujillo J. J., Fractional Calculus: Models and Numerical Methods, 2012, 3, World Scientific Publishing, Hackensack, NJ, USA, Series on Complexity, Nonlinearity and Chaos, https://doi.org/10.1142/9789814355216, MR2894576, ZBL1258.35201.
Google Scholar
13 GolmanKhaneh A. K., Investigations in Dynamics:With Focus on Fractal Dynamics, 2012, Lap Lambert Academic Publishing.
Google Scholar
14 Laskin N., Fractional quantum mechanics, Physical Review E. (2000) 62, no. 3, 3135–3145, 2-s2.0-0034271488, https://doi.org/10.1103/PhysRevE.62.3135.
Google Scholar
15 Laskin N., Fractional quantum mechanics and Lévy path integrals, Physics Letters A. (2000) 268, no. 4–6, 298–305, https://doi.org/10.1016/S0375-9601(00)00201-2, MR1755089, ZBL0948.81595.
10.1016/S0375-9601(00)00201-2
Google Scholar
16 Laskin N., Fractional Schrödinger equation, Physical Review E. (2002) 66, no. 5, 7, 056108, https://doi.org/10.1103/PhysRevE.66.056108, MR1948569.
Google Scholar
17 Laskin N., Fractals and quantum mechanics, Chaos. (2000) 10, no. 4, 780–790, https://doi.org/10.1063/1.1050284, MR1802665, ZBL1071.81513.
Google Scholar
18 Laskin N., Principles of fractional quantum mechanics, http://arxiv.org/abs/1009.5533.
Google Scholar
19 Naber M., Time fractional Schrödinger equation, Journal of Mathematical Physics. (2004) 45, no. 8, 3339–3352, https://doi.org/10.1063/1.1769611, MR2077514, ZBL1071.81035.
Google Scholar
20 Saxena R. K., Saxena R., and Kalla S. L., Solution of space-time fractional Schrödinger equation occurring in quantum mechanics, Fractional Calculus & Applied Analysis. (2010) 13, no. 2, 177–190, MR2723852, ZBL1211.26010.
Google Scholar
21 Wang S. and Xu M., Generalized fractional Schrödinger equation with space-time fractional derivatives, Journal of Mathematical Physics. (2007) 48, no. 4, 10, 043502, https://doi.org/10.1063/1.2716203, MR2319896, ZBL1137.81328.
Google Scholar
22 Dong J. and Xu M., Space-time fractional Schrödinger equation with time-independent potentials, Journal of Mathematical Analysis and Applications. (2008) 344, no. 2, 1005–1017, https://doi.org/10.1016/j.jmaa.2008.03.061, MR2426328, ZBL1140.81357.
Google Scholar
23 Guo X. and Xu M., Some physical applications of fractional Schrödinger equation, Journal of Mathematical Physics. (2006) 47, no. 8, 9, 082104, https://doi.org/10.1063/1.2235026, MR2258580, ZBL1112.81028.
Web of Science® Google Scholar
24 Jiang X. Y., Time-space fractional Schrödinger like equation with a nonlocal term, European Physical Journal: Special Topics. (2011) 193, no. 1, 61–70, 2-s2.0-79953709420, https://doi.org/10.1140/epjst/e2011-01381-7.
Google Scholar
25 Dong J., Fractional Green′s function for the time-dependent scattering problem in the space-time-fractional quantum mechanics, http://arxiv.org/abs/1301.3206.
Google Scholar
26 Dong J. and Xu M., Applications of continuity and discontinuity of a fractional derivative of the wave functions to fractional quantum mechanics, Journal of Mathematical Physics. (2008) 49, no. 5, 16, 052105, https://doi.org/10.1063/1.2917067, MR2421898, ZBL1152.81405.
Google Scholar
27 Scalas E., Baleanu D., Mainardi F., and Mura A., Fractional calculus and the Schrodinger equation, Proceedings of the 2nd IFAC Workshop on Fractional Differentiation and Its Applications, July 2006, Porto, Portugal.
Google Scholar
28 Bhatti M., Fractional Schrödinger wave equation and fractional uncertainty principle, International Journal of Contemporary Mathematical Sciences. (2007) 2, no. 17–20, 943–950, MR2371326, ZBL1146.35082.
10.12988/ijcms.2007.07096
Google Scholar
29 Wang S., Xu M., and Li X., Green′s function of time fractional diffusion equation and its applications in fractional quantum mechanics, Nonlinear Analysis: Real World Applications. (2009) 10, no. 2, 1081–1086, https://doi.org/10.1016/j.nonrwa.2007.11.024, MR2474283, ZBL1167.35441.
Google Scholar
30 Tofighi A., Probability structure of time fractional schrodinger equation, Acta Physica Polonica A. (2009) 116, no. 2, 114–118, 2-s2.0-69849090958.
Google Scholar
31 Iomin A., On fractional time quantum dynamics, Physical Review E. (2009) 80, no. 2, 4, 022103, https://doi.org/10.1103/PhysRevE.80.022103.
Google Scholar
32 Iomin A., Fractional-time Schrödinger equation: fractional dynamics on a comb, Chaos, Solitons & Fractals. (2011) 44, no. 4-5, 348–352, https://doi.org/10.1016/j.chaos.2011.03.005, MR2795940, ZBL1225.81053.
Google Scholar
33 Shahin A. M., Ahmed E., and Omar Y. A., On fractional order quantum mechanics, International Journal of Nonlinear Science. (2009) 8, no. 4, 469–472, MR2595466.
Google Scholar
34 Rozmej P. and Bandrowski B., On fractional Schrödinger equation, Computational Methods in Science and Technology. (2010) 16, 191–194.
Google Scholar
35 Ertik H., Demirhan D., Şirin H., and Büyükkılıç F., Time fractional development of quantum systems, Journal of Mathematical Physics. (2010) 51, no. 8, 15, 082102, https://doi.org/10.1063/1.3464492, MR2683515.
Google Scholar
36 Muslih S. I., Agrawal O. P., and Baleanu D., A fractional Schrödinger equation and its solution, International Journal of Theoretical Physics. (2010) 49, no. 8, 1746–1752, https://doi.org/10.1007/s10773-010-0354-x, MR2673198, ZBL1197.81126.
Google Scholar
37 Chaurasia V. B. L. and Kumar D., Solutions of Unified fractional Schrödinger equation, ISRN Mathematical Physics. (2012) 2012, 7, https://doi.org/10.5402/2012/935365, 935365.
10.5402/2012/935365
Google Scholar
38 Mahata A. K., On fractional Schrödinger equation and its application, International Journal of Scientific Engineering Research. (2013) 4, 1–5.
Google Scholar
39 de Paoli A. L. and Rocca M. C., The fractionary Schrödinger equation, Green functions and ultradistributions, Physica A. (2013) 392, no. 1, 111–122, https://doi.org/10.1016/j.physa.2012.08.017, MR2983968.
Google Scholar
40 Oliveira E. C., Costa F. S., and VazJ.Jr., The fractional Schrödinger equation for delta potentials, Journal of Mathematical Physics. (2010) 51, no. 12, 16, 123517, https://doi.org/10.1063/1.3525976, MR2779619.
Google Scholar
41 Kolwankar K. M. and Gangal A. D., Fractional differentiability of nowhere differentiable functions and dimensions, Chaos. (1996) 6, no. 4, 505–513, https://doi.org/10.1063/1.166197, MR1425755, ZBL1055.26504.
Google Scholar
42 Yang X. J., Baleanu D., and Machado J. A. T., Mathematical aspects of the Heisenberg uncertainty principle within local fractional Fourier analysis, Boundary Value Problems. (2013) 2013, no. article 131, https://doi.org/10.1186/1687-2770-2013-131.
Google Scholar
43 Feynman R. P. and Hibbs A. R., Quantum Mechanics and Path Integrals, 1965, McGraw-Hill, New York, NY, USA.
Google Scholar
44 Kleinert H., Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 2006, World Scientific Publishing, Singapore.
Google Scholar
45 Schulman L. S., Techniques and Applications of Path Integration, 1981, John Wiley & Sons, New York, NY, USA, MR601595.
Google Scholar
46 Kac M., Probability and Related Topics in Physical Sciences, 1957, Interscience, London, UK.
Google Scholar
47 Narahari Achar B. N., Hanneken J. W., Becker N., and Morgan M., Intrinsic dissipation in fractional order dynamics, Proceedings of the International Workshop on Fractional Differentiation and Its Applications (FDA ′10), October 2010, Badajoz, Spain.
Google Scholar
48 Narahari Achar B. N. and Hanneken J. W., Fractional order dynamics under gravity, Proceedings of the International Workshop on Fractional Differentiation and Its Applications (FDA ′10), October 2010, Badajoz, Spain.
Google Scholar
49 Schiff L. I., Quantum Mechanics, 1968, McGraw-Hill, New York, NY, USA.
Google Scholar
50 Mainardi F., Paradisi P., and Gorenflo R., J. Kertesz and I. Kondov, Probability distributions generated by fractional order diffusion equations, Econophysics: An Emerging Science, 1998, Kluwer Academic Publishers, Dordrecht, The Netherlands.
Google Scholar
51 Gorenflo R., Iskenderov A., and Luchko Y., Mapping between solutions of fractional diffusion-wave equations, Fractional Calculus & Applied Analysis. (2000) 3, no. 1, 75–86, MR1743407, ZBL1033.35161.
Google Scholar
52 Mainardi F., Luchko Y., and Pagnini G., The fundamental solution of the space-time fractional diffusion equation, Fractional Calculus & Applied Analysis. (2001) 4, no. 2, 153–192, MR1829592, ZBL1054.35156.
Google Scholar
53 Mainardi F., The time fractional diffusion-wave equation, Radiofisica. (1996) 38, no. 1-2, 20–36.
Google Scholar
54 Mainardi F., The fundamental solutions for the fractional diffusion-wave equation, Applied Mathematics Letters. (1996) 9, no. 6, 23–28, https://doi.org/10.1016/0893-9659(96)00089-4, MR1419811, ZBL0879.35036.
10.1016/0893-9659(96)00089-4
Web of Science® Google Scholar
55 Mainardi F. and Pagnini G., The role of the Fox-Wright functions in fractional sub-diffusion of distributed order, Journal of Computational and Applied Mathematics. (2007) 207, no. 2, 245–257, https://doi.org/10.1016/j.cam.2006.10.014, MR2345245, ZBL1120.35002.
Google Scholar
56 Mainardi F., Mura A., and Pagnini G., The M-Wright function in time-fractional diffusion processes: a tutorial survey, International Journal of Differential Equations. (2010) 2010, 29, 104505, https://doi.org/10.1155/2010/104505.
10.1155/2010/104505
Google Scholar
57 Gorenflo R., Luchko Y., and Mainardi F., Analytical properties and applications of the Wright function, Fractional Calculus & Applied Analysis. (1999) 2, no. 4, 383–414, MR1752379, ZBL1027.33006.
Google Scholar
58 Gorenflo R., Mainardi F., Moretti D., Pagnini G., and Paradisi P., Fractional diffusion: probability distributions and random walk models, Physica A. (2002) 305, no. 1-2, 106–112, https://doi.org/10.1016/S0378-4371(01)00647-1, MR1923936.
Google Scholar
59 Mainardi F., Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models, 2010, Imperial College Press, London, UK, https://doi.org/10.1142/9781848163300, MR2676137.
Google Scholar

Citing Literature

All articles

Time Fractional Schrodinger Equation Revisited

Abstract

1. Introduction

2. Feynman Path Integral Method

3. Fractional Dynamics of a Free Particle

4. Time Fractional Schrodinger Equation for a Free Particle

5. Probability Current and the Continuity Equation

6. Solution for TFSE for a Free Particle

7. Comments about Some Results in Naber’s Work [19]

8. TFSE for a Particle in a Potential Field

9. Discussion and Conclusions

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Time Fractional Schrodinger Equation Revisited

Abstract

1. Introduction

2. Feynman Path Integral Method

3. Fractional Dynamics of a Free Particle

4. Time Fractional Schrodinger Equation for a Free Particle

5. Probability Current and the Continuity Equation

6. Solution for TFSE for a Free Particle

7. Comments about Some Results in Naber’s Work [19]

8. TFSE for a Particle in a Potential Field

9. Discussion and Conclusions

References

Citing Literature

Figures

References

Related

Information