The state estimation problem is investigated for neural networks with leakage delay and time-varying delay as well as for general activation functions. By constructing appropriate Lyapunov-Krasovskii functionals and employing matrix inequality techniques, a delay-dependent linear matrix inequalities (LMIs) condition is developed to estimate the neuron state with some observed output measurements such that the error-state system is globally asymptotically stable. An example is given to show the effectiveness of the proposed criterion.

1. Introduction

In the past few years, neural networks have been extensively studied and successfully applied in many areas such as combinatorial optimization, signal processing, associative memory, affine invariant matching, and pattern recognition [1]. In such applications, the stability analysis is a necessary step for the practical design of neural networks [2]. In hardware implementation, time delays occur due to finite switching speed of the amplifiers and communication time. The existence of time delay may lead to some complex dynamic behaviors such as oscillation, divergence, chaos, instability, or other poor performance of the neural networks [3]. Therefore, the issue of stability analysis of neural networks with time delay attracts many researchers, and a number of remarkable results have been built up in the open literature; for example, see [2–5] and references therein.

When a neural network is designed to handle complex nonlinear problems, a great number of neurons with tremendous connections are often required. In such relatively large-scale neural networks, it may be very difficult and expensive (or even impossible) to obtain the complete information of the neuron states. On the other hand, in many practical applications, one needs to know the neuron states and then use them to achieve certain objectives. For instance, a recurrent neural network was presented in [6] to model an unknown nonlinear system, and the neuron states were utilized to implement a control law. Therefore, it is of great importance to study the state estimation problem of neural networks.

Recently, some results related to the state estimation problem for neural networks have been reported; for example, see [7–38] and references therein. In [7], authors initially studied the state estimation problem of delayed neural networks, where a delay-independent condition was obtained in terms of a linear matrix inequality (LMI). In [8], authors proposed a free-weighting matrix approach to discuss the state estimation problem for neural networks with time-varying delay. By using the Newton-Leibniz formula, some slack variables were introduced to derive a less conservative condition. In [11], attention was focused on the design of a state estimator to estimate the neuron states by using the delay-fractioning technique to reduce the possible conservatism. The authors in [13] first investigated the robust state estimator problem of delayed neural networks with parameter uncertainties. Delay-dependent conditions were presented to guarantee the global asymptotical stability of the error system. In [16], a further result on design problem of state estimator for a class of neural networks of neutral type was presented. A delay-dependent LMI criterion for existence of the estimator was derived. In [20], the state estimation problem for discrete neural networks with partially unknown transition probabilities and time-varying delays was discussed. By utilizing a novel Lyapunov functional integrating both lower and upper time-delay bounds and some new techniques, some delay-range-dependent sufficient conditions under which the estimation error dynamics were stochastically stable are established. In [22], authors investigated the state estimation problem for neural networks with discrete time-varying delay and distributed time-varying delay; a delay-interval-dependent condition is developed to estimate the neuron state with some observed output measurements such that the error-state system was globally asymptotically stable. In [25], leakage delay in the leakage term was used to destabilize the neuron states. By constructing the Lyapunov-Krasovskii functional which contains a triple-integral term, an improved delay-dependent stability criterion was derived in terms of LMIs. In [27], the state estimation problem for a class of discrete-time stochastic neural networks with random delays was considered. By employing a Lyapunov-Krasovskii functional, sufficient delay distribution- dependent conditions were established in terms of LMIs that guarantee the existence of the state estimator. In [33], authors discussed the state estimation problem for Takagi-Sugeno (T-S) fuzzy Hopfield neural networks via strict output passivation of the error system. In [36–38], authors investigated the distributed state estimation problem for sensor networks and presented several new sufficient conditions to guarantee the convergence of the estimation error systems. To the best of the author’s knowledge, there are no results on the problem of state estimation for neural networks with leakage delay and time-varying delays. As pointed out in [39], neural networks with leakage delay are a class of important neural networks; time delay in the leakage term also has great impact on the dynamics of neural networks since time delay in the stabilizing negative feedback term has a tendency to destabilize a system. Therefore, it is necessary to investigate the state estimation problem for neural networks with leakage delay [25].

Motivated by the previous discussions, the objective of this paper is to study the state estimation for neural networks with leakage delay and time-varying delays by employing new Lyapunov-Krasovskii functionals and using matrix inequality techniques. The obtained sufficient condition does not require the differentiability of time-varying delays and is expressed in terms of linear matrix inequalities, which can be checked numerically using the effective LMI toolbox in Matlab. An example is given to show the effectiveness of the proposed criterion.

Notations. The notations are quite standard. Throughout this paper, ℝⁿ and ℝ^n×m denote, respectively, the n-dimensional Euclidean space and the set of all n × m real matrices. ∥·∥ refers to the Euclidean vector norm. A^T represents the transpose of matrix A, and the asterisk “*” in a matrix is used to represent the term which is induced by symmetry. I is the identity matrix with compatible dimension. X > Y means that X and Y are symmetric matrices and that X − Y is positive definite. Matrices, if not explicitly specified, are assumed to have compatible dimensions.

2. Model Description and Preliminaries

Consider the following neural networks with leakage delay and time-varying delays:

()

for t ≥ 0, where x(t) = (x₁(t), x₂(t), …, x_n(t)) ^T ∈ ℝⁿ is the state vector of the network at time t, and n corresponds to the number of neurons; C ∈ ℝ^n×n is a positive diagonal matrix, and A ∈ ℝ^n×n and B ∈ ℝ^n×n are the connection weight matrix and the delayed connection weight matrix, respectively; f(x(t)) = (f₁(x₁(t)), f₂(x₂(t)), …, f_n(x_n(t))) ^T ∈ ℝⁿ denotes the neuron activation at time t; J(t) ∈ ℝⁿ is an external input vector; δ and τ(t) denote the leakage delay and time-varying delay, respectively.

Throughout this paper, we make the following assumptions.

(H1) (see [40]) For any j ∈ {1,2, …, n} there exist constants

and

such that

()

for all α₁ ≠ α₂.

(H2) (see [25]) The leakage delay δ and time-varying delays τ(t) satisfy the following conditions:

()

where δ and τ are constants.

As is well known, information about the neuron states is often incomplete from the network measurements (outputs) in applications, and the network measurements are subject to nonlinear disturbances. Similar to [7], we assume that the network measurements satisfy

()

where y(t) ∈ ℝ^m is the measurement output, and D ∈ ℝ^m×n is a known constant matrix with appropriate dimension. g : ℝ × ℝⁿ → ℝ^m is the neuron-dependent nonlinear disturbances on the network outputs and satisfies the following condition.

(H3) (see [22]) For any j ∈ {1,2, …, m} there exist constants

and

such that

()

for t ≥ 0 and all α₁(t) ≠ α₂(t).

Remark 1. As pointed out in [40], the constants and in assumption (H1) of this paper are allowed to be positive, negative, or zero. Hence, assumption (H1), first proposed by Liu et al. in [40], is weaker than the Lipschitz condition.

For the delay neural networks (1), we construct the full-order state estimation as follows:

()

where u(t) ∈ ℝⁿ is an estimation of the state x(t) of (1), and K ∈ ℝ^n×m, to be determined, is a gain matrix of the state estimator.

Let the error state be e(t) = x(t) − u(t) then it follows from (1), (4), (6), and (7) that

()

where h(e(t)) = f(x(t)) − f(u(t)), r(t, e(t)) = g(t, x(t)) − g(t, u(t)).

The problem to be addressed in this study is to find out the gain matrix K such that the system (8) is globally asymptotically stable.

To prove our results, the following lemmas that can be found in [22] are necessary.

Lemma 2 (see [22].)For any constant matrix W ∈ ℝ^m×m, W > 0, scalar 0 < h(t) < h, and vector function ω(·):[0, h] → ℝ^m such that the integrations concerned are well defined, then

()

Lemma 3 (see [22].)Given constant matrices P, Q, and R, where P^T = P, Q^T = Q, then

()

is equivalent to the following conditions:

()

3. Main Results

For presentation convenience, in the following, we denote

()

Theorem 4. Assume that the assumptions (H1)–(H3) hold. If there exist four symmetric positive definite matrices P_i (i = 1,2, 3,4), five positive diagonal matrices W₁, W₂, R₁, R₂, and R₃, and seven matrices Q₁, Q₂, Q₃, X₁₁, X₁₂, X₂₂, and Z, such that the following LMIs hold:

()

where

, = X₁₁ − F₁W₁ + F₂W₂ − Q₁ − D^TZ^T, Ω₁₅ = −X₁₂ − Q₁C, Ω₁₇ = Q₁A + F₄R₁, Ω₁₉ = −Z + G₂R₃,

, Ω₂₇ = W₁ − W₂ + Q₁A,

, then error-state system (8) of the delayed neural network described by (1) and (6) is globally asymptotically stable, and the estimator gain matrix K can be designed as

Proof. From assumption (H1), we know that

()

Let W₁ = diag (w₁₁, w₁₂, …, w_1n), W₂ = diag (w₂₁, w₂₂, …, w_2n), and consider the following Lyapunov-Krasovskii functional as

()

where

()

Calculating the time derivative of V_i(t) (i = 1,2, 3,4), we obtain

()

In deriving inequality (21), we have made use of Lemma 2. It follows from inequalities (19)–(22) that

()

From model (8), we have

()

By Newton-Leibniz formulation and assumption (H2), we have

()

In addition, for positive diagonal matrices R_i > 0 (i = 1,2, 3), we can get from assumption (H1) and assumption (H3) that [15]

()

It follows from (23)–(26) that

()

where ξ(t) = (e^T(t),

, e^T(t − τ(t)), e^T(t − τ), e^T(t − δ),

, h^T(e(t)), h^T(e(t − τ(t))), r^T(t, e(t))) ^T,

()

with

By using Lemma 3, and noting , it is easy to verify the equivalence of Π < 0 and Ω < 0. Thus, one can derive from (14) and (27) that

()

which implies that the error-state system (8) of the delayed neural networks described by (1) and (6) is globally asymptotically stable. The proof is completed.

4. Numerical Example

To verify the effectiveness of the theoretical result of this paper, consider the following example.

Example 1. Consider a two-neuron neural network (1), where

()

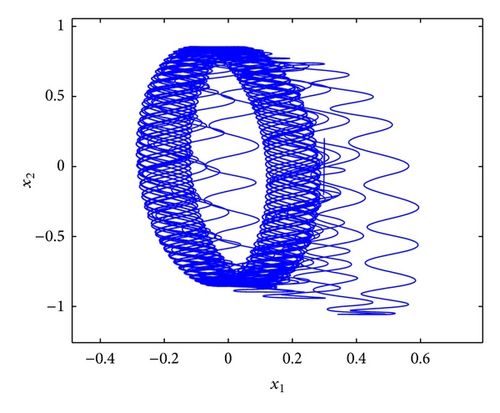
Figure 1 shows that the considered neural network has a chaotic attractor, where the initial condition is x₁(t) = 0.5cos (0.5t), x₂(t) = −0.2sin (18t), and t ∈ [−0.27,0].

It can be verified that assumptions (H1) and (H2) are satisfied, and F₁ = 0, F₂ = I, F₃ = 0, F₄ = diag {0.5,0.5}, τ = 0.27.

Choose network measurement (4), where

()

It is obvious that assumption (H3) is satisfied with G₁ = −0.01I and G₂ = 0. By the Matlab LMI Control Toolbox, we find a solution to the LMIs in (13) and (14) as follows:

()

Subsequently, we can obtain from that

()

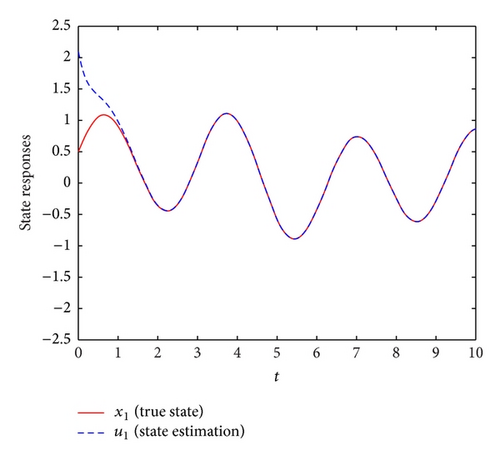
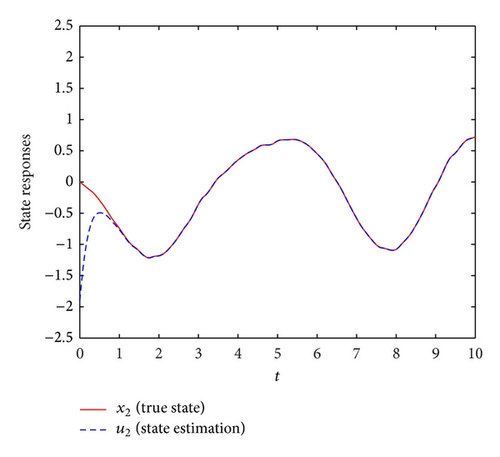
Therefore, we know from Theorem 4 that error-state system (8) of the delayed neural network described by (1) and (6) is globally asymptotically stable. The simulation results are shown in Figures 2 and 3, which demonstrate the effectiveness of the developed approach for the design of the state estimator for neural networks with leakage delay and time-varying delay.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Phase trajectory of model (1).

5. Conclusions

In this paper, the state estimation problem has been investigated for neural networks with leakage delay and time-varying delay as well as general activation functions. By employing Lyapunov functional method and the matrix inequality techniques, a delay-dependent LMIs condition has been established to estimate the neuron state with some observed output measurements such that the error-state system is globally asymptotically stable. An example has been provided to show the effectiveness of the proposed criterion.

Acknowledgments

The authors would like to thank the reviewers and the editor for their valuable suggestions and comments which have led to a much improved paper. This work was supported by the National Natural Science Foundation of China under Grants 61273021, 60974132, 11172247, and 51208538 and in part by the Natural Science Foundation Project of CQ cstc2013jjB40008.

References

1 Yang X., Cao J., and Lu J., Synchronization of markovian coupled neural networks with nonidentical node-delays and random coupling strengths, IEEE Transactions on Neural Networks and Learning Systems. (2012) 23, no. 1, 60–71.
10.1109/TNNLS.2011.2177671
CAS PubMed Web of Science® Google Scholar
2 Chen T., Lu W., and Chen G., Dynamical behaviors of a large class of general delayed neural networks, Neural Computation. (2005) 17, no. 4, 949–968, https://doi.org/10.1162/0899766053429417, MR2175137, ZBL1080.68615.
10.1162/0899766053429417
Web of Science® Google Scholar
3 Cao J. and Song Q., Stability in Cohen-Grossberg-type bidirectional associative memory neural networks with time-varying delays, Nonlinearity. (2006) 19, no. 7, 1601–1617, https://doi.org/10.1088/0951-7715/19/7/008, MR2229792, ZBL1118.37038.
10.1088/0951-7715/19/7/008
Web of Science® Google Scholar
4 Zeng Z. and Zheng W., Multistability of neural networks with time-varying delays and concave-convex characteristics, IEEE Transactions on Neural Networks and Learning Systems. (2012) 23, no. 2, 293–305.
10.1109/TNNLS.2011.2179311
PubMed Web of Science® Google Scholar
5 Zhang H., Yang F., Liu X., and Zhang Q., Stability analysis for neural networks with time-varying delay based on quadratic convex combination, IEEE Transactions on Neural Networks and Learning Systems. (2013) 24, no. 2, 513–521.
10.1109/TNNLS.2012.2236571
PubMed Web of Science® Google Scholar
6 Jin L., Nikiforuk P. N., and Gupta M. M., Adaptive control of discrete-time nonlinear systems using recurrent neural networks, IEE Proceedings. (1994) 141, no. 3, 169–176, 2-s2.0-0028422937, https://doi.org/10.1049/ip-cta:19949976.
10.1049/ip-cta:19949976
Google Scholar
7 Wang Z., Ho D. W. C., and Liu X., State estimation for delayed neural networks, IEEE Transactions on Neural Networks. (2005) 16, no. 1, 279–284, 2-s2.0-13844256695, https://doi.org/10.1109/TNN.2004.841813.
10.1109/TNN.2004.841813
CAS PubMed Web of Science® Google Scholar
8 He Y., Wang Q., Wu M., and Lin C., Delay-dependent state estimation for delayed neural networks, IEEE Transactions on Neural Networks. (2006) 17, no. 4, 1077–1081, 2-s2.0-33746913856, https://doi.org/10.1109/TNN.2006.875969.
10.1109/TNN.2006.875969
PubMed Web of Science® Google Scholar
9 Li T. and Fei S., Exponential state estimation for recurrent neural networks with distributed delays, Neurocomputing. (2007) 71, no. 1–3, 428–438, 2-s2.0-35648996356, https://doi.org/10.1016/j.neucom.2007.07.005.
10.1016/j.neucom.2007.07.005
Web of Science® Google Scholar
10 Wang Z., Liu Y., and Liu X., State estimation for discrete-time Markovian jumping neural networks with mixed mode-dependent delays, Physics Letters A. (2008) 372, no. 48, 7147–7155, https://doi.org/10.1016/j.physleta.2008.10.045, MR2474610, ZBL1227.92002.
10.1016/j.physleta.2008.10.045
Web of Science® Google Scholar
11 Mou S., Gao H., Qiang W., and Fei Z., State estimation for discrete-time neural networks with time-varying delays, Neurocomputing. (2008) 72, no. 1–3, 643–647, 2-s2.0-55949130821, https://doi.org/10.1016/j.neucom.2008.06.009.
10.1016/j.neucom.2008.06.009
Web of Science® Google Scholar
12 Park J. H., Kwon O. M., and Lee S. M., State estimation for neural networks of neutral-type with interval time-varying delays, Applied Mathematics and Computation. (2008) 203, no. 1, 217–223, https://doi.org/10.1016/j.amc.2008.04.025, MR2451557, ZBL1166.34331.
10.1016/j.amc.2008.04.025
Web of Science® Google Scholar
13 Huang H., Feng G., and Cao J., Robust state estimation for uncertain neural networks with time-varying delay, IEEE Transactions on Neural Networks. (2008) 19, no. 8, 1329–1339, 2-s2.0-49649115035, https://doi.org/10.1109/TNN.2008.2000206.
10.1109/TNN.2008.2000206
PubMed Web of Science® Google Scholar
14 Mahmoud M. S., New exponentially convergent state estimation method for delayed neural networks, Neurocomputing. (2009) 72, no. 16–18, 3935–3942, 2-s2.0-69249246972, https://doi.org/10.1016/j.neucom.2009.04.007.
10.1016/j.neucom.2009.04.007
Web of Science® Google Scholar
15 Liu Y., Wang Z., and Liu X., State estimation for jumping recurrent neural networks with discrete and distributed delays, Neural Networks. (2009) 22, no. 1, 41–48, 2-s2.0-58249092623, https://doi.org/10.1016/j.neunet.2008.09.015.
10.1016/j.neunet.2008.09.015
PubMed Web of Science® Google Scholar
16 Park J. H. and Kwon O. M., Further results on state estimation for neural networks of neutral-type with time-varying delay, Applied Mathematics and Computation. (2009) 208, no. 1, 69–75, https://doi.org/10.1016/j.amc.2008.11.017, MR2490770, ZBL1169.34334.
10.1016/j.amc.2008.11.017
Web of Science® Google Scholar
17 Huang H., Feng G., and Cao J., State estimation for static neural networks with time-varying delay, Neural Networks. (2010) 23, no. 10, 1202–1207, 2-s2.0-78149500802, https://doi.org/10.1016/j.neunet.2010.07.001.
10.1016/j.neunet.2010.07.001
PubMed Web of Science® Google Scholar
18 Wang Z., Liu Y., Liu X., and Shi Y., Robust state estimation for discrete-time stochastic neural networks with probabilistic measurement delays, Neurocomputing. (2010) 74, no. 1–3, 256–264, 2-s2.0-78649460673, https://doi.org/10.1016/j.neucom.2010.03.013.
10.1016/j.neucom.2010.03.013
Web of Science® Google Scholar
19 Ahn C. K., Delay-dependent state estimation of T-S fuzzy delayed Hopfield neural networks, Nonlinear Dynamics. (2010) 61, no. 3, 483–489, https://doi.org/10.1007/s11071-010-9664-z, MR2718308.
10.1007/s11071-010-9664-z
Web of Science® Google Scholar
20 Wu Z., Su H., and Chu J., State estimation for discrete Markovian jumping neural networks with time delay, Neurocomputing. (2010) 73, no. 10–12, 2247–2254, 2-s2.0-77952548411, https://doi.org/10.1016/j.neucom.2010.01.010.
10.1016/j.neucom.2010.01.010
Web of Science® Google Scholar
21 Balasubramaniam P., Lakshmanan S., and Theesar S. J. S., State estimation for Markovian jumping recurrent neural networks with interval time-varying delays, Nonlinear Dynamics. (2010) 60, no. 4, 661–675, https://doi.org/10.1007/s11071-009-9623-8, MR2658541, ZBL1194.62109.
10.1007/s11071-009-9623-8
Web of Science® Google Scholar
22 Wang H. and Song Q., State estimation for neural networks with mixed interval time-varying delays, Neurocomputing. (2010) 73, no. 7–9, 1281–1288, 2-s2.0-77649233054, https://doi.org/10.1016/j.neucom.2009.12.017.
10.1016/j.neucom.2009.12.017
Web of Science® Google Scholar
23 Huang H. and Feng G., A scaling parameter approach to delay-dependent state estimation of delayed neural networks, IEEE Transactions on Circuits and Systems II. (2010) 57, no. 1, 36–40, 2-s2.0-76149137195, https://doi.org/10.1109/TCSII.2009.2035271.
10.1109/TCSII.2009.2035271
Web of Science® Google Scholar
24 Li X. and Rakkiyappan R., Robust asymptotic state estimation of Takagi-Sugeno fuzzy Markovian jumping Hopfield neural networks with mixed interval time-varying delays, Mathematical Methods in the Applied Sciences. (2011) 34, no. 17, 2197–2207, https://doi.org/10.1002/mma.1522, MR2861763, ZBL1233.34031.
10.1002/mma.1522
Web of Science® Google Scholar
25 Balasubramaniam P., Kalpana M., and Rakkiyappan R., State estimation for fuzzy cellular neural networks with time delay in the leakage term, discrete and unbounded distributed delays, Computers & Mathematics with Applications. (2011) 62, no. 10, 3959–3972, https://doi.org/10.1016/j.camwa.2011.09.048, MR2852113, ZBL1236.93004.
10.1016/j.camwa.2011.09.048
Web of Science® Google Scholar
26 Balasubramaniam P., Vembarasan V., and Rakkiyappan R., Delay-dependent robust exponential state estimation of Markovian jumping fuzzy Hopfield neural networks with mixed random time-varying delays, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 4, 2109–2129, https://doi.org/10.1016/j.cnsns.2010.08.024, MR2736076, ZBL1221.93254.
10.1016/j.cnsns.2010.08.024
Web of Science® Google Scholar
27 Bao H. and Cao J., Delay-distribution-dependent state estimation for discrete-time stochastic neural networks with random delay, Neural Networks. (2011) 24, no. 1, 19–28, 2-s2.0-78649670282, https://doi.org/10.1016/j.neunet.2010.09.010.
10.1016/j.neunet.2010.09.010
PubMed Web of Science® Google Scholar
28 Zhang D. and Yu L., Exponential state estimation for Markovian jumping neural networks with time-varying discrete and distributed delays, Neural Networks. (2012) 35, 103–111.
10.1016/j.neunet.2012.08.005
PubMed Web of Science® Google Scholar
29 Lakshmanan S., Park J. H., Ji D. H., Jung H. Y., and Nagamani G., State estimation of neural networks with time-varying delays and Markovian jumping parameter based on passivity theory, Nonlinear Dynamics. (2012) 70, no. 2, 1421–1434, https://doi.org/10.1007/s11071-012-0544-6, MR2992146, ZBL1268.92012.
10.1007/s11071-012-0544-6
Web of Science® Google Scholar
30 Chen Y. and Zheng W. X., Stochastic state estimation for neural networks with distributed delays and Markovian jump, Neural Networks. (2012) 25, 14–20, 2-s2.0-82355169632, https://doi.org/10.1016/j.neunet.2011.08.002.
10.1016/j.neunet.2011.08.002
PubMed Web of Science® Google Scholar
31 Kan X., Wang Z., and Shu H., State estimation for discrete-time delayed neural networks with fractional uncertainties and sensor saturations, Neurocomputing. (2013) 117, 64–71.
10.1016/j.neucom.2013.01.039
Web of Science® Google Scholar
32 Lee T. H., Park J. H., Kwon O. M., and Lee S. M., Stochastic sampled-data control for state estimation of time-varying delayed neural networks, Neural Networks. (2013) 46, 99–108.
10.1016/j.neunet.2013.05.001
PubMed Web of Science® Google Scholar
33 Ahn C. K., State estimation for T-S fuzzy Hopfield neural networks via strict output passivation of the error system, International Journal of General Systems. (2013) 42, no. 5, 503–518, MR3043237, https://doi.org/10.1080/03081079.2013.780052.
10.1080/03081079.2013.780052
Web of Science® Google Scholar
34 Huang H., Huang T., and Chen X., Guaranteed H_∞ performance state estimation of delayed static neural networks, IEEE Transactions on Circuits and Systems II. (2013) 60, no. 6, 371–375, https://doi.org/10.1109/TCSII.2013.2258258.
10.1109/TCSII.2013.2258258
Web of Science® Google Scholar
35 Lakshmanan S., Vembarasan V., and Balasubramaniam P., Delay decomposition approach to state estimation of neural networks with mixed time-varying delays and Markovian jumping parameters, Mathematical Methods in the Applied Sciences. (2013) 36, no. 4, 395–412, https://doi.org/10.1002/mma.2597, MR3032353, ZBL06163080.
10.1002/mma.2597
Web of Science® Google Scholar
36 Liang J., Wang Z., Shen B., and Liu X., Distributed state estimation in sensor networks with randomly occurring nonlinearities subject to time-delays, ACM Transactions on Sensor Networks. (2012) 9, no. 1, article 4.
10.1145/2379799.2379803
Web of Science® Google Scholar
37 Liang J., Wang Z., and Liu X., Distributed state estimation for uncertain Markov-type sensor networks with mode-dependent distributed delays, International Journal of Robust and Nonlinear Control. (2012) 22, no. 3, 331–346, https://doi.org/10.1002/rnc.1699, MR2880996, ZBL1261.93076.
10.1002/rnc.1699
Web of Science® Google Scholar
38 Liang J., Wang Z., and Liu X., Distributed state estimation for discrete-time sensor networks with randomly varying nonlinearities and missing measurements, IEEE Transactions on Neural Networks. (2011) 22, no. 3, 486–496.
10.1109/TNN.2011.2105501
PubMed Web of Science® Google Scholar
39 Gopalsamy K., Leakage delays in BAM, Journal of Mathematical Analysis and Applications. (2007) 325, no. 2, 1117–1132, https://doi.org/10.1016/j.jmaa.2006.02.039, MR2270073, ZBL1116.34058.
10.1016/j.jmaa.2006.02.039
Web of Science® Google Scholar
40 Liu Y., Wang Z., and Liu X., Global exponential stability of generalized recurrent neural networks with discrete and distributed delays, Neural Networks. (2006) 19, no. 5, 667–675, 2-s2.0-33646511197, https://doi.org/10.1016/j.neunet.2005.03.015.
10.1016/j.neunet.2005.03.015
PubMed Web of Science® Google Scholar

Citing Literature

All articles

State Estimation for Neural Networks with Leakage Delay and Time-Varying Delays

Abstract

1. Introduction

2. Model Description and Preliminaries

3. Main Results

4. Numerical Example

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

State Estimation for Neural Networks with Leakage Delay and Time-Varying Delays

Abstract

1. Introduction

2. Model Description and Preliminaries

3. Main Results

4. Numerical Example

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information