We introduce a time-to-build technology in a Solow model with nonconstant population. Our analysis shows that the population dynamics may be a source of stability switches and Hopf bifurcations. The analytical results are obtained using the recent technique introduced by Beretta and Kuang (2002) in the studying of delayed differential equations with delay-dependent coefficients in characteristic equation. Numerical simulations are performed in order to illustrate the main dynamic features of the model.

1. Introduction

The relationship between economic activity and population dynamics is a multifaceted issue. On the one hand, demographic changes affect many economic variables such as labour force [1] or public spending for pension system [2–4]; on the other hand, macroeconomic environment may influence fertility choices [5–7], life time expectation [8, 9], and emigration and immigration decisions [10].

Taking into account these aspects, many authors have built models in which nonlinear mechanisms are sources of oscillating trajectories of the main demoeconomic variables. Day at al. [11] show the possibility of chaotic dynamics in a discrete overlapping generations model in which agents are assumed to determine the number of children in a trade-off between the cost of childbearing and private consumption; Feichtinger and Sorger [12] introduce, according to Easterlin theory, some feedback mechanisms into population dynamics able to generate oscillating birth trajectories; Benhabib and Nishimura [13] and Feichtinger and Sorger [12] show the existence of nonlinear dynamics in neoclassical models of fertility; Manfredi and Fanti [14, 15] study the occurrence of limit cycles or complex behaviours in Goodwin-type models in which the dynamics of the population of workers is introduced; Fanti and Gori [16] study the possibility of cyclical instability in an overlapping generations model with pay-as-you-go pension scheme.

In this paper we analyze another source of endogenous fluctuations in demoeconomic variables. In particular we focus on the relation between neoclassical production, population dynamics, and stability of equilibrium path using a Solow-type framework in which population evolves at a constant (positive or negative) rate and a time-to-build technology is introduced. From a theoretical point of view, it is interesting to note that in standard versions of the Solow and Ramsey models without delays but with a positive rate of population growth, because of the assumption of constant returns to scale, (i) the size of population does not influence the long run growth rate of the economy (this property is not shared by many endogenous growth models à la Romer that suffer from an unrealistic scale effect (see the criticism and the alternative approach proposed by Jones [26] who studies a model with results really similar to the Solow model)); (ii) the rate of growth of population determines the long run rate of capital accumulation to which the economy converges; (iii) there exists a unique globally attracting equilibrium, and trajectories converge monotonically to it (see [17, 18]). Instead, if population is decreasing and the interior equilibrium acts as a watershed for the trajectories of the model and the ratio of capital to labour and according to initial conditions may converge to zero or be divergent. Nevertheless, in all cited works, it is worthy to note that the time series seems to be too regular in order to describe the real evolutions of economic variables.

Instead, if temporal lags in the production of capital goods are introduced and the rate of growth of population is different from zero, the dynamical system that describes the time evolution of per capita physical capital and the associated characteristic equation involve delay-dependent coefficients. In this case, the results are really different with respect to models (e.g., [19–22]) with fixed population size (and then with delay independent parameters). In particular stability switches as well as Hopf bifurcations may arise for realistic values of time delay.

From an analytical point of view, in order to characterize the local dynamics of the system, we will use the recent approach introduced by Beretta and Kuang [23] and based on the existence of real zeros of particular functions S_j(τ). We will show that if n ≠ 0 then the system is able to produce stability switches and Hopf bifurcations when time delay varies. The paper is organised as follows. Section 2 presents the model. Section 3 studies the dynamic phenomena; Section 4 concludes the paper.

2. The Model

We consider a growth model à la Solow [24] in which there exists a delay of τ periods before capital becomes productive after the investment. This implies that, at time t, the productive capital stock is K(t − τ). By assuming a Cobb-Douglas technology, we have that the total income at time t is Y(t) = K(t − τ) ^αL(t) ^1−α, where L(t) represents labor force at time t and α ∈ (0,1) is the capital’s share. Departing from Zak [22] we assume that population grows at a constant rate n ≠ 0. Let s ∈ (0,1) be the constant saving rate and δ ∈ (0,1) the constant proportion of the capital stock that depreciates during production. From the identities Y(t) = C(t) + I(t) + δK(t) and I(t) = S(t), where C(t), S(t), and I(t) are consumption, saving, and investment, respectively, all evaluated at time t, it follows that the equation of capital accumulation is

()

In order to simplify the notation we omit the indication of time dependence for variables and derivatives referred at time t, and we use x_d to indicate the state of the variable x at time t − τ. Setting k = K/L, the evolution of per capita physical capital over time is given by

()

Normalizing the number of people at time zero to one yields L = e^nt. Then, substituting this in the above equation, we derive that our model is described by the following delay differential equation with delay-dependent coefficients

()

The equilibria of (3) are obtained by setting

and k_d = k = k_* for all t. Doing this, one finds that the nontrivial equilibria k_* of (3) must satisfy

()

Lemma 1. For every τ ≥ 0, there exist a unique positive equilibrium if n > 0 and a unique positive equilibrium if n < 0 and δ + n > 0.

Using Taylor expansion on the right-hand side of (3) around

, we get the linearized equation

()

From this, we obtain the characteristic equation

()

Equation (6) is a transcendental equation which has an infinite number of complex roots. For τ = 0, the characteristic equation (6) becomes λ = (α − 1)(δ + n) < 0. Therefore, the equilibrium point

is locally asymptotically stable. We have discussed (3) in the absence of delay. In the next section, we will investigate our model when delay is present and try to analyze the effect of the gestation time lag.

3. Stability and Existence of Hopf Bifurcation

Now we assume τ > 0 and regard it as a bifurcation parameter to obtain results on the stability of

. It is well known that the change of stability of

will occur for Re(λ) = 0. First, λ = 0 is not a root of the characteristic equation (6). Otherwise, we would have D(0, τ) = n + (1 − α)δe^−nτ − αn = 0, yielding the absurd −n = δe^−nτ. Second, we note that (6) takes the form of an exponential polynomial with a coefficient depending on τ. Thus, we use the method introduced by Beretta and Kuang [23], which gives the existence of purely imaginary roots of a characteristic equation with delay-dependent coefficients. To find out the position of change of stability we substitute λ = iω (ω = ω(τ) > 0) in (6) and then separating the real and imaginary parts we get

()

By taking square of both sides of system (7) and then adding them up, one obtains the following equation:

()

Lemma 2. Let n ≠ 0. Then (8) has a positive root given by

()

only if the following condition holds:

()

Proof. Solving (8) for ω leads to (9), which is well defined if |(1 − α)δe^−nτ − αn| > |n|. When n > 0, this means |(1 − α)δe^−nτ − αn| > n; that is, (1 − α)δe^−nτ − αn < −n and (1 − α)δe^−nτ − αn > n. The first of these two inequalities yields 0 < δe^−nτ < −n < 0. Let n < 0. Then the above condition reduces to (1 − α)δe^−nτ − αn > −n. The conclusion follows.

Corollary 3. (1) Let n < 0. Then condition (10) is equivalent to τ > 0.

(2) Let n > 0. Then condition (10) is equivalent to

()

Proof. Let n < 0. Then (10) is (1 − α)δe^−nτ − αn > −n. Hence, we get δe^−nτ > −n, which is always satisfied being δ + n > 0 in this case. Let n > 0. Then (10) becomes (1 − α)δe^−nτ − αn > n. A direct calculation yields the statement.

Define

()

with

()

Note that τ_c > 0 since the logarithm argument is greater than one. According to Beretta and Kuang’s [23] procedure, we now substitute (9) into system (7) and define the angle θ(τ)∈(π/2, π) for τ ∈ Γ as solution of

()

A necessary and sufficient condition for λ = ±iω(τ), ω(τ) > 0 solution of (8), to be characteristic roots of (6) is that the arguments ω(τ)τ in system (7) and θ(τ) in system (14) are in the relationship

()

Then, we can define the functions

()

whose explicit expressions can be obtained from (14) as follows:

()

Therefore, λ = ±iω(τ), ω(τ) > 0, is a purely imaginary root of (6) if and only if τ is a zero of the functions S_j, where

()

Proposition 4. The characteristic equation (6) has a pair of simple pure imaginary roots λ = ±iω_*, ω_* = ω(τ_*) > 0, at τ_* ∈ Γ, provided S_j(τ_*) = 0 for some j ∈ ℕ⁰. Moreover, this pair of simple conjugate purely imaginary roots crosses the imaginary axis from left to right if Λ(τ_*) > 0 and crosses the imaginary axis from right to left if Λ(τ_*) < 0, where

()

Proof. First, we prove that λ = iω_* is a simple root of (6). If λ = iω_* is a repeated root, then D(iω_*, τ_*) = D^′(iω_*, τ_*) = 0 holds true, leading to 1 + (iω_* + n)τ_* = 0, which is a contradiction. Differentiating (6) with respect to τ, we find

()

Using (6) and (8), one has

()

Noticing that (8) yields

()

the above rewrites as

()

Hence,

()

Differentiating (18) with respect to τ and using (17), it follows

()

Since S_j(τ_*) = 0 gives τ_j(τ_*) = τ_*, comparing (25) evaluated at τ = τ_* with (24), the conclusion holds.

We can easily observe the following properties of S_j(τ), τ ∈ Γ.

(1)
S_j(τ) > S_j+1(τ), for τ ∈ Γ and j ∈ ℕ₀. Therefore, S_j has no zeros in Γ for any j ∈ ℕ₀ if S₀ has no zeros in Γ.
(2)
From (9), we have ω(0) > 0. Hence, S₀(0) < 0.
(3)
As , ω(τ) → 0, we derive S₀(τ)→−∞ as .
(4)
As τ → +∞, ω(τ)→+∞, we get S₀(τ)→+∞ as τ → +∞.

Without loss of generality, we may suppose that if S_j(τ) has positive zeros, then dS_j(τ)/dτ ≠ 0 at these points; that is, the zeros are simple. Applying Hopf bifurcation theorem for functional differential equations (see Hale’s book [25]), we can conclude the existence of a Hopf bifurcation.

Summing up all the above analysis, we can state the main results in the next two Theorems.

Theorem 5. Let n < 0.

(i)
A stability switch always exists in (0, +∞) since the function S₀(τ) has at least one positive simple zero in (0, +∞).
(ii)
The function S_j(τ) has a finite number of positive simple zeros in (0, +∞), for any j ∈ ℕ₀ and the number of these roots is odd; say τ₁, τ₂, …, τ_2N+1 (τ₁ < τ₂ < ⋯<τ_2N+1), respectively.
- (ii₁)
  Equation (3) undergoes a Hopf bifurcation at the equilibrium k_* when τ = τ_r, r = 1,2, …, 2N + 1.
- (ii₂)
  k_* is locally asymptotically stable for τ ∈ [0, τ₁)∪(τ_2l, τ_2l+1) (l = 0,1, 2, …, N; τ₀ = 0) and unstable if τ ∈ (τ_2l+1, τ_2l+2) (l = 0,1, 2, …, N; τ_2N+2 = +∞).

Theorem 6. Let n > 0.

(i)
If α ≥ (δ − n)/(δ + n) holds or if α < (δ − n)/(δ + n) and the function S₀(τ) has no positive simple zeros in (0, τ_c), then the equilibrium k_* is locally asymptotically stable for all τ ∈ [0, τ_c).
(ii)
If α < (δ − n)/(δ + n) holds, then the function S_j(τ) has a finite number of positive simple zeros in (0, τ_c), for any fixed j ∈ ℕ₀ and the number of these roots is even; say τ₁, τ₂, …, τ_2N (τ₁ < τ₂ < ⋯<τ_2N), respectively.
- (ii₁)
  Equation (3) undergoes a Hopf bifurcation at the equilibrium k_* when τ = τ_r, r = 1,2, …, 2N.
- (ii₂)
  k_* is locally asymptotically stable for τ ∈ [0, τ₁)∪(τ_2l, τ_2l+1) (l = 0,1, 2, …, N; τ₀ = 0 and τ_2N+1 = τ_c) and unstable if τ ∈ (τ_2l+1, τ_2l+2) (l = 0,1, 2, …, N − 1).

In order to clarify the interesting dynamic properties of the system stated in Theorems 5 and 6 we now resort to some numerical experiments by taking the following configurations of parameters:

()

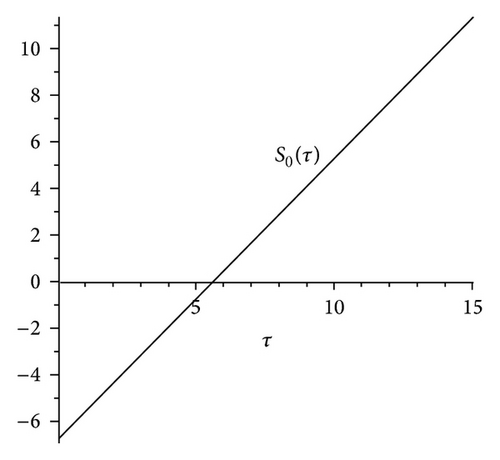
In the whole section τ may be interpreted as the number of months before capital can be used for production. We first consider (26). Figure 1 shows the existence of a unique zero for S₀, τ₁≅5.463. According to Theorem 5 the equilibrium is locally asymptotically stable for τ < τ₁ and undergoes a Hopf bifurcation for τ = τ₁. Just after this value a closed invariant curve exists. For large enough value of time delay no feasible trajectories exist.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

(a) Graph of stability switch in terms of time delay if n < 0 (parameter specification (26)); (b) associated bifurcation diagram; (c) phase plane for τ = 5; and (d) phase plane for τ = 5.6.

We now consider (27). If α is large enough (α > 0.791) we are in case (i) of Theorem 6 and no zero for S₀ exists and the equilibrium is locally asymptotically stable. Numerically we verify that no zero exists until α > α_tr, where α_tr≅0.255 is the value of alpha such that S₀ is tangent to horizontal axis (see Figure 2(a)).

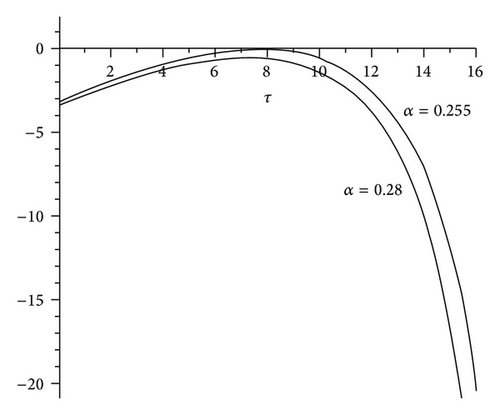
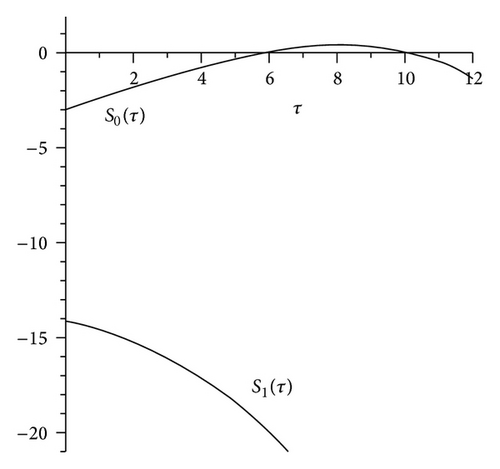
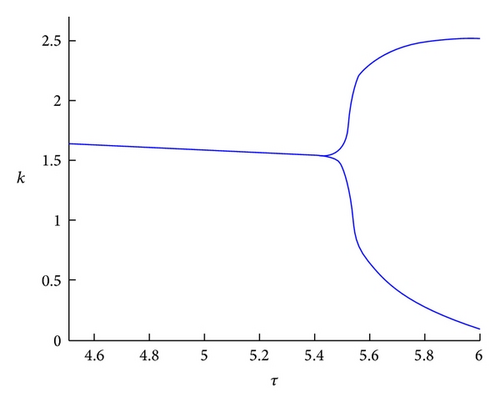
For α ∈ (0, α_tr) S₀ has two positive zeros. We set α = 0.23 (see Figure 2(b)). The zeros of S₀ are τ₁≅5.7812 and τ₂ = τ_N≅10.234.

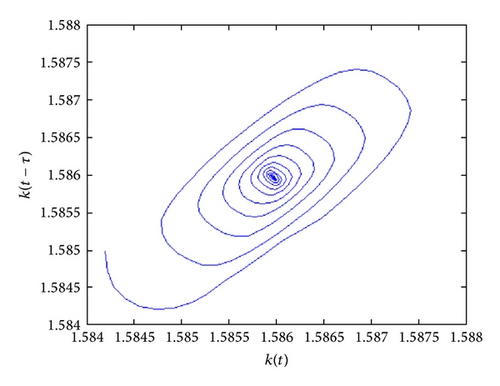
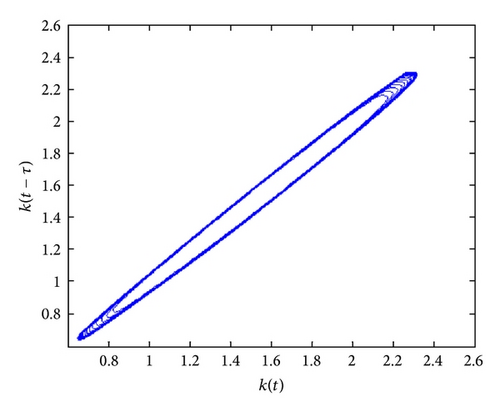
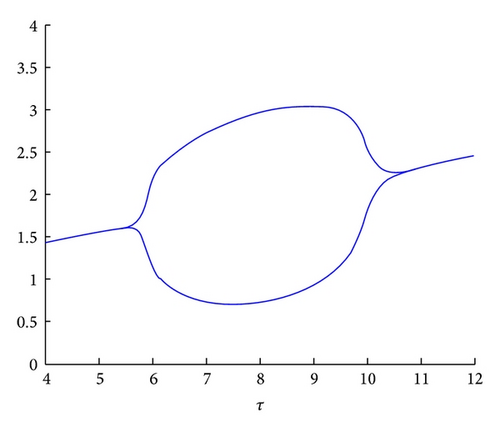
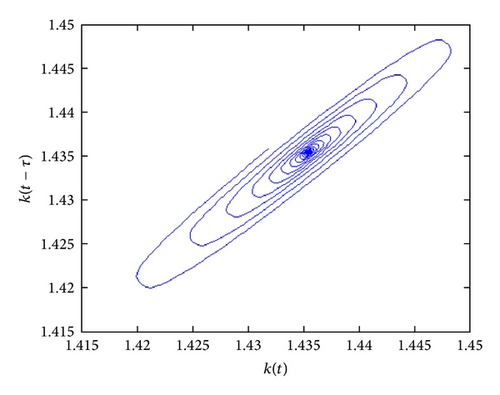
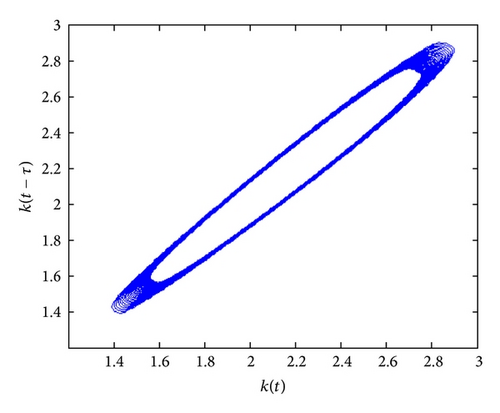
According to case (ii) in Theorem 6, we have that, for all τ ∈ (0,5.7812), the equilibrium is stable; for τ = 5.7812 the equilibrium undergoes a supercritical Hopf bifurcation and for τ ∈ (5.7812,10.234) a closed curve captures trajectories starting close enough to the unstable equilibrium; finally, for τ = 12.653 equilibrium undergoes a second Hopf bifurcation and the equilibrium becomes stable again (see the set of Figure 3). No other bifurcation occurs for larger values of τ.

4. Conclusions

In this paper we have presented a theoretical explanation of economic cycles due to demographic reasons. Our model makes use of the Solow model with exogenous saving rate, exogenous population growth, and time-to-build technology. The economic and demographic variables are related through production function. The model proposed in this paper has several features that distinguish it from other approaches to nonlinear evolution of demoeconomic variables. Different from some contributions on the topic (see, e.g., [1]), we do not introduce ad hoc feedback mechanisms in order to describe non linear phenomena. Furthermore, we do not model other sources of nonlinearities such as the age structure (see [12]) of population or behavioural assumptions on fertility rate or optimizing decisions on the number of children (see [13]). Nonetheless, comparable results in terms of dynamical properties are obtained. Thus, we can conclude that the existence of persistent cycles seems to be a quite general result because it relays on the coexistence of capital and nonconstant labour in production of goods. From a mathematical point of view, we have shown that the introduction of population dynamics drastically changes the results of the model with respect to the case n = 0 (see [22]). If n ≠ 0, the system is able to produce stability switches and Hopf bifurcations when time delay varies not observable for n = 0. In particular we have seen that when n < 0, time delay may play a destabilising role for intermediate values of the parameter and eventually it may stabilise.

References

1 Fanti L. and Manfredi P., Population, unemployment and economic growth cycles: a further explanatory perspective, Metroeconomica. (2003) 54, no. 2-3, 179–207, https://doi.org/10.1111/1467-999X.00165, MR2006109, ZBL1069.91074.
10.1111/1467-999X.00165
Google Scholar
2 van Groezen B. and Meijdam L., Growing old and staying young: population policy in an ageing closed economy, Journal of Population Economics. (2008) 21, no. 3, 573–588.
10.1007/s00148-006-0067-x
Web of Science® Google Scholar
3 van Groezen B., Leers T., and Meijdam L., Social security and endogenous fertility: pensions and child allowances as siamese twins, Journal of Population Economics. (2003) 87, no. 2, 233–251.
Google Scholar
4 Pecchenino R. A. and Pollard P. S., Aging, myopia, and the pay-as-you-go public pension systems of the G7: a bright future?, Journal of Public Economic Theory. (2005) 7, no. 3, 449–470.
10.1111/j.1467-9779.2005.00212.x
Google Scholar
5 Barro R. J. and Becker G. S., Fertility choice in a model of economic growth, Econometrica. (1989) 57, 481–501.
10.2307/1912563
Web of Science® Google Scholar
6 Becker G. S., NBER, An economic analysis of fertility, Demographic and Economic Change in Developed Countries, 1960, Princeton University Press, Princeton, NJ, USA.
Google Scholar
7 Becker G., Murphy K. M., and Tamura R., Human capital, fertility and economic growth, Journal of Political Economy, 1990, 98, 12–37.
10.3386/w3414
Google Scholar
8 Blackburn K. and Cipriani G. P., A model of longevity, fertility and growth, Journal of Economic Dynamics and Control. (2002) 26, 187–204.
10.1016/S0165-1889(00)00022-1
Web of Science® Google Scholar
9 Chakraborty S., Endogenous lifetime and economic growth, Journal of Economic Theory. (2004) 116, no. 1, 119–137, https://doi.org/10.1016/j.jet.2003.07.005, MR2048436, ZBL1070.91048.
10.1016/j.jet.2003.07.005
Web of Science® Google Scholar
10 Sanso M. and Larramona G., Migration dynamics, growth and convergence, Journal of Economic Dynamics & Control. (2006) 30, 2261–2279.
10.1016/j.jedc.2005.06.015
Web of Science® Google Scholar
11 Day R. H., Kim K. H., and Macunovich D., Complex demoeconomic dynamics, Journal of Population Economics. (1989) 2159, no. 2.
Google Scholar
12 Feichtinger G. and Sorger G., Self-generating fertility waves in a nonlinear continuous overlapping generations model, Journal of Population Economics. (1989) 2, 267–280.
10.1007/BF00171004
CAS PubMed Google Scholar
13 Benhabib J. and Nishimura K., A. Wenig and K. F. Zimmermann, Endogenous uctuations in the Barro-Becker theory of fertility, Demographic Change and Economic Development, 1989, 41, Springer, Berlin, Germany, 29–41.
10.1007/978-3-642-83789-0_2
Google Scholar
14 Manfredi P. and Fanti L., The complex effects of the interaction between the economy and population, Structural Change and Economic Dynamics. (2006) 17, 148–173.
10.1016/j.strueco.2004.12.003
Google Scholar
15 Manfredi P. and Fanti L., Demography in macroeconomic models: when labour supply matters for economic cycles, Metroeconomica. (2006) 57, no. 4, 536–563.
10.1111/j.1467-999X.2006.00255.x
Google Scholar
16 Fanti L. and Gori L., Fertility-related pensions and cyclical instability, Journal of Population Economics. (2013) 26, no. 3, 1209–1232.
10.1007/s00148-012-0462-4
Web of Science® Google Scholar
17 Bucci A. and Guerrini L., Transitional dynamics in the Solow-Swan growth model with AK technology and logistic population change, B.E. Journal of Macroeconomics. (2009) 916, no. 1.
Google Scholar
18 Guerrini L., The Solow-Swan model with a bounded population growth rate, Journal of Mathematical Economics. (2006) 42, no. 1, 14–21, https://doi.org/10.1016/j.jmateco.2005.05.001, MR2205647, ZBL1142.91663.
10.1016/j.jmateco.2005.05.001
Web of Science® Google Scholar
19 Bianca C., Ferrara M., and Guerrini L., Hopf bifurcations in a delayed-energy-based model of capital accumulation, Applied Mathematics & Information Sciences. (2013) 7, no. 1, 139–143, https://doi.org/10.12785/amis/070116, MR2998494.
10.12785/amis/070116
Google Scholar
20 Bianca C., Ferrara M., and Guerrini L., The Cai model with time delay: existence of periodic solutions and asymptotic analysis, Applied Mathematics & Information Sciences. (2013) 7, no. 1, 21–27, https://doi.org/10.12785/amis/070103, MR2998481.
10.12785/amis/070103
Google Scholar
21 Bianca C. and Guerrini L., On the dalgaard-strulik model with logistic population growth rate and delayed-carrying capacity, Acta Applicandae Mathematicae. (2013) 128, 39–48, https://doi.org/10.1007/s10440-013-9800-0, MR3125634.
10.1007/s10440-013-9800-0
Web of Science® Google Scholar
22 Zak P. J., Kaleckian lags in general equilibrium, Review of Political Economy. (1999) 11, 321–330.
10.1080/095382599107048
Google Scholar
23 Beretta E. and Kuang Y., Geometric stability switch criteria in delay differential systems with delay dependent parameters, SIAM Journal on Mathematical Analysis. (2002) 33, no. 5, 1144–1165, https://doi.org/10.1137/S0036141000376086, MR1897706, ZBL1013.92034.
10.1137/S0036141000376086
Web of Science® Google Scholar
24 Solow R. M., A contribution to the theory of economic growth, Quarterly Journal of Economics. (1956) 70, 65–94.
10.2307/1884513
Web of Science® Google Scholar
25 Hale J. K. and Verduyn Lunel S. M., Introduction to Functional-Differential Equations, 1993, Springer, New York, NY, USA, MR1243878.
10.1007/978-1-4612-4342-7
Google Scholar
26 Jones C. I., R&D-based models of economic growth, Journal of Political Economy. (1995) 103, 759–784.
10.1086/262002
Web of Science® Google Scholar

Citing Literature

All articles

Dynamic Properties of the Solow Model with Increasing or Decreasing Population and Time-to-Build Technology

Abstract

1. Introduction

2. The Model

3. Stability and Existence of Hopf Bifurcation

4. Conclusions

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Dynamic Properties of the Solow Model with Increasing or Decreasing Population and Time-to-Build Technology

Abstract

1. Introduction

2. The Model

3. Stability and Existence of Hopf Bifurcation

4. Conclusions

References

Citing Literature

Figures

References

Related

Information