The nonfragile robust finite-time L₂-L_∞ control problem for a class of nonlinear uncertain systems with uncertainties and time-delays is considered. The nonlinear parameters are considered to satisfy the Lipschitz conditions and the exogenous disturbances are unknown but energy bounded. By using the Lyapunov function approach, the sufficient condition for the existence of nonfragile robust finite-time L₂-L_∞ controller is given in terms of linear matrix inequalities (LMIs). The finite-time controller is designed such that the resulting closed-loop system is finite-time bounded for all admissible uncertainties and satisfies the given L₂-L_∞ control index. Simulation results illustrate the validity of the proposed approach.

1. Introduction

Time-delay is frequently a source of instability and always encounters in various engineering systems such as chemical processes, neural networks, and long transmission lines in pneumatic systems. Recently, many attentions have been paid to the solutions of deal with time-delay which existed in concerned systems, such as the input-output technique [1], delay partitioning method [2], and piecewise analysis method [3]. As an important class of nonlinear systems, the Lipschitzian nonlinear system also has drawn considerable attention in the past few decades. Among these researches, the studies of Lipschitz nonlinear systems with time-delays have received much attention [4–6].

However, it is necessary to point out that the results of the aforementioned papers about time-delayed Lipschitz systems are mostly based on Lyapunov stable theory. As we all known, Lyapunov stable theory pays more attention to the asymptotic pattern of systems over an infinite-time interval. But in some practical process, the main attention may be related to the behavior of the dynamical systems over fixed finite-time interval; for instance, large values of the states cannot be accepted in the presence of saturations. To deal with such situations, Dorato [7] first presented the concept of finite-time stability (or short-time stability) in 1961. In [8], Amato et al. first proposed the concept of finite-time boundedness; thereafter many attempts on finite-time control problems have been made [9–13]. However, to date, little work has been paid attention in finite-time controller design for Lipschitzian nonlinear system. The research topic is still open but challenging. And this is the key motivation of this paper.

On the other hand, in the feedback control schemes, there are often some perturbations appeared in controller gain, which may result from either the actuator degradations or the requirements of readjustment of controller gains during the controller implementation stage. Therefore, it is reasonable that any controller should be able to tolerate some level of controller gain variations, and this motivates many researchers to study the nonfragile controller problems [14–19]. Motivated by the benefits of nonfragile state feedback controller, we consider the nonfragile controller design problem in this paper.

In addition, energy to peak (L₂-L_∞) control is of a great importance both in control theory and in engineering practice, because of its insensitivity to the exact knowledge of the statistics of the external disturbance signals. In [20], Rotea first introduced the L₂-L_∞ performance index. After that many researchers have paid attention in L₂-L_∞ control problems. For example, in [21], the authors studied the L₂-L_∞ controller design problem for continuous-time multiple delayed linear systems; in [22], the problem of L₂-L_∞ control for a class of uncertain singular systems with time-delay and norm-bounded parameter uncertainties was investigated by the researchers. For more details of the literatures related to L₂-L_∞ control schemes, the readers can refer to [21–24] and the references therein.

In short, to the best knowledge of authors, the problem of nonfragile robust finite-time L₂-L_∞ control for a class of uncertain Lipschitz nonlinear systems with time-delays is not studied at present. This motivates our research.

This paper deals with the problem of nonfragile robust finite-time L₂-L_∞ control for a class of Lipschitz nonlinear systems with time-delays and uncertainties, and the nonlinear function is assumed to satisfy the Lipschitz conditions. The uncertain parameters are assumed to be time varying and energy bounded. The purpose is to construct a nonfragile state feedback controller such that the resulting closed-loop system is finite-time bounded and satisfies the given L₂-L_∞ index. By using the Lyapunov function approach and linear matrix inequality techniques, a sufficient condition for the existence of a nonfragile state feedback controller is given and an explicit expression of this controller is presented. Meanwhile, this problem is reduced to an optimization problem under the constraint of LMIs. Finally, a simulation example illustrates the effectiveness of the developed techniques.

The paper is organized as follows. In Section 2, the system description along with necessary assumption is given. Section 3 provides the main results. A simulation example is provided to illustrate the results of the paper in Section 4. Conclusion follows in Section 5.

Notation 1. In the sequel, if not explicitly stated, matrices are assumed to have compatible dimensions. I and 0 represent the identity matrix and a zero matrix. The notation M > (≥, <, ≤) 0 is used to denote a symmetric positive-definite (positive semidefinite, negative-definite, negative semidefinite) matrix. λ_min(·), λ_max(·) denote the minimum and the maximum eigenvalue of the corresponding matrix, respectively. L₂[0 +∞) denotes the Euclidean norm for vectors or the spectral norm of matrices. is the space of n-dimensional square integrable function vector over [0 N]. In symmetric black matrices, we use * that represents the elements below the main diagonal of a symmetric block matrix. The superscript T represents the transpose.

2. Preliminaries and Problem Statement

Consider a class of Lipschitz nonlinear systems with time-delay and parameter uncertainties described by the following equations:

(1)

where x(t) ∈ ℜⁿ is the state, x(t − d) ∈ ℜⁿ is the constant time-delay state, u(t) ∈ ℜ^p is the controlled input, w(t) ∈ ℜ^r is the disturbance input that belongs to L₂[0 +∞),

is the nonlinear function which represents the known nonlinear disturbance related to the state and the time-delay state, and φ(t) ∈ L₂[−d 0] is a continuous vector-valued initial function. In addition, A, A_d, B, G, F, C, and D are known real matrices, and ΔA(t), ΔA_d(t), ΔG(t), ΔF(t), and ΔC(t) are unknown time-variant matrices representing the norm-bounded parameter uncertainties and satisfy the following form:

(2)

(3)

where M₁, M₂, S₁, S₂, S₃, and S₄ are known real constants matrices and Γ(t) is the time-varying unknown matrix function with Lebesgue norm measurable elements.

Remark 1. The parameter uncertainty structure as in (2) and (3) has been widely used in the existing literatures, such as [22, 24, 25]. In many practical applications, the systems parameter uncertainties can be either exactly modeled or overbounded by (3). Note that the unknown matrix function Γ(t) is time-varying, therefore it can be allowed to be state-dependent in some case, that is, Γ(t) = Γ(t, x(t)).

The following preliminary assumptions are made for system (1).

Assumption 1. For any given positive number δ and constant time T, the external disturbances input w(t) is time-varying and satisfies

(4)

Assumption 2. is a known nonlinear function which satisfies the following Lipschitz conditions:

(i)
f(0, 0) = 0;
(ii)
∥f(x(t), x(t − d))∥ ≤ ∥η₁x(t)∥ + ∥η₂x(t − d)∥,

where the weighting matrices η₁ and η₂ are known real constant matrices.

Remark 2. The above Lipschitz condition can be considered as an extension of the Lipschitz condition mentioned in [19]. When and , the Lipschitz condition in Assumption 2 will reduce to (4) [19].

Our aim is to develop a nonfragile state feedback controller:

(5)

where the matrix K is the controller gain to be determined and ΔK(t) is the controller gain variations. Here, we consider the additive controller gain variation, that is,

(6)

where H and N are known matrices, and ρ(t) is unknown but norm bounded.

Remark 3. The controller gain perturbations can result from the actuator degradations, as well as from the requirements for readjustment of controller gain during the controller implementation stage. Theses perturbations in the controller gains are modeled here as uncertain gains that are dependent on the uncertain parameters [6]. The models of additive uncertainties and multiplicative uncertainties are used to describe the controller gain variations. For more results on this topic, we refer readers to [6, 17, 18] and the references therein.

By the nonfragile state feedback controller (5), the closed-loop system can be obtained as follows:

(7)

where

To formulate the problem addressed in this paper, we give the following definitions first.

Definition 4 (FTB). For given constants c₁ > 0, δ > 0, and T > 0 and a symmetric matrix R > 0, the closed-loop system (7) is said to be robust finite-time bounded (FTB) with respect to (c₁ c₂ δ T R), if there exists a constant c₂ > c₁, such that the following relation holds for all the external disturbance w(t):

(8)

Remark 5. In fact, if the closed-loop system (7) does not exist the exogenous disturbance input, that is, w(t) = 0, the concept of FTB reduces to finite-time stable (FTS) [8, 11]. That is to say, a system is FTB, if given a bound initial condition and characterization of the set of admissible inputs, then the system states remain below the prescribed limit for all inputs in the bounded set.

Definition 6. The state-feedback controller (5) is said to be a nonfragile robust finite-time L₂-L_∞ controller with disturbance attenuation γ > 0 for system (1) if the closed-loop system (7) is FTB in the sense of Definition 4, and there exists a positive real constant γ > 0 such that

(9)

where

Furthermore, we introduce the following lemmas which will be used in the development of our main results.

Lemma 7 (see [26].)Let X and Y be real matrices of appropriate dimensions. For any given scalar ε > 0 and vectors x, y ∈ ℜⁿ, then

(10)

Lemma 8 (see [27].)Let M and N be real matrices of appropriate dimensions. Then for any matrix F(t) satisfying F^Τ(t)F(t) ≤ I and a scalar μ > 0,

(11)

3. Main Results

In this section, we will solve the problem of nonfragile robust finite-time L₂-L_∞ controller design for a class of Lipschitz uncertain nonlinear time-delay systems formulated in the previous section based on LMI approach. The following results actually present the FTB condition for closed-loop system (7) with time-delays.

Theorem 9. For given c₁ > 0, δ > 0, T > 0, ε > 0, α > 0 and weighting matrices η₁, η₂, R > 0, the closed-loop controlled system (7) is FTB with respect to (c₁ c₂ δ T R), if there exists constant c₂ > 0, symmetric positive- definite matrices P and , such that

(12)

(13)

where

Proof. Choose a Lyapunov function candidate V(x(t)) as

(14)

Along the trajectories of system (7), the corresponding time derivation of V(x(t)) is given by

(15)

Using Assumption 2, we have

(16)

Considering Lemma 7, we can obtain the following relation for any given scalar ε > 0

(17)

Hence, relation (15) can be rewritten as

(18)

Define the following function:

(19)

Considering (18) and (14), we obtain

(20)

where

According to α > 0 and Q > 0, inequality (20) implies J₁ < 0. Thus, by using (19), we get

(21)

Pre- and postmultiplying (20) by e^−αt, it yields

(22)

Integrating the aforementioned inequality between 0 and t, it follows that

(23)

Then, the above inequality is equivalent to

(24)

Noting that

, it follows from (14) that

(25)

On the other hand, the following condition holds:

(26)

Combining (24), (25), and (26), we can get

(27)

Recalling condition (13), it implies that for ∀t ∈ [0 T], x^T(t)Rx(t) < c₂. This completes the proof.

Remark 10. Without the time-delay in the resulted closed-loop system (7), the system will reduce to the system which has been investigated in [25, 28]. In this case, one can get the sufficient conditions of FTB for the aforementioned system from Theorem 9 via a simple transformation. Furthermore, if there is also no nonlinear function in the aforementioned system, then Theorem 9 reduces to a form which has been given in [8, Lemma 6] or [13, Lemma 1].

Theorem 9 gives the sufficient condition of FTB for the resulting closed-loop controlled system (7). Then, we will apply the results in Theorem 11 to solve the problem of nonfragile robust finite-time L₂-L_∞ controller design.

Theorem 11. For given c₁ > 0, δ > 0, T > 0, ε > 0, α > 0, and weighting matrices η₁, η₂, R > 0, the closed-loop system (7) is FTB with respect to (c₁ c₂ δ T R) and satisfies the cost function (9) for all admissible w(t) with the constraint condition and all admissible uncertainties, if there exist constants c₂ > 0, β > 0, symmetric positive-definite matrices P and , such that conditions (12), (13), and the following inequality hold:

(28)

Proof. Defining the same Lyapunov function as Theorem 9. Under the zero initial state condition φ(t) = 0, t ∈ [−d 0], we can rewrite (24) as

(29)

Hence, from (14) and ∀t ∈ [0 T], we can get

(30)

Furthermore, from (28) and using Schur complement, we have

(31)

Then, it follows

(32)

Taking the maximum value of , we have with t ∈ [0 T]. Therefore, condition (9) can be guaranteed by letting . This completes the proof.

In order to solve Theorem 11, we can obtain the relevant algorithm by imposing further LMI constraints in the design phase. Substituting the corresponding matrices into matrix inequalities (12), (13), and (28), we can draw the following Theorem 12.

Theorem 12. For given c₁ > 0, δ > 0, T > 0, ε > 0, α > 0, and weighting matrices η₁, η₂, R > 0, the closed-loop system (7) is FTB with respect to (c₁ c₂ δ T R), exists a nonfragile state-feedback controller gain K = YX⁻¹, and satisfies the cost function (9) for all admissible w(t) with the constraint condition and all admissible uncertainties, if there exist positive constants c₂, β, μ₁, μ₂, μ₃, and μ₄, symmetric positive- definite matrices X, Q, and Z, and real matrix Y, such that the following LMIs hold:

(33)

(34)

(35)

(36)

(37)

where

Proof. In order to deal with the uncertainties in inequality (12), we can rewrite it as the following inequality:

(38)

where

Thus, the aforementioned inequality (38) is equivalent to

(39)

where

(40)

Moreover, noticing the uncertainties which were described as the form in (2) and (6), we have

(41)

where

(42)

Using Lemma 8, it follows from (41) that

(43)

Thus, inequality (39) can be guaranteed by

(44)

Rewriting inequality (44) and applying Schur complement, we have

(45)

where

On the other hand, considering the uncertainties in inequality (34), we have

(46)

where

And can be expressed as

(47)

where

, L₃ = [S₁ 0],

, L₄ = [N 0].

Using Lemma 8, we know the following inequality holds by real positive scalars μ₃ and μ₄:

(48)

Hence, inequality (46) holds by the following inequality:

(49)

Rewriting (49) and using Schur complement, we have

(50)

where Λ₁₂ = C^T + K^TD^T.

Define X = P⁻¹, Y = KX, Z = XQX, pre- and postmultiplying inequality (45) by block-diagonal matrix diag {P⁻¹ I I I I I I}, and pre- and postmultiplying inequality (50) by a block-diagonal matrix diag {P⁻¹ I I I}. They lead to LMIs (33) and (34).

Finally, denote , , and set , and consider .

Then, inequality (13) can be guaranteed by

(51)

Using the Schur complement and eigenvalue transformation, we can get LMIs (35)–(37) from inequality (51). This completes the proof.

Remark 13. Notice that ; if α and T have been given, the value of system L₂-L_∞ performance γ only depends on β. Hence, we can obtain an optimal nonfragile robust finite-time L₂-L_∞ controller, and the scalar β can reduce to the minimum possible value such that LMIs (33)–(37) are satisfied. The optimization problem can be described as follows:

(52)

Remark 14. When the controller gain variations of the Lipschitz nonlinear systems (1) are of the multiplicative form [6, 18]:

(53)

with H and N being known constant matrices, and ρ(t) is the uncertain parameter matrix. In this case, the sufficient conditions for the nonfragile robust finite-time L₂-L_∞ control of the nonlinear systems (1) are identical to LMIs (33)–(37), except that XN^T, NX are changed to Y^TN^T, NY in inequalities (33) and (34), respectively. The proof of this conclusion is similar to Theorem 12.

Remark 15. By using the MATLAB LMIs Toolbox, the feasibility of Theorem 12 and Remark 3 can be easily checked. In Section 4, a simulation example about the Lipschitz nonlinear systems with state delays will be given.

4. Simulation Example

Consider system (1) with the following parameters:

(54)

In addition, we set c₁ = 0.5, δ = 1, T = 4, ε = 1.2, α = 0.5, d = 0.2, and

. The nonlinear function part in system (1) is chosen as the following form:

(55)

Then, for any

and

, we have

(56)

According to (16), we select the weighting matrices as follows

(57)

Remark 16. It is necessary to point out that the selection of the above weighting matrices not only needs to satisfy Assumption 2 but also needs to ensure that the LMI (33) is feasible. Namely, the LMIs designed in this note actually put a constraint on the size of the above weighting matrices.

By resorting to MATLAB LMIs Toolbox, solving Theorem 12 and Remark 13, respectively, we can obtain the following solutions under the above two cases.

Case 1. Let H = [0.3], N = [0.3 0.2], ρ(t) = (0.5/(1 + t²))I, Γ(t) = 0.8sin(t)I. Solving Theorem 12, which considering the additive controller gain variation, we get

(58)

with scalars value β = 45.4950, γ = 12.9647, and c₂ = 86.0363.

Case 2. Let H = [0.3], N = [0.5], ρ(t) = (0.5/(1 + t²))I, and Γ(t) = 0.8sin(t)I. Solving Remark 13, which is considering the multiplicative controller gain variation, we get

(59)

with scalars value β = 45.5722, γ = 12.9757, and c₂ = 86.1562.

In this note, with the initial states x₀ = [0.5 0.2]^T and the disturbance input is chosen as

(60)

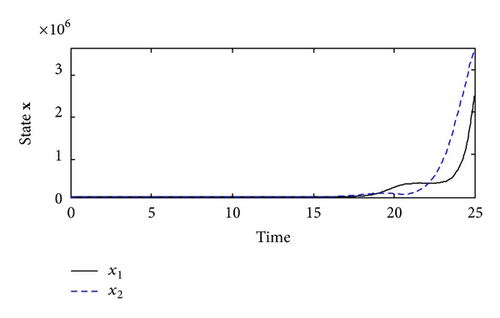
The trajectories of uncontrolled system state x(t) are depicted as Figure 1. The states and output simulation curves of closed-loop controlled system are, respectively, shown in Figures 2, 3, and 4 with the simulation time t ∈ [0 25]. Figure 5 shows the evolution of x^T(t)Rx(t) (t ∈ [0 4]) of the controlled system (7).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The trajectories of uncontrolled system state x(t).

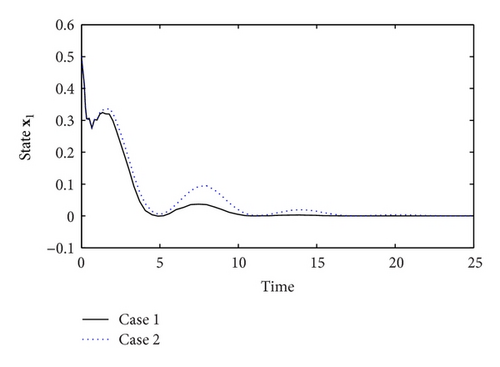
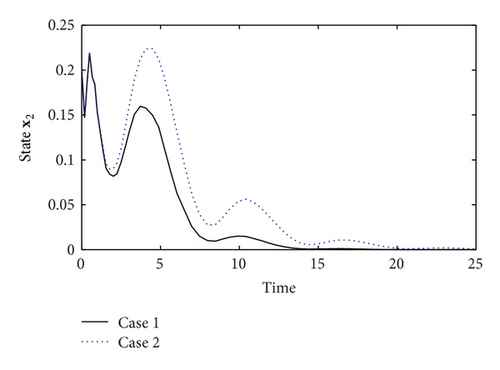
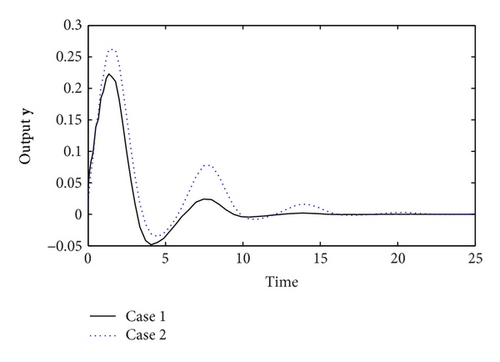
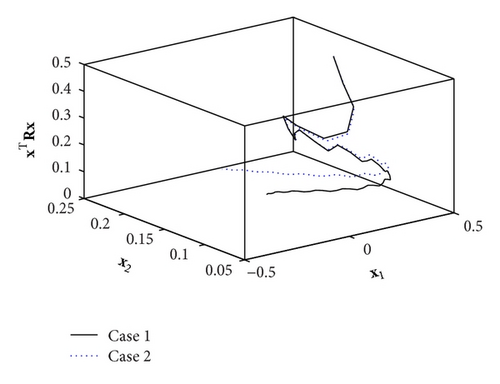
By calculation, we have (Case 1) and (Case 2). According to the above computing results and the simulation results, one can know that the nonfragile state feedback controller which was designed in this note can effectively guarantee that the concerned system (1) not only is finite-time bounded in fixed finite-time interval t ∈ [0 4] but also with an L₂-L_∞ disturbance performance level.

Remark 17. It should be pointed out that in the simulation example, according to Definition 4, as long as the choice of c₁ with the initial states is satisfied to . Then, the nonfragile state feedback controlled system is FTB (i.e., the closed-loop system trajectories stay within a given bound) and satisfies the L₂-L_∞ constraint condition (9).

5. Conclusions

In this paper, we have studied the nonfragile robust finite-time L₂-L_∞ control problem for a class of uncertain Lipschitz nonlinear systems with time-delays. By using the Lyapunov function approach and linear matrix inequality techniques, a sufficient condition for the existence of nonfragile robust finite-time L₂-L_∞ controller has been derived. Based on this condition, an optimization algorithm is provided to find nonfragile optimal control. Finally, a simulation example is presented to illustrate the effectiveness and applicability of the proposed approach.

Acknowledgments

This work was supported in part by the National Natural Science Foundation of China (Grant no. 61203051), the Key Program of Natural Science Foundation of Education Department of Anhui Province (Grant no. KJ2012A014), and the Joint Specialized Research Fund for the Doctoral Program of Higher Education (Grant no. 20123401120010).

References

1 Su X., Shi P., and Wu L., A novel approach to filter design for T-S fuzzy discrete-time systems with time-varying delay, IEEE Transactions on Fuzzy Systems. (2012) 20, no. 6, 1114–1129.
10.1109/TFUZZ.2012.2196522
Web of Science® Google Scholar
2 Su X., Shi P., Wu L., and Song Y. D., A novel control design on discrete-time Takagi-Sugeno fuzzy systems with time-varying delays, IEEE Transactions on Fuzzy Systems. (2012) https://doi.org/10.1109/TFUZZ.2012.2226941.
10.1109/TFUZZ.2012.2226941
Google Scholar
3 Li F. and Zhang X., Delay-range-dependent robust H_∞ filtering for singular LPV systems with time variant delay, International Journal of Innovative Computing, Information and Control. (2013) 9, no. 1, 339–353.
Google Scholar
4 Yoo S. J. and Park J. B., Decentralized adaptive output-feedback control for a class of nonlinear large-scale systems with unknown time-varying delayed interactions, Information Sciences. (2012) 186, no. 1, 222–238, https://doi.org/10.1016/j.ins.2011.10.004, MR2860022.
10.1016/j.ins.2011.10.004
Web of Science® Google Scholar
5 Gao H. J. and Wang C. H., Delay-dependent robust H_∞ and L₂-L_∞ filtering for a class of uncertain nonlinear time-delay systems, IEEE Transactions on Automatic Control. (2003) 48, no. 9, 1661–1666, https://doi.org/10.1109/TAC.2003.817012, MR2000128.
10.1109/TAC.2003.817012
Web of Science® Google Scholar
6 Xie N. and Tang G.-Y., Delay-dependent nonfragile guaranteed cost control for nonlinear time-delay systems, Nonlinear Analysis. Theory, Methods & Applications. (2006) 64, no. 9, 2084–2097, https://doi.org/10.1016/j.na.2005.08.005, MR2211201, ZBL1161.93315.
10.1016/j.na.2005.08.005
Web of Science® Google Scholar
7 Dorato P., Short time stability in linear time-varying systems, Proceedings of the IRE international Convention Record, 1961, New York, NY, USA, 83–87.
Google Scholar
8 Amato F., Ariola M., and Dorato P., Finite-time control of linear systems subject to parametric uncertainties and disturbances, Automatica. (2001) 37, no. 9, 1459–1463.
10.1016/S0005-1098(01)00087-5
Web of Science® Google Scholar
9 Weiss L. and Infante E. F., Finite time stability under perturbing forces and on product spaces, IEEE Transactions on Automatic Control. (1967) 12, 54–59, MR0209589, ZBL0168.33903.
10.1109/TAC.1967.1098483
Web of Science® Google Scholar
10 Moulay E., Dambrine M., Yeganefar N., and Perruquetti W., Finite-time stability and stabilization of time-delay systems, Systems & Control Letters. (2008) 57, no. 7, 561–566, https://doi.org/10.1016/j.sysconle.2007.12.002, MR2415969, ZBL1140.93447.
10.1016/j.sysconle.2007.12.002
Web of Science® Google Scholar
11 Amato F., Ambrosino R., Ariola M., and De Tommasi G., Robust finite-time stability of impulsive dynamical linear systems subject to norm-bounded uncertainties, International Journal of Robust and Nonlinear Control. (2011) 21, no. 10, 1080–1092, https://doi.org/10.1002/rnc.1620, MR2839840, ZBL1225.93087.
10.1002/rnc.1620
Web of Science® Google Scholar
12 Zhang W. H. and An X., Finite-time control of linear stochastic systems, International Journal of Innovative Computing, Information and Control. (2008) 4, no. 3, 687–694.
Google Scholar
13 Meng Q. and Shen Y., Finite-time H_∞ control for linear continuous system with norm-bounded disturbance, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 4, 1043–1049, https://doi.org/10.1016/j.cnsns.2008.03.010, MR2468938, ZBL1221.93066.
10.1016/j.cnsns.2008.03.010
Web of Science® Google Scholar
14 Liu L., Han Z., and Li W., Non-fragile observer-based passive control for uncertain time delay systems subjected to input nonlinearity, Nonlinear Analysis. Theory, Methods & Applications. (2010) 73, no. 8, 2603–2610, https://doi.org/10.1016/j.na.2010.06.039, MR2674095, ZBL1204.34101.
10.1016/j.na.2010.06.039
Web of Science® Google Scholar
15 Yang G.-H. and Che W.-W., Non-fragile H_∞ filter design for linear continuous-time systems, Automatica. (2008) 44, no. 11, 2849–2856, https://doi.org/10.1016/j.automatica.2008.03.018, MR2527206, ZBL1152.93365.
10.1016/j.automatica.2008.03.018
Web of Science® Google Scholar
16 Ren J. and Zhang Q., Non-fragile PD state H_∞ control for a class of uncertain descriptor systems, Applied Mathematics and Computation. (2012) 218, no. 17, 8806–8815, https://doi.org/10.1016/j.amc.2012.02.039, MR2921367, ZBL1245.93045.
10.1016/j.amc.2012.02.039
Web of Science® Google Scholar
17 Zhang J., Shi P., and Qiu J., Non-fragile guaranteed cost control for uncertain stochastic nonlinear time-delay systems, Journal of the Franklin Institute. (2009) 346, no. 7, 676–690, https://doi.org/10.1016/j.jfranklin.2009.04.001, MR2561579.
10.1016/j.jfranklin.2009.04.001
Web of Science® Google Scholar
18 Wo S., Zou Y., Chen Q., and Xu S., Non-fragile controller design for discrete descriptor systems, Journal of the Franklin Institute. (2009) 346, no. 9, 914–922, https://doi.org/10.1016/j.jfranklin.2009.07.008, MR2557591.
10.1016/j.jfranklin.2009.07.008
Web of Science® Google Scholar
19 Zhang J., Shi P., and Yang H., Non-fragile robust stabilization and H_∞ control for uncertain stochastic nonlinear time-delay systems, Chaos, Solitons and Fractals. (2009) 42, no. 5, 3187–3196, https://doi.org/10.1016/j.chaos.2009.04.049, MR2562824, ZBL1198.93189.
10.1016/j.chaos.2009.04.049
Web of Science® Google Scholar
20 Rotea M. A., The generalized H₂ control problem, Automatica. (1993) 29, no. 2, 373–385, https://doi.org/10.1016/0005-1098(93)90130-L, MR1211294, ZBL0772.93027.
10.1016/0005-1098(93)90130-L
Web of Science® Google Scholar
21 Chen A. and Wang J., Delay-dependent L₂-L_∞ control of linear systems with multiple time-varying state and input delays, Nonlinear Analysis. Real World Applications. (2012) 13, no. 1, 486–496, https://doi.org/10.1016/j.nonrwa.2011.08.006, MR2846858.
10.1016/j.nonrwa.2011.08.006
Web of Science® Google Scholar
22 Li L., Jia Y., Du J., and Yuan S., Robust L₂-L_∞ control for uncertain singular systems with time-varying delay, Progress in Natural Science. (2008) 18, no. 8, 1015–1021, https://doi.org/10.1016/j.pnsc.2008.03.005, MR2458775.
10.1016/j.pnsc.2008.03.005
Web of Science® Google Scholar
23 Wu L. and Wang Z., Robust L₂-L_∞ control of uncertain differential linear repetitive processes, Systems & Control Letters. (2008) 57, no. 5, 425–435, https://doi.org/10.1016/j.sysconle.2007.10.005, MR2405111.
10.1016/j.sysconle.2007.10.005
Web of Science® Google Scholar
24 He S. and Liu F., Robust L₂-L_∞ filtering of time-delay jump systems with respect to the finite-time interval, Mathematical Problems in Engineering. (2011) 2011, 17, 839648, https://doi.org/10.1155/2011/839648, MR2733600.
10.1155/2011/839648
Web of Science® Google Scholar
25 Abbaszadeh M. and Marquez H. J., Dynamical robust H_∞ filtering for nonlinear uncertain systems: an LMI approach, Journal of the Franklin Institute. (2010) 347, no. 7, 1227–1241, https://doi.org/10.1016/j.jfranklin.2010.05.016, MR2669300, ZBL1202.93157.
10.1016/j.jfranklin.2010.05.016
Web of Science® Google Scholar
26 Thuan M. V., Phat V. N., and Trinh H. M., Dynamic output feedback guaranteed cost control for linear systems with interval time-varying delays in states and outputs, Applied Mathematics and Computation. (2012) 218, no. 21, 10697–10707, https://doi.org/10.1016/j.amc.2012.04.039, MR2927085, ZBL1248.93073.
10.1016/j.amc.2012.04.039
Web of Science® Google Scholar
27 Liu Q., Wang R., and Wu D., Stability analysis for sampled-data systems based on multiple Lyapunov functional method, International Journal of Innovative Computing, Information and Control. (2012) 8, no. 9, 6345–6355.
Web of Science® Google Scholar
28 Rehan M., Hong K.-S., and Ge S. S., Stabilization and tracking control for a class of nonlinear systems, Nonlinear Analysis. Real World Applications. (2011) 12, no. 3, 1786–1796, https://doi.org/10.1016/j.nonrwa.2010.11.011, MR2781896, ZBL1217.93145.
10.1016/j.nonrwa.2010.11.011
Web of Science® Google Scholar

Citing Literature

All articles

Nonfragile Robust Finite-Time L₂-L_∞ Controller Design for a Class of Uncertain Lipschitz Nonlinear Systems with Time-Delays

Abstract

1. Introduction

2. Preliminaries and Problem Statement

3. Main Results

4. Simulation Example

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Nonfragile Robust Finite-Time L2-L∞ Controller Design for a Class of Uncertain Lipschitz Nonlinear Systems with Time-Delays

Abstract

1. Introduction

2. Preliminaries and Problem Statement

3. Main Results

4. Simulation Example

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information

Nonfragile Robust Finite-Time L₂-L_∞ Controller Design for a Class of Uncertain Lipschitz Nonlinear Systems with Time-Delays