Abstract and Applied Analysis
Volume 2013, Issue 1 262010
Research Article
Open Access

A Class of Spectral Element Methods and Its A Priori/A Posteriori Error Estimates for 2nd-Order Elliptic Eigenvalue Problems

Jiayu Han, 

Jiayu Han

School of Mathematics and Computer Science, Guizhou Normal University, Guiyang 550001, China gznu.edu.cn

Search for more papers by this author
Yidu Yang, 

Corresponding Author

Yidu Yang

School of Mathematics and Computer Science, Guizhou Normal University, Guiyang 550001, China gznu.edu.cn

Search for more papers by this author
First published: 27 October 2013
https://doi.org/10.1155/2013/262010
Citations: 6
Academic Editor: Rasajit Bera

Abstract

This paper discusses spectral and spectral element methods with Legendre-Gauss-Lobatto nodal basis for general 2nd-order elliptic eigenvalue problems. The special work of this paper is as follows. (1) We prove a priori and a posteriori error estimates for spectral and spectral element methods. (2) We compare between spectral methods, spectral element methods, finite element methods and their derived p-version, h-version, and hp-version methods from accuracy, degree of freedom, and stability and verify that spectral methods and spectral element methods are highly efficient computational methods.

1. Introduction

As we know, finite element methods are local numerical methods for partial differential equations and particularly well suitable for problems in complex geometries, whereas spectral methods can provide a superior accuracy, at the expense of domain flexibility. Spectral element methods combine the advantages of the above methods (see [1]). So far, spectral and spectral element methods are widely applied to boundary value problems (see [1, 2]), as well as applied to symmetric eigenvalue problems (see [3]). However, it is still a new subject to apply them to nonsymmetric elliptic eigenvalue problems.

A posteriorii error estimates and highly efficient computational methods for finite elements of eigenvalue problems are the subjects focused on by the academia these years; see [3–16], and among them, for nonsymmetric 2nd-order elliptic eigenvalue problems, [5, 15] provide a posteriori error estimates and adaptive algorithms, [9] the function value recovery techniques and [8, 10] two-level discretization schemes.

Based on the work mentioned above, this paper shall further apply spectral and spectral element methods to nonsymmetric elliptic eigenvalue problems. This paper will mainly perform the following work.
  • (1)

    We prove a priori and a posteriori error estimates of spectral and spectral element methods with Legendre-Gauss-Lobatto nodal basis, respectively, for the general 2nd-order elliptic eigenvalue problems.

  • (2)

    We compare between spectral methods, spectral element methods with Legendre-Gauss-Lobatto nodal basis, finite element methods, and their derived p-version, h-version, and hp-version methods from accuracy, degree of freedom, and stability and verify that spectral methods and spectral element methods are highly efficient computational methods for nonsymmetric 2nd-order elliptic eigenvalue problems.

This paper is organized as follows. Section 2 introduces basic knowledge of second elliptic eigenvalue problems. Sections 3 and 4 are devoted to a priori and a posteriori error estimates of spectral and spectral element methods, respectively. In Section 5, some numerical experiments are performed by the methods mentioned above.

2. Preliminaries

Consider the 2nd-order elliptic boundary value problem
()
where Ω ⊂ Rd (d = 2,3) is a bounded domain, b and c are a real-valued vector function and a real-valued function, respectively, and D is a positive scalar function with D(x) ≥ D0 > 0 (∀x ∈ Ω).

We denote the complex Sobolev spaces with norm ∥·∥m by Hm(Ω), . Let (·, ·) and ∥·∥0,Ω be a inner product and a norm in the complex space L2(Ω), respectively.

In this paper, C denotes a generic positive constant independent of the polynomial degrees and mesh scales, which may not be the same at different occurrences.

Define the bilinear form a(·, ·) as follows:
()
We assume that f ∈ L2(Ω), D,  b, and c are bounded functions on Ω, namely D, c ∈ L∞(Ω), b ∈ (L∞(Ω)) d. Further more, we assume that ∇·b exists and satisfies
()
Under these assumptions, the bilinear form a(·, ·) is continuous in and -elliptic; that is, there exist two constants A, B > 0 independent of w, v such that
()
The corresponding variational formulation of (1) is given as follows: find , such that
()
The adjoint problem of (5) is as follows: find , such that
()
As the general 2nd-order elliptic boundary value problems, we assume that the regularity estimates for problem (5) and its adjoint problem (6) hold, respectively. Namely
()
()

We assume that Kh = {κ} is a regular rectangle (resp. cuboid) or simplex partition of the domain Ω and satisfies . We associate with the partition a polynomial degree vector N = {Nκ}, where Nκ is the polynomial degree in κ. Let hκ be the diameter of the element κ, and let .

We define spectral and spectral element spaces as follows:
()
where PN(Ω) and are polynomial spaces of degree N (resp. degree N in every direction) in Ω and degree Nκ (resp. degree Nκ in every direction) in the element κ, respectively.
The spectral approximation of (5) is as follows: find wN ∈ SN(Ω), such that
()
The spectral element approximation of (5) is as follows: find wN,h ∈ SN,h(Ω), such that
()

We assume that f ∈ L2(Ω) and derive from Lax-Milgram theorem that the variational formations (5), (6), (10), and (11) have a unique solution, respectively.

Define the interpolation operators
()
as the interpolations in the element κ and the domain Ω, respectively, with the tensorial Legendre-Gauss-Lobatto (LGL) interpolation nodes.
Define the interpolation operator
()

We quote from [2] (see (5.8.27) therein) the interpolation estimates for spectral and spectral element methods with LGL Nodal-basis as follows.

For all ,
()
()
For all v ∈ Hs(Ω), s ≥ (d + 1)/2,
()
()
We assume that the solution of boundary value problem (5) , that wN and wN,h are the solutions of (10) and (11), respectively; then we derive from Céa lemma and the interpolation estimates that
()
()
where sκ ≥ (d + 1)/2, ∀κ ∈ Kh.
Particularly, if Nκ = N, ∀κ ∈ Kh, then we have
()

Note that (18) is also suited to spectral methods with modal basis (see [1, 2]).

Using Aubin-Nitsche technique, we deduce from the regularity estimate (8) and the estimates (18)–(20) the priori estimates of boundary value problem (5) for spectral and spectral element methods; that is,
()
()

3. Spectral and Spectral-Element Approximations and Error Estimates for Eigenvalue Problems

3.1. Spectral and Spectral-Element Approximations for Eigenvalue Problems

Consider the following eigenvalue problem corresponding to the boundary value problem (1):
()
The variational formation of (23) is given by the following: find , such that
()
The spectral approximation scheme of (24) is given by the following: find λN ∈ ℂ, 0 ≠ uN ∈ SN(Ω), such that
()
The spectral element approximation scheme of (24) is given by the following: find λN,h ∈ ℂ, 0 ≠ uN,h ∈ SN,h(Ω), such that
()
Define the solution operators , and TN,h : L2(Ω) → SN,h(Ω) by
()
Obviously (see [17]), the equivalent operator forms for (24) and (26) are the following.
Find , such that
()
Find λN,h ∈ ℂ, 0 ≠ uN,h ∈ SN,h(Ω), such that
()
The adjoint problem of the eigenvalue problem (23) is
()
where L*u* = −∇·(D∇u*) − b · ∇u* + (c − ∇·b)u*.
The variational formation of (30) is given by the following: find , such that
()
The spectral element approximation scheme of (31) is given by the following: find , such that
()
We can likewise define the equivalent operator forms for the eigenvalue problems (31) and (32) as
()

Let λ be an eigenvalue of (23). There exists a smallest integer μ, called the ascent of λ, such that ker ((λ−1 − T) μ) = ker ((λ−1 − T) μ+1). q = dim  ker ((λ−1 − T) μ) is called the algebraic multiplicity of λ. The functions in ker ((λ−1 − T) μ) are called generalized eigenfunctions of T corresponding to λ. Likewise the ascent, algebraic multiplicity and generalized eigenfunctions of λN,h, λ* and can be defined.

Let λ be an eigenvalue of (23) with the algebraic multiplicity q and the ascent μ. Assume ; then there are eigenvalues λj,N,h (j = 1,2, …, q) of (26) which converge to λ. Let M(λ) be the space spanned by all generalized eigenfunctions corresponding to λ of T, and let MN,h(λ) be the space spanned by all generalized eigenfunctions corresponding to all eigenvalues of TN,h that converge to λ.

In view of adjoint problems (31) and (32), the definitions of M*(λ*) and are analogous to M(λ) and MN,h(λ). Let , and let .

Note that when b = 0, both (24) and (26) are symmetric. Thus, the ascent μ = 1 of λ, and the ascent l = 1 of λN,h.

3.2. A Priori Error Estimates

We will analyze a prior error estimates for spectral element methods which are suitable for spectral methods with mesh fineness h not considered.

Assume that R and U are two closed subspace in .

Denote
()
We say that θ(R, U) is the gap between R and U.
Denote
()

We give the following four lemmas from Theorem 8.1–8.4 in [17], which are applications to spectral element methods.

Lemma 1. Assume . For small enough h and big enough N, there holds

()

Lemma 2. Assume ; then

()

Lemma 3. Assume that ; then there holds

()
Since ker ((λ−1 − T) l) (l ≥ 1) is a finite dimensional space, there exists a direct-sum decomposition . We define the operator El as a projection along Ml from to ker ((λ−1 − T) l).

Lemma 4. Assume . Let λN,h be an eigenvalue of TN,h and lim N→∞,h→0λN,h = λ. uN,h satisfies and , where k ≤ μ is a positive integer. Then, for every integer l ∈ [k, μ], there holds

()

We assume that in this section, for the sake of simplicity, Nκ = N, ∀κ ∈ Kh.

Theorem 5. If and , then there holds the following error estimates:

()
()
()
Let , and let , for some l1 ≤ μ. Then, for every integer l2(l1 ≤ l2 ≤ μ), there exists a function u′, such that and
()
where τ1 = min (N + 1, t1), τ2 = min (N + 1, t2).

Proof. We derive from the error estimate (20) that

()
By (14),
()
Analogically,
()
Plugging the two inequalities above into (36), (38), and (39) yields (42), (41), and (43), respectively. We find from (37) that
()
combining with (45) and (46) yields (40).

Supposing that , ρ(T) is a regular set of T, and Γ ⊂ ρ(T) is a closed Jordan curve enclosing λ−1.

Denote
()
Define the spectral projection operators
()

We give the following lemma by referring to [18, 19] (see proposition 5.3 in [18] and theorem 1.3.2 in [19]).

Lemma 6. If , then there holds that EN,h → E(p), R(TN,h, z) is uniformly bounded with N and h, and

()

Theorem 7. Under the assumptions of Theorem 5, further assume that the ascent of λ is μ = 1. Let (λN,h, uN,h) be an eigenpair of (26) with ; then there exists an eigenpair (λ, u) of (24), such that

()
()
()
where τ1 = min (N + 1, t1) and τ2 = min (N + 1, t2).

Let (λ, u) be an eigenpair of (24). If λN,h is an eigenvalue of (26) convergence to λ, then there exists , such that (51)–(53) hold.

Proof. We deduce (53) immediately from (41). We derive from (22) and (7) that

()
thus,. Taking u = EuN,h and by virtue of , Lemma 6 and (22), we have
()
from which follows
()
which is (52). By direct calculation, we have
()
Plugging (20), (52), and (53) into (57) yields (51).

If (λ, u) is an eigenpair of (24), let uN,h = EN,hu; by the same argument we can prove (51) and (52).

4. A Posteriori Error Estimates

Based on [20], we will discuss a posteriori error estimates. We further assume that Ω ⊂ R2, the partition Kh is γ-shape regular, and the polynomial degree of neighboring elements are comparable; that is, there exists γ > 0, such that for all κ, κ′ ∈ Kh, ,
()

We refer to the hp-clément interpolation estimates given by [20, 21] (see theorems 2.2 and 2.3, respectively), which generalize the well-known clément type interpolation operators studied in [22] and [23] to the hp context.

Lemma 8. Assume that the partition Kh is γ-shape regular and the polynomial distribution N is comparable. Then there exists a positive constant C = C(γ) and the clément operator , such that

()
()
where he is the length of the edge e and , where κ1, κ2 are elements sharing the edge e and ωκ, ωe are patches covering κ and e with a few layers, respectively.

Define interval and weight function . Denote the reference square and triangle element by and , respectively. Define weight function .

The following three lemmas are given by [20]. Lemmas 9–10 provide the polynomial inverse estimates in standard interval and element, while Lemma 11 provides a result for the extension from an edge to the element.

Lemma 9. Let −1 < α < β, σ ∈ [0,1]. Then there exists C = C(α, β), such that for all N ∈ ℕ and all univariate polynomials πN of degree N,

()

Lemma 10. Let −1 < α < β, σ ∈ [0,1]. Then there exist C1 = C(α, β), C2 = Cσ > 0, such that for all N ∈ ℕ and all polynomials πN of degree bi-N,

()
()

Lemma 11. Let , ; then there exists Cα > 0 such that for all N ∈ ℕ, ε ∈ (0,1], and all univariate polynomials π of degree N, there exists an extension and holds

()
()
()

It is easy to know that the three lemmas above hold for complex-valued polynomials.

Let Dκ, bκ, and cκ be the interpolations of D, b, and c in κ with the polynomial degree Nκ (resp. degree Nκ in every direction), respectively, or the L2(κ)-projection on the space of polynomials with degree Nκ. For convenient argument, here and hereafter we assume that (λ, u) and are the eigenpairs of the eigenvalue problem (24) and its adjoint problem (31), respectively. (λN,h, uN,h) and are the solutions of the corresponding spectral element approximations (26) and (32), respectively.

Denote
()
Define the local error indicators
()
Their first terms are the weighted element internal residuals given by
()
Their second terms are the weighted element boundary residuals given by
()
where we denote the jump of the normal derivatives of uN,h and across the edges by [∂uN,h/∂n] and , respectively. he is the length of edge e. The weight functions Φκ and Φe are scaled transformations of the weight functions and ; that is, if Fκ is the element map for element κ and e is the image of the edge under Fκ, then
()
where we choose Cκ, Ce > 0, such that
()
We define the global error indicators as follows:
()

Theorem 12. Let α ∈ [0,1]. Then there exists a constant C > 0 independent of h, N, and κ, such that

()

Proof. We denote w : = u − uN,h − I(u − uN,h), where I is hp-clément operator given by Lemma 8. We derive from -elliptic of a(·, ·) that

()
Therefore,
()
which together with
()
and using Cauchy-Schwartz inequality, the hp-clément interpolation estimates in Lemma 8 then yield
()

Using scaled transformation and setting α = 0, β = α in (61) and (62), we get and ; then this proof concludes.

For the adjoint eigenvalue problem, we still have the following.

Theorem 13. Let α ∈ [0,1]. Then there exists a constant C > 0 independent of h, N, and κ, such that

()

Lemma 14. Let α ∈ [0,1], ε > 0. Then there exists a constant C(ε) > 0 independent of h, N, and κ, such that

()

Proof. We denote with α ∈ (0,1] and extend vκ to Ω by vκ = 0 on Ω∖κ; then

()
We consider the H1 semi norm for vκ. Using the polynomial inverse estimates (62)-(63) in Lemma 10, by transformation between the reference element and κ, we find for α > 1/2 that
()
Note that (62) is applicable since α > 1/2 implies 2(α − 1)>−1; thus, we set β = α, α = 2(α − 1) in (62); then the third inequality above holds.

Since , we obtain

()
To obtain an upper bound in the case of 0 ≤ α ≤ 1/2, we use the polynomial inverse estimate (62) in Lemma 10; for β > 1/2, we derive from (62) that
()
Setting β = 1/2 + ε, ε > 0,
()
We obtain the desired result immediately from (83) and (85).

In order to obtain a local upper bound for the error indicator ηα;κ, we consider the edge residual term . we introduce the set
()

Lemma 15. Let α ∈ [0,1], ε > 0. Then there exists a constant C(ε) > 0 independent of h, N, and κ, such that

()

Proof. We will use weight functions on edge and a suitable extension operator. For a given element κ with edge e, we choose the element κ1 so that ∂κ1∩∂κ = e. Denote ; we construct a function with as follows.

Let (Ce is defined by (71)). Using Lemma 11, we extend to , where the polynomial π corresponds to CeDκ[∂uN,h/∂n]. Define we|κ and as the affine transformation of in ; Thus, we is a piecewise H1-function. From (64), we know we vanishes on ∂κe; Therefore, . It is trivial to extend we to Ω, such that we = 0 in Ω∖κe. We find

()
Therefore,
()
We consider the case of α ∈ (1/2,1] first. Using the affine equivalence and (65)-(66) in Lemma 11, we obtain the upper bounds for and as follows:
()
It follows from (89)-(90) that
()
By the definition of and setting α = 0 in Lemma 14, we get
()
by the triangle inequality
()
Combining the three inequalities above and summing, we have
()

Setting in the above inequality yields the assertion for α > 1/2. For the case of α ∈ [0,1/2], we set β = 1/2 + ε, use (62) in Lemma 10 to get , and find the desired result.

Combining Lemmas 14 and 15, we obtain the following theorem.

Theorem 16. Let α ∈ [0,1], ε > 0. Then there exists a constant C > 0 independent of h, N, and κ, such that

()

Similarly, we have Theorem 17.

Theorem 17. Let α ∈ [0,1], ε > 0. Then there exists a constant C > 0 independent of h, N, and κ, such that

()

In order to estimate bounds of |λ − λN,h|, we also need Lemma 18 (see [8, 10]).

Lemma 18. Let (λ, u) be an eigenpair of (24), and let be the associated eigenpair of the adjoint problem (31). Then for all , (w, w*) ≠ 0,

()

Theorem 19. Under the assumptions of Theorem 7, we assume that D, b, and c are smooth enough, and let α ∈ [0,1]. Then there exists an eigenpair (λ, u) of (24), such that

()
()
Further let the ascent of λN,h be l = 1, and let be the corresponding adjoint eigenpair of (32), then there exists an adjoint eigenpair (λ*, u*) of (31), such that
()
Particularly, if the eigenvalue problem (23) is symmetric (i.e., b = 0), then
()

Proof. We know from the assumption . By the interpolation error estimates (14) and (15), we have

()
From , we know that . By the interpolation error estimate on edge of element (see formula (5.4.42) in [2]), we get
()
Note that the formula (51) gives the optimal orders of convergence; thus, we deduce that the second and third terms on the right side of (74) are higher order infinitesimals. We derive from (52) and (53), and N = Nκ, that
()
Therefore, the fourth term on the right side of (74) is also a higher order infinitesimal. Up to higher order terms, we get (98). We ignore higher order infinitesimals in (95) and get (99). From Lemma 4 in [10], we know that and is uniformly bounded with h and N. By the same argument of (98), we can deduce that
()
From (97), we have
()
that is,
()
Substituting (98) and (105) into the above equality, we obtain (100).

If the eigenvalue problem (23) is symmetric (i.e., b = 0), then

()
Up to higher order term λ(uN,h − u, uN,h − u), by (99) we get (101).

Remark 20. Babuška and Osborn [17] have discussed hp finite element approximation with simplex partition for eigenvalue problems. Obviously, the Interpolation estimates (14) and (15) hold for hp finite element with simplex partition (see [24]). Therefore, our theoretical results of spectral methods and spectral methods for eigenvalue problems, which have been discussed in Sections 3 and 4, hold for hp finite element with simplex partition.

5. Numerical Experiments

In this section, we simply denote spectral methods, spectral element methods, and finite element methods with SM, SEM, and FEM, respectively. And spectral methods with equidistant nodal basis, modal basis, and LGL nodal basis are replaced by Eq-SM, Modal-SM, and LGL-SM, respectively. Note that all these methods employ the tensorial basis.

In our experiment, we compute as condition number for simple eigenvalue (see Remark 2.1 in [25]), where uN,h and are eigenfunctions of eigenvalue problem (25) and its adjoint problem (32) normalized with ∥·∥0,Ω, respectively.

5.1. Example 1

Consider the nonsymmetric eigenvalue problem
()

The first eigenvalue of (109) λ1 = 101/4 + 2π2 is a simple eigenvalue. And the corresponding eigenfunctions are sufficiently smooth.

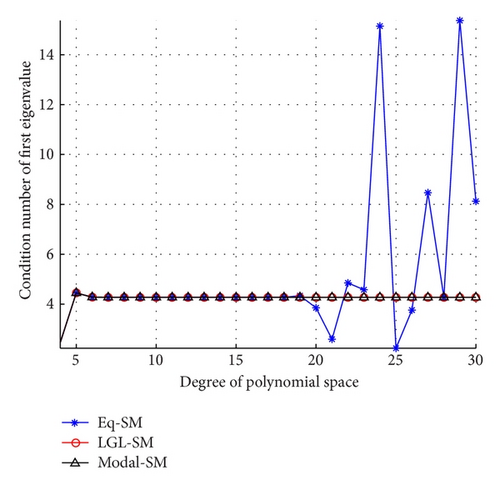
5.1.1. Comparisons between LGL-SM, Modal, and Eq-SM

Figure 1 shows that the condition numbers of the first eigenvalue for LGL-SM, Modal-SM, and Eq-SM coincide with each other at the beginning but perform abnormally with N > 19 for Eq-SM. Table 1 tells us that when N > 11, the accuracy of first eigenvalue obtained by Eq-SM is not as good as obtained that by LGL-SM and Modal-SM. When N = 15, the error of the first eigenvalues obtained by Eq-SM is greater than 1E-5; however, the order of the magnitude of errors for LGL-SM and Modal-SM still keeps below 1E-13. The best result of first eigenvalue error for Eq-SM is merely 1E-9 or so.

Table 1. Errors of LGL-SM, modal, and Eq-SM for 1st eigenvalue.
N DOF LGL-SM Modal-SM Eq-SM
λ1 λ1 λ1
4 9  5.19E + 00  5.19E + 00  5.19E + 00 
5 16  4.51E − 01  4.51E − 01  4.51E − 01 
6 25  7.68E − 03  7.68E − 03  7.68E − 03 
7 36  1.07E − 05  1.07E − 05  1.07E − 05 
8 49  1.21E − 05  1.21E − 05  1.21E − 05 
9 64  9.16E − 07  9.16E − 07  9.16E − 07 
10 81  2.46E − 08  2.46E − 08  2.48E − 08 
11 100  2.91E − 10  2.91E − 10  4.35E − 09 
12 121  9.31E − 13  1.06E − 12  2.79E − 08 
13 144  5.68E − 14  1.28E − 13  1.41E − 07 
14 169  2.84E − 14  1.28E − 13  2.28E − 06 
15 196  7.82E − 14  2.13E − 14  3.60E − 05 
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Condition number of first eigenvalue for SM.

5.1.2. LGL-SM and Modal-SM versus hp-SEM

Tables 1 and 2 indicate that increasing the polynomial degree N or decreasing the mesh fineness h can decrease the errors of the first eigenvalue. But it is expensive to increase polynomial degree and decrease mesh fineness h at the same time. For h = 1/4 and h = 1/16, we obtain from Table 2 the first eigenvalue errors 2.8E − 14 and 1.3E − 13 and the corresponding degree of freedom 1225 and 6241 for hp-SEM, respectively, Whereas from Table 1, to reach this accuracy, LGL-SM and Modal-SM should merely perform the interpolation approximations with polynomial degree bi-14 and bi-13 or so, and the corresponding degrees of freedom are merely 169 and 144, respectively. Therefore, we conclude that LGL-SM and Modal-SM are highly accurate and efficient for this kind of nonsymmetric eigenvalue problems.

Table 2. Errors and DOF of hp-SEM for the first eigenvalue.
N h = 1/2 h = 1/4 h = 1/8 h = 1/16
Error DOF Error DOF Error DOF Error DOF
2  5.18E + 00 9  2.54E − 01 49  1.50E − 02 225  9.00E − 04 961
3  7.00E − 03 25  6.10E − 04 121  1.20E − 05 529  1.90E − 07 2209
4  8.40E − 03 49  2.60E − 05 225  9.70E − 08 961  3.70E − 10 3969
5  1.64E − 04 81  1.60E − 07 361  1.50E − 10 1521  1.30E − 13 6241
6  4.10E − 07 121  2.30E − 11 529  9.90E − 13 2209  3.60E − 12 9025
7  3.10E − 08 169  1.70E − 12 729  3.10E − 13 3025  1.60E − 12 12321
8  1.90E − 10 225  1.90E − 13 961  2.10E − 12 3969  4.80E − 12 16129
9  5.50E − 13 289  2.80E − 14 1225  6.00E − 13 5041  1.10E − 12 20449
10 3.80E − 13 361  1.10E − 12 1521  4.40E − 12 6241  1.50E − 11 25281

In Figure 2 from [9], when the degree of freedom is up to 1000, the error of linear FEM is about 1E-2; the function value recovery techniques in [9] obviously improves the accuracy up to 1E-5. Comparing Tables 1 and 2 in this paper with Figure 2 in [9], we can also find the advantages of LGL-SM, Modal-SM, and hp-SEM over the function value recovery techniques for FEM given by [9] from accuracy and degree of freedom.

5.1.3. hp-SEM versus hp-FEM

From Table 4, we find that the condition number of the first eigenvalue for hp-version methods (hp-SEM and hp-FEM) stays at 4.27. It is indicated from Tables 2 and 3 that, when N is greater than 7, compared with hp-SEM, the errors of hp-FEM tend to become large, whereas the errors of hp-SEM still keep stable or even stay a decreasing tendency; however, this phenomenon is not apparent for h = 1/2.

Table 3. Errors of hp-FEM for the first eigenvalue.
N h = 1/2 h = 1/4 h = 1/8 h = 1/16
3  7.00E − 03  6.10E − 04  1.20E − 05  1.90E − 07
4  8.40E − 03  2.60E − 05  9.70E − 08  3.70E − 10
5  1.60E − 04  1.60E − 07  1.50E − 10  1.30E − 12
6  4.10E − 07  2.40E − 11  3.60E − 13  8.60E − 12
7  3.10E − 08  6.10E − 12  1.30E − 11  3.00E − 11
8  1.80E − 10  3.10E − 11  2.30E − 10  2.10E − 10
9  7.50E − 11  3.40E − 11  6.80E − 10  7.40E − 10
10  2.50E − 11  9.90E − 10  8.70E − 09  6.60E − 09
11  2.00E − 09  9.60E − 09  8.90E − 09  5.40E − 07
Table 4. Condition number of first eigenvalue for hp-SEM.
N h = 1/2 h = 1/4 h = 1/8 h = 1/16
3 4.284381324 4.270132842 4.269625046 4.269615821
4 4.267343095 4.269607452 4.269615638 4.26961567
5 4.269636446 4.269615725 4.26961567 4.26961567
6 4.269619135 4.26961567 4.26961567 4.26961567
7 4.269615617 4.26961567 4.26961567 4.26961567
8 4.26961567 4.26961567 4.26961567 4.26961567
9 4.26961567 4.26961567 4.26961567 4.26961567

Remark 21. Condition numbers of 1st eigenvalue for hp-FEM (not listed in Table 4) are almost the same to those for hp-SEM.

5.1.4. Validity of the Error Indicator

Denote
()

From Theorem 19, we know that ψα is a reliable error indicator for λN,h. We choose ψ0 (setting α = 0 in (110)) as a posteriorii error indicator.

In Figures 2 and 3, we denote the true error and est. error with |λN,h − λ| and ψ0, respectively.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The Error indicator ψ0 of LGL-SM.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The Error indicator ψ0 of hp-SEM (h = 1/2).

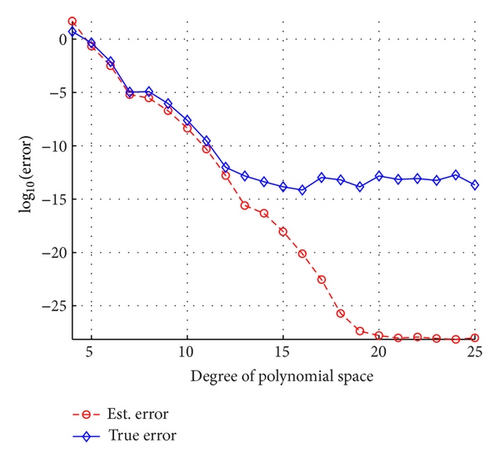
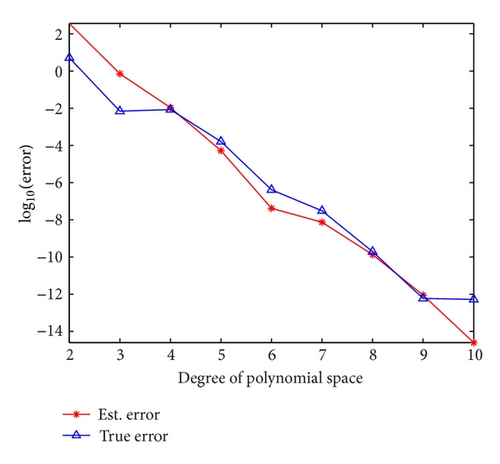
As is depicted in Figure 2, when the polynomial degree N ≤ 12, the error indicator ψ0 can properly estimate the true errors of LGL-SM for the first eigenvalue, however, also slightly underestimate the true errors. It is easy to see that ψ0 shows almost the same algebraic decay as the true error with the polynomial degree N (≤12) increasing. Nevertheless, the error indicator ψ0 cannot approximate the true errors if N is large enough, which is caused by round-off errors derived from the bad condition number of eigenvalue. In Figure 3, we give the comparison between the error indicator ψ0 and the true errors for hp-SEM.

5.2. Example 2

Consider the nonsymmetric eigenvalue problem
()

A reference value for the first eigenvalue (simple eigenvalue) of (111) is 34.6397 given by [5]. And the corresponding eigenfunctions have the singularity at the origin. Next, we shall compare the relevant numerical results between P-SEM and the other methods adopted in this paper. Note that here and hereafter P-version methods are for the fixed mesh fineness h = 1. Table 5 lists part data of the approximate eigenvalues computed by P-SEM and the corresponding error indicator ψ0 for reference.

Table 5. The Approximate eigenvalues and indicator ψ0 of P-SEM.
N   λN,h ψ0
3 28.56900 2.72E + 01 
4 31.99175 3.49E + 00 
5 34.82082 2.25E − 01 
6 34.65087 1.31E − 02 
7 34.65057 3.32E − 03 
8 34.64765 1.92E − 03 
9 34.64567 1.22E − 03 
10 34.64432 8.11E − 04 
11 34.64335 5.62E − 04
12 34.64265 4.02E − 04
13 34.64212 2.95E − 04
14 34.64171 2.22E − 04
15 34.64139 1.71E − 04
16 34.64114 1.33E − 04
17 34.64094 1.06E − 04
18 34.64078 8.49E − 05

5.2.1. Stability of P-Version Methods

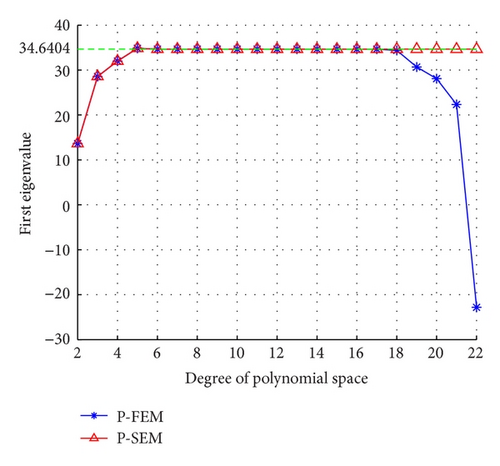
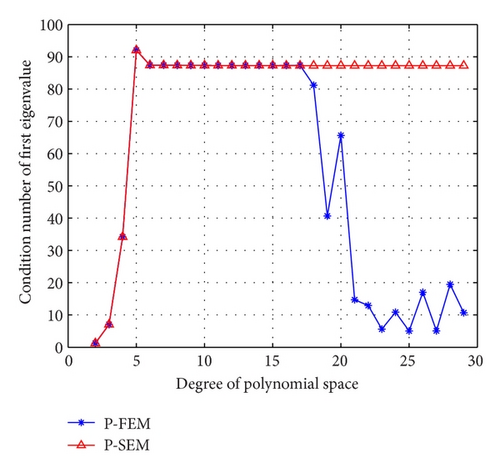
Figure 4 indicates that the eigenvalues computed by P-FEM will not seriously deviate from the results computed by P-SEM until the interpolation polynomial degree N is up to 19. This phenomenon coincides with the abnormity of condition number of first eigenvalue for P-FEM (see Figure 5). The reason is that the singularities of the eigenfunctions limit the accuracy of both kinds of methods; this is slightly different from the case of the eigenvalue problem with the sufficiently smooth eigenfunctions.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The Approximate 1st eigenvalue of P-SEM and P-FEM.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Condition number of first eigenvalue for P-SEM and P-FEM.

5.2.2. P-SEM versus Other Methods

By calculations, we find that, in the case of the linear FEM, for fixed mesh fineness h = 1/256, the approximate eigenvalue is 34.6403 with degree of freedom up to 195585. But P-SEM with the polynomial degree bi-22 can reach this accuracy, and the corresponding degree of freedom is merely 1365. Compared with the linear FEM, hp-SEM can obtain a higher accuracy with less degrees of freedom as follows: for fixed h = 1/16 and N = 10, the approximate eigenvalue is 34.63984 with degree of freedom 76161 but P-SEM with polynomial degree bi-44 can reach this accuracy. Therefore, P-SEM is more efficient for the eigenvalue problems with the singular solutions than the other methods.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant no. 11161012) and the Educational Administration and Innovation Foundation of Graduate Students of Guizhou Normal University (no. 2012(11)).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.