Abstract and Applied Analysis
Volume 2013, Issue 1 246724
Research Article
Open Access

Removing the Correlation Term in Option Pricing Heston Model: Numerical Analysis and Computing

R. Company, 

R. Company

Instituto Universitario de Matemática Multidisciplinar, Universitat Politècnica de València, Camino de Vera s/n, 46022 Valencia, Spain upv.es

Search for more papers by this author
L. Jódar, 

Corresponding Author

L. Jódar

Instituto Universitario de Matemática Multidisciplinar, Universitat Politècnica de València, Camino de Vera s/n, 46022 Valencia, Spain upv.es

Search for more papers by this author
M. Fakharany, 

M. Fakharany

Instituto Universitario de Matemática Multidisciplinar, Universitat Politècnica de València, Camino de Vera s/n, 46022 Valencia, Spain upv.es

Search for more papers by this author
M.-C. Casabán, 

M.-C. Casabán

Instituto Universitario de Matemática Multidisciplinar, Universitat Politècnica de València, Camino de Vera s/n, 46022 Valencia, Spain upv.es

Search for more papers by this author
First published: 12 June 2013
https://doi.org/10.1155/2013/246724
Citations: 6
Academic Editor: T. Diagana

Abstract

This paper deals with the numerical solution of option pricing stochastic volatility model described by a time-dependent, two-dimensional convection-diffusion reaction equation. Firstly, the mixed spatial derivative of the partial differential equation (PDE) is removed by means of the classical technique for reduction of second-order linear partial differential equations to canonical form. An explicit difference scheme with positive coefficients and only five-point computational stencil is constructed. The boundary conditions are adapted to the boundaries of the rhomboid transformed numerical domain. Consistency of the scheme with the PDE is shown and stepsize discretization conditions in order to guarantee stability are established. Illustrative numerical examples are included.

1. Introduction

It is well recognized that the Black-Scholes model, where the prices depend only on the variance of the stock returns, leads to unreliable prices associated with the hypothesis of lognormal distribution of the asset returns and constant volatility. Since 1993, [1] it is known that volatility is a function of both the strike and the expiry date of the derivative security. Empirical evidence suggests that asset price volatility is not constant by variable and stochastic [2].

There are two prominent ways of working around this problem, namely, local volatility models [1] and stochastic volatility models [2–4].

Stochastic volatility models have the following general pattern:
()
where the tradable security S(t) and its variance v(t) are correlated; that is, the Wiener stochastic processes satisfy dW1dW2 = ρdt, and the functional form of pS, qS, pv, and qv are determined by the model.

The model proposed by Heston, see [3], [5, chapter 10], takes into account nonlognormal distribution of the assets returns, leverage effect, and important mean-reverting property of volatility and has a closed formula when the parameters are constant [3] or piecewise constant [6].

According to (1), the model of Heston is specified as follows:
()
where W1, W2 are standard Brownian motions, μ represents the deterministic drift, κ is the mean reversion rate, θ is the long-run variance, σ is the volatility of the variance, and ρ is the correlation parameter.
Applying the Itô lemma and standard arbitrage arguments leads to the partial differential equation [3, page 329–335] for the price U = U(S, v, t) of a contingent claim:
()
()
A European vanilla call option with strike price E and maturity T satisfies (3) together with the payoff final condition
()
and the boundary conditions
()
()
()
()
where are related to κ, θ by means of the expression ;  , and λ is the market price of the volatility risk.

For constant parameters, Heston [3] uses the method of characteristic functions to derive a closed-form solution involving infinite integrals. When the parameters are piecewise constant in time, one can still derive a recursive closed formula using a PDE method [6] or a Markov argument in combination with affine models [7].

For the case where coefficients are time dependent, the authors in [8] use a small volatility of volatility expansion and Malliavin calculus techniques, to derive approximate analytical solutions. Reliable numerical methods for solving problems (3)–(9) are suitable for both situations, the general time-dependent coefficient case as well as for the constant parameter case, where the closed form proposed solutions require a further numerical treatment.

There are some approaches for the numerical treatment of stochastic volatility models such as sparse wavelet [9], spectral methods [10], and finite-difference methods [11–15].

A feature of the time dependent, two-dimensional convection-diffusion-reaction equation (3) is the presence of a mixed spatial derivative. Dealing with finite-difference methods, this fact involves the existence of negative coefficient terms into the numerical scheme and deteriorates the quality of the numerical solution; see the introduction of  [16].

Furthermore, finite difference schemes in the presence of a mixed spatial derivative produces four terms more in the numerical scheme with the corresponding additional computational cost and possible rounding accumulation error.

Both papers [13, 15] construct difference schemes involving the mixed spatial derivative with associated drawbacks. Reference [13] derives a compact finite difference scheme using a nine-point computational stencil. [15] propose three splitting schemes of the alternating direction implicit (ADI) type.

In this paper, we construct explicit finite difference schemes with positive coefficients for solving the Heston model (3)–(9) for the continuously time-dependent coefficient case of the mean reversion rate and long-run variance, after removing the mixed spatial derivative. The organization of the paper is as follows. The problems coming out from negative coefficients arising from the discretization of the diffusion term are not easily remedied [16]; thus, Section 2 addresses the removing of the mixed spatial derivative in (3) by means of the classical technique for the reduction of second-order linear partial differential equations in two variables to canonical form. We also determine the rhomboid nonrectangular numerical domain where the problem is discretized after the transformation. In Section 3, we construct an explicit difference scheme with only a five-points computational stencil. The boundary conditions are adapted to the boundaries of the numerical domain. Section 4 deals with the consistency of the scheme with (3). In Section 5, we study stepsize discretization conditions in order to guarantee the positivity and stability of the numerical scheme. In Section 6, illustrative numerical examples are included.

For a matrix A = (aij) m×n in ℝm×n, we denote by ∥A∥ = max {|aij | ; 1 ≤ i ≤ m, 1 ≤ j ≤ n} and by ∥A∥1 the maximum absolute column sum norm
()
see [17, page 56].

2. On the Transformation Problem and Its Motivation

Recently, the authors used space-centered forward in time explicit finite difference schemes for the computation and numerical analysis of several one-dimensional option pricing problems [18–20].

Following these ideas for the two-dimensional problem (3) one gets the following:
()
where τ = T − t,   k = Δτ,   h1 = ΔS,   h2 = Δv,   Si = ih1,   vj = jh2, and τn = nk.
By discretizing (3) one achieves the following scheme:
()

Note that if ρ ≠ 0, that is, when variables S and v are correlated, in the last term of the right-hand side of the scheme, (12) involves two terms with negative coefficients because ρ ∈ [−1,1] and σ, vj, and Si are positive. The existence of these terms with negative coefficients does not allow the technique developed in [18–20]. This fact motivates the transformation of problem (3) into an equivalent one where the mixed spatial derivative term disappears.

Firstly, we eliminate the reaction term rU by means of the substitution
()
obtaining
()
Now, following the classical techniques for reduction of second-order linear partial differential equations in two independent variables to canonical form, see for instance chapter 3 of [21], we proceed to classify the right-hand side of (14) by means of the sign of the discriminant
()
where
()
Under the assumption of correlated variables with −1 < ρ < 1, (14) becomes of elliptic type and the suitable substitution for eliminating the mixed spatial derivative term is given by solving the following ordinary differential equation:
()
where
()
Solving (17) one gets the following:
()
where the integration constant Z0 is related to the new variables by
()
From (19) and (20), it follows the expression of the new variables
()
By denoting W(x, y, τ)  =  V(S, v, τ), (14) takes the following equivalent elliptic form:
()
where v from (21) takes the expression in terms of x and y, given by the following:
()
It is important to remark that the previous substitution has also computational advantages because the elimination of the mixed derivative saves four terms using the same discretization scheme; see the last term of the right-hand side of (12).
Note that from (21), (4) the domain of the transformed problem (22) one gets the following:
()
and v means the variance of an underlying asset that must be positive, from (23) it follows that ; thus,
()
Thus, the domain of the transformed problem is as follows:
()
In the following we will assume that , because when m = 0, ρ = 0 and variables S and v are uncorrelated and the cross-derivative term disappears in (3).
Note that after substitution of (21) the final condition (5) of problem (3) takes the following form:
()
The boundary conditions (6), (9) of problem (3) are transformed into the following Dirichlet conditions:
()
()
and the boundary condition (7) is transformed into the following Neumann condition:
()
Boundary condition (8) can be replaced with a more practicable homogeneous Neumann condition:
()
see, for instance, [11, 13]. This boundary condition is transformed into the condition
()

Remark 1. In the next section, in order to introduce a numerical scheme, we will need to determine a bounded numerical domain.

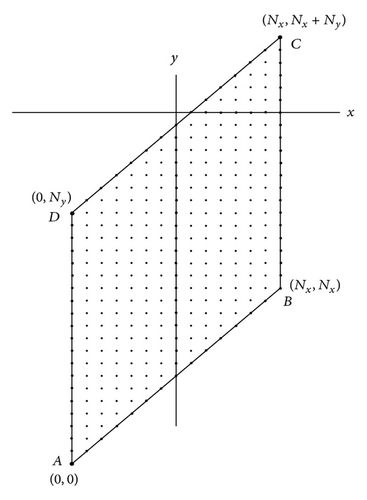
Because of the transformation of the spatial variables (21), a rectangle [S1, S2]×[v1, v2] is transformed into the rhomboid ABCD; see Figure 1, where the sides are described by the following:

()

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Rhomboid ABCD.

Remark 2. For the case |ρ | = 1, fully correlated variables S and v, from (15), the discriminant Δ = 0, and (14) become a parabolic PDE. Following the techniques for reduction to canonical form, an appropriate substitution is x = S; y = v − ρσln S and the transformed equation takes the following form:

()
where |ρ | = 1 and v = y + ρσln x.

3. Numerical Scheme and Boundary Numerical Domain Considerations

Dealing with numerical solutions using finite difference schemes requires the selection of our numerical domain and the transfer of the analytic boundary conditions of the problem to the boundary conditions of the numerical domain avoiding artificial behaviour of the numerical solution [22]. Unlike the classical stepsize discretizations, due to the transformation (21) and Remark 1, we use a discretization of the numerical domain where the stepsize discretizations are related by the slope appearing in (25). Thus, we guarantee that the rhomboid boundary of our numerical domain includes meshpoints of the discretization.

From [23, 24], a suitable bound for the underlying asset variable S is available and generally accepted. In an analogous way, considering an admissible range of the variance v, we can identify a convenient-bounded numerical domain [S1, S2]×[v1, v2] in the Sv plane.

In accordance with (33), let xi ∈ [a, b], with xi = a + ih, 0 ≤ i ≤ Nx,   Δx = h = (b − a)/Nx. Let Ny = (v2 − v1)/mh and yj ∈ [ma − v2, mb − v1] of the form
()
Once i is fixed, the admissible values of j so that (xi, yi) belongs to the rhomboid ABCD are given by the following:
()
Note that with this discretization the boundary sides of the rhomboid are partitioned in the following way:
()

Thus, the rhomboid spatial domain together with its boundary contains (Nx + 1)(Ny + 1) mesh points. See Figure 1.

For the time variable τ, we consider the standard discretization
()
Hence, the numerical domain Ω is defined by the following:
()
Note that because of (23) the value of v at the spatial variables (xi, yj) is as follows:
()
Using centered differences approximations for the spatial partial derivatives of (22) and forward in time partial derivatives, the numerical scheme for the internal mesh points of the numerical domain takes the following form:
()
where
()
is the approximation of the exact solution W(xi, yj, τn) of (22) at the mesh point (xi, yj, τn) and operators Δx,   Δy,  ∇x, and ∇y are defined by the following:
()
where h1 and h2 are the stepsize spatial variables related by the following:
()
in our numerical domain Ω. In (41) time-dependent parameters are described by κn = κ(τn) and θn = θ(τn). Thus, for the internal mesh points, the scheme (41) can be written in an explicit five points stencil scheme, (see Figure 2):
()
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Five-point versus nine-point stencils.
where
()
Finally, it remains translating the initial condition (27) and the boundary conditions (28)–(32) of the transformed problem (22), to the numerical domain. The initial condition gives the following:
()
The Dirichlet conditions (28)-(29) are translated to the numerical boundary as follows
()
along the side AD of the rhomboid, and
()
along the side AB of the rhomboid. The Neumann boundary conditions are translated by replacing the partial derivatives values for the corresponding finite differences approximations values.
So, condition (32) takes the discretized backward form in order to involve mesh points of the numerical domain:
()
or
()
The Neumann boundary condition (30) related to the numerical boundary BC of the rhomboid is regarded assuming that option price has a linear behaviour for large values of S. Hence, second partial derivatives terms vanish in (14) and taking into account the leading first partial derivative term of (14) for large values of S, one gets the following:
()
From (52), the change of variables (21), and (30), it follows that the boundary numerical condition for the BC side of the rhomboid is as follows:
()

Summarizing, the numerical scheme is expressed by (45) for the internal mesh points, together with the initial condition (47) and the boundary conditions (48)–(51) and (53).

4. Consistency

Let be the approximating difference equation (41). In accordance with [25, page 100], the scheme (41) is consistent with (22) if
()
where denotes the theoretical solution of (22) evaluated at (xi, yj, τn) and L is the operator:
()
Assuming that W is four times continuously differentiable with respect to x and y and twice with respect to τ, and using Taylor expansion about (xi, yj, τn) it follows that
()
where
()
()
With respect to the approximations of the spatial partial derivatives, let us denote
()
where
()
()
Analogously
()
where
()
()
Otherwise,
()
where
()
()
Let us write
()
where
()
()
From (56), (59), (62), (65), and (68), the local truncation error takes the following form:
()
From (58), (61), (64), (67), (70), and (71), one gets the following:
()

Summarizing, the following result has been established.

Theorem 3. Assuming that the exact solution W of (22) admits four times continuous partial derivatives with respect to the spatial variables x and y and twice continuous partial derivatives with respect to τ, the scheme (41) is consistent with (22) and the local truncation error behaves

()

5. Positivity and Stability

We begin this section showing that under suitable relationship between the stepsize discretizations, the coefficients of scheme (45) are nonnegative. This fact together with the positivity of the boundary values will guarantee the positivity of the values of the solution in all time steps at every spatial mesh point.

Let us start considering the first coefficient of the right-hand side of (45). Note that 1 − (k/h2)αi,j ≥ 0 is equivalent to the following condition:
()
Now, from (45) and taking into account that v1 ≤ vi,j ≤ v2, it follows that
()
Hence, (74) holds if
()
Note that the simultaneous nonnegativity of coefficients (ρ2/2h)αi,j + βi,j and (ρ2/2h)αi,j − βi,j is equivalent to the condition
()
From (46), condition (77) is equivalent to
()
Note that if r = (1/2)vi,j, condition (78) holds true. If r ≠ (1/2)vi,j, then let us write (78) in the following form:
()
As the minimum of real function in the interval 0 < z1 ≤ z ≤ z2 is given by
()
then from (80), condition (79) holds true if
()
Note that the simultaneous nonnegativity of coefficients and is equivalent to the condition
()
For the sake of clarity, let us introduce the following:
()
From (46) and (83), condition (82) can be written in the following form:
()
Note that if A(τn) = B(τn)vi,j, then (84) holds true. If A(τn) ≠ B(τn)vi,j, then (84) is equivalent to
()
As the continuous positive function
()
is bounded, in the compact [0, T]×[v1, v2], thus
()
From (85) and (87), condition (85) holds true if
()
Summarizing, the following result has been established.

Lemma 4. Let ha, hb be defined by (81) and (88), respectively, and let h0 = min {ha, hb}. Then, for h < h0 and k satisfying (76), all the coefficients of scheme (45) are nonnegative.

The nonnegativity of the coefficients of scheme (45) is not sufficient to guarantee the positivity of the constructed numerical solution due to the influence on the values at the boundaries of the numerical domain. From (47)–(51), (53), and Lemma 4 it is easy to show the positivity of in all the boundaries of the rhomboid for all n. Hence, the following result has been established.

Theorem 5. Let (xi, yj, τn) be a mesh point in the domain described by Ω (39) with a ≤ xi ≤ b,   v1 ≤ mxi − yj ≤ v2. Let be the numerical approximation of W(xi, yj, τn) given by (45) together with the initial condition (47) and the boundary conditions (48)–(51) and (53). Assume that h < h0, where h0 is given by Lemma 4, and k satisfying (76), then for all n, i, j.

The next result is a local discrete maximum principle that guarantees the boundedness of the numerical solution at the internal mesh points of the domain and that will be used below to prove the stability of the scheme.

Lemma 6. Let (i, j) be spatial internal mesh point with 1 ≤ i ≤ Nx − 1;     i + 1 ≤ j ≤ Ny + i − 1 and let be the pentaset

()

Then under conditions of Lemma 4, it follows that

()

for 0 ≤ n ≤ Nτ − 1.

Proof. From (45), Lemma 4, and using that and that the sum of all the five coefficients of the right-hand side of (45) is one, the result is established.

We conclude this section by introducing a concept of stability for the numerical solution of scheme (45), (47)–(51), (53). Let be the numerical solution of scheme (45), (47)–(51), (53) and consider the matrix wn in defined by
()
whose entries are the values of the numerical solution of the scheme for a fixed temporal step n.

Definition 7. With previous notation, we say that the solution of the scheme (45), (47)–(51), (53) is ∥·∥1-stable, if for small enough values of h1 = h = Δx, h2 = mΔx and k = Δτ, there is a constant M, independent of n, h, and k, such that

()
for all n such that 0 ≤ n ≤ Nτ, with kNτ = T.

Note that under conditions of Theorem 5, the entries of matrix wn are nonnegative and let us denote
()
Now, we show using induction principle that there exists a number sequence so that
()
Let us denote
()
and for n = 0, let us take Q0 = β; then from the initial condition (47) one gets the following:
()
If n = 1, for the internal mesh points, from Lemma 6, one gets the following:
()
From (48)–(51), and (53) and Theorem 5, since erk > 1 + kr for kr > 0, it follows that
()
Hence, taking Q1 = βerk, it follows that
()
Let
()
and assume the induction hypothesis
()
From Lemma 6, Theorem 5, and (48)–(51), and (53), one gets the following:
()
Thus, (100)-(101) holds true for n + 1. Note that 0 ≤ n ≤ Nτ,   k = T/Nτ, and using (100)-(101) one gets the following:
()
Let q be the positive number, 0 < q < 1, defined by . Note that from (47) and definition of ∥·∥1 one gets the following:
()
and from (103),
()
Finally, from (104)-(105)
()

Summarizing, the following result has been established.

Theorem 8. Consider the schemes (45), (47)–(51), (53) in the numerical domain Ω defined by (39) where , and yj ∈ [ma − v2, mb − v1],   τn ∈ [0, T]. Let h0 be defined by Lemma 4 and suppose that h = Δx < h0 and k = Δτ is small enough so that condition (76) is satisfied. Then the scheme is ∥·∥1-stable and

()

6. Examples and Simulations

In this section, we illustrate the good properties of the proposed numerical scheme. Firstly, we consider an example where the closed form solution is available.

Example 1. Consider the European call option for the Heston model (3).

E = 100; T = 1 year; r = 0.01; κ = 2; θ = 0.01; σ = 0.1; ρ = 0.5, v1 = 0.4, and v2 = 0.9.

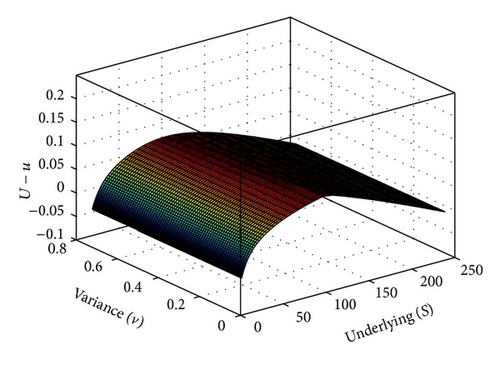
The difference between the closed form solution U and the numerical solution u is shown in Figure 3, by respecting the stability condition (76) and Lemma 4.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Error of numerical solution.

The following example shows the variation of the absolute and relative error of the numerical solution in light of the stability and positivity conditions hold at the strike for a given variance for different values of the stepsize discretizations h and k, respectively.

Example 2. Consider the European call option for the Heston mode (3) with data of Example 1 at S = E = 100,  v = 0.5. Table 1 shows the behaviour of the error with parameters h and k. Notice that the numerical solution exhibits the expected second order convergence rate in space. Analogously, for fixed h = 0.1 one gets convergence time rate of 0.97. For h = 0.05 the rate is 1.

Table 1. Errors and convergence rates.
  k = 0.015 k = 0.0075
  h 0.1 0.05 0.1 0.05
|U − u| 0.06056 0.01594 0.03079 0.00797
Convergence rate 1.93 1.95
Relative error 2.3 × 10−3 1.7907 × 10−4 1.2 × 10−3 8.9537 × 10−5

In the next example, we illustrate the fact that if we do not respect the stability condition, the numerical results are bad and unreliable.

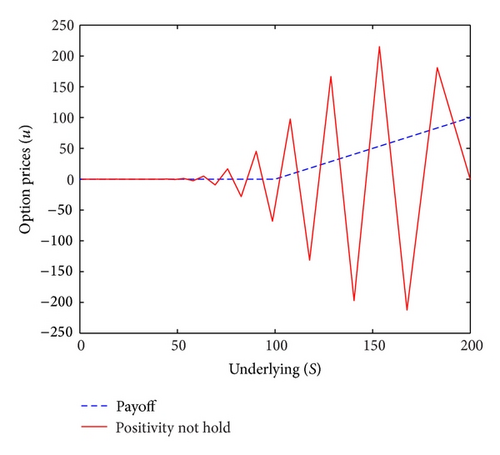
Example 3. Consider the problem of Example 1 at v = 0.9 with h = 0.0082, k = 0.0065, not verifying the stability condition (76). Figure 4 shows that spurious oscillations of the numerical solution appear when the stability condition is broken.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Breaking positivity and stability conditions.

The next example shows the dependence of the option price on both the underlying asset and the variance.

Example 4. Consider the European call option for the Heston model with data.

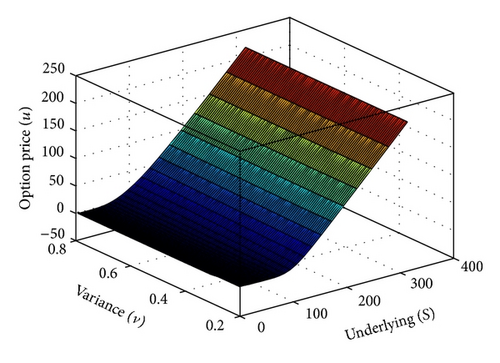
E = 100; T = 1 year;  r = 0.01;  κ = 2;  θ = 0.01;  σ = 0.1;  ρ = 0.4 and v1 = 0.2, v2 = 0.9. Figure 5 shows the numerical solution in 3D.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Numerical solution in 3D.

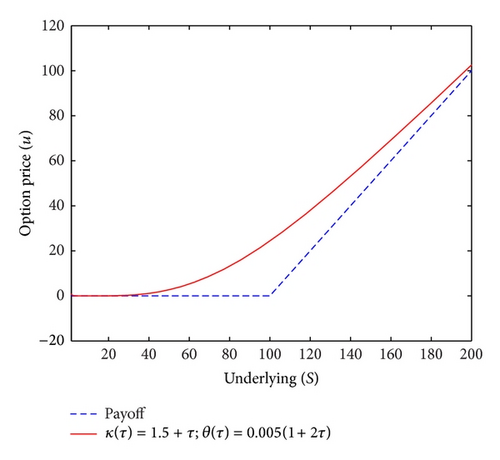
Finally, in the next example, we show the numerical result of a situation with time dependent mean reversion rate κ(τ) and long run variance θ(τ).

Example 5. Consider the European call option for the Heston model with data: E = 100; T = 1 year; r = 0.01; σ = 0.1; ρ = 0.4 and v1 = 0.4, v2 = 0.9 with time-dependent parameters κ(τ) = 1.5 + τ; θ(τ) = 0.005(1 + 2τ). Figure 6 shows the numerical results in this time-dependent case for v = 0.9.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
A time-dependent case.

Acknowledgments

This work has been partially supported by the European Union in the FP7-PEOPLE-2012-ITN Program under Grant Agreement no. 304617 (FP7 Marie Curie Action, Project Multi-ITN STRIKE-Novel Methods in Computational Finance) and by the Spanish MEYC Grant DPI2010-20891-C02-01.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.