Verification of Mixed-Signal Systems with Affine Arithmetic Assertions

1. Introduction

Analog/mixed-signal (AMS) systems are a crucial part of today’s embedded systems. Typical AMS components such as sensors, transceivers, and signal conditioning enable interaction of embedded HW/SW systems with its physical environment. In today’s embedded systems, the functionality of the analog components is tightly interwoven with the digital HW/SW system. A particular challenge of AMS systems is that parameters cannot be assumed to be fixed to a deterministic value like in a digital system.

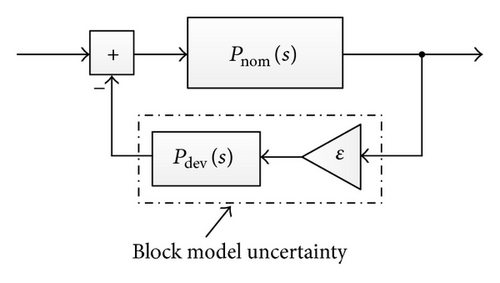
Behavior of AMS systems cannot be assumed to be fixed for the following reasons: variations of parameters due to variations in the manufacturing process, but as well during operation (e.g., different temperatures, aging, and supply voltage) introduce deviations compared to an ideal reference. (Modeling) uncertainties are introduced by the fact that all models represent more or less accurate abstractions of physical reality. No model can be assumed to be absolutely accurate. Furthermore, computation with fixed-point arithmetic in the digital domain can contribute significantly to deviation from expected ideal behavior (rounding errors, quantization). In the following we refer to such deviations of a simulation run from possible real behavior in general as “deviations.”

We mostly focus on level of block diagrams, but the methodology is as well applicable on circuit simulation. We implemented it based on SystemC and its AMS extensions. Section 2 gives a review of state of the art and related work. In Section 3 Affine Arithmetic is described, and some modeling examples are given. Section 4 describes semisymbolic simulation and the verification method proposed in this work. The applicability of the verification technology is demonstrated by examples given in Section 5. Section 6 concludes the paper and identifies future work.

2. State of Art and Related Work

When verifying AMS systems with parameter deviations, application of multirun simulation techniques (Monte-Carlo, worst-case analysis) can be considered as state-of-the art. Monte Carlo simulation [1] is a statistical technique. However, statistical techniques do not provide dependable “worst case” results. While the number of simulation runs can be reduced by importance sampling [2], the number of simulation runs required may still be prohibitive for analysis of complex systems. Corner case analysis [3] is a more appropriate means for finding worst case performances of AMS systems. Unfortunately, the number of simulation runs grows exponentially with the number of parameters considered. However, even if all corner cases are considered, the dependability of the result cannot be guaranteed since corner cases are not necessarily worst cases. Design of Experiments [4] allows reducing the number of simulation runs significantly and finding worst case performances more accurately.

Even with high number of simulation runs, there is no guarantee that worst case performances are found. A drawback of multi-run simulation methods is that the dependable operation of AMS systems cannot be guaranteed under all circumstances. For safety-critical systems, for example, in aviation or automotive systems this is a major drawback and motivation for further research.

In order to find counter examples, rapidly exploring random trees [5, 6] and robust test case generation have been proposed in [7–9]. Further, the simulation techniques proposed in [10, 11] guarantee that a system is “safe” if a set of trajectories lie within certain regions defined by previously found conditions. In contrast to these approaches the techniques proposed in [12, 13] compute an overapproximation of the set of states reached by all trajectories. While these methods support debugging and introduce coverage metrics, they are not able to deal with the increased complexity of systems that with deviations and variations. An approach that enables safety verification of hybrid systems with uncertain parameters is the use of barrier certificates proposed in [14]. Those methods can verify if a set of system trajectories crosses a barrier previously defined by a barrier certificate. Finding a proper barrier certificate is not easy and makes this approach difficult for system verification.

To cope with the drawbacks of simulation-based techniques, formal verification methods were proposed. The idea of formal methods is to use the formal checkers which automatically explore all possible states and transitions in the system model to check if the desired output behaviour is met or not. Hence, in contrast to simulation-based methods which can verify only one behaviour (for only one input stimuli) per operation, the formal methods deal with the set of behaviours at a time. Approaches for formal verification were firstly applied on digital systems [15–17], and due to their efficiency they found a good way in industrial applications. Approaches that also cover analog/mixed-signal or hybrid systems are rare and still in infancy.

In [18–20] hybrid systems with linear and nonlinear dynamics are approximated by timed automata in order to simplify their analysis. Reference [21] describes a model checking tool which requires discrete and (for continuous parts) linear system descriptions. For nonlinear continuous behavior, such approximations are too simple. Linear phase-portrait approximation [22] is a general technique, because its approximation does not depend on the order of the differential equation to be approximated. There is no standard method for partitioning the state space, and therefore it seems to be complicated to find proper discrete models for strongly nonlinear models. In [23–25] focus is on nonlinear analog behavior for which discretized models in the state space are used for verification. The efficiency of these approaches seems to be limited to smaller analog systems. With increasing complexity, the number of states in the discretized model grows which leads to the state explosion problem and high run time of verification algorithms applied on this model.

Due to limitation of formal methods for analog/continuous systems to small systems, simulation-based techniques are still the only way for verification of more complex analog/continuous and AMS systems. To formalize verification of AMS systems, assertions that describe typical properties of analog systems are the focus of recent research. In [26] mixed-signal assertions (MSA) were proposed to check properties of mixed-signal systems during simulation. These assertions were implemented in a separate SCAC (SystemC AMS Temporal Checker) library. This library is easily integrated in SystemC AMS simulation environment, due to its C++ based nature. In contrast to this approach, [27] features AMT, an offline tool for monitoring temporal properties of mixed-signal systems for verification. Both verification methodologies simulate and evaluate a nominal system model without taking into account any deviations caused by variations in design process.

A particular challenge in design of complex analog/mixed-signal systems is parameter variations. In any physical system, values are not implemented in an accurate way and change in a partially unpredictable way over time (e.g., due to temperature, aging, etc.). Such deviations form an ideal model change system behavior and can potentially cause malfunctions. For conventional simulation, multi-run methods as described in the first paragraph do not provide the result dependability and require a high number of simulation runs to explore the system behaviour while considering process variations. For formal approaches, such issues are still in infancy, because its applicability simply does not yet allow handling complex and heterogeneous systems such as AMS systems.

A first approach to cover deviation effects in AMS systems and compute the guaranteed worst case results at the same time was introduced in [28–31]. Deviations are modeled as ranges, superimposed on the nominal system model, and modified during system simulation to obtain the formally guaranteed range-based system quantities. For this purpose, Affine Arithmetic was applied. Using this approach the variations in parameter values are represented with deviated symbols which are traced to the system output. Hence, the contribution of all variations in the system is contained in the system response which simplifies analysis of the system robustness.

In [32] it is proposed that how Affine Arithmetic approach can be used to analyze worst case behavior of electrical circuits. Further, in [33] this methodology found its application in sizing of analog circuits. Using Affine Arithmetic the bounds on the worst case circuit behavior are calculated and the global minimum of sizing problem is determined due to inclusion isotonicity. Beside analog domain, Affine Arithmetic models can also be used in Digital Signal Processing (DSP) applications to represent errors introduced by calculations in floating-point arithmetic [34, 35].

Within this work, semisymbolic simulation based on Affine Arithmetic is combined with the assertion-based technology. Concretely, assertions based on Affine Arithmetic (AAF+A) are introduced to include range-based system quantities and allow specification and automatic verification of typical time and frequency-domain properties of systems considering variations in their parameter values.

Table 1 summarizes the advantages and disadvantages of previously described verification techniques.

The verification method proposed in this work copes with the disadvantages of previous verification methods. Concretely, combining the assertion-based technology with semisymbolic simulation, which generates the dependable guaranteed result in which all output values for the considered parameter set are contained, 100% coverage can be obtained.

3. Affine Arithmetic and Its Use for Modeling Deviations

3.2. Modeling Examples with Affine Arithmetic

In the following we show how to model different deviations. We focus on block-diagram like representations with transfer functions as common in control theory, because this model of computation is generally applicable to a vast set of different domains, including communication systems and electronic circuits. We focus on giving some mathematical background that can be applied in C-language (as in the examples in later sections), but as well, for example, in Matlab/Simulink.

(a) Simple Example—Modeling Gain Variation. To model a gain variation of a block (e.g., a low noise amplifier (LNA)) we assume that the exact gain value is not known but lies in interval [K_min, K_max]. The range for K  [K_min, K_max] can be modeled using Affine Arithmetic as follows:

$$ (4)

where K_nom and K_dev correspond to the center value of the range and the maximum absolute deviation from the center value, respectively. To model the gain variation in the SystemC AMS (used as a simulation environment in this work) that extended with an abstract data type AAF and some constructors for typical deviations, it is only necessary to call the constructor of the amplifier module with K_nom and K_dev as the second and the third argument. The first argument is always the name of the module. Therefore, the amplifier can be instantiated by the following line of code:

amp amp_(“amp_”, Knom, Kdev).

(b) Modeling (Parameter) Uncertainties. Modeling uncertainties are due to lack of capturing absolute accurate models of “real” behavior. In order to describe simple modeling uncertainties, a more general model is assumed in which the “real” behavior can be included by parameter variations. As simple example, the following transfer function of a system block will be supposed:

$$ (5)

Further, it will be supposed that the exact value of the parameter a is not known, but it is known that it lies in interval [a_min, a_max]. The range for parameter a can be modeled using Affine Arithmetic as

$$ (6)

where a_nom represents the midpoint of the range and a_dev the maximum absolute deviation from the midpoint. Now the transfer function P(s) can be expressed as

$$ (7)

where P_nom(s) represents the nominal model with the parameter value a_nom as follows:

$$ (8)

and P_dev(s) is the deviation function modeled as P_dev(s) = a_devs. The system block model with parameter deviation can be represented with the block diagram shown in Figure 2.

(c) Variation of Time Delay, Jitter. Time delays are often varying, even in digital systems (“jitter”). A time delay can be modeled by the following transfer function:

$$ (9)

where P_nom(s) models an ideal behavior of a block (without time delay) and τ represents a time delay for which it is supposed that its exact value is not known, but it is known that it lies in interval [0, τ_max]. The time delay causes deviation of the block from its ideal behavior P_nom(s). This deviation will be modeled using Affine Arithmetic. In order to do this the exponential function e^−τs will be approximated using the first-order Taylor polynomial:

$$ (10)

where τ_nom represents time delay in ideal conditions whose value is zero. The symbol τ_dev represents the maximum absolute deviation of time delay from its nominal value, and ε is a real number whose value lies in interval [−1,1]. Substituting τ_nom = 0 in the previous equation we get

$$ (11)

Since the approximation of the exponential function e^−τs with the first-order Taylor polynomial represents the linearization of e^−τs around τ_nom, this polynomial is actually tangent line on the function at point τ_nom, as it can be seen in Figure 3. Replacing e^−τs in (9) with this approximation the transfer function P(s) can be approximated with

$$ (12)

where P_nom(s) models the block ideal behavior and P_dev(s) models the deviation from the ideal behavior. The block diagram corresponding to this model is shown in Figure 4.

3.3. Abstraction of Accurate Model with Affine Arithmetic

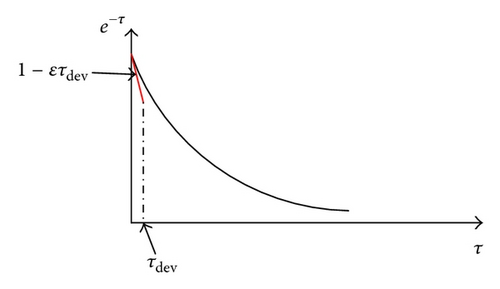
For verification of accurate system models in the presence of parameter deviations, a high number of simulation runs is required to achieve a sufficient verification coverage. To deal with this drawback “semisymbolic” approach based on Affine Arithmetic is introduced. Using this method an abstract system model is created in which the accurate system behavior is included. Concretely, abstraction of system model gets an overapproximation of accurate models and therefore gives a guaranty that if the abstract model satisfies desired specifications, the accurate model will also meet them.

To create the abstract model it will be supposed that there is a small change of the input voltage signal v_d around DC operating point (I_D, V_D) Δv_d (see Figure 5(b)). This change will be modeled using Affine Arithmetic as follows:

$$ (13)

The accurate model of a diode can be described with the following equation:

$$ (14)

To get the abstract model of a diode which is more simple for analysis, the accurate model will be approximated linearizing the nonlinear equation around DC operating point (I_D, V_D). This linearization will be performed using the first-order Taylor’s series as follows:

$$ (15)

where the symbol lin_error assigns linearization error which is added to enclose the accurate model in the abstracted one. The absolute value of this error represents the maximum absolute value of the Lagrange remainder:

$$ (16)

where ξ can take any value from ξ ∈ [V_D − Δv_d, V_D + Δv_d]. To include the accurate model, linearization error will be represented as

$$ (17)

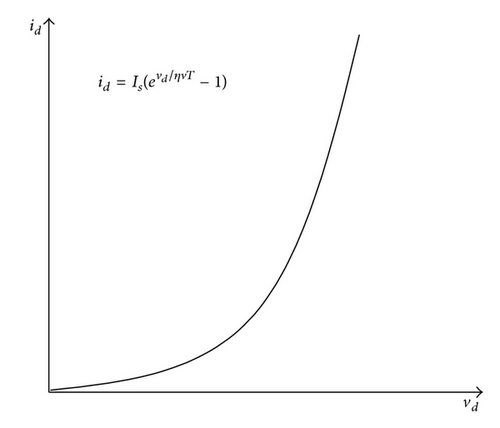
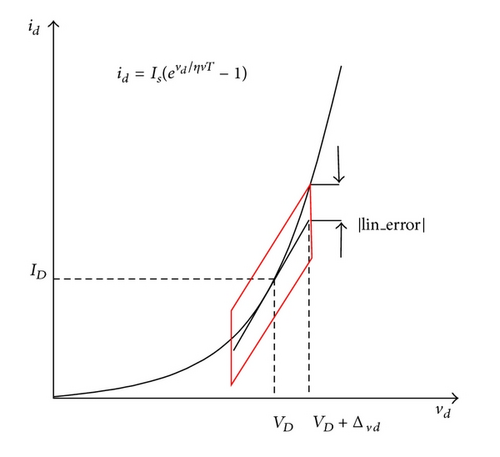
Figure 5(b) shows approximation of nonlinear diode (from Figure 5(a)) at the operating point.

4. Semisymbolic Simulation and Assertion-Based Verification

In order to reduce high number of simulation runs required for simulation of systems with parameter variations, semisymbolic simulation is introduced. The idea of this approach is to model parameter deviations using Affine Arithmetic and simulate systems including these deviations. The simulation result is range-based system response which can be obtained in only one simulation run. Semisymbolic simulation can be performed on two levels: system level and circuit level.

5. Demonstration Examples

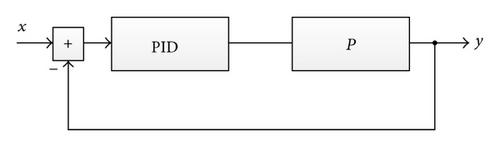
Within this work the applicability of the proposed verification method will be shown through several examples. The examples are chosen to demonstrate ability to handle typical challenges for symbolic simulation like feedback, nonlinearities, and discontinuities. Note that complexity itself is not a challenge by itself. As the first example a closed loop control system composed of a PID controller and a plant is chosen. Its block diagram is shown in Figure 6. Further, as the second example also a feedback system, which needs to set a room temperature to a certain value considering variation in the external temperature, is chosen. The third example through which the performance of the method will be illustrated is a PLL (Phase-Locked Loop) circuit containing the loop and nonlinear elements like a phase detector or a voltage controlled oscillator.

5.1. A Control System including a Parameter Uncertainty of a Plant

For the control system from Figure 6 a plant with the following transfer function will be considered:

$$ (24)

where for the parameter a it will be supposed that it lies in the interval [0.4,0.8]. This range is modeled using Affine Arithmetic as a = 0.6 + ε0.2 where ε ∈ [−1,1].

Substituting the affine form of the parameter a, P(s) can be rewritten as

$$ (25)

where P_nom(s) = 1/(s² + 0.6s + 1) and P_dev(s) = 0.2s. For a PID controller model it is supposed that a noise filter for the derivative term is included, yielding to the following controller structure:

$$ (26)

where the proportional gain K_p is 1.8, the integral time T_i = 0.38 s, and the derivative time T_d = 0.095 s. Between the integral and derivative times the ratio of 4 (T_i = 4*T_d) is chosen. In [38] it is shown that this ratio is appropriate for many industrial processes.

In order to behave appropriately whether in time or frequency domain, it is required for a control system to satisfy the certain number of specifications. One of the most important specifications on control systems is the stability of the closed loop system. The gain and phase margin of the closed loop system are typical stability criteria. The gain margin is the maximum amount of the gain which is allowed to increase in the loop before a closed loop system becomes unstable, and the phase margin tells how much the phase lag must increase to make the system unstable. Since it is necessary to specify both margins to ensure appropriate behavior of a system, they can be replaced by a single parameter named the stability margin M_s. This parameter is defined as the shortest distance between the Nyqvist curve of the loop transfer function and the critical point −1. This distance is actually the inverse of the maximum sensitivity. The loop transfer function is determined with L(s) = C(s)P(s) where C(s) and P(s) are the controller transfer function and the plant transfer function, respectively. Mathematically, the stability margin can be expressed as

$$ (27)

where S(jω) = 1/(1 + L(jω)) is the sensitivity function. In particular, the sensitivity function represents the disturbances amplification at the output of the plant by the closed loop system. Recommended values for the stability margin M_s lie in the range of [0.5,0.75] [38].

Within this paper it will be verified if the control system meets the stability margin specification. In order to satisfy the stability margin specification the system stability margin must lie in the recommended range. This range representing the specification for M_s will be modeled with Affine Arithmetic:

$$ (28)

where $$ represents the center value of the specified range and δ represents the maximum absolute distance from the center value. Concretely, since the specified range is [0.5, 0.75], spec(M_s) is equal to

$$ (29)

Including the parameter uncertainty in the plant, the stability margin M_s can be rewritten as

$$ (30)

This equation expresses that for every frequency it is necessary to determine the shortest distance of the loop transfer function from the critical point −1. It is very easy to be seen that the shortest distance will be obtained for ε = 1, which corresponds to the lower bound of range 1 + C(jω)P(jω).

A control system including uncertainties meets the stability margin specification if its stability margin M_s lies in the range [0.5,0.75]. Since M_s is crucial to verify the control system against the given specification, the proposed verification method will use the system given in Figure 7 to calculate the stability margin M_s.

Using the proposed verification method the specification to be verified will be described with AAF+A assertion which will be verified during simulation run. In order to calculate the stability margin following Expression 4 the minimum value of |1 + C(s)P(s)| with respect to frequency will be determined. This value can be found using AAF+A frequency operator min. One has

$$ (31)

where h(t) represents the response of the system with transfer function 1 + C(jω)P(jω) (Figure 7) on Dirac impulse. The operator FFT assigns the Fast Fourier Transform, and N is the number of points for which the Fourier is calculated. In this work N will be set to 2048.

It is important to note that the values calculated by FFT operator are range-based values, because the uncertainty of the plant model is modeled with Affine Arithmetic. The infimum with respect to frequency can be determined as the minimum of all FFT frequency components min (FFT). The stability margin corresponds to the lower bound of the range representing min (FFT)  (ε = 1) (Expression 4). As it is said, in order to meet design specification, it is required from the control system that its M_s lies in the specified range spec(M_s). Using the proposed method this requirement can be written as AAF+A assertion which will be verified during simulation as follows:

$$ (32)

This assertion expresses that infimum with respect to frequency determined with min (FFT〈2048〉(h(t)) must always (assigned with operator G) lie in the range modeling the stability margin specification (0.625 + ε0.125) during simulation.

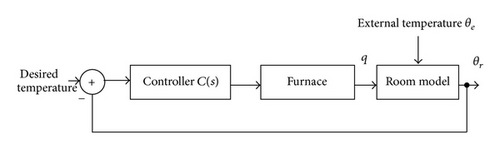
5.2. A Room Heating Control System

As the second demonstration example a system which controls a room temperature is chosen. The block diagram of the system is shown in Figure 8.

For room modeling the model including the thermal resistance of the wall between the room and the ambient R_ra, and the thermal capacitance of the room C_r is used. One part of heat, brought into the room, leaves the room through the resistor with R_ra and the other part is stored in the capacitor with thermal capacity C_r. This mathematical model can be described with the following equation:

$$ (33)

Using Laplase transformation the equation can be transformed into

$$ (34)

where q is the heat bringing into the system, θ_r is the temperature of the room, and θ_e is the external temperature. To determine the value of the thermal capacitance C_r, the certain number of factors needs to be considered (the heat capacity of the stuff in the room, the air in the room…). Within this work the value C_r = 10⁷ (J/K) is chosen (Appendix C in [39]). For the thermal resistance R_ra the value of R_ra = 0.0846*10⁻⁶ ( ^°C/W).

The controller used for this system is a PID controller with the following coefficients:

$$ (35)

According to (34) the room temperature θ_r can be calculated as

$$ (36)

For the external temperature θ_e it will be supposed that its value varies and lies in the range [−2,1]. This range will be modeled using Affine Arithmetic as

$$ (37)

Considering the variation in the external temperature it will be verified

• (1)

  if the room temperature θ_r within 5 seconds reaches the value varying within 3% of the final value,

• (2)

  if the final value is reached.

These two requirements will be described using Affine Arithmetic Assertions (AAF+A) and verified during simulation. The final value of the temperature is supposed to be 30^°C. The assertion corresponding to the first requirement can be written as

$$ (38)

where t_s is 5 s, θ_final is 30^∘C, and δ = 0.03*30 = 0.9 ^∘C and ε₁, ε₂ ∈ [−1,1]. The second requirement can be described with the following assertion:

$$ (39)

The simulation results are given in Table 5 in Section 5.4.

Table 5. Simulation results.

Example	Time without AAFA (s)	Time with AAFA (s)	Overhead (s)
The control system with parameter uncertainty	17.6	19.5	1.9
The room heating control system	9.3	10.8	1.5
PLL circuit	7.3	Simulation run stopped	—

5.3. A PLL Circuit including Parameter Uncertainties

As the second demonstration example a phased-locked loop (PLL) circuit is chosen. Due to high number of applications phased-locked loops found their place in analog-mixed-signal (AMS) systems. Some of these applications are listed in the following:

• (i)

  in radio transmitters it is used to synthesize frequencies, which are a multiple of a reference frequency;

• (ii)

  clock generators which multiply a low-frequency reference clock to higher operating frequencies of microprocessors;

• (iii)

  in communication systems for coherent demodulation and demodulation of frequency and phase modulated signals.

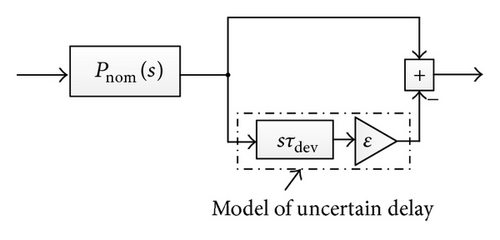
In this paper a PLL circuit as a frequency synthesizer is considered. Its block diagram is shown in Figure 9. This PLL model models the behavior of the system in ideal conditions. In reality certain numbers of deviations influence the behavior of the PLL causing design specifications to violate from their values previously defined by design. Since the PLL is often the part of more complex AMS systems (e.g., in the role as a frequency synthesizer it is embedded into communication systems to generate carrier frequencies) it is of a great importance to verify if the desired output behaviour in the presence of parameter deviations is still met. Within this work a time delay of the filter from Figure 9 will be considered and added to the PLL model.

As it can be seen from the figure the PLL model is comprised of a frequency detector, a filter, and a voltage controlled oscillator (VCO). The filter with the following transfer function is used:

$$ (40)

where K_f is the filter gain, and within this work it will be supposed that its value is one. For parameters a and b the values 2e⁻³ and 680*0.5*10⁻⁶ are supposed, respectively. The parameter τ represents time delay of the filter, and for this example it will be supposed that its value lies in the range [0,100 μs]. In Section 3.2 it is shown that time delay causes deviation from the nominal filter behavior approximating the filter transfer function H_f(s) with

$$ (41)

where H_f,nom represents the filter transfer function in ideal conditions (time delay τ is zero). Substituting the values for parameters K_f, a, and b, H_f,nom can be rewritten to

$$ (42)

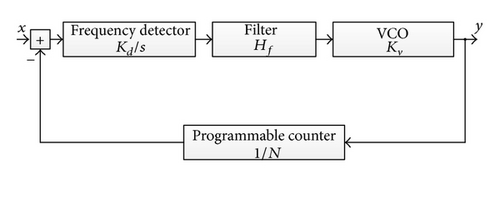
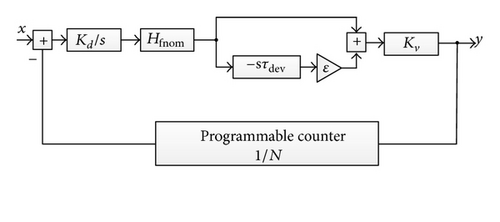
The parameter τ_dev represents the maximum value of time delay which is for this example 100 μs. The block diagram of the PLL model considering the filter time delay is shown in Figure 10.

For this PLL model it will be verified if the lock time of the PLL to switch from one frequency to within 5 kHz of another frequency is not greater than 1 ms. The PLL parameters such as f_step, the minimum obtained value of the output frequency f_o,min and the maximum obtained value of the output frequency f_o,max, are supposed to be 100 KHz, 2 MHz, and 3 MHz, respectively. The detector gain K_d and the gain of the voltage controlled oscillator K_v are supposed to be

$$ (43)

The loop gain of the system from Figure 10 is equal to

$$ (44)

From this formula it can be seen that for the maximum ratio of a programmable counter the loop gain will have the minimum value causing maximum lock time. Thus, only this ratio value will be considered. For considered PLL circuit this value is equal to

$$ (45)

Using the verification method proposed in this work the specification to be verified will be described with AAF+A assertion. This assertion will be verified during simulation as follows:

$$ (46)

where the values of ε₁ and ε₂ lie in the range [−1,1]. The operator F in the assertion assigns that the output frequency f_o must eventually within the settling time t_s enter the error band around the value of the steady state f_steady + ε₂δ and stay there (assigned with operator G).

We consider only the maximum ratio of the programmable counter, and therefore the frequency value in the steady state is f_steady = N*f_step = 30*100 KHz = 3 MHz. The other parameters are according to desired specification equal to

$$ (47)

Substituting these values in the previous assertion we have

$$ (48)

5.4. Experimental Results

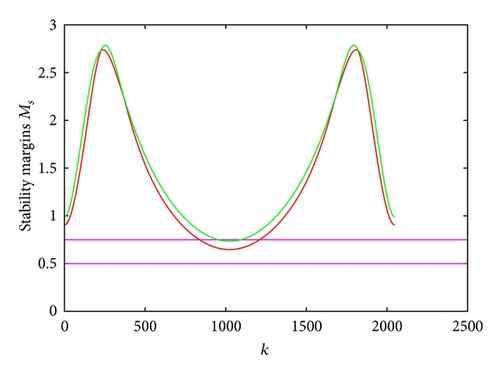
The SystemC AMS is used as simulation and verification environment. The control system considering the filter parameter uncertainty was simulated and verified for 10⁶ s with the sampling rate T_s = 1 s. The specification (Assertion 6) passed and the stability margin calculated for the control system is shown in Figure 11. The symbol k in the figure assigns the k frequency component of Fast Fourier Transform which was used to determine the stability margin with respect to frequency.

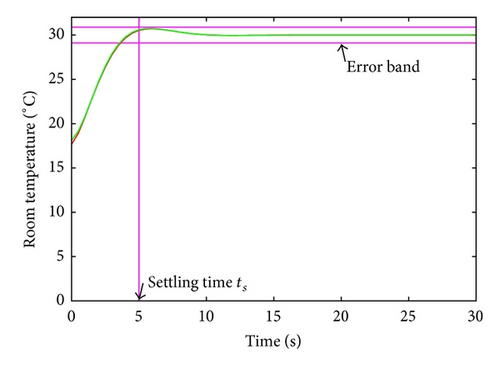
Using the sampling period T_s = 0.5 s the heating control system was simulated for 2*10⁵ s. The system met desired requirements and both assertions (Assertions 8 and 9) passed. The signal representing the room temperature θ_r is shown in Figure 11.

The PLL circuit was simulated and verified for 20 s with the sampling period T_s = 0.1 ms. It was verified if the lock time of the PLL to switch from 2.9 MHz to within 5 kHz of 3 MHz is less than 1 ms. The Assertion 10 failed, and simulation run was stopped reporting the information about the specification violation. The fact that the PLL output frequency did not (within 1 ms) set to the desired value within the specified tolerance does not imply that it will not do so after some time. To prove this the PLL simulation result is given in Figure 12.

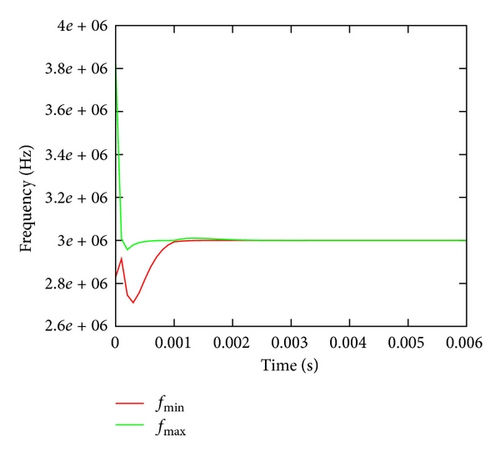
Since the assertion failed and the simulation run was stopped, the PLL response from Figure 12 is the result of simulation in the case where the assertion is omitted. From the figure it can be concluded that the output frequency converges to its final value and deviated terms converge to zero. This fact is one of the main advantages of the Affine Arithmetic approach. Its ability to identify the correlation between system quantities reaches its maximum in the systems with feedback loops like the case with our demonstration examples.

Hence, even in the case where the loop contains the nonlinear elements the additional terms (which are the result of overapproximation introduced by nonlinear operations) will have negligible values, and the output will converge to its finite value. To free the memory of unnecessary variables, the authors in [28] propose the (cleanup) method. Concretely, all terms under some user specified value are replaced with only two symbols, the one representing the sum of all terms with a positive and the other with a negative sign. In this way the safe inclusion of the result is kept, and the number of terms is drastically decreased.

Table 5 summarizes the simulation times necessary for all designs in the case where AAF+A assertions were included into design simulation and when they were omitted. It can be noted that in the case where the assertions were satisfied, the proposed verification method generated additional simulation time, but the overhead was not high.

The simulation time of the PLL in the case where the assertion was embedded into simulation was omitted. The reason lies in the fact that the assertion failed stopping the simulation process, and hence the time required for simulation was much lower than for the case in which the assertion was not included.

6. Conclusion and Future Work

This work introduces a methodology that enables verification of analog/mixed-signal systems including deviations. The verification method is combined with symbolic simulation which generates the worst case dependable response adding deviations to a system model and modeling them as ranges. Since the generated output behaviour contains all possible traces for the considered parameter set the proposed assertion-based technology can provide formal verification result using simulation-based techniques. The assertions use Affine Arithmetic to model allowed or forbidden areas of typical system properties as ranges. The specified ranges are further combined with Boolean logic, frequency operators, and temporal logic which allows us to verify the system behaviour in time, but also in the frequency domain. The assertions are embedded into simulation, and as soon as the assertion violation is detected, the simulation run is stopped, and information about the assertion harm is reported.

Overapproximation is a challenge that can become a problem for strongly nonlinear systems. The first step to deal with this problem was proposed in [28] and found its applicability in the systems containing the loops. The further step towards the problem solution is to modify Affine Arithmetic in the way that we keep the second order terms in symbolic representation and in this way that we reduce overapproximation.

Furthermore, the AAF+A assertions (Table 2) will be extended from rather formal operators to libraries of application-specific properties that are close to requirement specifications found in various application domains. Also, the method up to now verifies the system against the specifications for which time and frequency requirements must be known in advanced. One interesting direction in the future would be to extend the method to extract the information about lower and upper bounds of time or frequency for which the system behaviour is still desirable under the considered set of deviated parameters.