Multiple input multiple output-orthogonal frequency division multiplexing (MIMO-OFDM) with an electronically steerable passive array radiator (ESPAR) antenna receiver can improve the bit error rate performance and obtains additional diversity gain without increasing the number of Radio Frequency (RF) front-end circuits. However, due to the large size of the channel matrix, the computational cost required for the detection process using Vertical-Bell Laboratories Layered Space-Time (V-BLAST) detection is too high to be implemented. Using the minimum mean square error sparse-sorted QR decomposition (MMSE sparse-SQRD) algorithm for the detection process the average computational cost can be considerably reduced but is still higher compared with a conventional MIMOOFDM system without ESPAR antenna receiver. In this paper, we propose to use a low complexity submatrix divided MMSE sparse-SQRD algorithm for the detection process of MIMOOFDM with ESPAR antenna receiver. The computational cost analysis and simulation results show that on average the proposed scheme can further reduce the computational cost and achieve a complexity comparable to the conventional MIMO-OFDM detection schemes.

1. Introduction

In multipath fading channels, multiple input multiple output (MIMO) antenna systems can achieve a great increase in the channel capacity [1]. MIMO-OFDM combines the advantages of the MIMO systems with orthogonal frequency division multiplexing (OFDM) modulation, achieving a good performance for frequency selective fading channels. Due to these advantages, MIMO-OFDM allows high data rates in wireless communications systems. It is used in the wireless local area network (WLAN) standard IEEE 802.11n [2] and is also considered for the next-generation systems.

One of the limitations of MIMO-OFDM is that it requires one radio frequency (RF) front-end circuit for every receiver and transmitter antenna. Comparing MIMO-OFDM 2Tx-2Rx with MIMO-OFDM 2Tx-4Rx, MIMO-OFDM 2 × 4 can achieve better diversity gain and bit error rate performance but requires more RF front-end circuits, A/D converters, and FFT blocks for every additional branch.

In [3, 4] a MIMO-OFDM 2 × 2 scheme with electronically steerable passive array radiator (ESPAR) antenna receiver diversity has been proposed. It utilizes for every receiver a 2-element ESPAR antenna whose directivity is changed at the same frequency of the OFDM symbol rate. Compared to the conventional MIMO-OFDM 2 × 2 systems, this scheme gives additional diversity gain and improves the bit error rate performance without increasing the number of RF front-end circuits. For the detection the zero forcing (ZF) Vertical-Bell Laboratories Layered Space-Time (V-BLAST) algorithm [5, 6] is used but, due to the large size of the channel matrix, the required computational effort is very high.

In order to reduce the computational cost of the detection process of the scheme proposed in [3, 4], the use of a minimum mean square error sparse-sorted QR decomposition (MMSE sparse-SQRD) algorithm based on the SQRD algorithm introduced in [7, 8] was proposed by the authors in [9]. The computational cost reduction is achieved by exploiting the sparse structure of the channel matrix. This detection algorithm considerably reduces the average computational cost and also improves the bit error rate performance compared to the original scheme [3, 4]. A submatrix divided MMSE sparse-SQRD algorithm for the detection process of MIMO-OFDM with ESPAR antenna receiver was proposed by the authors in [10] for further reduction in the computational cost. This algorithm divides the channel matrix into k smaller submatrices reducing the computational cost but adding a small degradation in the bit error rate performance.

This paper is an extension of [10] including results of the bit error performance and computational cost for higher order submatrix division schemes. Also, another approach to further reduce the bit error degradation originated by the submatrix division algorithm is introduced.

The rest of this paper is organized as follows. Sections 2 and 3 gives a brief background description about OFDM and MIMO-OFDM with ESPAR antenna receiver. In Section 4, detection algorithms based on QR decomposition are shown. Then in Section 5 a detailed explanation about the MMSE sparse-SQRD algorithm is included. In Section 6 the proposed submatrix divided scheme is described. The computational cost analysis and simulation results are presented in Sections 7 and 8, respectively. And finally, in Section 9 conclusions are included.

2. OFDM with ESPAR Antenna

ESPAR is a small size and low power consumption antenna [11, 12]. It is composed by a radiator element connected to the RF front-end and one or more parasitic (passive) elements terminated by variables capacitances. The beam directivity can be controlled modifying the variables capacitances. This antenna requires only one RF front-end and therefore is known also as single RF port antenna array.

In [13] an OFDM receiver using ESPAR antenna is proposed. In this scheme the directivity of the ESPAR antenna is changed by a periodic wave whose frequency is the OFDM symbol rate. The block diagram of this scheme is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Block diagram of OFDM receiver with ESPAR antenna.

A two-element ESPAR antenna is utilized. The periodic variation of the directivity causes intercarrier interference (ICI) in the received signal. The ICI is caused by the addition of phase shifted components to the received signal. The frequency domain equalizer in Figure 1 uses both the shifted and nonshifted components in the detection. Due to this effect this scheme obtains diversity gain, therefore improving the bit error rate performance.

3. MIMO-OFDM with ESPAR Antenna Receiver

Based on [13], a MIMO-OFDM receiver with ESPAR antenna was proposed in [3, 4] and is described in this section. The block diagrams of the receiver and transmitter are shown in Figures 2 and 3, respectively.

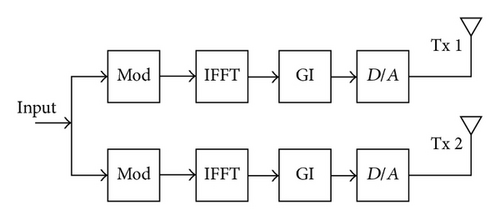
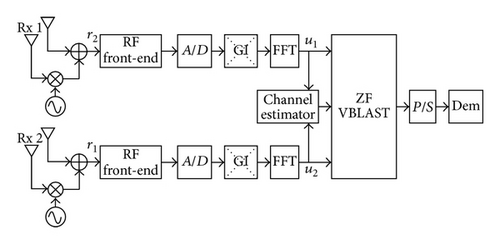
The transmitter is based on the WLAN standard IEEE 802.11n [2]. For simplicity forward error correction (FEC) interleaver blocks are not considered in the system. The receiver uses a 2-element ESPAR antenna where the directivity is also periodically changed according to the OFDM symbol rate. An MMSE channel estimator derived in [3, 4] is used and the detection process is carried out by the ZF V-BLAST detector.

3.1. Channel Estimation

For the channel estimation [13], let P₁ be the pilot symbol and its cyclic shifted P₂. The received signal after the FFT processor at the ith Rx is

(1)

where

and

are the channel response between the ith receive antenna and lth transmit antenna for the phase nonshifting (ns) and phase shifting (s) elements respectively. The matrix G represents the frequency shift due to directivity variation in ESPAR antenna and z is the additive white Gaussian noise (AWGN) vector.

From (1) the autocorrelation matrix

is given by

(2)

where

is the noise variance and R_h is the covariance matrix that represents the delay profile of the channel. Considering that the phase nonshifting (ns) and phase shifting (s) elements are spatially separated enough to be uncorrelated, the cross-correlation matrices B_i = E[uh^H] are given by

(3)

Using the MMSE criteria the channel response is given by

(4)

The channel matrix H has a size of 2(N + 2) × 2N, where N is the number of data subcarriers.

3.2. Detection

For the detection process the ZF V-BLAST [6] algorithm is used. In this algorithm the received signal vector is multiplied with a filter matrix G_ZF, that is, calculated by

(5)

where H^† is the Moore-Penrose pseudoinverse of H. The matrix G_ZF is calculated in a recursive way after zeroing one column of the channel matrix H; for this scheme the pseudoinverse is calculated 2N times. Due to the large size of the channel matrix H, calculating the pseudoinverse demands a very high computational effort and for this reason the detection process is the main limitation of this scheme.

4. QR Decomposition-Based Detection

Let x = [x₁, x₂, …, x_2N] ^T denote the vector of transmitted symbols, let z = [z₁, z₂, …, z_2(N+2)] ^T denote the vector of noise components and u = [u₁, u₂, …, u_2(N+2)] ^T the vector of received symbols.

4.1. MMSE-QRD

Applying like in [8] the MMSE detector criteria, let us denote the extended channel matrix

and the extended vector of received symbols

(6)

where σ_z is the noise standard deviation, I_2N is an identity matrix of size 2N × 2N, and 0_2N,1 is a column vector with 2N zero elements.

The QR decomposition of the extended channel matrix

can be expressed by

(7)

where

is a unitary matrix and

is an upper triangular matrix. And the extended vector of received symbols

is given by

(8)

Then (8) is multiplied by

to obtain

(9)

where

is the Hermitian transpose of

and

. The statistical properties of ν remain unchanged because

is a unitary matrix.

4.2. MMSE-SQRD

In [8] an MMSE sorted QRD detection algorithm based on the modified Gram-Schmidt algorithm is introduced. The starting condition is that ; then the norms of the column vectors of are calculated. For every step the column of with the minimum norm is found to maximize and the columns of are exchanged before the orthogonalization process. This algorithm calculates an improved matrix that reduces the error propagation through the detection layers. During the calculation, a permutation vector p carries the column exchanging operations for reordering the detected symbols at the end of the algorithm.

After the matrices and are calculated, then y is obtained according to (9) and the symbols are detected iteratively. After the symbols are detected, they are reordered using the permutation vector p to find the original sequence of the detected symbols.

5. MMSE Sparse-SQRD Algorithm

The extended channel matrix

whose size is 2(2N + 2) × 2N is shown in (10) and as we can see it is a sparse matrix. The MMSE sparse-SQRD algorithm is based on the MMSE-SQRD algorithm [8] and exploits the sparse structure of

to reduce the computational cost of the detection process:

(10)

Analysing given in (10) we can see that every column has only five nonzero elements so for the norm calculation of the column vectors of only these elements should be used. Also the positions of the nonzero elements are fixed so we have this information contained in a matrix as input. Using this information the norm calculation is shown in lines 5–9 of Algorithm 1.

Algorithm 1: MMSE sparse-SQRD.

1: Input: , Hnz
2: cols← # of columns of
3: rows← # of rows of
4: = 0, = , p = (1, …, cols)
5: for i = 1, …, cols do
6: for j = 1, …, 5 do
7:
8: end for
9: end for
10: for i = 1, …, cols do
11: k_i = arg min_l=i,…,cols norm_l
12: exchange columns i and k_i in , , norm, p
13:
14: nz ← indices of the non-zero elements of
15: for j = 1, …, length(nz) do
16:
17: end for
18: for l = i + 1, …, cols do
19: for j = 1, …, length(nz) do
20:
21: end for
22: if then
23: for j = 1, …, length(nz) do
24:
25: end for
26:
27: end if
28: end for
29: end for
30:
31:
32: for k = cols, …, 1 do
33:
34:
35: end for
36: Permutate according to p

In the orthogonalization process of the algorithm these two calculations

(11)

(12)

are performed in an iterative way.

denote the elements of the matrix

and

are column vectors of the matrix

In (11), the multiplication of the zero elements of the column vectors does not influence the final result so these multiplications can be avoided. A vector containing only the indices of the nonzero elements of the column vectors is obtained in line 14 so the number of operations required to calculate is reduced without influencing the final result. This is shown in lines 19–21 in the algorithm. The same strategy is used also in lines 15–17 and 23–25.

Also, due to the sparse structure of (10), the result of (11) can be zero. In this case calculating (12) is unnecessary because it does not change the value of so it can be avoided using the condition in line 22.

Also we can consider that the calculation of (9) can be simplified as

(13)

where Q₁ is a matrix with the same size of the channel matrix H. This is shown in lines 30-31 of the algorithm.

Using these analysed criteria the MMSE sparse-SQRD algorithm can achieve the same bit error rate performance of the MMSE-SQRD algorithm but with a considerable computational cost reduction.

6. Submatrix Divided Proposed Algorithm

In order to further reduce the computational cost of the detection process an algorithm based on submatrix division of the channel matrix is proposed. The block diagram of the proposed scheme is shown in Figure 4.

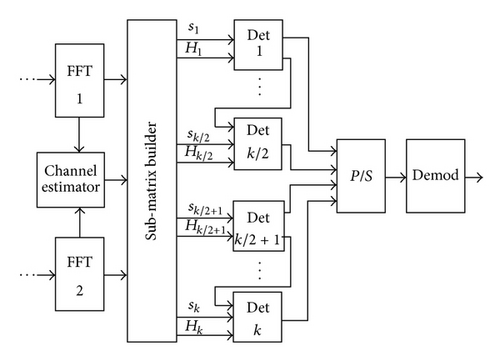
This detection scheme is composed by a submatrix builder block and k MMSE sparse-SQRD detectors. The submatrix builder is fed with the received symbols from the FFT processors and the channel state information obtained in the channel estimator. Its function is to build the submatrices and vectors for the detectors. Every detector is fed with a vector of received symbols s_i and a channel submatrix H_i.

From now on we consider the number of subcarriers to be N = 56 like in the IEEE 802.11n [2] standard. Let a = [a₁, a₂, …, a₅₈] ^T denote the vector of received (transmitted and interfered) symbols from the FFT1 processor and let b = [b₁, b₂, …, b₅₈] ^T denote the vector of received symbols from the FFT2 processor. For simplicity we consider that the extended channel submatrix is created inside the ith detector. Now we will explain in detail the submatrix division case when k = 4 considering two variations with 2 or 4-symbol overlapping.

6.1. Quarter-Size Submatrix (k = 4) with 2-Symbol Overlapping

In this case we divide the channel matrix into four submatrices denoted as H₁₂, H₂₂, H₃₂ and H₄₂. These matrices are shown in (14), (15), (16), and (17), respectively,

(14)

(15)

(16)

(17)

The vectors of received symbols applied to the four detectors are denoted as

(18)

And the vectors of detected symbols obtained from the detectors are denoted as

(19)

The submatrix division introduces a degradation in the bit error performance so now we explain the procedure used to minimize this effect. First the channel matrix nonshifted (ns) elements associated with the subcarrier −14 () are included in both H₁₂ and H₂₂. In the same way the nonshifted elements associated with the subcarrier +15 () are included in H₃₂ and H₄₂.

We overlap the symbols a₁₅, b₁₅ in vectors s_{1_2} and s_{2_2}. Using the information from the detection process of the detector 1, the symbols a₁₅, b₁₅ in vector s_{2_2} are compensated according to (20) where

represent the compensated symbols:

(20)

We also overlap symbols a₄₄, b₄₄ in s_{3_2} and s_{4_2}. The symbols a₄₄, b₄₄ in vector s_{4_2} are compensated according to (21) using the information of the detection process of the detector 3. Similarly

and

represent the compensated symbols:

(21)

During the sorting process of the detector 1, the columns containing the channel matrix nonshifted (ns) elements associated with the subcarrier −14 are used first regardless of its norm. It reduces the degradation introduced by these elements in the upper layers during the detection process. The same is performed in the detector 3 with the nonsubcarriershifted elements of the subcarrier +15.

In the vectors of detected symbols the overlapped detected elements x₁₅, x₇₁ in vector x_{1_2} and x₄₃, x₉₉ in vector x_{3_2} are discarded because they have a higher probability of error.

6.2. Quarter-Size Submatrix (k = 4) with 4-Symbol Overlapping

In this subsection another variation with 4-symbol overlapping is introduced. The objective of this idea is to further reduce the degradation in the bit error rate performance created by the submatrix division. Similar to the previous subsection we divide the channel matrix into four submatrices denoted as H₁₄, H₂₄, H₃₄, and H₄₄. These matrices are shown in (23), (24), (25), and (26), respectively. In this case the vectors of received symbols applied to the four detectors are denoted as

(22)

(23)

(24)

(25)

(26)

And the vectors of detected symbols obtained from the detectors are denoted as

(27)

In this variation 4 symbols a₁₅, a₁₆, b₁₅, b₁₆ in vectors s_{1_4} and s_{2_4} are overlapped. Similar to the previous subsection the symbols a₁₅, b₁₅ in vector s_{2_4} are compensated according to (20) using the elements of H₁₄ and x_{1_4}. We also overlap symbols a₄₄, a₄₅, b₄₄, b₄₅ in s_{3_4} and s_{4_4}. In the same way the symbols a₄₄, b₄₄ in vector s_{4_4} are compensated according to (21) using the elements of H₃₄ and x_{3_4}.

Also the channel matrix elements associated with the subcarriers −14 and −13 are included in both H₁₄ and H₂₄. In the same way the elements associated with the subcarriers +15 and +16 are included in H₃₄ and H₄₄. During the sorting process of the detector 1, the columns containing the channel matrix elements associated with the subcarriers −14 and −13 are used first regardless of its norm. The same is performed in the detector 3 with the elements of the subcarriers +15 and +16.

In the vectors of detected symbols the overlapped elements x₁₅, x₁₆, x₇₁, x₇₂ in vector x_{1_4} and x₄₃, x₄₄, x₉₉, x₁₀₀ in vector x_{3_4} are discarded because they have a higher probability of error.

7. Computational Cost

The computational cost is analysed in terms of the number of complex floating point operations (flops) ℱ required. As in [8], for simplicity we consider each complex addition as one flop and each complex multiplication as three flops. We cannot obtain a formula for the number of flops for the submatrix divided proposed algorithm because this number depends on the random sorting, so we obtained an average of the number of flops from the simulation results. Also, for comparison, the number of flops required by the ML detector [14] is

(28)

where M is the constellation size. The ZF-VBLAST algorithm like in [15] requires

(29)

where C is the number of columns and D is the number of rows of the channel matrix H.

In Tables 1 and 2 a computational cost comparison in terms of the average number of flops per subcarrier is presented for the case of 2- and 4-symbol overlapping, respectively. The tables show the number of flops per subcarrier for different submatrix sizes using different modulation schemes. The tables also include the number of flops for a full size channel matrix when the submatrix division scheme is not utilized. We can see that when the submatrix division order k increases the average number of flops per subcarrier is reduced. For the eighteen (k = 18) submatrix size, that is, the maximum achievable division of the scheme, we obtain the minimum average computational cost. Also we can see that the average number of flops is similar for the different modulation schemes. And, the number of flops for the 4-symbols overlapping option is bigger compared with the other 2-symbols overlapping option.

Table 1. Average number of flops per subcarrier of the proposed algorithm with 2-symbol overlapping.

Submatrix size	QPSK	16-QAM	64-QAM
Full w/o division	7005	6832	6751
Quarter (k = 4)	2645	2580	2552
Eighth (k = 8)	1078	1060	1050
Eighteenth (k = 18)	519	518	516

Table 2. Average number of flops per subcarrier of the proposed algorithm with 4-symbol overlapping.

Submatrix size	QPSK	16-QAM	64-QAM
Full w/o division	7005	6832	6751
Quarter (k = 4)	2792	2725	2696
Eighth (k = 8)	1277	1272	1269
Eighteenth (k = 18)	770	768	765

Table 3 shows as reference the number of flops per subcarrier of the conventional MIMO 2 × 2 VBLAST and MIMO 2 × 2 MLD both without ESPAR antenna receiver. Also the computational cost using eighteenth-size (k = 18) submatrix division MMSE sparse-SQRD algorithm with 2 and 4-symbols overlapping is included. We can see that the average number of flops per subcarrier of the proposed submatrix division based algorithm is similar to the flops of MIMO 2 × 2 VBLAST and better than MIMO 2 × 2 MLD scheme for 16-QAM and 64-QAM modulation.

Table 3. Flops per subcarrier comparison.

Algorithm	QPSK	16-QAM	64-QAM
MIMO 2 × 2 VBLAST w/o ESPAR	542	542	542
MIMO 2 × 2 MLD w/o ESPAR	312	4992	79872
(k = 18) with 2-sym overlapping	519	518	516
(k = 18) with 4-sym overlapping	770	768	765

For calculating the total computational cost required by the receiver, based on [16] the number of flops required by the two FFT blocks considering the data symbol and pilot symbol is

(30)

where N_FFT is the FFT size. Also the flops required by the channel estimator used for the ESPAR antenna receiver, that was presented in Section 3.1, are given by

(31)

Table 4 presents the total flops per subcarrier required by the receiver using QPSK modulation. Also the complexity of the FFT, channel estimator, and detection blocks is included for the different systems. The MIMO-OFDM systems that are analysed in this table are the original system with ESPAR antenna receiver using ZF-VBLAST detector [3, 4], the system using full-size channel matrix detection, the system using the proposed submatrix divided (k = 18) with 4-symbol overlapping detection and the 2 × 2 VBLAST system without ESPAR antenna receiver. We can observe that using the proposed submatrix divided scheme (k = 18) with 4-symbols overlapping the computational cost required for the detection and also the total number of flops per subcarrier required by the receiver are reduced.

Table 4. Total flops per subcarrier of the receiver using QPSK mod.

MIMO-OFDM system	FFT	Channel estimator	Detection	Total
ZF-VBLAST with ESPAR [3, 4]	70	1856	4.1 ×10⁷	4.1 ×10⁷
Full-size w/o division	70	1856	7005	8931
Proposed (k = 18) 4-sym. over.	70	1856	770	2696
2 × 2 VBLAST w/o ESPAR	70	173	542	785

8. Simulation Results

To determine the bit error rate performance of the proposed algorithm, a software simulation model of MIMO-OFDM with ESPAR antenna receiver was developed in c++ using the it++ [17] communications library. It is important to note that the system does not include FEC and interleaver. In the simulation the proposed low complexity submatrix divided MMSE sparse-SQRD detection is implemented with quarter-size, eighth-size and eighteenth-size, submatrices. Both options, with 2- and 4-symbol overlapping, are implemented for the previous mentioned submatrix sizes. The configuration settings of the simulation are shown in Table 5.

Table 5. Simulation settings.

	Modulation	QPSK, 16-QAM, 64-QAM
	Pilot sequence	HTLTF
Tx	Number of subcarriers	56
	FFT size	64
	GI	1/4
	Rayleigh fading	2 rays
Channel	Noise type	AWGN
	Bandwidth	20 MHz
Rx	Synchronization of symbols	Perfect
Rx	Channel estimation	MMSE

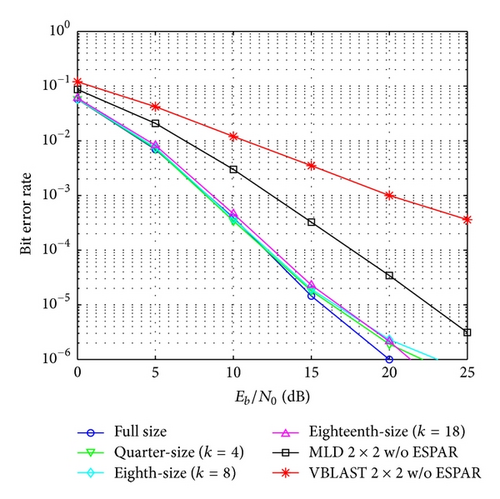
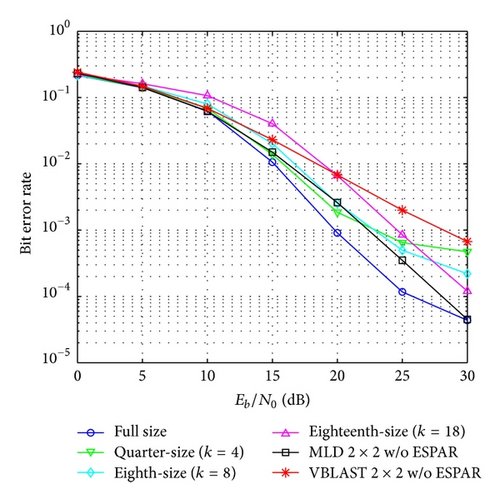
In Figures 5 and 6 the bit error rate performance using QPSK modulation, for the cases of 2- and 4-symbol overlapping, respectively, is shown. In these figures the performance of the proposed algorithm for quarter-size (k = 4), eighth-size (k = 8), and eighteenth-size (k = 18) submatrices is included. To compare the degradation in the bit error performance created by the algorithm, the performance in the case of a full-size channel matrix without division is included. And also the performance of conventional MIMO-OFDM 2 × 2 VBLAST and MIMO-OFDM 2 × 2 MLD systems without ESPAR antenna receiver is shown. As we can see in Figure 6, with QPSK modulation and 4-symbol overlapping, the bit error rate performance degradation is minimum even for the case of eighteenth-size (k = 18) submatrix size. Also for a BER of 10⁻³, the proposed scheme with eighteenth-size (k = 18) submatrix size that achieves the minimum computational cost obtains an additional gain of about 11 dB compared to a conventional MIMO-OFDM 2 × 2 VBLAST system without ESPAR antenna receiver.

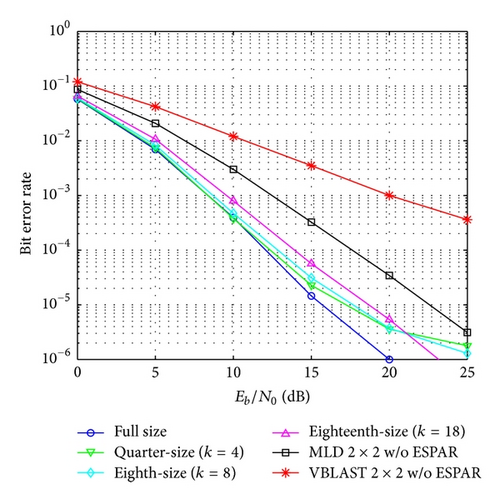
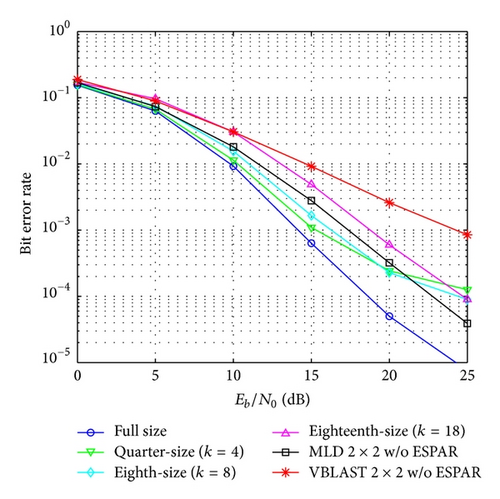
In the same way the bit error rate using 16-QAM modulation is shown in Figures 7 and 8. With 16-QAM modulation the degradation in the bit error rate performance is bigger compared with the QPSK results. In this case also the degradation is smaller in the case of 4-symbols overlapping. With 16-QAM for a BER of 10⁻³, the proposed scheme with eighteenth-size (k = 18) submatrix size, obtains an additional gain of about 8.5 dB compared to a conventional MIMO-OFDM 2 × 2 VBLAST system.

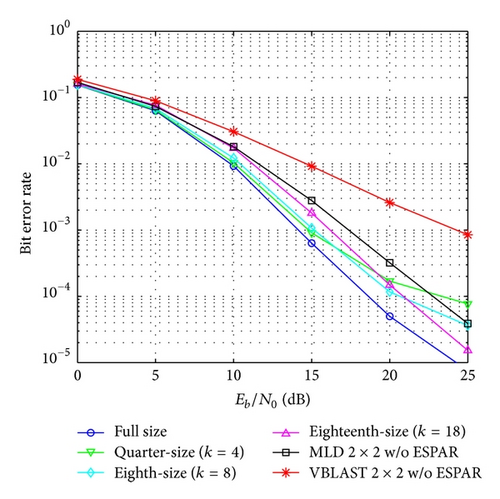
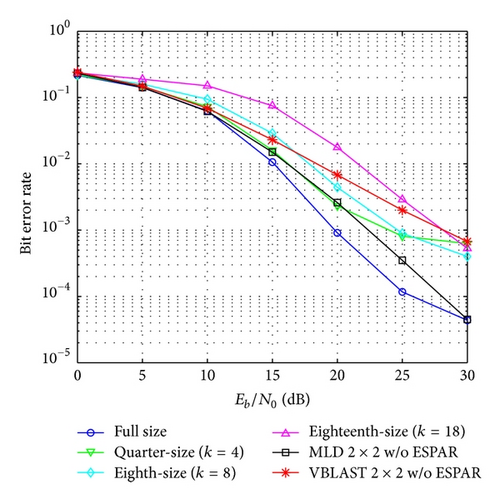
The results for 64-QAM are shown in Figures 9 and 10. In this case the degradation is much bigger and the best result is obtained with the 4-symbol overlapping option.

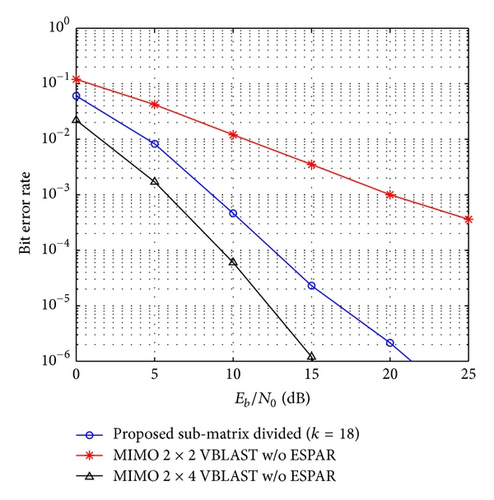
In Figure 11 the BER performance of the proposed submatrix divided (k = 18) scheme with 4-symbol overlapping is compared with the conventional MIMO 2 × 2 VBLAST and MIMO 2 × 4 VBLAST without ESPAR antenna using QPSK modulation. This is not a fair comparison in terms of the number of RF front-ends in the receiver side because MIMO 2 × 4 VBLAST requires four RF front-ends compared to MIMO 2 × 2 VBLAST and the proposed submatrix divided (k = 18) scheme that only require two RF-front ends. However, this figure shows that the proposed scheme cannot overcome the BER performance of MIMO 2 × 4 VBLAST without ESPAR antenna but gives a considerable improvement compared to the BER of MIMO 2 × 2 VBLAST without ESPAR antenna receiver. Also in this figure we can observe that the slope of the proposed scheme and MIMO 2 × 4 VBLAST are similar and steeper compared to MIMO 2 × 2 VBLAST. Therefore, our proposed scheme achieves a diversity order similar to MIMO 2 × 4 VBLAST without ESPAR antenna receiver.

9. Conclusion

In this paper, we have proposed a low complexity submatrix divided MMSE Sparse-SQRD algorithm for the detection of MIMO-OFDM with ESPAR antenna receiver. The computational cost analysis shows that this algorithm can further reduce the average computational effort achieving a complexity comparable to the common MIMO-OFDM detection schemes. We analysed two variations using 2- and 4-symbol overlapping. From the results the option with 4-symbol overlapping obtains the best performance in terms of bit error rate, yet increasing the computational cost compared with the other option. The proposed detection scheme is flexible, so the best trade-off between computational cost and bit error rate can be selected depending on the design constraints.

The main application of MIMO-OFDM with ESPAR antenna receiver is to improve the bit error rate performance and diversity gain without increasing the number of RF front-end circuits. And utilizing the proposed low complexity detection scheme we can obtain this improvement in the performance with a low computational cost. The proposed detection scheme is specifically designed to reduce the computational cost of the detection of MIMO-OFDM with ESPAR antenna receiver but it can be also applied in the detection of similar systems that have a large size channel matrix.

In future research we will work in the channel estimator because it is necessary to reduce its computational cost. Also, we will add FEC and interleaver to the system for further improvement in the bit error rate performance.

References

1 Telatar E., Capacity of multi-antenna Gaussian channels, European Transactions on Telecommunications. (1999) 10, no. 6, 585–595, 2-s2.0-0004083131.
Google Scholar
2 IEEE Computer Society, IEEE Standard for Information Technology Telecommunication and Information Exchange between Systems Local and Metropolitan Area Networks Specific Requirements, 2009, IEEE Computer Society, New York, NY, USA.
Google Scholar
3 Astawa I. G. P. and Okada M., ESPAR antenna-based diversity scheme for MIMO-OFDM systems, Proceedings of the 2009 Thainland—Japan MicroWave, February 2010, 1–4.
Google Scholar
4 Astawa I. G. P. and Okada M., An RF signal processing based diversity scheme for MIMO-OFDM systems, IEICE Transactions on Communications. (2012) 95, no. 2, 515–524, https://doi.org/10.1587/transfun.E95.A.515.
Google Scholar
5 Foschini G. J., Golden G. D., Valenzuela R. A., and Wolniansky P. W., Simplified processing for high spectral efficiency wireless communication employing multi-element arrays, IEEE Journal on Selected Areas in Communications. (1999) 17, no. 11, 1841–1852, 2-s2.0-0033352714, https://doi.org/10.1109/49.806815.
Web of Science® Google Scholar
6 Wolniansky P. W., Foschini G. J., Golden G. D., and Valenzuela R. A., V-BLAST: an architecture for realizing very high data rates over the rich-scattering wireless channel, Proceedings of the URSI International Symposium on Signals, Systems, and Electronics (ISSSE ′98), October 1998, 295–300, 2-s2.0-0032217929.
Google Scholar
7 Wubben D., Rinas J., Bohnke R., Kuhn V., and Kammeyer K. D., Efficient algorithm for detecting layered space-time codes, Proceedings of the ITG Conference on Source and Channel Coding, January 2002, Berlin, Germany, 399–405.
Google Scholar
8 Wubben D., Bohnke R., Kuhn V., and Kammeyer K. D., MMSE extension of V-BLAST based on sorted QR decomposition, 1, Proceedings of the IEEE 58th Vehicular Technology Conference (VTC ′03-Fall), 508–512, https://doi.org/10.1109/VETECF.2003.1285069.
Google Scholar
9 Reinoso Ch D. J. and Okada M., Computational cost reduction of MIMOOFDM with ESPAR antenna receiver using MMSE Sparse-SQRD detection, Proceedings of the 27th International Technical Conference on Circuit/Systems, Computers and Communications, July 2012, Sapporo, Japan.
Google Scholar
10 Chisaguano D. J. R. and Okada M., ESPAR antenna assisted MIMO-OFDM receiver using sub-matrix divided MMSE sparse-SQRD detection, Proceedings of the International Symposium on Communications and Information Technologies (ISCIT ′12), October 2012, Gold Coast, Australia, 198–203, https://doi.org/10.1109/ISCIT.2012.6380890.
Google Scholar
11 Ohira T. and Iigusa K., Electronically steerable parasitic array radiator antenna, Electronics and Communications in Japan II. (2004) 87, no. 10, 25–45, 2-s2.0-7244241010, https://doi.org/10.1002/ecjb.20081.
Google Scholar
12 Ohira T. and Gyoda K., Electronically steerable passive array radiator antennas for low-cost analog adaptive beamforming, Proceedings of the IEEE International Conference on Phased Array Systems and Technology, May 2000, Dana Point, Calif, USA, 101–104, 2-s2.0-0033713036.
Google Scholar
13 Tsukamoto S. and Okada M., Single-RF diversity for OFDM system using ESPAR antenna with periodically changing directivity, Proceedings of the 2nd International Symposium on Radio Systems and Space Plasma, August 2010, Sofia, Bulgaria, 1–4.
Google Scholar
14 Chouayakh M., Knopp A., and Lankl B., Low complexity two stage detection scheme for MIMO systems, Proceedings of the IEEE Information Theory Workshop on Information Theory for Wireless Networks (ITW ′07), July 2007, Solstrand, Norway, 1–5, 2-s2.0-47849111286, https://doi.org/10.1109/ITWITWN.2007.4318062.
Google Scholar
15 Benesty J., Huang Y., and Chen J., A fast recursive algorithm for optimum sequential signal detection in a BLAST system, IEEE Transactions on Signal Processing. (2003) 51, no. 7, 1722–1730, 2-s2.0-0038199781, https://doi.org/10.1109/TSP.2003.812897.
Google Scholar
16 Johnson S. G. and Frigo M., A modified split-radix FFT with fewer arithmetic operations, IEEE Transactions on Signal Processing. (2007) 55, no. 1, 111–119, 2-s2.0-33947416576, https://doi.org/10.1109/TSP.2006.882087.
Google Scholar
17 Welcome to IT++!, 2010, http://itpp.sourceforge.net/devel/index.html.
Google Scholar

Citing Literature

All articles

Low Complexity Submatrix Divided MMSE Sparse-SQRD Detection for MIMO-OFDM with ESPAR Antenna Receiver

Abstract

1. Introduction

2. OFDM with ESPAR Antenna