Volume 2013, Issue 1 187383

Research Article

Open Access

A Numerical Solution to Fractional Diffusion Equation for Force-Free Case

O. Tasbozan,

O. Tasbozan

Department of Mathematics, Faculty of Art and Sciences, Inonu University, 44280 Malatya, Turkey inonu.edu.tr

Search for more papers by this author

A. Esen,

A. Esen

Department of Mathematics, Faculty of Art and Sciences, Inonu University, 44280 Malatya, Turkey inonu.edu.tr

Search for more papers by this author

N. M. Yagmurlu,

Corresponding Author

N. M. Yagmurlu

[email protected]

Department of Mathematics, Faculty of Art and Sciences, Inonu University, 44280 Malatya, Turkey inonu.edu.tr

Search for more papers by this author

Y. Ucar,

Y. Ucar

Department of Mathematics, Faculty of Art and Sciences, Inonu University, 44280 Malatya, Turkey inonu.edu.tr

Search for more papers by this author

O. Tasbozan,

O. Tasbozan

Department of Mathematics, Faculty of Art and Sciences, Inonu University, 44280 Malatya, Turkey inonu.edu.tr

Search for more papers by this author

A. Esen,

A. Esen

Department of Mathematics, Faculty of Art and Sciences, Inonu University, 44280 Malatya, Turkey inonu.edu.tr

Search for more papers by this author

N. M. Yagmurlu,

Corresponding Author

N. M. Yagmurlu

[email protected]

Department of Mathematics, Faculty of Art and Sciences, Inonu University, 44280 Malatya, Turkey inonu.edu.tr

Search for more papers by this author

Y. Ucar,

Y. Ucar

Department of Mathematics, Faculty of Art and Sciences, Inonu University, 44280 Malatya, Turkey inonu.edu.tr

Search for more papers by this author

First published: 16 May 2013

https://doi.org/10.1155/2013/187383

Citations: 18

Academic Editor: Mustafa Bayram

Share a link

Email
Wechat
Bluesky

Abstract

A collocation finite element method for solving fractional diffusion equation for force-free case is considered. In this paper, we develop an approximation method based on collocation finite elements by cubic B-spline functions to solve fractional diffusion equation for force-free case formulated with Riemann-Liouville operator. Some numerical examples of interest are provided to show the accuracy of the method. A comparison between exact analytical solution and a numerical one has been made.

1. Introduction

Scientific and engineering problems including fractional derivatives have become more important in recent years. Since the description of physical and chemical processes by means of equations including fractional derivatives is more accurate and precise, their numerical solutions have been the primary interest of many recently published articles. The applications are so wide that they include such diverse areas as control theory [1], transport problems [2], tumor development [3], subdiffusive anomalous transport in the presence of an external field [4–7], and viscoelastic and viscoplastic flow [8]. These diverse areas of applications have led to an increase in the number of studies on fractional differential equations and have caused it to be an important topic in mathematics and science. Yuste [9] has used weighted average finite difference methods for fractional diffusion equations and provided some examples in which the new methods′ numerical solutions are obtained and compared against exact solutions. Langlands and Henry [10] have investigated the accuracy and stability of an implicit numerical scheme for solving the fractional diffusion equation. Murio [11] has developed an implicit unconditionally stable numerical method to solve the one-dimensional linear time fractional diffusion equation, formulated with Caputo′s fractional derivative, on a finite slab. Yuste and Acedo [12] have combined the forward time centered space (FTCS) method, well known for the numerical integration of ordinary diffusion equations, with the Grünwald-Letnikov discretization of the Riemann-Liouville derivative to obtain an FTCS scheme for solving the fractional diffusion equation.

The general form of the fractional diffusion equation for force-free case is given by [4, 13, 14]

()

where

is the fractional derivative defined by Riemann-Liouville operator as

()

where K is the diffusion coefficient and γ ∈ (0,1) is anomalous diffusion exponent. In all numerical computations, diffusion coefficient K is going to be taken as 1. In this paper, we will take the boundary conditions of (1) given in the interval 0 ≤ x ≤ 1 as

()

and the initial condition as

()

The exact analytical solution of (1) is found by the method of separation of variables [9] as

()

where E_γ is the Mittag-Leffler function [15].

In our numerical solutions, to obtain a finite element scheme for solving the fractional diffusion equation for force-free case (0 < γ ≤ 1), we will also discretize the Riemann-Liouville operator [9, 16] as

()

where

()

2. Cubic B-Spline Finite Element Collocation Solutions

To solve (1) with the boundary conditions (3) and the initial condition (4) using collocation finite element method, first of all, we define cubic B-spline base functions. Let us consider that the interval [a, b] is partitioned into N finite elements of uniformly equal length by the knots x_m, m = 0,1, 2, …, N such that a = x₀ < x₁ < ⋯<x_N = b and h = x_m+1 − x_m. The cubic B-splines ϕ_m(x), (m = −1(1)N + 1), over the interval [a, b] and at the knots x_m are defined by [17]

()

The set of cubic splines {ϕ₋₁(x), ϕ₀(x), …, ϕ_N+1(x)} constitutes a basis for the functions defined over the interval [a, b]. Thus, an approximate solution U_N(x, t) over the interval can be written in terms of the cubic B-splines trial functions as

()

where δ_m(t)′s are unknown, time dependent quantities to be determined from the boundary and cubic B-spline collocation conditions. Due to the fact that each cubic B-spline covers four consecutive elements, each element [x_m, x_m+1] is covered by four cubic B-splines. For this problem, the finite elements are identified with the interval [x_m, x_m+1] and the elements knots x_m, x_m+1. Using the nodal values U_m,

, and

given in terms of the parameter δ_m(t)

()

the variation of U_N(x, t) over the typical element [x_m, x_m+1] can now be given by

()

If we substitute the global approximation (11) and its necessary derivatives (10) into (1), we directly obtain the following set of the first-order ordinary differential equations:

()

where dot stands for derivative with respect to time. In the first place, time parameters δ_m(t) and their time derivatives

in (12) are discretized by the following Crank-Nicolson formula and first order difference formula, respectively:

()

Then, if we discretize the fractional operator

by the following formula:

()

we easily obtain a recurrence relationship between successive time levels relating unknown parameters

()

where

()

The system (15) is consisted of N + 1 linear equations including N + 3 unknown parameters (δ₋₁, …, δ_N+1) ^T. To obtain a unique solution to this system, we need two additional constraints. These are obtained from the boundary conditions and can be used to eliminate δ₋₁ and δ_N+1 from the system.

2.1. Initial State

To start iteration, we do need to evaluate the initial vector at starting time level. The initial vector

is determined from the initial and boundary conditions. Thus, the approximation (11) can be rewritten for the initial condition as

()

where the δ_m(0) are unknown element parameters. We force the initial numerical approximation U_N(x, 0) to meet the following conditions:

()

Using these conditions results in a three-diagonal system of matrix of the form

()

where

()

Solving this system yields the values of element parameters at t = 0. Now, it is time to find out the values of element parameters at different time levels using the iterative system (15).

2.2. Stability Analysis

The study of the stability of the approximation obtained by the present scheme will be based on the von Neumann stability analysis. In this analysis, the growth factor of a typical Fourier mode is defined as

()

where

. First of all, substituting the Fourier mode (21) into the recurrence relationship (15) results in the following equation:

()

Secondly, if we write

()

and assume that

()

is independent of time, then we get the following expression for the amplification factor

of the subdiffusion mode:

()

If we want the given scheme to be stable in terms of Fourier stability analysis, then the condition |ζ | ≤ 1 must be satisfied. Considering the extreme value ζ = 1, from (22) and (25), we obtain the following inequality:

()

Since α > 0, we can say that the scheme is unconditionally stable.

3. Numerical Examples and Results

Numerical results for the diffusion and diffusion-wave problems are obtained by collocation method using cubic B-spline base functions. The accuracy of the present method is measured by the error norm L₂ as

()

and the error norm L_∞ as

()

Figures 1 and 2 show the graphs of the exact (denoted by lines) solutions and the numerical ones for Δt = 0.0001 and N = 40 at t = 0.001 (denoted by triangles), t = 0.01 (denoted by squares), and t = 0.1 (denoted by stars) for two different values of γ = 0.50 and γ = 0.75, respectively. Table 1 shows the comparison of the exact solutions with the numerical ones with γ = 0.5, Δt = 0.001, and t_f = 0.1 for different values of N. The calculated error norms L₂ and L_∞ at those time levels are also presented in the table. In Table 2, the comparison of the exact solutions with the numerical ones with γ = 0.5, N = 40 and t_f = 0.1 for different values of Δt is illustrated and then the error norms L₂ and L_∞ are computed and presented in the table. In Table 3, we have listed the numerical and exact solutions of the problem for γ = 0.75, Δt = 0.001, and t_f = 0.1 for different values of N and the error norms L₂ and L_∞. Table 4 illustrates the comparison of the exact solutions with the numerical solutions for γ = 0.75, N = 40, and t_f = 0.1 for different values of Δt and the error norms L₂ and L_∞.

Table 1. The comparison of the exact solutions with the numerical solutions with γ = 0.5, Δt = 0.001, and t_f = 0.1 for different values of N and the error norms L₂ and L_∞.

x	N = 10	N = 20	N = 40	N = 80	N = 100	Exact
0.0	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
0.1	0.013806	0.013886	0.013920	0.013925	0.013926	0.013765
0.2	0.026128	0.026284	0.026325	0.026335	0.026336	0.026183
0.3	0.035777	0.035982	0.036034	0.036046	0.036048	0.036037
0.4	0.041903	0.042137	0.042195	0.042210	0.042212	0.042364
0.5	0.044001	0.044245	0.044306	0.044321	0.044323	0.044544
0.6	0.041903	0.042137	0.042195	0.042210	0.042212	0.042364
0.7	0.035777	0.035982	0.036034	0.036046	0.036048	0.036037
0.8	0.026128	0.026284	0.026325	0.026335	0.026336	0.026183
0.9	0.013806	0.013886	0.013920	0.013925	0.013926	0.013765
1.0	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000

L₂ × 10³	0.294172	0.159576	0.142246	0.139756	0.139501
L_∞ × 10³	0.543026	0.299690	0.238942	0.223758	0.221936

Table 2. The comparison of the exact solutions with the numerical solutions with γ = 0.5, N = 40, and t_f = 0.1 for different values of Δt and the error norms L₂ and L_∞.

x	Δt = 0.01	Δt = 0.001	Δt = 0.0001	Δt = 0.00001	Exact
0.0	0.000000	0.000000	0.000000	0.000000	0.000000
0.1	0.015039	0.013920	0.013929	0.013930	0.013765
0.2	0.026111	0.026325	0.026347	0.026349	0.026183
0.3	0.035392	0.036034	0.036063	0.036065	0.036037
0.4	0.041638	0.042195	0.042229	0.042233	0.042364
0.5	0.043830	0.044306	0.044341	0.044345	0.044544
0.6	0.041638	0.042195	0.042229	0.042233	0.042364
0.7	0.035392	0.036034	0.036063	0.036065	0.036037
0.8	0.026111	0.026325	0.026347	0.026349	0.026183
0.9	0.015039	0.013920	0.013929	0.013930	0.013765
1.0	0.000000	0.000000	0.000000	0.000000	0.000000

L₂ × 10³	0.836889	0.142246	0.136548	0.136264
L_∞ × 10³	1.589369	0.238942	0.203235	0.199723

Table 3. The comparison of the exact solutions with the numerical solutions with γ = 0.75, Δt = 0.001, and t_f = 0.1 for different values of N and the error norms L₂ and L_∞.

x	N = 10	N = 20	N = 40	N = 80	N = 100	Exact
0.0	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
0.1	0.018544	0.018677	0.018710	0.018718	0.018719	0.018574
0.2	0.035151	0.035393	0.035453	0.035468	0.035470	0.035331
0.3	0.048210	0.048531	0.048611	0.048631	0.048633	0.048629
0.4	0.056530	0.056900	0.056992	0.057015	0.057018	0.057166
0.5	0.048210	0.059771	0.059868	0.059892	0.059895	0.060108
0.6	0.056530	0.056900	0.056992	0.057015	0.057018	0.057166
0.7	0.048210	0.048531	0.048611	0.048631	0.048633	0.048629
0.8	0.035151	0.035393	0.035453	0.035468	0.035470	0.035331
0.9	0.018544	0.018677	0.018710	0.018718	0.018719	0.018574
1.0	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000

L₂ × 10³	0.418167	0.174101	0.136253	0.130959	0.130466
L_∞ × 10³	0.722901	0.336912	0.240523	0.216433	0.213542

Table 4. The comparison of the exact solutions with the numerical solutions with γ = 0.75, N = 40, and t_f = 0.1 for different values of Δt and the error norms L₂ and L_∞.

x	Δt = 0.01	Δt = 0.001	Δt = 0.0001	Δt = 0.00001	Exact
0.0	0.000000	0.000000	0.000000	0.000000	0.000000
0.1	0.018556	0.018710	0.018722	0.018723	0.018574
0.2	0.035089	0.035453	0.035475	0.035477	0.035331
0.3	0.048219	0.048611	0.048642	0.048644	0.048629
0.4	0.056522	0.056992	0.057028	0.057031	0.057166
0.5	0.059360	0.059868	0.059905	0.059909	0.060108
0.6	0.056522	0.056992	0.057028	0.057031	0.057166
0.7	0.048219	0.048611	0.048642	0.048644	0.048629
0.8	0.035089	0.035453	0.035475	0.035477	0.035331
0.9	0.018556	0.018710	0.018722	0.018723	0.018574
1.0	0.000000	0.000000	0.000000	0.000000	0.000000

L₂ × 10³	0.449135	0.136253	0.128451	0.127966
L_∞ × 10³	0.747758	0.240523	0.203042	0.199418

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The comparison of the exact (lines) and numerical solutions for γ = 0.50, Δt = 0.0001, and N = 40 at t = 0.001 (triangles), t = 0.01 (squares), and t = 0.1 (stars).

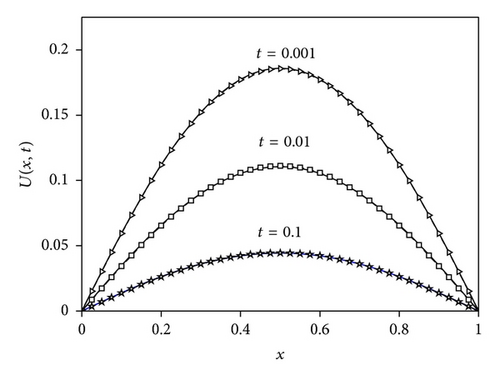
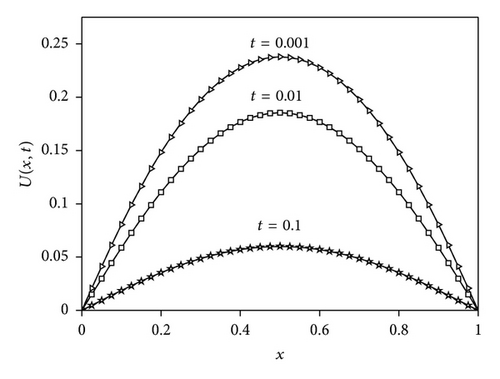
4. Conclusion

In the present study, first of all, a collocation finite element method has been constructed. Then, the method has been applied using cubic B-spline base functions. During the implementation of the method, Crank-Nicolson formula and first-order difference formula have been applied for discretization process. The stability of the method presented in the paper has been tested using the von Neumann stability analysis in which the growth factor of a typical Fourier mode is used. The accuracy of the method is also measured by the error norms L₂ and L_∞. The successful application of the present method prompts the probability of extending it to other finite element methods and other kinds of fractional differential equations. The available results suggest that this is highly probable.

References

1 R. Hilfer, Applications of Fractional Calculus in Physics, 2000, World Scientific Publishing, River Edge, NJ, USA, https://doi.org/10.1142/9789812817747, MR1890104.
10.1142/3779
Google Scholar
2 Sokolov I. M., Klafter J., and Blumen A., Fractional kinetics, Physics Today. (2002) 55, no. 11, 48–54, 2-s2.0-0036855685.
10.1063/1.1535007
CAS Web of Science® Google Scholar
3 Iomin A., Dorfman S., and Dorfman L., On tumor development: fractional transport approach, http://arxiv.org/abs/q-bio/0406001.
Google Scholar
4 Metzler R. and Klafter J., The random walk′s guide to anomalous diffusion: a fractional dynamics approach, Physics Reports. (2000) 339, no. 1, https://doi.org/10.1016/S0370-1573(00)00070-3, MR1809268, ZBL0984.82032.
10.1016/S0370-1573(00)00070-3
Web of Science® Google Scholar
5 Metzler R. and Klafter J., The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics, Journal of Physics A. (2004) 37, no. 31, R161–R208, https://doi.org/10.1088/0305-4470/37/31/R01, MR2090004, ZBL1075.82018.
10.1088/0305-4470/37/31/R01
Web of Science® Google Scholar
6 Metzler R., Barkai E., and Klafter J., Anomalous diffusion and relaxation close to thermal equilibrium: a fractional Fokker-Planck equation approach, Physical Review Letters. (1999) 82, no. 18, 3563–3567, 2-s2.0-18144408075.
10.1103/PhysRevLett.82.3563
CAS Web of Science® Google Scholar
7 Barkai E., Metzler R., and Klafter J., From continuous time random walks to the fractional Fokker-Planck equation, Physical Review E. (2000) 61, no. 1, 132–138, https://doi.org/10.1103/PhysRevE.61.132, MR1736459.
10.1103/PhysRevE.61.132
CAS Web of Science® Google Scholar
8 Diethelm K. and Freed A. D., On the solution of nonlinear fractional order differential equations used in the modelling of viscoplasticity, Scientific Computing in Chemical Engineering II:, Computational Fluid Dynamics, Reaction Engineering and Molecular Properties, 1999, Springer, Heidelberg, Germany, 217–224.
10.1007/978-3-642-60185-9_24
Google Scholar
9 Yuste S. B., Weighted average finite difference methods for fractional diffusion equations, Journal of Computational Physics. (2006) 216, no. 1, 264–274, https://doi.org/10.1016/j.jcp.2005.12.006, MR2223444, ZBL1094.65085.
10.1016/j.jcp.2005.12.006
Web of Science® Google Scholar
10 Langlands T. A. M. and Henry B. I., The accuracy and stability of an implicit solution method for the fractional diffusion equation, Journal of Computational Physics. (2005) 205, no. 2, 719–736, https://doi.org/10.1016/j.jcp.2004.11.025, MR2135000, ZBL1072.65123.
10.1016/j.jcp.2004.11.025
Web of Science® Google Scholar
11 Murio D. A., Implicit finite difference approximation for time fractional diffusion equations, Computers & Mathematics with Applications. (2008) 56, no. 4, 1138–1145, https://doi.org/10.1016/j.camwa.2008.02.015, MR2437884, ZBL1155.65372.
10.1016/j.camwa.2008.02.015
Web of Science® Google Scholar
12 Yuste S. B. and Acedo L., An explicit finite difference method and a new von Neumann-type stability analysis for fractional diffusion equations, SIAM Journal on Numerical Analysis. (2005) 42, no. 5, 1862–1874, https://doi.org/10.1137/030602666, MR2139227, ZBL1119.65379.
10.1137/030602666
Web of Science® Google Scholar
13 Balakrishman V., Anomalous diffusion in one dimension, Phsica A. (1985) 132, 569–580.
10.1016/0378-4371(85)90028-7
Web of Science® Google Scholar
14 Wyss W., The fractional diffusion equation, Journal of Mathematical Physics. (1986) 27, no. 11, 2782–2785, https://doi.org/10.1063/1.527251, MR861345, ZBL0632.35031.
10.1063/1.527251
Web of Science® Google Scholar
15 Podlubny L., Fractional Differantial Equations, 1999, Academic Press, London, UK.
Google Scholar
16 Yuste S. B. and Acedo L., An explicit finite difference method and a new von Neumann-type stability analysis for fractional diffusion equations, SIAM Journal on Numerical Analysis. (2005) 42, no. 5, 1862–1874, https://doi.org/10.1137/030602666, MR2139227, ZBL1119.65379.
10.1137/030602666
Web of Science® Google Scholar
17 Prenter P. M., Splines and Variational Methods, 1975, John Wiley & Sons, New York, NY, USA, Pure and Applied Mathematics, MR0483270.
Google Scholar

All articles

A Numerical Solution to Fractional Diffusion Equation for Force-Free Case

Abstract

1. Introduction

2. Cubic B-Spline Finite Element Collocation Solutions

2.1. Initial State

2.2. Stability Analysis

3. Numerical Examples and Results

4. Conclusion

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Numerical Solution to Fractional Diffusion Equation for Force-Free Case

Abstract

1. Introduction

2. Cubic B-Spline Finite Element Collocation Solutions

2.1. Initial State

2.2. Stability Analysis

3. Numerical Examples and Results

4. Conclusion

References

Figures

References

Related

Information