Moment Equations in Modeling a Stable Foreign Currency Exchange Market in Conditions of Uncertainty

Assumption 1. The random semi-Markov process ξ(t) can take n possible states

with transition probabilities where t₀ = 0 < t₁ < t₂ < ⋯ are the moments of time at which the jump from one state to another is realized.

If we fix any moment t > 0, then the semi-Markov process takes some of states, ξ(t) = θ_k, k = 1,2, …, n, and the state function x(t) ≡ x(t, ω) changes in accordance with the deterministic system of differential equations

So the solution of such a system is in the form

Assumption 2. The jumping time during which the process is in state θ_s before it jumps to state θ_k, s, k = 1,2, …, n is given by a discrete integer-valued random variable T_sk whose probability density function is a known function d_sk(t). Then, the intensity q_sk(t) of the jump from state θ_s to state θ_k is given by the formula

and the semi-Markov process ξ(t) is defined by the transition intensity matrix whose elements satisfy the relationships where q_k(t) is the probability density of the elapsed time T_k in state θ_k if the process jumps to it at time t_j. If ψ_k(t) denotes the probability of the event that no jump takes place during the interval (t_j, t_j+1), provided that the process jumps to the state θ_k at time t_j, then In our considerations, it will be convenient to denote the block-diagonal matrix,

Assumption 3. At the moments of jumps t_j, j = 1,2, … that are caused by some perturbations, solutions of (2) submit to the random transformations

where C_sk are m × m constant matrices and det C_sk ≠ 0.

Definition 4. Let x ∈ 𝔼_m be a continuous random variable depending on a random semi-Markov process ξ(t) with n possible states θ_k, k = 1,2, …, n. The n-dimensional column vectors E⁽¹⁾{x(t)} and n × n matrices E⁽²⁾{x(t)} of the form

where are called moments of the first or second order of the random variable x, respectively. The values $$ and $$, k = 1, …, n are called particular moments of the first or second order, respectively.

Theorem 5. Let the coefficients of the linear differential system (2) depend on a random semi-Markov process ξ(t) with transition intensity matrix (10) and, for solutions of system (2), there occur jumps (14) simultaneously with jumps of the process ξ(t). Then, the following three statements are true.

 (1) The stochastic process (x(t), ξ(t)) is defined by the operator equation

where the matrix operator $$ satisfies

 (2) The vectors of particular moments of first order satisfy

where and k = 1, …, n.

 (3) The matrix of particular moments of second order satisfies

where and k = 1, …, n.

Proof. (1)  The stochastic process (x(t), ξ(t)) is also semi-Markov because all probabilistic properties of the process for t > t_j are defined by particular probability density functions at the moment t_j of jump. Thus, there exists a linear operator L(τ) such that

Let the stochastic process ξ(t) move to state θ_k at the moment t = 0. Then, For particular density functions, when t ≥ 0, we obtain Also, with probability ψ_k(t), in view of $$, we obtain the equality On the interval (τ, τ + dτ), there could be a jump of the stochastic process ξ(τ) from state θ_k to state θ_s with probability q_ks(τ)dτ. Taking into account that functions q_ks(t) are continuous, we obtain the probability After a jump at the moment lying between moments τ and τ + dτ, we can use (27). At the moment t₁ of the first jump of the stochastic process ξ(t), in accordance with (14), we have Therefore, by using operators R, S defined in (16), to remain in state θ_k at the moment t, we get For transition from state θ_k to state θ_τ at the moment t, we obtain where τ ≠ k, τ, k = 1, …, n.

These two systems can be written in the form (22).

 (2)  Before we derive the system of moment equations in (23), we establish an auxiliary operator equation. Let us find the solution of (22) in the form

where U is an unknown matrix. If we put L(t) expressed in the form (36) into (22), we obtain After substituting r = τ + s, τ = τ in the double integral and after changing the order of integration, we obtain Therefore, a suitable matrix U in (22) is the matrix In the other way, we can find a matrix U(t) as a solution of (36) in the form where V is an unknown matrix. From this, we get A comparison of (39) and (41) implies that we can set V(t) ≡ U(t). Then, (40) can be written as or Multiplying (36) and (38) on the right by the vector f(0, x), we obtain Denote and where k = 1, …, n. The system (44) can be rewritten into the scalar form The system of (23) can be obtained by multiplying each equation of (48) by vector x and integrating it over the space 𝔼_m. In doing so, it is necessary to use

(3) The system of (25) can be obtained by multiplying each equation in (48) by matrix xx^T and integrating it over the space 𝔼_m by using matrix equalities

Definition 6. The trivial solution of system (2) is said to be mean square stable on the interval [0, ∞) if, for each ε > 0, there exists δ > 0 such that any solution x(t) corresponding to the initial data x(0) exists for all t ≥ 0 and the mathematical expectation

Definition 7. The trivial solution of system (2) is said to be asymptotically mean square stable on the interval [0, ∞) if it is stable and, moreover,

Remark 8. It is obvious that the mean stability of the zero solution of system (2) is equivalent to the asymptotic stability of the solutions of system (23) and (24) and the mean square stability of the solutions of system (2) is equivalent to the asymptotic stability of the solutions of system (25) and (26).

Definition 9. The trivial solution of the differential systems (2) is said to be L₂-stable if the integral

converges.

Remark 10. It is easy to see that the integral (53) converges if and only if the matrix integral

is convergent.

Lemma 11. The following three inequalities hold:

• (1)

  $$.

• (2)

  $$.

• (3)

  $$.

Proof. All inequalities follow from property f_k(t, x) ≥ 0, k = 1, …, n in accordance with (23) and (24).

Lemma 12. The linear matrix operators N_ks(t), k, s = 1, …, n, defined as

are monotonous.

Proof. Because q_ks(t − τ) ≥ 0, in accordance with the third statement of Lemma 11, we have

So W_s(τ) ≥ 0 implies N_ks(t)∘W_s(t) ≥ 0 and the operator is monotone.

Remark 13. The linear monotonous operator N_ks(t) transforms any symmetric matrix D into a symmetric matrix N_ks(t)∘D. Its monotonicity guarantees that inequality D₁ ≥ D₂ implies inequality

Lemma 14. The symmetric matrices W_k(t),   k = 1, …, n defined by (26) satisfy the inequalities W_k(t) ≥ 0, k = 1, …, n.

Proof. System (26) can be rewritten in the form

k = 1, …, n,    by using the matrix operators (55). System (26) as well as system (58) can be solved by the method of successive approximations Hence, $$ and $$ implies $$, k = 1, …, n. So the solution of system (58), satisfies W_k(t) ≥ 0, k = 1, …, n.

Corollary 15. Let the zero solution of the system (2) with jumps (14) at random time moments t_j, j = 0,1, 2, … determined by jumps of stochastic process ξ(t) be L₂-stable. Then, the integrals

are convergent.

Proof. This immediately follows from Lemma 14. In fact, since W_k ≥ 0, then D_k ≥ I_k, k = 1, …, n.

Theorem 16. Let the integrals (64) be convergent. Then, the zero solution of system (2) is L₂-stable if and only if the solutions W_k ≥ 0, k = 1, …, n of system (63) are bounded.

Proof. (1) Sufficiency. Integrating system (59) from 0 to ∞ with respect to t, using notation $$, k = 1, …, n, we obtain the system of matrix successive approximations

As the linear operators N_ks, k, s = 1, …, n defined by (55) are monotonous, the zero solution of system (2) is L₂-stable if the sequence of matrices $$, l = 0,1, 2, … is convergent.

(2) Necessity. Let us assume that the solution W_k = Z_k ≥ 0, k = 1, …, n of the system

is bounded. Obviously, $$, k = 1, …, n and, in view of successive approximations (65), we get So, for all l = 0,1, 2, …, we have $$, k = 1, …, n.

Next, from (65), we obtain

Moreover, because $$, $$, k = 1, …, n is satisfied for all l = 0,1, ….

Finally, the boundedness and monotonicity of the matrix sequences $$, l = 0,1, … imply the existence of limits

k = 1, …, n. Consequently, independently of the initial value $$, in view of $$, the linear operator $$ has the spectral radius less than 1. This means that system (65) has a unique solution W_k = Z_k, k = 1, …, n.

Lemma 17. If

then

Proof. Formula (20) implies $$, k = 1, …, n if t ≥ 0. Therefore, W_k(t) ≥ 0,   k = 1, …, n,   t ≥ 0. From (75), it follows that inequalities

are always satisfied. Then, for any constant $$, property (77) implies (78).

Theorem 18. Let (78) hold and let

Then, if there exist limits limits (77) exist too.

Proof. We denote

As the integrals I_k, k = 1, …, n are convergent, for all ε > 0, there exists T₁ > 0 such that, for all t > T₁, the inequalities hold. Similarly, assumption (81) means that ∀ε > 0  ∃   T₂ > 0 such that ∀t > T₂ the inequalities hold. Moreover, there exists constant W₀ such that The integral part of (75) can be now estimated if t > T₁ + T₂. We have Thus, there exist limits

Corollary 19. Let the assumptions of Theorem 18 hold. Then, the asymptotical stability of solutions of system (75) implies the asymptotical mean square stability of the zero solution of (70).

Proof. Under the given assumptions, this follows from the existence of limits (77).

Remark 20. In a particular case, solutions of (89) are located on the boundary of the stability domain. If p = 0, then Δ(0) = 0 is the equation determining the boundary of the stability domain.

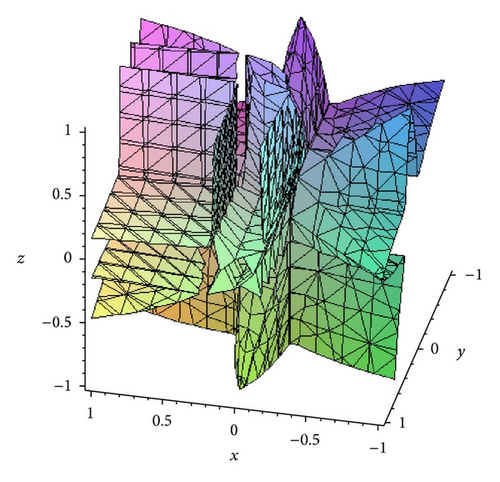
Example 21. The real boundaries of the instability domain of foreign currency exchange market can be determined in a particular case. Suppose that the random semi-Markov process can take three states:

•  

  θ₁—if the bank operates in a currency crisis, then a(ξ(t)) = a₁;

•  

  θ₂—if the bank operates in a stable foreign currency exchange market, then a(ξ(t)) = a₂;

•  

  θ₃—if the bank operates in a market with currency restrictions, then a(ξ(t)) = a₃,

with intensities which means that the bank remains in each state for the same period of time 1/T. In the above case, the system (100) takes the form where The value ρ   expresses the mean value of the bank′s income from foreign currency transactions during time T. The singular point is p = 0, when the solution is situated on the boundary of the domain of instability on the plane of coefficients a₁, a₂, and a₃.

Equation (101) is in the form

or