Volume 2013, Issue 1 160681

Research Article

Open Access

Nonlinear Fractional Jaulent-Miodek and Whitham-Broer-Kaup Equations within Sumudu Transform

Corresponding Author

Abdon Atangana

[email protected]

Institute for Groundwater Studies, Faculty of Natural and Agricultural Sciences, University of the Free State, Bloemfontein 9300, South Africa ufs.ac.za

Search for more papers by this author

Dumitru Baleanu,

Dumitru Baleanu

orcid.org/0000-0002-0286-7244

Department of Mathematics and Computer Sciences, Faculty of Art and Sciences, Cankaya University, Balgat, 06530 Ankara, Turkey cankaya.edu.tr

Department of Chemical and Materials Engineering, Faculty of Engineering, King Abdulaziz University, P.O. Box 80204, Jeddah 21589, Saudi Arabia kau.edu.sa

Institute of Space Sciences, P.O. Box MG-23, R 76900, Magurele-Bucharest, Romania spacescience.ro

Search for more papers by this author

Abdon Atangana,

Corresponding Author

Abdon Atangana

[email protected]

Institute for Groundwater Studies, Faculty of Natural and Agricultural Sciences, University of the Free State, Bloemfontein 9300, South Africa ufs.ac.za

Search for more papers by this author

Dumitru Baleanu,

Dumitru Baleanu

orcid.org/0000-0002-0286-7244

Department of Mathematics and Computer Sciences, Faculty of Art and Sciences, Cankaya University, Balgat, 06530 Ankara, Turkey cankaya.edu.tr

Department of Chemical and Materials Engineering, Faculty of Engineering, King Abdulaziz University, P.O. Box 80204, Jeddah 21589, Saudi Arabia kau.edu.sa

Institute of Space Sciences, P.O. Box MG-23, R 76900, Magurele-Bucharest, Romania spacescience.ro

Search for more papers by this author

First published: 23 May 2013

https://doi.org/10.1155/2013/160681

Citations: 24

Academic Editor: Soheil Salahshour

Share a link

Email
Wechat
Bluesky

Abstract

We solve the system of nonlinear fractional Jaulent-Miodek and Whitham-Broer-Kaup equations via the Sumudu transform homotopy method (STHPM). The method is easy to apply, accurate, and reliable.

1. Introduction

Nonlinear partial differential equations arise in various areas of physics, mathematics, and engineering [1–4]. We notice that in fluid dynamics, the nonlinear evolution equations show up in the context of shallow water waves. Some of the commonly studied equations are the Korteweg-de Vries (KdV) equation, modified KdV equation, Boussinesq equation [5], Green-Naghdi equation, Gardeners equation, and Whitham-Broer-Kaup and Jaulent-Miodek (JM) equations. Analytical solutions of these equations are usually not available. Since only limited classes of equations are solved by analytical means, numerical solution of these nonlinear partial differential equations is of practical importance. Therefore, finding new methods and techniques to deal with these type of equations is still an open problem in this area. The purpose of this paper is to find an approximated solution for the system of fractional Jaulent-Miodek and Whitham-Broer-Kaup equations (FWBK) via the Sumudu transform method. The fractional systems of partial differential equations under investigation here are given below.

The nonlinear FWBK equation which will be considered in this paper has the following form:

(1)

and the nonlinear FJM equation is

(2)

The system of (1) and (2) is subjected to the following initial conditions:

(3)

FWBK equation (1) describes the dispersive long wave in shallow water, where u(x, t) is the field of horizontal velocity, v(x, t) is the height which deviates from the equilibrium position of liquid, and α and β are constants that represent different powers. If α = 0 and β = 1, (1) reduces to the classical long-wave equations which describe the shallow water wave with diffusion [6]. If α = 1 and β = 0, (1) becomes the modified Boussinesq equations [7, 8]. FJM equation (2) appears in several areas of science such as condense matter physics [9], fluid mechanics [10], plasma physics [11], and optics [12] and associates with energy-dependent Schrödinger potential [13, 14].

The paper is organized as follows. In Section 2, we introduce briefly some of the basic tools of fractional order and of the Sumudu transform method. We show the numerical results in Section 4. The conclusions can be seen in Section 5.

2. Basic Tools

2.1. Properties and Definitions

Definition 1 (see [15]–[24].)A real function f(x), x > 0, is said to be in the space C_μ, µ ∈ ℝ if there exists a real number p > µ, such that f(x) = x^ph(x), where h(x) ∈ C[0, ∞), and it is said to be in space if f^(m) ∈ C_μ, m ∈ ℕ.

Definition 2 (see [15]–[24].)The Riemann-Liouville fractional integral operator of order α ≥ 0, of a function f ∈ C_μ, μ ≥ −1, is defined as

(4)

Properties of the operator can be found in [15–23]; we mention only the following.

For f ∈ C_μ, μ ≥ −1, α, β ≥ 0 and γ > −1

(5)

Definition 3. The Caputo fractional order derivative is given as follows [15–18]:

(6)

Definition 4. The Riemann-Liouville fractional order derivative is given as follows [16–24]:

(7)

Definition 5. The Jumarie Fractional order derivative is given as follows [24]:

(8)

Lemma 6. If m − 1 < α ≤ m, m ∈ ℕ and , μ ≥ −1, then

(9)

Definition 7 (partial derivatives of fractional order [15, 16, 19]). Assume now that f(x) is a function of n variables x_i, i = 1, …, n also of class C on D ∈ ℝ_n. As an extension of Definition 3, we define partial derivative of order α for f with respect to x_i the function

(10)

where

is the usual partial derivative of integer order m.

3. Background of Sumudu Transform

Definition 8 (see [25].)The Sumudu transform of a function f(t), defined for all real numbers t ≥ 0, is the function F_s(u), defined by

(11)

Theorem 9 (see [26].)Let G(u) be the Sumudu transform of f (t) such that

(i)
(G(1/s)/s) is a meromorphic function, with singularities having Re[s] ≤ γ;
(ii)
there exist a circular region Γ with radius R and positive constants M and K with |G(1/s)/s| < MR^−K, then the function f(t) is given by
(12)

For the proof see [26].

3.1. Basics of the Sumudu Transform Homotopy Perturbation Method

We illustrate the basic idea of this method [27–32] by considering a general fractional nonlinear nonhomogeneous partial differential equation with the initial condition of the following form:

(13)

subject to the initial condition

(14)

where

denotes without loss of generality the Caputo fraction derivative operator, f is a known function, N is the general nonlinear fractional differential operator, and L represents a linear fractional differential operator.

Applying the Sumudu transform on both sides of (10), we obtain

(15)

Using the property of the Sumudu transform, we have

(16)

Now applying the Sumudu inverse on both sides of (12) we obtain

(17)

where G(x, t) represents the term arising from the known function f(x, t) and the initial conditions.

Now we apply the following HPM:

(18)

The nonlinear term can be decomposed to

(19)

using the He’s polynomial ℋ_n(U) given as

(20)

Substituting (15) and (16) gives

(21)

which is the coupling of the Sumudu transform and the HPM using He’s polynomials. Comparing the coefficients of like powers of p, the following approximations are obtained [29, 30]:

(22)

Finally, we approximate the analytical solution U(x, t) by truncated series:

(23)

The above series solutions generally converge very rapidly [29, 30].

4. Applications

In this section, we apply this method for solving the system of the fractional differential equation. We will start with (1).

4.1. Approximate Solution of (1)

Following carefully the steps involved in the STHPM, after comparing the terms of the same power of p and choosing the appropriate initials conditions, we arrive at the following series solutions:

(24)

And so on in the same manner one can obtain the rest of the components. However, here, few terms were computed and the asymptotic solution is given by

(25)

Figures 1, 2, 3, and 4 show the graphical representation of the approximated solution of the system of nonlinear fractional Whitham-Broer-Kaup equation for η = 0.9, μ = 0.98, c₁ = c₂ = 0.1, and β = α = 0.1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Approximate solution for FWBK equation.

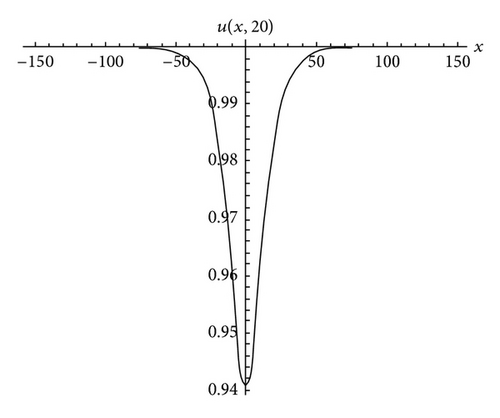
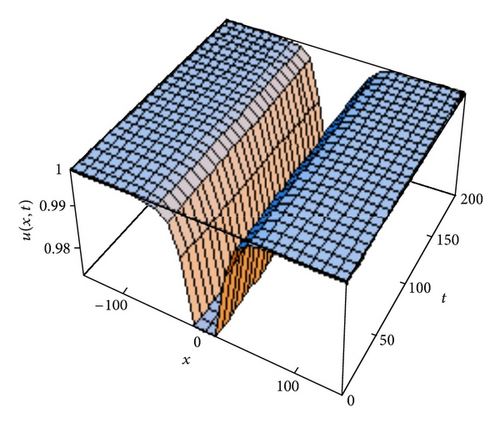
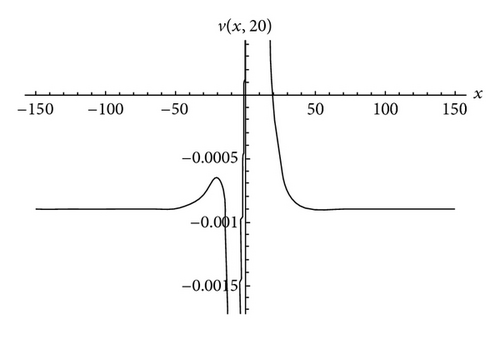
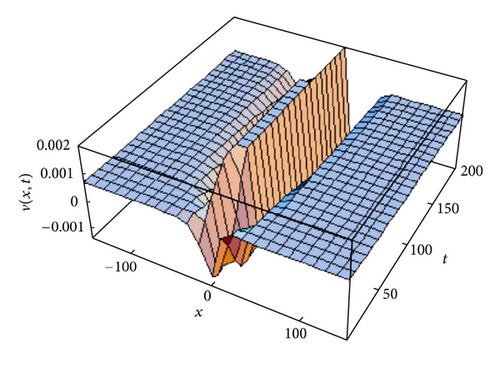
4.2. Approximate Solution of (2)

For (2), in the view of the Sumudu transform method, by choosing the appropriate initials conditions we are at the following series solutions:

(26)

And so on in the same manner one can obtain the rest of the components. However, here, few terms were computed, and the asymptotic solution of the nonlinear fractional Jaulent-Miodek is given by

(27)

Figures 5 and 6 show the graphical representation of the approximated solution of the system of nonlinear fractional Jaulent-Miodek equation for η = 0.98, μ = 0.48, and c = 0.1. Figures 5 and 6 show the approximate solution of the main problem.

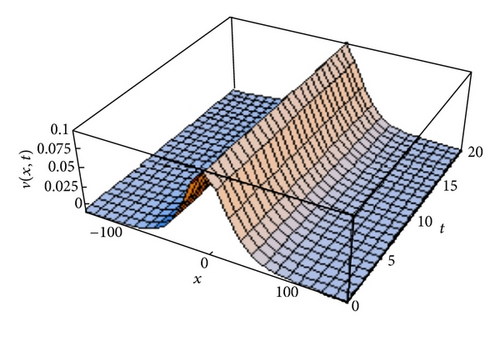
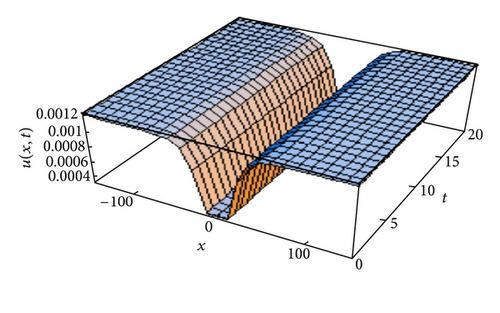
5. Conclusion

We derived approximated solutions of nonlinear fractional Jaulent-Miodek and Whitham-Broer-Kaup equations using the relatively new analytical technique the STHPM. We presented the brief history and some properties of fractional derivative concept. It is demonstrated that STHPM is a powerful and efficient tool for the system of FPDEs. In addition, the calculations involved in STHPM are very simple and straightforward.

The STHPM is chosen to solve this nonlinear problem because of the following advantages that the method has over the existing methods. This method does not require the linearization or assumptions of weak nonlinearity. The solutions are not generated in the form of general solution as in the Adomian decomposition method (ADM) [33, 34]. No correction functional or Lagrange multiplier is required in the case of the variational iteration method [35, 36]. It is more realistic compared to the method of simplifying the physical problems. If the exact solution of the partial differential equation exists, the approximated solution via the method converges to the exact solution. STHPM provides us with a convenient way to control the convergence of approximation series without adapting h, as in the case of [37] which is a fundamental qualitative difference in the analysis between STHPM and other methods. And also there is nothing like solving a partial differential equation after comparing the terms of same power of p like in the case of homotopy perturbation method (HPM) [38].

References

1 Mainardi F., Fractional calculus: some basic problems in continuum and statistical mechanics, Fractals and Fractional Calculus in Continuum Mechanics, 1997, 378, Springer, Vienna, Austria, 291–348, CISM Courses and Lectures, MR1611587, ZBL0917.73004.
10.1007/978-3-7091-2664-6_7
Google Scholar
2 Atangana A. and Alabaraoye E., Solving system of fractional partial differential equations arisen in the model of HIV infection of CD4⁺ cells and attractor one-dimensional Keller-Segel equation, Advances in Difference Equations. (2013) 2013, no. article 94, https://doi.org/10.1186/1687-1847-2013-94.
10.1186/1687-1847-2013-94
PubMed Google Scholar
3 Atangana A. and Kılıçman A., Analytical solutions of the space-time fractional derivative of advection dispersion equation, Mathematical Problems in Engineering. (2013) 2013, 9, 853127, https://doi.org/10.1155/2013/853127.
10.1155/2013/853127
Web of Science® Google Scholar
4 Atangana A. and Botha J. F., Analytical solution of the ground water flow equation obtained via homotopy decomposition method, Journal of Earth Science & Climatic Change. (2012) 3, https://doi.org/10.4172/2157-7617.1000115.
10.4172/2157-7617.1000115
Google Scholar
5 Mahmudov N. I., Approximate controllability of fractional sobolev-type evolution equations in banach spaces, Abstract and Applied Analysis. (2013) 2013, 9, 502839, https://doi.org/10.1155/2013/502839.
10.1155/2013/502839
Google Scholar
6 Mohebbi A. and Asgari Z., Efficient numerical algorithms for the solution of “good” Boussinesq equation in water wave propagation, Computer Physics Communications. (2011) 182, no. 12, 2464–2470, https://doi.org/10.1016/j.cpc.2011.07.004, MR2838403.
10.1016/j.cpc.2011.07.004
CAS Web of Science® Google Scholar
7 Xie F., Yan Z., and Zhang H., Explicit and exact traveling wave solutions of Whitham-Broer-Kaup shallow water equations, Physics Letters A. (2001) 285, no. 1-2, 76–80, https://doi.org/10.1016/S0375-9601(01)00333-4, MR1842720, ZBL0969.76517.
10.1016/S0375-9601(01)00333-4
CAS Web of Science® Google Scholar
8 Kupershmidt B. A., Mathematics of dispersive water waves, Communications in Mathematical Physics. (1985) 99, no. 1, 51–73, MR791640, https://doi.org/10.1007/BF01466593, ZBL1093.37511.
10.1007/BF01466593
Web of Science® Google Scholar
9 Ma W.-X., Li C.-X., and He J., A second Wronskian formulation of the Boussinesq equation, Nonlinear Analysis. Theory, Methods & Applications. (2009) 70, no. 12, 4245–4258, https://doi.org/10.1016/j.na.2008.09.010, MR2514756, ZBL1159.37425.
10.1016/j.na.2008.09.010
Web of Science® Google Scholar
10 Hong T., Wang Y. Z., and Huo Y. S., Bogoliubov quasiparticles carried by dark solitonic excitations in non-uniform Bose-Einstein condensates, Chinese Physics Letters. (1998) 15, 550–552.
10.1088/0256-307X/15/8/002
CAS Web of Science® Google Scholar
11 Zhang J.-f., Multiple soliton solutions of the dispersive long-wave equations, Chinese Physics Letters. (1999) 16, no. 1, 4–5, https://doi.org/10.1088/0256-307X/16/1/002, MR1712070.
10.1088/0256-307X/16/1/002
Web of Science® Google Scholar
12 Das G. C., Sarma J., and Uberoi C., Explosion of a soliton in a multicomponent plasma, Physics of Plasmas. (1997) 4, no. 6, 2095–2100, https://doi.org/10.1063/1.872545, MR1450558.
10.1063/1.872545
CAS Web of Science® Google Scholar
13 Lou S. Y., A direct perturbation method: nonlinear Schrodinger equation with loss, Chinese Physics Letters. (1999) 16, 659–661, https://doi.org/10.1088/0256-307X/16/9/014.
10.1088/0256-307X/16/9/014
Web of Science® Google Scholar
14 Atangana A. and Cloot A. H., Stability and convergence of the space fractional variable-order Schrödinger equation, Advances in Difference Equations. (2013) 2013, no. article 80, https://doi.org/10.1186/1687-1847-2013-80, MR3047859.
10.1186/1687-1847-2013-80
PubMed Google Scholar
15 Baleanu D., Diethelm K., Scalas E., and Trujillo J. J., Fractional Calculus Models and Numerical Methods, 2012, 3, World Scientific, Hackensack, NJ, USA, Series on Complexity, Nonlinearity and Chaos, https://doi.org/10.1142/9789814355216, MR2894576, ZBL1258.35201.
10.1142/8180
Google Scholar
16 Kilbas A. A., Srivastava H. M., and Trujillo J. J., Theory and Applications of Fractional Differential Equations, 2006, 204, Elsevier Science B. V., Amsterdam, The Netherlands, North-Holland Mathematics Studies, MR2218073, https://doi.org/10.1016/S0304-0208(06)80001-0, ZBL1206.26007.
10.1016/S0304-0208(06)80001-0
Google Scholar
17 Oldham K. B. and Spanier J., The Fractional Calculus, Mathematics in Science and Engineering, 1974, 111, Academic Press, New York, NY, USA, MR0361633, ZBL0292.26011.
Google Scholar
18 B. Ross, Fractional Calculus and Its Applications, 1975, 457, Springer, Berlin, Germany, Lecture Notes in Mathematics, MR0367127.
10.1007/BFb0067095
Google Scholar
19 Luchko Y. and Gorenflo R., The initial value problem for some fractional differential equations with the Caputo derivative, Preprint Series, 1998, no. A08-98, Fachbreich Mathematik and Informatik, Freic Universitat Berlin.
Google Scholar
20 Atangana A. and Secer A., A note on fractional order derivatives and table of fractional derivatives of some special functions, Abstract and Applied Analysis. (2013) 2013, 8, 279681.
10.1155/2013/279681
Google Scholar
21 Podlubny I., Fractional Differential Equations, 1999, 198, Academic Press, San Diego, Calif, USA, Mathematics in Science and Engineering, MR1658022, ZBL1056.93542.
Web of Science® Google Scholar
22 Samko S. G., Kilbas A. A., and Marichev O. I., Fractional Integrals and Derivatives: Theory and Applications, 1993, Gordon and Breach Science, Yverdon, Switzerland, MR1347689, ZBL0924.44003.
Google Scholar
23 Miller K. S. and Ross B., An Introduction to the Fractional Calculus and Fractional Differential Equations, 1993, John Wiley & Sons, New York, NY, USA, A Wiley-Interscience, MR1219954, ZBL0943.82582.
Google Scholar
24 Jumarie G., On the representation of fractional Brownian motion as an integral with respect to (dt) ^a, Applied Mathematics Letters. (2005) 18, no. 7, 739–748, https://doi.org/10.1016/j.aml.2004.05.014, MR2144721, ZBL1082.60029.
10.1016/j.aml.2004.05.014
Web of Science® Google Scholar
25 Watugala G. K., Sumudu transform: a new integral transform to solve differential equations and control engineering problems, International Journal of Mathematical Education in Science and Technology. (1993) 24, no. 1, 35–43, https://doi.org/10.1080/0020739930240105, MR1206847, ZBL0768.44003.
10.1080/0020739930240105
Google Scholar
26 Weerakoon S., Application of Sumudu transform to partial differential equations, International Journal of Mathematical Education in Science and Technology. (1994) 25, no. 2, 277–283, https://doi.org/10.1080/0020739940250214, MR1271656, ZBL0812.35004.
10.1080/0020739940250214
Google Scholar
27 Singh J., Kumar D., and Kılıçman A., Homotopy perturbation method for fractional gas dynamics equation using Sumudu transform, Abstract and Applied Analysis. (2013) 2013, 8, 934060, https://doi.org/10.1155/2013/934060.
10.1155/2013/934060
Google Scholar
28 Eltayeb H. and Kılıçman A., A note on the Sumudu transforms and differential equations, Applied Mathematical Sciences. (2010) 4, no. 21-24, 1089–1098, MR2607362, ZBL1207.34014.
Google Scholar
29 Kılıçman A., Eltayeb H., and Agarwal P. R., On Sumudu transform and system of differ ential equations, Abstract and Applied Analysis. (2010) 2010, 11, 598702, https://doi.org/10.1155/2010/598702.
10.1155/2010/598702
Google Scholar
30 Gupta V. G. and Sharma B., Application of Sumudu transform in reaction-diffusion systems and nonlinear waves, Applied Mathematical Sciences. (2010) 4, no. 9–12, 435–446, MR2580638, ZBL1195.26012.
Google Scholar
31 Eltayeb H. and Kılıçman A., A note on the Sumudu transforms and differential equations, Applied Mathematical Sciences. (2010) 4, no. 21–24, 1089–1098, MR2607362, ZBL1207.34014.
Google Scholar
32 Belgacem F. B. M., Karaballi A. A., and Kalla S. L., Analytical investigations of the Sumudu transform and applications to integral production equations, Mathematical Problems in Engineering. (2003) no. 3-4, 103–118, https://doi.org/10.1155/S1024123X03207018, MR2032184.
10.1155/S1024123X03207018
Web of Science® Google Scholar
33 Abdon A., New cass of boundary value problems, Informations Sciences Letters. (2012) 1, no. 2, 67–76.
10.12785/isl/010201
Google Scholar
34 Wu G.-C., Adomian decomposition method for non-smooth initial value problems, Mathematical and Computer Modelling. (2011) 54, no. 9-10, 2104–2108, https://doi.org/10.1016/j.mcm.2011.05.018, MR2834614, ZBL1235.65105.
10.1016/j.mcm.2011.05.018
Google Scholar
35 Wu G. C. and Baleanu D., Variational iteration method for the Burgers′ flow with fractional derivatives-New Lagrange multipliers, Applied Mathematical Modelling. (2012) 5, 1012–1018.
Google Scholar
36 Wu G.-C. and Baleanu D., Variational iteration method for fractional calculus—a universal approach by Laplace transform, Advances in Difference Equations. (2013) 2013, no. article 18, https://doi.org/10.1186/1687-1847-2013-18, MR3020186.
10.1186/1687-1847-2013-18
PubMed Google Scholar
37 Xu H., Liao S.-J., and You X.-C., Analysis of nonlinear fractional partial differential equations with the homotopy analysis method, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 4, 1152–1156, https://doi.org/10.1016/j.cnsns.2008.04.008, MR2468947, ZBL1221.65286.
10.1016/j.cnsns.2008.04.008
Web of Science® Google Scholar
38 He J.-H., Homotopy perturbation method with an auxiliary term, Abstract and Applied Analysis. (2012) 2012, 7, 857612, https://doi.org/10.1155/2012/857612, MR2879936, ZBL1235.65096.
10.1155/2012/857612
Google Scholar

Citing Literature

All articles

Nonlinear Fractional Jaulent-Miodek and Whitham-Broer-Kaup Equations within Sumudu Transform

Abstract

1. Introduction