Volume 2013, Issue 1 152518

Research Article

Open Access

The Twisting Bifurcations of Double Homoclinic Loops with Resonant Eigenvalues

Xiaodong Li,

Xiaodong Li

School of Mathematics and Statistics, Northeast Normal University, Changchun, Jilin 130024, China nenu.edu.cn

Search for more papers by this author

Weipeng Zhang,

Corresponding Author

Weipeng Zhang

[email protected]

School of Mathematics and Statistics, Northeast Normal University, Changchun, Jilin 130024, China nenu.edu.cn

Search for more papers by this author

Fengjie Geng,

Fengjie Geng

School of Information Engineering, China University of Geosciences (Beijing), Beijing 100083, China cugb.edu.cn

Search for more papers by this author

Jicai Huang,

Jicai Huang

School of Mathematics and Statistics, Central China Normal University, Wuhan, Hubei 430079, China ccnu.edu.cn

Search for more papers by this author

Xiaodong Li,

Xiaodong Li

School of Mathematics and Statistics, Northeast Normal University, Changchun, Jilin 130024, China nenu.edu.cn

Search for more papers by this author

Weipeng Zhang,

Corresponding Author

Weipeng Zhang

[email protected]

School of Mathematics and Statistics, Northeast Normal University, Changchun, Jilin 130024, China nenu.edu.cn

Search for more papers by this author

Fengjie Geng,

Fengjie Geng

School of Information Engineering, China University of Geosciences (Beijing), Beijing 100083, China cugb.edu.cn

Search for more papers by this author

Jicai Huang,

Jicai Huang

School of Mathematics and Statistics, Central China Normal University, Wuhan, Hubei 430079, China ccnu.edu.cn

Search for more papers by this author

First published: 20 May 2013

https://doi.org/10.1155/2013/152518

Academic Editor: Maoan Han

Share a link

Email
Wechat
Bluesky

Abstract

The twisting bifurcations of double homoclinic loops with resonant eigenvalues are investigated in four-dimensional systems. The coexistence or noncoexistence of large 1-homoclinic orbit and large 1-periodic orbit near double homoclinic loops is given. The existence or nonexistence of saddle-node bifurcation surfaces is obtained. Finally, the complete bifurcation diagrams and bifurcation curves are also given under different cases. Moreover, the methods adopted in this paper can be extended to a higher dimensional system.

1. Introduction and Setting of the Problem

In recent years, there is a large literature concerning the bifurcation problems of homoclinic and heteroclinic loops in dynamical systems (see [1–23] and the references therein). However, to the best of the authors’ knowledge, less attention has been devoted to the bifurcation of double homoclinic loops. Han and Bi [24] investigated the existence of homoclinic bifurcation curves and small and large limit cycles bifurcated from a double homoclinic loop under multiple parameter perturbations for general planar systems. Han and Chen [25] gave the number of limit cycles near double homoclinic loops under perturbations in planar Hamiltonian systems. Homburg and Knobloch [26] considered the existence of two homoclinic orbits in the bellows configuration, where the homoclinic orbits approach the equilibrium along the same direction for positive and negative times in conservative and reversible systems. Morales et al. [27, 28] presented contracting and expanding Lorenz attractors through resonant double homoclinic loops. Lu [29] obtained codimension 2 bifurcations of twisted double homoclinic loops in higher dimensional systems. Ragazzo [30] investigated the stability of sets that were generalizations of the simple pendulum double homoclinic loop. In our recent work [31, 32], codimension 2 bifurcations of double homoclinic loops and codimension 3 bifurcations of nontwisted double homoclinic loops with resonant eigenvalues were studied. Concerning this topic, a more extensive list of references can be found in the references mentioned earlier. Generally speaking, when studying the problem of single homoclinic or heteroclinic bifurcation connecting hyperbolic equilibrium, the bifurcation is more complicated as Γ is twisted. Moreover, it is known that double homoclinic loops have higher codimension than a single homoclinic loop under the same conditions. Therefore, it will be more challenging and difficult to analyze the twisting bifurcations of double homoclinic loops.

In this paper, on the one hand, using the method which was originally established in [22, 23] and then improved in [9, 17, 21], and so forth, we study the bifurcations of double homoclinic loops with resonant eigenvalues under twisted cases. Besides, the method is more applicable and bifurcation equations obtained in this paper are easier to compute. On the other hand, frequently, the too many equivalent terms in the bifurcation equation will make the bifurcation equation more complex so that it is very difficult to analyze the bifurcation equation. Applying the method used by Homburg and Knobloch [26] to analyze the center-stable and center-unstable tangent bundles, we cannot only get a smooth coordinate transformation in the neighborhood of Γ small enough, but also make the bifurcation equation definite under an additional condition. Such strategy in dealing with the problems of bifurcations from homoclinic and heteroclinic loops is rarely used in the existing literatures. Therefore, a main feature in this paper is a combination of geometrical and analytical methods.

Motivated by these points, we will consider the following C^r system and its unperturbed system:

()

where r is large enough, z ∈ R⁴, μ ∈ R^l, l ≥ 3, 0<|μ | ≪ 1, f(0) = 0, g(0, μ) = g(z, 0) = 0.

We make the following assumptions, which are shown in Figure 1.

H₁ The linearization Df(0) has simple real eigenvalues at the equilibrium 0 : −ρ₂, −ρ₁, λ₁, λ₂ satisfying
()
H₂ System (2) has double homoclinic loops Γ = Γ₁ ∪ Γ₂, Γ_i = {z = r_i(t) : t ∈ R, r_i(±∞) = 0} and , i = 1,2, where W^s and W^u are the stable and unstable manifolds of 0, respectively.
H₃ Let , and , unit eigenvectors corresponding to λ₁ and −ρ₁, respectively, and satisfying , .
H₄ as t ≫ 1, and as t ≪ −1, i = 1,2.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Double homoclinic loops Γ = Γ₁ ∪ Γ₂.

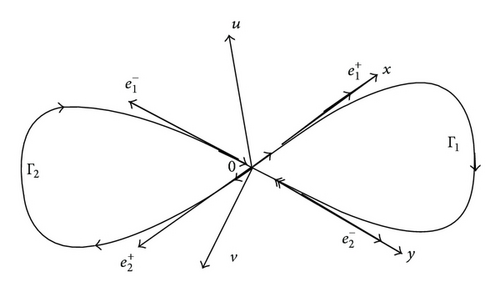
As shown in Figure 1, under the hypotheses (H₁)–(H₄), we can see that the double homoclinic loops Γ are of codimension 3.

The single homoclinic loop in high-dimensional systems has been investigated by many authors (see [1, 2, 4–8, 13–15, 17, 21, 22] and the references therein). In this paper, we only focus on bifurcations of the large loop; that is, the double loops Γ = Γ₁ ∪ Γ₂.

A nondegenerate homoclinic orbit is called a nontwisted homoclinic orbit if the unstable manifold W^u has an even number of half-twists along the homoclinic orbit, and is called a twisted homoclinic orbit if W^u has an odd number of half-twists along the homoclinic orbit; see more details in Deng [4]. A characterization for a twisted homoclinic orbit is that it arises from and tends to the equilibrium point from different sides of the unstable manifold. However, a nontwisted homoclinic orbit does so from the same side of the manifold. For the double homoclinic loop, Γ = Γ₁ ∪ Γ₂, it is called double twisted if both Γ₁ and Γ₂ are twisted, single twisted if and only if one of them is twisted, and nontwisted otherwise.

The rest of this paper is organized as follows. In Section 2, the normal form in a neighborhood of the equilibrium small enough is established and the bifurcation equations are given. In Section 3, by bifurcation analysis, the results of twisting bifurcations and complete bifurcation diagrams are obtained under different cases. We end the paper with a conclusion in Section 4.

2. Normal Form and Bifurcation Equations

From the hypothesis (H₁), we can see that we confine ourselves to consider the resonance taking place between the two principal eigenvalues λ₁ and −ρ₁. Moreover, the corresponding eigenvectors are also the tangent directions of the homoclinic orbits. For simplicity, we may choose a new parameter μ = (α, ν) such that ρ₁(μ) = λ₁(ν) + αλ₁(ν), −1 ≪ α ≪ 1.

Let U be a neighborhood of 0 small enough. By analyzing the center-stable and center-unstable tangent bundles, Homburg and Knobloch [26] obtained that there is a smooth coordinate transformation, such that in U system (1) takes the following form:

()

For the definiteness of the bifurcation equation, we make an additional assumption as follows:

(H₅) H₁(x, 0,0) = 0, H₂(0, y, 0) = 0; that is,
()

where k_i > λ₂/λ₁, i = 1,3, 5, k₂ρ₁/λ₁ > 2, k₄ρ₂/λ₁ > 2, (k₆ρ₁ + k₇ρ₂)/λ₁ > 2. l_i > ρ₂/ρ₁, i = 1,3, 5, l₂λ₁/ρ₁ > 2, l₄λ₂/ρ₁ > 2, (l₆λ₁ + l₇λ₂)/ρ₁ > 2.

By the same process as in [32], which is based on the analysis of the Poincaré return map defined on some local transversal section of the double homoclinic loop Γ, we obtain the bifurcation equations as follows:

()

3. Bifurcation Analysis

Denote that . We say that Γ is nontwisted as Δ₁ = Δ₂ = 1 and twisted as Δ₁ = Δ₂ = −1 or Δ₁Δ₂ = −1. In this paper, we focus on the twisted bifurcations. It is easy to see that is the approximate expanding rate of the solution from to .

Case 1 (Δ1 = Δ2 = − 1 (i.e., double twisted)). For convenience and simplicity, we use the following notations throughout Case 1:

()

If (6) has solution s₁ = s₂ = 0, then we have

()

, then there exists a codimension 1 surface Σ_i with a normal vector

at ν = 0, such that the ith equation of (6) has solution s₁ = s₂ = 0 as ν ∈ Σ_i and |ν | ≪ 1; that is, Γ_i is persistent. If rank

, then Σ₁₂ = Σ₁∩Σ₂ is a codimension 2 surface with a normal plane span

such that (6) has solution s₁ = s₂ = 0 as ν ∈ Σ₁₂ and |ν | ≪ 1; equivalently, the large loop Γ = Γ₁ ∪ Γ₂ is persistent.

Suppose that (6) has solution s₁ = 0, s₂ > 0. Then, we have

()

Hence, we obtain the large 1-homoclinic orbit bifurcation surface equation

()

which is well defined at least in the region

and has a normal vector

as α > 0 (resp.,

as α < 0) at ν = 0 such that system (1) has a large 1-homoclinic loop

near Γ as

. It also means that

is tangent to Σ₂ as α > 0 (resp., Σ₁ as α < 0). When

, α > 0, s₁ = 0, and

., (6) indicates that

()

Using (11)

(12), we have

()

So, s₁ = s₁(ν) increases along the direction of the gradient

for ν near

Similarly, by setting , we can derive that s₁(ν) increases along the direction for ν near as α < 0.

If (6) has solution s₁ > 0 and s₂ = 0, then we have

()

Therefore, we obtain the existence of the other large 1-homoclinic orbit bifurcation surface equation

()

which is well defined at least in the region

and has a normal vector

as α > 0 (resp.,

as α < 0) at ν = 0 such that system (1) has a large 1-homoclinic loop

near Γ as

. Thus,

is also tangent to Σ₁ as α > 0 (resp., Σ₂ as α < 0). For

and α > 0,

., s₂ = 0, it follows from (6) that

()

Computing (17)

(16), it leads to

()

So, s₂ = s₂(ν) increases along the direction

for ν close to

By a similar procedure, we can show that s₂(ν) increases along the direction as ν is in the neighborhood of and α < 0.

Summing up the previous analysis, we have the following theorem.

Theorem 1. Suppose that (H₁)–(H₅) hold; then, the following conclusions are true.

(1)
If , then there exists a unique surface Σ_i with codimension 1 and normal vectors at ν = 0, such that system (1) has a homoclinic loop near Γ_i if and only if ν ∈ Σ_i and |ν | ≪ 1. If , then Σ₁₂ = Σ₁∩Σ₂ is a codimension 2 surface and 0 ∈ Σ₁₂ such that system (1) has a large loop consisting of two homoclinic orbits near Γ as ν ∈ Σ₁₂ and |ν | ≪ 1; that is, Γ is persistent.
(2)
In the region , there exists a large 1-homoclinic orbit bifurcation surface which is tangent to Σ₂ (resp., Σ₁) at ν = 0 with the normal vector (resp., ) as α > 0 (resp., α < 0), and for , system (1) has a unique large 1-homoclinic orbit near Γ. Furthermore, the unique large 1-homoclinic orbit near Γ becomes a large 1-periodic orbit when ν moves along the direction (resp., ) and nearby as α > 0 (resp., α < 0). Meanwhile, there exists another large 1-homoclinic orbit bifurcation surface which is tangent to Σ₁ (resp., Σ₂) at ν = 0 with the normal (resp., ) as α > 0 (resp., α < 0), and for , system (1) has another one unique large 1-homoclinic orbit near Γ. Furthermore, the unique large 1-homoclinic orbit near Γ changes into a large 1-periodic orbit when ν shifts along the direction (resp., ) and near as α > 0 (resp., α < 0).

Lemma 2. Suppose that hypotheses (H₁)–(H₅) and 0 < α ≪ 1 are valid; then, in addition to the large 1-homoclinic loop , system (1) has exactly one simple large 1-periodic orbit near Γ for . Moreover, the large 1-periodic orbit is persistent as ν changes in the neighborhood of .

Proof. If and |ν | ≪ 1, then we know that system (1) has one large 1-homoclinic loop . Now, following (6), we have

()

Let N₁(s₁) and L₁(s₁) be the left- and right-hand sides of (19), respectively. Then, by (10), we get N₁(0) = L₁(0) as

. Moreover,

()

Thus,

. Therefore, there is an

, such that for

, N₁(s₁) > L₁(s₁).

Let . Then,

()

which means that

. Then, it follows from

that N₁(s₁) = L₁(s₁) has a unique solution

satisfying

, which is shown in Figure 2. That is, system (1) has a unique large 1-periodic loop near Γ for

and 0<|ν | ≪ 1. The proof is complete.

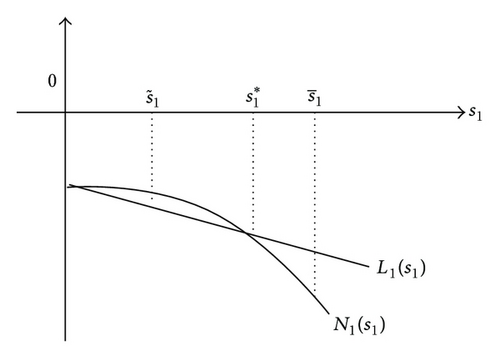
Lemma 3. Suppose that hypotheses (H₁)–(H₅) and 0 < α ≪ 1 hold. Then, system (1) has a saddle-node bifurcation surface of large 1-periodic orbit in the region as follows:

()

Proof. It is easy to see that h = N₁(s₁) is tangent to h = L₁(s₁) at some point s₁, as shown in Figure 3; if

()

then

()

It is not difficult to see that (24) and (25) have a unique small positive solution

()

when

and

. Substituting (26) into (24), we get the surface SN². It is easy to verify that the solution s₂ of (6) is positive as s₁ is given by (26) and ν ∈ SN². Thus, the proof of the lemma is complete.

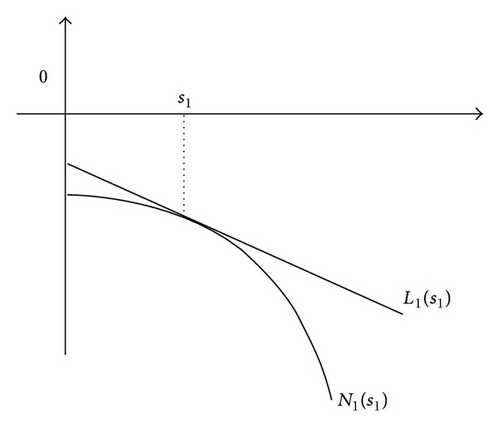
Remark 4. Due to , we see that the line L₁(s₁) lies above the curve N₁(s₁) as ν ∈ SN². Moreover, . decreases as and ν moves along the direction ; in this case, system (1) exhibits two large 1-periodic orbits. And as ν leaves SN² along the opposite direction, there is no large 1-periodic orbit.

Corollary 5. The bifurcation surface {0 < α ≪ 1} × SN² and the region have no intersection point.

Proof. Let , where 0 < a < δ⁻¹e² is a given constant; then, in view of and (1 + α) ^1/α → e as α → 0, we know the right side of the expression SN² as follows:

()

and

is the left side of the expression SN². Hence, the proof is complete.

Corollary 6. As , the bifurcation surface {0 < α ≪ 1} × SN² and the region have no intersection point.

Proof. Still let , where 0 < a < δ⁻¹e² is a given constant; then, due to , we know that

()

, a > 0 is a constant, and α > 0 is small enough, it is easy to see that R > L. This contradicts the expression of SN². The proof is complete.

By a similar analysis as in Lemmas 2 and 3, we can obtain the following results.

Lemma 7. Suppose that hypotheses (H₁)–(H₅) and 0 < α ≪ 1 are valid; then, in addition to the large 1-homoclinic loop , system (1) has exactly one simple large 1-periodic orbit near Γ for . Moreover, the large 1-periodic orbit is persistent as ν changes in the neighborhood of .

Lemma 8. Suppose that hypotheses (H₁)–(H₅) and 0 < α ≪ 1 hold. Then, system (1) has a saddle-node bifurcation surface of large 1-periodic orbit in the region as follows:

()

Remark 9. Let and . Due to and ., we claim that the line L₂(s₂) lies above the curve N₂(s₂) as ν ∈ SN¹, and when and ν leaves SN¹ along the direction , L₂(0) decreases; hence, system (1) has two large 1-periodic orbits, and when ν moves along the direction , there is no large 1-periodic orbit.

Corollary 10. The bifurcation surface {0 < α ≪ 1} × SN¹ and the region have no intersection point.

Corollary 11. As , the bifurcation surface {0 < α ≪ 1} × SN¹ and the region have no intersection point.

In the following we define open regions in the neighborhood of the origin of the ν-space, which are shown in Figures 4 and 5.

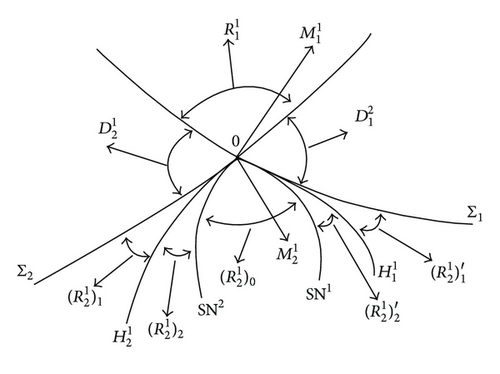
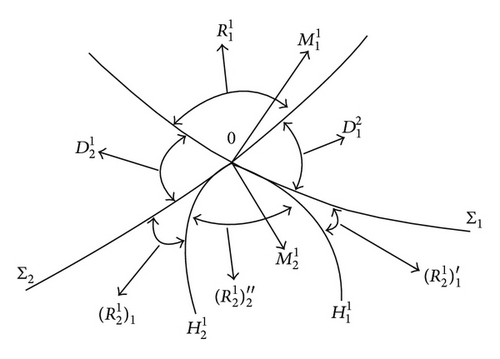
is bounded by SN¹ and SN², is bounded by Σ₂ and , is bounded by and SN², is bounded by SN¹ and SN², is bounded by SN¹ and , is bounded by Σ₁ and Σ₂, and is bounded by and .

Now, the previous analysis is summarized in the following three theorems, as shown in Figures 4 and 5.

Theorem 12. Suppose that hypotheses (H₁)–(H₅) hold, 0 < α ≪ 1, , , and . Then, system (1)

(1)
has exactly one simple large 1-periodic orbit near Γ as ;
(2)
has a unique double large 1-periodic orbit near Γ as ν ∈ SN²;
(3)
has exactly two simple large 1-periodic orbits near Γ as ;
(4)
has exactly one simple large 1-periodic orbit and one large 1-homoclinic loop near Γ as ;
(5)
does not have any large 1-periodic and large 1-homoclinic loop near Γ as ;
(6)
has exactly one simple large 1-periodic orbit near Γ as ;
(7)
has a unique double large 1-periodic orbit near Γ as ν ∈ SN¹;
(8)
has exactly two simple large 1-periodic orbits near Γ as ;
(9)
has exactly one simple large 1-periodic orbit and one large 1-homoclinic loop near Γ as .

Theorem 13. Suppose that hypotheses (H₁)–(H₅) hold, 0 < α ≪ 1, , , and . Then system (1)

(1)
has exactly one simple large 1-periodic orbit near Γ as ;
(2)
has exactly one simple large 1-periodic orbit and one large 1-homoclinic loop near Γ as ;
(3)
has exactly two simple large 1-periodic orbits near Γ as ;
(4)
has exactly one simple large 1-periodic orbit and one large 1-homoclinic loop near Γ as ;
(5)
has exactly one simple large 1-periodic orbit near Γ as .

Remark 14. Suppose that hypotheses (H₁)–(H₅) hold, 0 < α ≪ 1, , ; then the conclusions of Theorem 13 are still true, and the bifurcation diagram is the same as Figure 5.

Denote by the open region with boundaries Σ₁ and Σ₂, such that . is the open region with boundaries Σ₂ and Σ₁, such that .

From the bifurcation equations (6), we have the following theorem.

Theorem 15. Suppose that hypotheses (H₁)–(H₅) hold, and 0 < α ≪ 1. Then, system (1)

(1)
does not have any large 1-periodic orbit near Γ as ;
(2)
does not have any large 1-periodic orbit near Γ as ;
(3)
does not have any large 1-periodic orbit near Γ as .

Remark 16. For −1 ≪ α < 0, by the same analysis, we can obtain the analogous results as those in Theorems 12–15. In fact, in the case we can reverse the time t and change (x, y, u, v) to (y, x, v, u), and then we still get 0 < α ≪ 1.

At last, we consider the case α = 0. By a similar process to that of Section 3, we obtain the bifurcation equations

()

For the same reason as before, we have the following theorem.

Theorem 17. Suppose that (H₁)–(H₅), α = 0, and hold; then,

(1)
as , system (1) not only has a large 1-homoclinic orbit bifurcation surface
()
with a normal vector at ν = 0, but also has another large 1-homoclinic orbit bifurcation surface
()
with a normal vector at ν = 0,
(2)
as either , , and or , , and , system (1) has a unique large 1-periodic orbit near Γ.

Case 2 (Δ1 = −1, Δ2 = 1 (i.e., single twisted)). Similar to Case 1, for convenience and simplicity, we use the following notations:

()

If (6) has a solution s₁ = s₂ = 0, then we have

()

, then there exists a codimension 1 surface

with a normal vector

at ν = 0, such that the ith equation of (6) has solution s₁ = s₂ = 0 as

and |ν | ≪ 1; that is, Γ_i is persistent. If rank

, then

is a codimension 2 surface with a normal plane span

such that (6) has solution s₁ = s₂ = 0 as

and |ν | ≪ 1; equivalently, the large loop Γ = Γ₁ ∪ Γ₂ is persistent.

Suppose that (6) has solution s₁ = 0, s₂ > 0. Then, we have

()

Hence, we get the large 1-homoclinic orbit bifurcation surface equation

()

which is well defined at least in the region

and has a normal vector

as α > 0 (resp.,

as α < 0) at ν = 0 such that the system (1) has a large 1-homoclinic loop

near Γ as

. It also means that

is tangent to

as α > 0 (resp.,

as α < 0). When

, α > 0, s₁ = 0, and

., (6) implies that

()

Using (37)

(38), we get

()

So, s₁ = s₁(ν) increases along the direction of the gradient

for ν near

Similarly, by setting , we can derive that s₁(ν) increases along the direction for near as α > 0.

If (6) has solution s₁ > 0 and s₂ = 0, then we get

()

Therefore, we obtain the existence of the other large 1-homoclinic orbit bifurcation surface equation

()

which is well defined at least in the region

and has a normal vector

as α > 0 (resp.,

as α < 0) at ν = 0 such that the system (1) has a large 1-homoclinic loop

near Γ as

. Thus,

is also tangent to

as α > 0 (resp.,

as α < 0). For

and α > 0,

., s₂ = 0, it follows from (6) that

()

Computing (43)

(42), it leads to

()

So, s₂ = s₂(ν) increases along the direction

for ν close to

By a similar procedure, we can show that s₂(ν) increases along the direction as ν is in the neighborhood of and α < 0.

Summarizing the previous analysis, we have the following theorem.

Theorem 18. Suppose that (H₁)–(H₅) hold; then, the following conclusions are true.

(1)
If , then there exists a unique surface with codimension 1 and normal vectors at ν = 0, such that system (1) has a homoclinic loop near Γ_i if and only if and |ν | ≪ 1. If , then is a codimension 2 surface and such that system (1) has a large loop consisting of two homoclinic orbits near Γ as and |ν | ≪ 1; that is, Γ is persistent.
(2)
In the region , there exists a unique large 1-homoclinic orbit bifurcation surface which is tangent to (resp., ) at ν = 0 with the normal vector (resp., ) as α > 0 (resp., α < 0), and for , system (1) has a unique large 1-homoclinic orbit near Γ. Furthermore, the unique large 1-homoclinic orbit near Γ becomes a large 1-periodic orbit when ν moves along the direction (resp., ) and nearby as α > 0 (resp., α < 0). In the region , there exists another unique large 1-homoclinic orbit bifurcation surface which is tangent to (resp., ) at ν = 0 with the normal (resp., ) as α > 0 (resp., α < 0), and for , system (1) has another one unique large 1-homoclinic orbit near Γ. Furthermore, the unique large 1-homoclinic orbit near Γ changes into a large 1-periodic orbit when ν shifts along the direction (resp., ) and nearby as α > 0 (resp., α < 0).

Lemma 19. Suppose that hypotheses (H₁)–(H₅) and 0 < α ≪ 1 are valid; system (1) has only a unique large 1-homoclinic orbit near Γ for and 0<|ν | ≪ 1.

Proof. If and |ν | ≪ 1, from Theorem 18, we know that system (1) has one large 1-homoclinic loop . Now, following (6), we have

()

Let N₁(s₁) and L₁(s₁) be the left- and right-hand sides of (45), respectively. Then, by (36), we get N₁(0) = L₁(0) as

. Moreover,

()

Thus,

, and

. Therefore, N₁(s₁) < L₁(s₁) for s₁ ≠ 0, as shown in Figure 6.

Therefore, system (1) has only a unique large 1-homoclinic orbit near Γ for and 0<|ν | ≪ 1.

Remark 20. Due to , we can see that the line N₁(s₁) lies under the curve L₁(s₁) as . Moreover, . decreases as and ν moves along the direction ; in this case, system (1) has a unique large 1-periodic orbit. And as ν leaves along the opposite direction, there is no large 1-periodic orbit.

By a similar analysis as in Lemma 19, we can obtain the following results.

Lemma 21. Suppose that hypotheses (H₁)–(H₅) and 0 < α ≪ 1 are valid; system (1) has only a unique large 1-homoclinic orbit near Γ for and 0<|ν | ≪ 1.

Remark 22. Let and . Due to and ., we claim that the line L₂(s₂) lies under the curve N₂(s₂) as , and when and ν leaves along the direction , L₂(0) increases; hence, system (1) has a unique large 1-periodic orbit, and when ν moves along the direction , there is no large 1-periodic orbit.

In the following we define open regions in the neighborhood of the origin of the ν-space, which are shown in Figure 7.

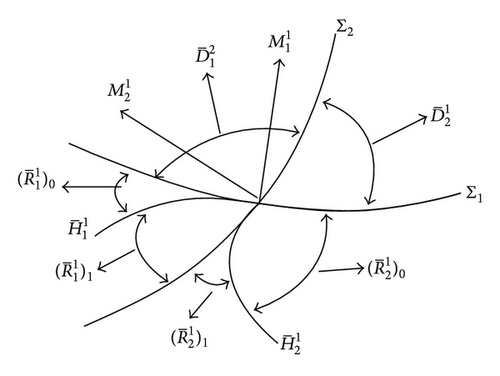
is bounded by Σ₁ and , is bounded by Σ₂ and , is bounded by and Σ₂, is bounded by Σ₁ and , is bounded by Σ₁ and Σ₂, and is bounded by Σ₂ and Σ₁.

From the previous analysis, we obtain the following three theorems, as shown in Figure 7.

Theorem 23. Suppose that hypotheses (H₁)–(H₅) hold, 0 < α ≪ 1, . Then, system (1)

(1)
does not have any large 1-periodic orbit and large 1-homoclinic loop near Γ as ;
(2)
has a unique large 1-homoclinic loop near Γ as ;
(3)
has a unique large 1-periodic orbit near Γ as .

Theorem 24. Suppose that hypotheses (H₁)–(H₅) hold, 0 < α ≪ 1, . Then, system (1)

(1)
has no large 1-periodic orbit and large 1-homoclinic loop near Γ as ;
(2)
has a unique large 1-homoclinic loop near Γ as ;
(3)
has a unique large 1-periodic orbit near Γ as .

From the bifurcation equations, we have the following theorem easily.

Theorem 25. Suppose that hypotheses (H₁)–(H₅) hold, and 0 < α ≪ 1. Then, system (1)

(1)
has no large 1-periodic orbit near Γ as ;
(2)
has no large 1-periodic orbit near Γ as .

Remark 26. For −1 ≪ α < 0, by the same analysis, we can obtain the analogous results as those in Theorems 23–25. In fact, in the case we can reverse the time t and change (x, y, u, v) to (y, x, v, u), and then we still get 0 < α ≪ 1.

At last, we consider the case α = 0. By a similar process to that of Section 3, we obtain the bifurcation equations

()

For the same reason as before, we have the following theorem.

Theorem 27. Suppose that (H₁)–(H₅), α = 0, and hold; then,

(1)
as , system (1) has a unique large 1-homoclinic orbit bifurcation surface
()
with a normal vector at ν = 0;
(2)
as , system (1) also has a unique large 1-homoclinic orbit bifurcation surface
()
with a normal vector at ν = 0;
(3)
as and , system (1) has a unique large 1-periodic orbit near Γ.

Remark 28. As Γ₁ is nontwisted and Γ₂ is twisted, we can obtain similar conclusions as shown in Case 2.

4. Conclusion

This paper is devoted to investigating the twisting bifurcations of double homoclinic loops with resonant eigenvalues in 4-dimensional systems. We give asymptotic expressions of the bifurcation surfaces and their relative positions, describe the existence regions of large 1-periodic orbits near Γ in Lemmas 2 and 7, and obtain the sufficient conditions for the existence or nonexistence of saddle-node bifurcation surfaces in Lemmas 3 and 8. More importantly, the complete bifurcation diagrams are given under different cases in Figures 4, 5, and 7. According to our analysis, when Γ is double twisted, in Theorems 12–15, we obtain one bifurcation diagram with saddle-node bifurcation surfaces of large 1-periodic orbit when and the other bifurcation diagram without saddle-node bifurcation surfaces when . When Γ is single twisted, in Theorems 23–25, we obtain another bifurcation diagram. Compared with the nontwisted cases in Zhang et al. [32], our paper shows completely different results and bifurcation diagrams. It is worthy to be mentioned that the restriction on the dimension is not essential, the method used in this paper can be extended to higher dimensional systems without any difficulty, and the same conclusions can be deduced under the same hypotheses. Furthermore, we mention some problems for future study. (1) W^s or W^u is inclination flip on one of the double homoclinic loops. (2) Both W^s and W^u are inclination flips on the double homoclinic loops and so on. But the difficulty of these problems will increase with adding codimension of the double homoclinic loops.

Acknowledgments

The research was supported by National Natural Science Foundation of China (nos. 11001041, 11101170, 11202192, 11271065 and 10926105), SRFDP (no. 200802001008), and the State Scholarship Fund of the China Scholarship Council (nos. 2011662521, and 2011842509).

References

1 Blázquez-Sanz D. and Yagasaki K., Analytic and algebraic conditions for bifurcations of homoclinic orbits I: saddle equilibria, Journal of Differential Equations. (2012) 253, no. 11, 2916–2950, https://doi.org/10.1016/j.jde.2012.08.008, MR2968187.
10.1016/j.jde.2012.08.008
Web of Science® Google Scholar
2 Chow S.-N., Deng B., and Fiedler B., Homoclinic bifurcation at resonant eigenvalues, Journal of Dynamics and Differential Equations. (1990) 2, no. 2, 177–244, https://doi.org/10.1007/BF01057418, MR1050642, ZBL0703.34050.
10.1007/BF01057418
Google Scholar
3 Chow S.-N. and Lin X.-B., Bifurcation of a homoclinic orbit with a saddle-node equilibrium, Differential and Integral Equations. (1990) 3, no. 3, 435–466, MR1047746, ZBL0727.58026.
10.57262/die/1371571144
Google Scholar
4 Deng B., Homoclinic twisting bifurcations and cusp horseshoe maps, Journal of Dynamics and Differential Equations. (1993) 5, no. 3, 417–467, https://doi.org/10.1007/BF01053531, MR1235038, ZBL0782.34042.
10.1007/BF01053531
Google Scholar
5 Gruendler J., Homoclinic solutions for autonomous dynamical systems in arbitrary dimension, SIAM Journal on Mathematical Analysis. (1992) 23, no. 3, 702–721, https://doi.org/10.1137/0523036, MR1158829, ZBL0767.34028.
10.1137/0523036
Web of Science® Google Scholar
6 Gruendler J., Homoclinic solutions for autonomous ordinary differential equations with nonautonomous perturbations, Journal of Differential Equations. (1995) 122, no. 1, 1–26, https://doi.org/10.1006/jdeq.1995.1136, MR1356127, ZBL0840.34045.
10.1006/jdeq.1995.1136
Web of Science® Google Scholar
7 Homburg A. J., Global aspects of homoclinic bifurcations of vector fields, Memoirs of the American Mathematical Society. (1996) 121, no. 578, MR1327210, ZBL0862.34042.
10.1090/memo/0578
Web of Science® Google Scholar
8 Homburg A. J. and Krauskopf B., Resonant homoclinic flip bifurcations, Journal of Dynamics and Differential Equations. (2000) 12, no. 4, 807–850, https://doi.org/10.1023/A:1009046621861, MR1826963, ZBL0990.37038.
10.1023/A:1009046621861
Google Scholar
9 Jin Y. L. and Zhu D. M., Bifurcations of rough heteroclinic loop with two saddle points, Science in China A. (2003) 46, no. 4, 459–468, https://doi.org/10.1360/03ys9047, MR2014478, ZBL1215.37039.
10.1360/03ys9047
Google Scholar
10 Kisaka M., Kokubu H., and Oka H., Bifurcations to n-homoclinic orbits and n-periodic orbits in vector fields, Journal of Dynamics and Differential Equations. (1993) 5, no. 2, 305–357, https://doi.org/10.1007/BF01053164, MR1223451.
10.1007/BF01053164
Google Scholar
11 Kokubu H., Komuro M., and Oka H., Multiple homoclinic bifurcations from orbit-flip. I. Successive homoclinic doublings, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (1996) 6, no. 5, 833–850, https://doi.org/10.1142/S0218127496000461, MR1404121, ZBL0884.34047.
10.1142/S0218127496000461
Web of Science® Google Scholar
12 Knobloch J. and Wagenknecht T., Homoclinic snaking near a heteroclinic cycle in reversible systems, Physica D. (2005) 206, no. 1-2, 82–93, https://doi.org/10.1016/j.physd.2005.04.018, MR2166527, ZBL1084.34049.
10.1016/j.physd.2005.04.018
Web of Science® Google Scholar
13 Liu X. and Zhu D., Bifurcation of degenerate homoclinic orbits to saddle-center in reversible systems, Chinese Annals of Mathematics. Series B. (2008) 29, no. 6, 575–584, https://doi.org/10.1007/s11401-008-0038-5, MR2470615, ZBL1197.34067.
10.1007/s11401-008-0038-5
Web of Science® Google Scholar
14 Oldeman B. E., Krauskopf B., and Champneys A. R., Numerical unfoldings of codimension-three resonant homoclinic flip bifurcations, Nonlinearity. (2001) 14, no. 3, 597–621, https://doi.org/10.1088/0951-7715/14/3/309, MR1830909, ZBL0990.37039.
10.1088/0951-7715/14/3/309
Web of Science® Google Scholar
15 Sandstede B., Constructing dynamical systems having homoclinic bifurcation points of codimension two, Journal of Dynamics and Differential Equations. (1997) 9, no. 2, 269–288, https://doi.org/10.1007/BF02219223, MR1451292, ZBL0879.34051.
10.1007/BF02219223
Google Scholar
16 Schecter S. and Sourdis C., Heteroclinic orbits in slow-fast Hamiltonian systems with slow manifold bifurcations, Journal of Dynamics and Differential Equations. (2010) 22, no. 4, 629–655, https://doi.org/10.1007/s10884-010-9171-4, MR2734473, ZBL1213.34072.
10.1007/s10884-010-9171-4
Web of Science® Google Scholar
17 Shui S. L. and Zhu D. M., Codimension 3 nonresonant bifurcations of homoclinic orbits with two inclination flips, Science in China A. (2005) 48, no. 2, 248–260, https://doi.org/10.1360/03ys0201, MR2158603, ZBL1170.37325.
10.1360/03ys0201
Google Scholar
18 Wagenknecht T., Two-heteroclinic orbits emerging in the reversible homoclinic pitchfork bifurcation, Nonlinearity. (2005) 18, no. 2, 527–542, https://doi.org/10.1088/0951-7715/18/2/004, MR2122672, ZBL1067.37023.
10.1088/0951-7715/18/2/004
Web of Science® Google Scholar
19 Wiggins S., Global Bifurcations and Chaos, 1988, 73, Springer, New York, NY, USA, https://doi.org/10.1007/978-1-4612-1042-9, MR956468.
10.1007/978-1-4612-1042-9
Google Scholar
20 Wiggins S., Introduction to Applied Nonlinear Dynamical Systems and Chaos, 1990, 2, Springer, New York, NY, USA, MR1056699.
10.1007/978-1-4757-4067-7
Google Scholar
21 Zhang T. and Zhu D., Codimension 3 homoclinic bifurcation of orbit flip with resonant eigenvalues corresponding to the tangent directions, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2004) 14, no. 12, 4161–4175, https://doi.org/10.1142/S0218127404011880, MR2118644, ZBL1072.37041.
10.1142/S0218127404011880
Web of Science® Google Scholar
22 Zhu D. M., Problems in homoclinic bifurcation with higher dimensions, Acta Mathematica Sinica. (1998) 14, no. 3, 341–352, https://doi.org/10.1007/BF02580437, MR1693164, ZBL0932.37032.
10.1007/BF02580437
Google Scholar
23 Zhu D. and Xia Z., Bifurcations of heteroclinic loops, Science in China A. (1998) 41, no. 8, 837–848, https://doi.org/10.1007/BF02871667, MR1667063, ZBL0993.34040.
10.1007/BF02871667
Google Scholar
24 Han M. and Bi P., Bifurcation of limit cycles from a double homoclinic loop with a rough saddle, Chinese Annals of Mathematics B. (2004) 25, no. 2, 233–242, https://doi.org/10.1142/S025295990400024X, MR2055274, ZBL1059.34027.
10.1142/S025295990400024X
Web of Science® Google Scholar
25 Han M. A. and Chen J., On the number of limit cycles in double homoclinic bifurcations, Science in China A. (2000) 43, no. 9, 914–928, https://doi.org/10.1007/BF02879797, MR1804043, ZBL1013.34026.
10.1007/BF02879797
Google Scholar
26 Homburg A. J. and Knobloch J., Multiple homoclinic orbits in conservative and reversible systems, Transactions of the American Mathematical Society. (2006) 358, no. 4, 1715–1740, https://doi.org/10.1090/S0002-9947-05-03793-1, MR2186994, ZBL1162.34034.
10.1090/S0002-9947-05-03793-1
Web of Science® Google Scholar
27 Morales C. A., Pacifico M. J., and San Martin B., Expanding Lorenz attractors through resonant double homoclinic loops, SIAM Journal on Mathematical Analysis. (2005) 36, no. 6, 1836–1861, https://doi.org/10.1137/S0036141002415785, MR2178223, ZBL1093.37022.
10.1137/S0036141002415785
Web of Science® Google Scholar
28 Morales C. A., Pacifico M. J., and San Martin B., Contracting Lorenz attractors through resonant double homoclinic loops, SIAM Journal on Mathematical Analysis. (2006) 38, no. 1, 309–332, https://doi.org/10.1137/S0036141004443907, MR2217319, ZBL1107.37041.
10.1137/S0036141004443907
Web of Science® Google Scholar
29 Lu Q., Codimension 2 bifurcation of twisted double homoclinic loops, Computers & Mathematics with Applications. (2009) 57, no. 7, 1127–1141, https://doi.org/10.1016/j.camwa.2008.11.015, MR2508543, ZBL1186.34054.
10.1016/j.camwa.2008.11.015
Web of Science® Google Scholar
30 Ragazzo C. G., On the stability of double homoclinic loops, Communications in Mathematical Physics. (1997) 184, no. 2, 251–272, https://doi.org/10.1007/s002200050060, MR1462746, ZBL0876.70011.
10.1007/s002200050060
Web of Science® Google Scholar
31 Zhang W. P. and Zhu D. M., Codimension 2 bifurcations of double homoclinic loops, Chaos, Solitons and Fractals. (2009) 39, no. 1, 295–303, https://doi.org/10.1016/j.chaos.2007.01.101, MR2504567, ZBL1197.37065.
10.1016/j.chaos.2007.01.101
Web of Science® Google Scholar
32 Zhang W., Zhu D., and Liu D., Codimension 3 nontwisted double homoclinic loops bifurcations with resonant eigenvalues, Journal of Dynamics and Differential Equations. (2008) 20, no. 4, 893–908, https://doi.org/10.1007/s10884-008-9105-6, MR2448217, ZBL1195.34058.
10.1007/s10884-008-9105-6
Web of Science® Google Scholar

All articles

The Twisting Bifurcations of Double Homoclinic Loops with Resonant Eigenvalues

Abstract

1. Introduction and Setting of the Problem

2. Normal Form and Bifurcation Equations

3. Bifurcation Analysis

4. Conclusion

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Twisting Bifurcations of Double Homoclinic Loops with Resonant Eigenvalues

Abstract

1. Introduction and Setting of the Problem

2. Normal Form and Bifurcation Equations

3. Bifurcation Analysis

4. Conclusion

Acknowledgments

References

Figures

References

Related

Information