We consider the effect of time delay and cross diffusion on the dynamics of a modified Leslie-Gower predator-prey model incorporating a prey refuge. Based on the stability analysis, we demonstrate that delayed feedback may generate Hopf and Turing instability under some conditions, resulting in spatial patterns. One of the most interesting findings is that the model exhibits complex pattern replication: the model dynamics exhibits a delay and diffusion controlled formation growth not only to spots, stripes, and holes, but also to spiral pattern self-replication. The results indicate that time delay and cross diffusion play important roles in pattern formation.

1. Introduction

The spatial component of ecological interaction has been identified as an important factor in how ecological communities are shaped. Understanding the role of space is challenging both theoretics and empirism [1]. Empirical evidence suggests that the spatial scale and structure of environment can influence population interactions [2]. And pattern formation in nonlinear complex systems is one of the central problems of the natural, social, and technological sciences [3–12]. The classical approach to the origin of spatial structures was developed by Turing [13]. Understanding of patterns and mechanisms of species spatial dispersal is an issue of significant current interest in conservation biology and ecology. It arises from many ecological applications; particularly, it plays a major role in connection to biological invasion and disease spreading [14, 15].

In recent years, one of the important predator-prey models is Leslie-Gower model. A modified version of reaction-diffusion Leslie-Gower predator-prey model with Holling-type II functional response takes the form [16, 17]

()

where u and v are prey and predator densities, respectively. r, a, d, b_i, and c_i (i = 1,2) are positive constants. r is the growth rate of preys, d is the growth rate of predators, a is the strength of competition among individuals of species u, b₁ (resp., b₂) measures the extent to which environment provides protection to prey u (resp., to the predator v), and c₁ is the maximum value of the per capita reduction of u due to v. c₂ has a similar meaning to c₁. d₁ and d₂ are the diffusion coefficients that imply the movement of individuals from a higher to a lower concentration region. ∇² = (∂²/∂x²)+(∂²/∂y²) is the usual Laplacian operator in two-dimensional space.

For model (1), Camara and Aziz-Alaoui [18–20] paid more attention to pattern formation in the spatial domain and observed the labyrinth, chaos, and spiral wave patterns. In addition, Guan et al. [21] studied model (1) incorporating a refuge protecting mu of the prey in the case of c₁ = c₂ ≠ 0 and b₁ = b₂ ≠ 0, where m ∈ [0,1) is a constant. This leaves (1 − m)u of the prey available to the predator, and model (1) becomes

()

In [21], the authors proved the global stability of the positive equilibria, determined the Turing space in the spatial domain, and performed a series of numerical simulations and found that model (2) exhibits complex Turing pattern replication: spots, stripes, and holes patterns.

On the other hand, a time delay occurs naturally in just about every interaction of the real world. The original motivations for studying delay differential equations mainly come from their applications in feedback control theory [22–29]. And time delay also is an ubiquitous phenomenon in biological systems and has an important role in affecting population dynamics. In a system described by ordinary differential equations, time delay could change qualitatively the nature of the equilibrium from a stable equilibrium to an unstable one and thus induces bifurcation [30]. For a predator-prey system, time delay was often realized as feedback. The effect of this kind of delay on the dynamical behavior of populations has been studied by a number of papers [31–33]. Because of the importance of time delay to control dynamics of a system, a number of works have been done on effect of delay on the spatial-temporal system [34–44]. In our previous work [43], we studied the spatiotemporal complexity of a Leslie-Gower model incorporating a prey refuge with time delay effect:

()

where τ > 0 is a constant delay due to gestation and u(x, y, t − τ) and v(x, y, t − τ) are densities of prey and predator, respectively, at moment t − τ and position (x, y). For simplicity, set u(x, y, t − τ)∶ = u(t − τ), v(x, y, t − τ)∶ = v(t − τ). In [43], we analyzed the effects of delay and diffusion on the spatiotemporal dynamics of model (3) and gave the pattern formation via numerical simulation.

Furthermore, in nature, there is a tendency that the preys would keep away from predators and the escape velocity of the preys may be taken as proportional to the dispersive velocity of the predators [45–49]. In the same manner, there is a tendency that the predators would get closer to the preys and the chase velocity of predators may be considered to be proportional to the dispersive velocity of the preys. Keeping these in view, cross-diffusion arises, which was proposed first by Kerner [50] and first applied in competitive population system by Shigesada et al. [51]. And there comes a question: how does cross-diffusion affect pattern formation in a delayed Leslie-Gower predator-prey model incorporating a prey refuge?

In this paper, we mainly focus on the effect of cross-diffusion on the pattern formation in the following Leslie-Gower predator-prey model incorporating a prey refuge:

()

where the cross-diffusion coefficients d₁₂ and d₂₁ express the respective population fluxes of the preys and predators resulting from the presence of the other species, respectively. Other parameters are the same definitions as model (3). And we call

()

the diffusive matrix and assume that d₁₁ > 0, d₂₂ > 0, and det (D) = d₁₁d₂₂ − d₁₂d₂₁ > 0.

Following [44], we explain the meaning and units of each variable and constant in model (4).

(i)
The prey u and predator v are usually measured in mg of dry weight per liter [mg·dw/l].
(ii)
Time t and time delay τ are measured in days [d].
(iii)
The length of x, y ∈ (0, L) is measured in meter [m].
(iv)
r is the growth rate of prey u and d is the growth rate of predator v, measured in [d⁻¹].
(v)
c is the maximum value of the per capita reduction of v due to u, which is not available in abundance and is measured in [d⁻¹].
(vi)
a describes the strength of competition among individuals of species u and is measured in [(mg · dw/l) ⁻¹d⁻¹].
(vii)
b describes the extent to which environment provides protection to prey u and predator v and is usually measured in mg of dry weight per liter [mg·dw/l].
(viii)
d_ij > 0 (i, j = 1,2) are the diffusion coefficients corresponding to the prey and predator, respectively, and are measured in [m²d⁻¹].

Model (4) is to be analyzed under the following nonzero initial conditions:

()

and zero-flux boundary conditions:

()

In the above, L denotes the size of the system in square domain, and n is the outward unit normal vector of the boundary ∂Ω. The main reason for choosing such boundary conditions is that we are interested in the self-organization of pattern, and zero-flux conditions imply no external input [5].

This paper is organized as follows. In the next section, we mainly present the Hopf and Turing bifurcation analysis. In Section 3, we perform a series of numerical simulation to show evolution process of prey u. And in the last section, we give some concluding remarks.

2. Bifurcation Analysis

In this section, we will focus on the conditions of Hopf and Turing bifurcation. Following [40, 43], if time delay τ is small, one can expand u (x, y, t − τ) and v (x, y, t − τ) as

()

Substituting (8) into (4), we obtain

()

Expanding (9) in Taylor series and neglecting the higher-order nonlinearities, then (9) becomes

()

where h_u(u, v) = (∂h(u, v)/∂u) and h_v(u, v) = (∂h(u, v)/∂v).

From (10), we finally obtain that

()

Equation (11) can be used to analyze the bifurcation of model (4) when τ is small.

It is easy to obtain that model (11) has three boundary equilibria E₁ = (0,0), E₂ = ((a/r), 0), and E₃ = (0, (bd/r)) and a unique positive equilibrium E^* = (u^*, v^*) = (((dm − d + cr)/ac), (((cab + (dm − d + cr)(1 − m))d)/ac²)).

Remark 1. In the case without time delay and cross-diffusion, that is, τ = 0 and d₁₂ = d₂₁ = 0, model (11) becomes (2). It is easy to see that E₁, E₂, E₃, and E^* are also equilibria of model (2). The stabilities of these equilibria of model (2) can be seen in [21].

In the following, we are mainly concerned with the properties of Hopf and Turing bifurcations for model (11).

Let 0 = μ₀ < μ₁ < μ₂ < ⋯ be the eigenvalues of the operator −Δ on Ω with the zero-flux boundary conditions. And setting

()

{ϕ_ij∣j = 1, …, dim E(μ_i)} will be an orthonormal basis of E(μ_i), and X_ij = {cϕ_ij∣c ∈ ℝ²}; then

, where

The linearization of model (11) around E^* = (u^*, v^*) can be expressed by

()

with domain X. Here,

()

with

, and

. Since τ is small, we only consider this case of τ < (1/d) (i.e. 𝒳 > 0) in this paper.

For each j (j = 0,1, 2, …), X_j is invariant under the operator , and λ is an eigenvalue of D∇² + L_E on X_j if and only if λ is an eigenvalue of the matrix for some j ≥ 0.

So the stability is reduced to consider the characteristic equation

()

where

()

2.1. Hopf Bifurcation

In this subsection, we analyze the properties of Hopf bifurcation for model (11). For Hopf bifurcation to occur at the positive equilibrium E^*, the matrix

must have an eigenvalues on the imaginary axis [52]; that is, trace (M_j) ≡ 0. Therefore, the only possible critical values of τ are τ(i) such that, for i ≥ 0,

()

At τ = τ(i),

, and therefore, if i ≥ 1, for all 0 ≤ j < i, trace (M_i) > 0 and the matrix

has at least 2i eigenvalues with positive real parts. Therefore, the only value of τ at which Hopf bifurcation hypotheses may be satisfied is

()

Near τ_c, the complex conjugate pair κ(τ) ± iω(τ) is given by

()

Since κ(τ_c) = 0 and

, there exists an interval I containing τ_c such that

(i)
ω²(τ) ≠ 0 for all τ ∈ I;
(ii)
trace (M_j) < 0 and det (M_j) > 0 with uniformly for j ≥ 1 and τ ∈ I;
(iii)
.

Thus, we have the following theorem.

Theorem 2. If , then model (11) undergoes a Hopf bifurcation that occurs around the positive equilibrium E^* at τ = τ_c.

2.2. Turing Instability

In this subsection, we will state the Turing instability for the positive equilibrium E^* of model (11).

Mathematically speaking, the positive equilibrium E^* is Turing instability, which was emphasized by Turing in his pioneering work in 1952 [13], which means that it is asymptotically stable in the absence of diffusion in model (11) but unstable with respect to solutions in model (11). Hence, Turing instability occurs when either the condition trace (M_j) < 0 or the condition det (M_j) > 0 is violated.

Since the positive equilibrium E^* is stable without diffusion which means that

and

hold, then trace (M_j) < 0 is always true. Therefore, for the emergency of the diffusion-driven instability in model (11), it is needed that det (M_j) < 0 for some μ_j > 0. A necessary condition is

()

otherwise det (M_j) > 0 for all j > 0 since 𝒳det (D) > 0 and

. And we notice that det (M_j) achieves its minimum:

()

at the critical value

where

()

Summarizing the above calculation, we conclude the following.

Theorem 3. If

()

then the positive equilibrium E^* of model (11) is Turing unstable.

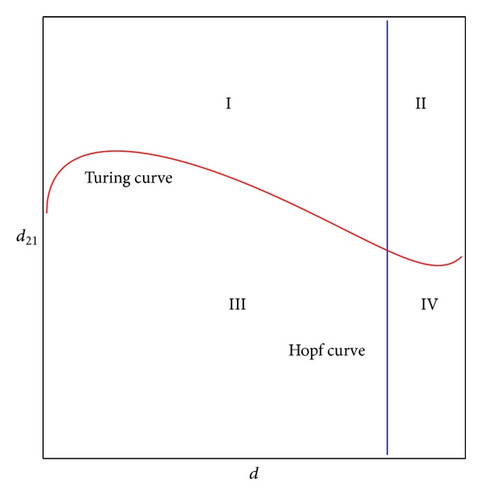
In Figure 1, we show the bifurcation diagram for model (11). The Turing instability curve and Hopf bifurcation curve separate the d − d₂₁ parameter space into four domains. The domain on the left of the Hopf bifurcation curve is stable; the domain above Turing bifurcation curve is unstable. Hence, among these domains, only the domain I satisfies conditions of Theorem 3, and we call domain I as Turing space, where the Turing instability occurs and the Turing patterns may be undergone. Domain IV gives birth to spiral patterns.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Bifurcation diagram for model (11) in the d − d₂₁ parameter space. The red line is Turing bifurcation curve, and the blue line denotes Hopf bifurcation. Domain I is the region of pure Turing instability. In domain II, Hopf-Turing instability occurs. And domain III is the stable region. Domain IV is the region of pure Hopf instability.

3. Pattern Formation via Numerical Simulations

In this section, we perform extensive numerical simulations of the spatially extended model (4) in two-dimension spaces, and the qualitative results are shown here. Our numerical simulations employ a system size of 100 × 100 space units. And some parameters are taken as

()

The numerical integration of model (4) was performed by means of forward Euler integration, with a time step of Δt = 0.001 and a space step of Δx = Δy = (1/4), using the standard five-point approximation for the 2D Laplacian with the zero-flux boundary conditions [53].

3.1. Turing Pattern Formation in Domain I

In this subsection, we first consider the pattern formation when parameters are located in domain I of Figure 1, which is pure Turing unstable domain.

Initially, the entire system is placed in the steady state (u^*, v^*), and the propagation velocity of the initial perturbation is thus on the order of 5 × 10⁻⁴ space units per time unit. The initial data of prey u is a 101 × 101 matrix, such as

()

where rand (101,101) is MATLAB procedure, which returns a 101 × 101 matrix containing pseudorandom values drawn from the standard uniform distribution on the open interval (0,1). And the system is then integrated for 2,000,000 time steps, and the last images are saved. After the initial period during which the perturbation spreads, the system goes into an essentially steady state (time independent).

In the numerical simulations, different types of dynamics are observed, and it is found that the distributions of predator and prey are always of the same type. Consequently, we can restrict our analysis of pattern formation to one distribution. In the following, we show the distribution of prey u.

In Figure 2, we show three typical Turing patterns and their three-dimension pattern for model (4) at t = 2000. In the case of (d, d₂₁, d₂₂) = (0.08,0.89,0.37), the equilibrium is (u^*, v^*) = (2.8697,0.5203) and the holes patterns are isolated zones with low prey density (cf. Figure 2(a)). When increasing d to 0.4, (d, d₂₁, d₂₂) = (0.47,0.89,0.37), (u^*, v^*) = (0.9877,1.2218), the stripes patterns appear. While with (d, d₂₁, d₂₂) = (0.61,0.39,0.75), (u^*, v^*) = (0.3122,0.7306), spots patterns are isolated zones with high prey density (cf. Figure 2(c)). And Figures 2(d)-2(e) are three-dimension patterns corresponding to Figures 2(a)–2(c).

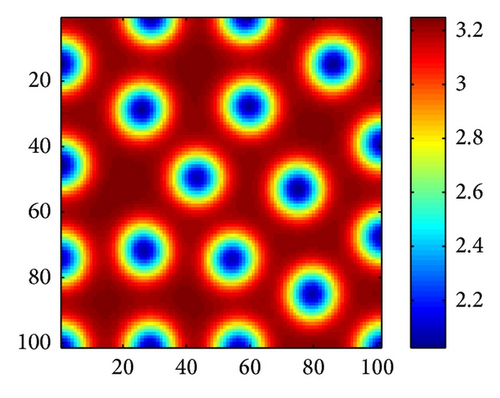
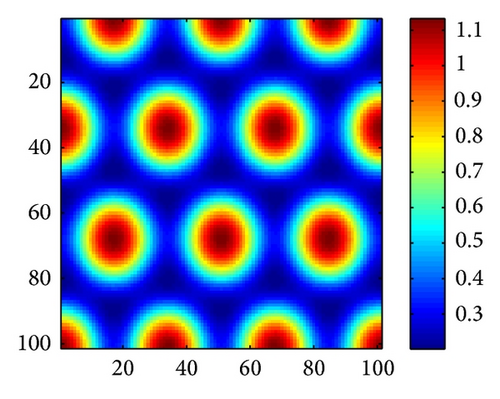
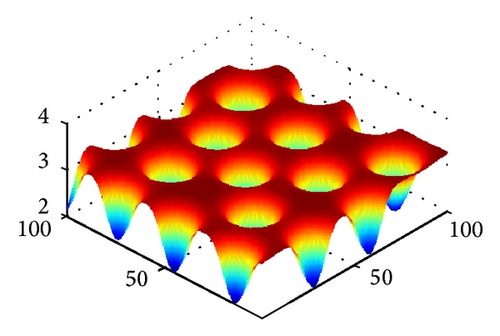
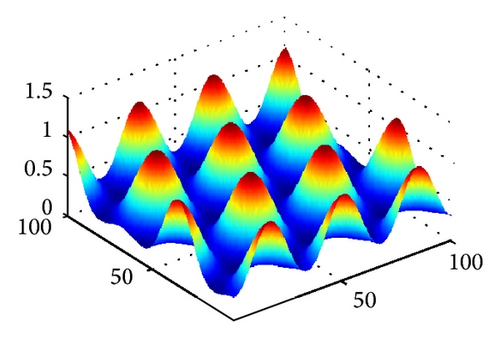
On the other hand, it is easy to check that holes, stripes, and spots also appear in model (4) without time delay for τ = 0 and other the parameters are taken the same way as in Figures 2(a)–2(c), respectively. However, in parameters of Figure 2, trace (M_j) < 0 and det (M_j) > 0 for all j ≥ 0 if the cross-diffusion coefficients d₁₂ = 0 and d₂₁ = 0. That is to say, model (4) is stable in absence of cross-diffusion, and this instability is induced by cross-diffusion.

3.2. Chaotic Pattern Formation Domain II

In this subsection, we will focus on the pattern formation when parameters are located in domain II of Figure 1, the domain of pure Hopf-Turing instability.

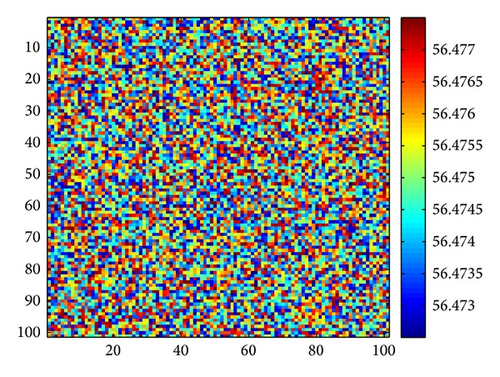
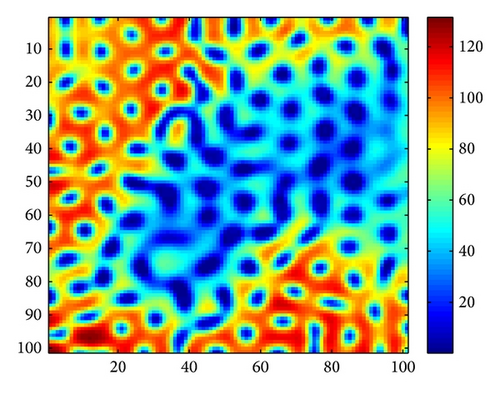
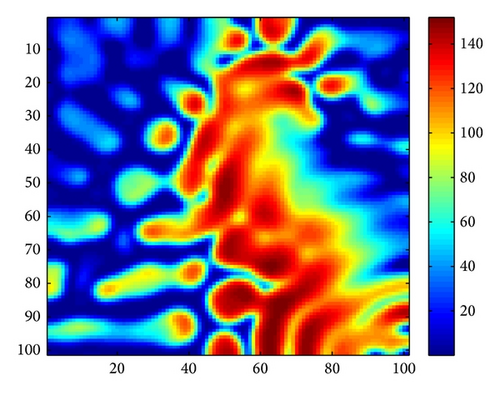
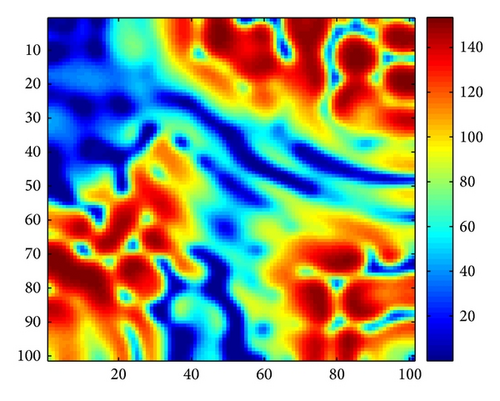
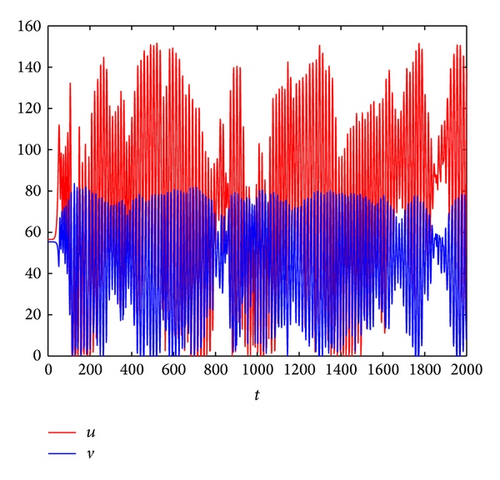
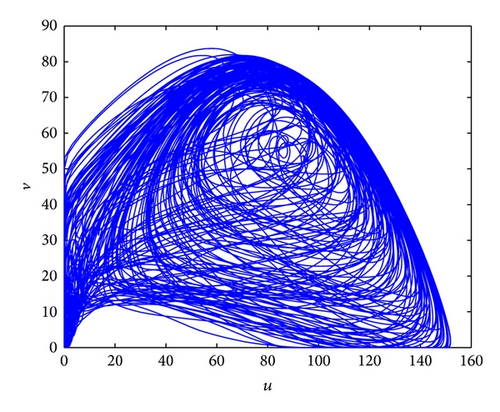
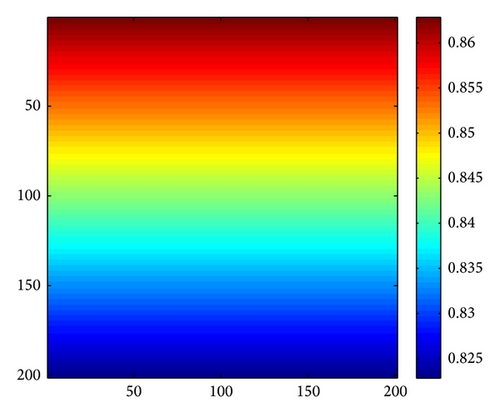
Figure 3 shows the evolution process of the spatial pattern of u at time t = 0,100,1000,2000 with parameter set (25) and a = 0.1, b = 0.71, r = 1.54, d = 0.47, d₁₁ = 0.2, d₂₁ = 0.44, d₂₂ = 0.88, and τ = 0.46. The pattern takes a long time to settle down; starting with a homogeneous state E^* = (56.4750,55.3357) (cf. Figure 3(a)), the random initial distribution leads to the formation of a strongly irregular transient pattern in the domain. After the irregular pattern form (cf. Figure 3(b)), it grows slightly and “jumps” alternately for a certain time, and finally the chaos patterns prevail over the whole domain (cf. Figures 3(c)-3(d)), which is time-dependent. For the sake of learning the spatiotemporal dynamics of model (4) further, we illustrate the time-series plots and phase portraits in Figures 3(e)-3(f). From the time-series plots in Figure 3(e), one can see that u and v strongly oscillates over time t. And in Figure 3(f), there exhibits a “local” phase plane of the system invaded by the irregular spatiotemporal oscillations; the trajectory now fills nearly the whole domain inside the quasi-limit cycle. This regime of the system dynamics corresponds to spatiotemporal chaos. And the spatial symmetry of model (4) is broken, and the patterns are oscillatory in space.

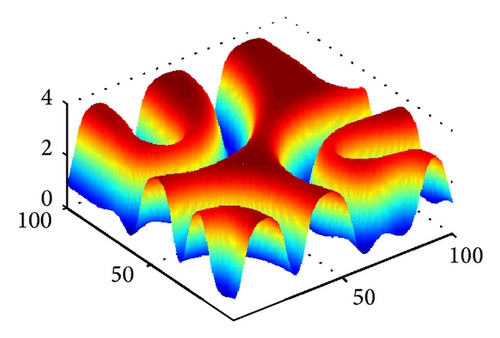
3.3. Spiral Wave Pattern Formation Domain IV

In this subsection, we will focus on the pattern formation when parameters are located in domain IV of Figure 1, the domain of pure Hopf instability.

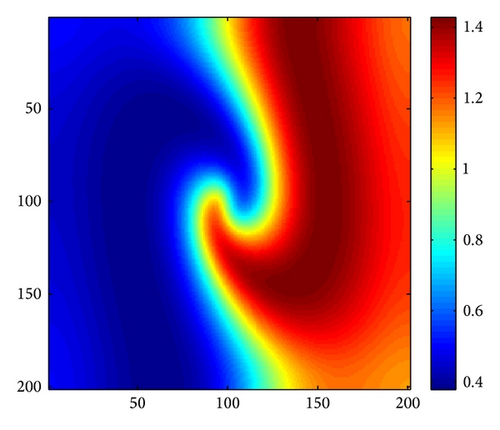
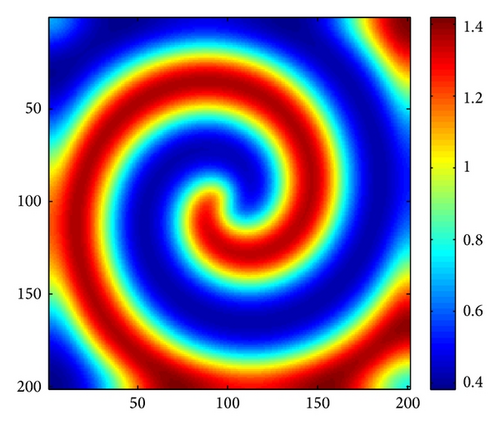
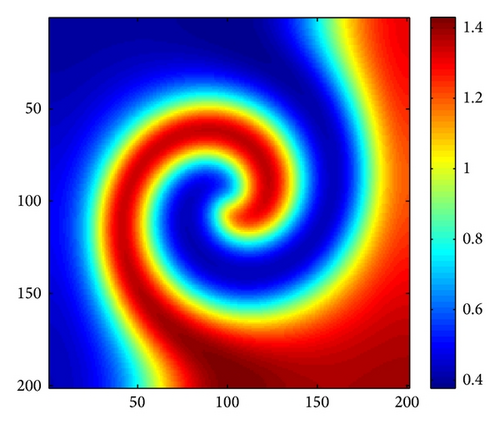
In order to make any influence of the corners of the domain more visible, and thanks to the insightful work of Medvinsky et al. [4] and Upadhyay et al. [54], we have studied the spiral wave pattern for the following initial condition (27). In this case, we employ Δx = Δy = 1 and the system size is 200 × 200.

In order to make any influence of the corner of the domain more visible, following [43, 55], the initial conditions are deliberately chosen to be unsymmetrical as

()

where ε₁ = 2 × 10⁻⁴ and ε₂ = 3 × 10⁻⁴. For more clarity, we put the initial data of prey u as follow

()

Figure 4 shows the evolution process of the spatial pattern of prey u at t = 0,500,1500,3000 with (d, d₂₁, d₂₂) = (0.5,0.15,0.37); the other parameters are fixed as in (25). Figure 4(a) shows that, for the model (4) with initial conditions (27), the formation of the irregular patchy structure can be preceded by the evolution of a regular spiral spatial pattern. Note that the appearance of the spirals is not induced by the initial conditions. The center of each spiral is situated in a critical point (x_cr, y_cr) = (100,100), where u(x_cr, y_cr) = u^*, v(x_cr, y_cr) = v^*. After the spirals form (Figure 4(b)), they grow slightly for a certain time and their spatial structure becomes more distinct (Figures 4(c) and 4(d)). Obviously, spiral pattern arises from Hopf instability.

4. Concluding Remarks

In this paper, we analyze the spatiotemporal dynamics of a spatial Leslie-Gower predator-prey model with time delay and diffusion under the zero-flux boundary conditions. The value of this study is twofold. First, it gives the conditions of Hopf and Turing instability induced by the effects of time delay and cross-diffusion. Second, it gives three domains for three kinds of patterns of model (4) and finds that time delay and cross-diffusion may induce Turing instability, resulting in stationary Turing patterns, Hopf instability, resulting in spiral wave patterns, and Turing-Hopf instability, resulting in chaotic wave patterns.

If τ is small enough, it is worthy to note that, for the delayed model (4), two typical patterns are similar to those in our previous work [43] (a special case of model (4) with self diffusion): pure Turing instability gives birth to the holes, stripes, and spots patterns (cf. Figure 2) and pure Hopf instability to spiral wave pattern (cf. Figure 4). But this is not forever. In the present paper, we find that the delayed reaction-diffusion model (4) exhibits more complex pattern formation, for there exists the third pattern, chaotic wave pattern, which is induced by Turing-Hopf instability. The complexity of the pattern formation is induced by the cross-diffusion effect.

The results of the formation of these patterns may indicate the vital role of phase transience regimes in the spatiotemporal organization of the prey and predator in the real world situation. It is also important to distinguish between “intrinsic” patterns, that is, Turing patterns arising due to predation, and “forced” patterns induced by the heterogeneity of the environment, that is, spiral wave pattern. Because of the environmental heterogeneity, the dispersion of varying quantities and typical times and lengths can be essentially different in different cases and thus can induce different spatial patterns.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

The authors would like to thank the anonymous referee for the very helpful suggestions and comments which led to the improvement of our original paper. This research was supported by the National Science Foundation of China (61373005), Zhejiang Provincial Natural Science Foundation (LY12A01014), and the Fund Project of Zhejiang Provincial Education Department (Y201223449).

References

1 Neuhauser C., Mathematical challenges in spatial ecology, Notices of the American Mathematical Society. (2001) 48, no. 11, 1304–1314, MR1870633.
Google Scholar
2 Cantrell R. S. and Cosner C., Spatial Ecology via Reaction-Diffusion Equations, 2003, John Wiley & Sons, https://doi.org/10.1002/0470871296, MR2191264.
10.1002/0470871296
Google Scholar
3 Nicolis G. and Prigogine I., Self-Organization in Nonequibibrium System, 1997, John Wiley & Sons.
Google Scholar
4 Medvinsky A. B., Petrovskii S. V., Tikhonova I. A., Malchow H., and Li B.-L., Spatiotemporal complexity of plankton and fish dynamics, SIAM Review. (2002) 44, no. 3, 311–370, https://doi.org/10.1137/S0036144502404442, MR1951363.
10.1137/S0036144502404442
Web of Science® Google Scholar
5 Murray J. D., Discussion: turing′s theory of morphogenesis: its influence on modelling biological pattern and form, Bulletin of Mathematical Biology. (1990) 52, no. 1-2, 119–152, 2-s2.0-0001100811, https://doi.org/10.1016/S0092-8240(05)80007-2.
10.1016/S0092-8240(05)80007-2
Web of Science® Google Scholar
6 Gierer A. and Meinhardt H., A theory of biological pattern formation, Biological Cybernetic. (1972) 12, no. 1, 30–39, 2-s2.0-0015454185, https://doi.org/10.1007/BF00289234.
10.1007/BF00289234
CAS PubMed Web of Science® Google Scholar
7 Cross M. C. and Hohenberg P. C., Pattern formation outside of equilibrium, Reviews of Modern Physics. (1993) 65, no. 3, 851–1112, 2-s2.0-12044252828, https://doi.org/10.1103/RevModPhys.65.851.
10.1103/RevModPhys.65.851
CAS Web of Science® Google Scholar
8 Jung P. and Mayer-Kress G., Spatiotemporal stochastic resonance in excitable media, Physical Review Letters. (1995) 74, no. 11, 2130–2133, 2-s2.0-5944229562, https://doi.org/10.1103/PhysRevLett.74.2130.
10.1103/PhysRevLett.74.2130
CAS PubMed Web of Science® Google Scholar
9 Kyrychko Y. N., Blyuss K. B., Hogan S. J., and Schöll E., Control of spatiotemporal patterns in the Gray-Scott model, Chaos. (2009) 19, no. 4, 2-s2.0-74349117230, https://doi.org/10.1063/1.3270048, 043126.
10.1063/1.3270048
CAS PubMed Web of Science® Google Scholar
10 Lee K. J., McCormick W. D., Ouyang Q., and Swinney H. L., Pattern formation by interacting chemical fronts, Science. (1993) 261, no. 5118, 192–194, 2-s2.0-0000037738.
10.1126/science.261.5118.192
CAS PubMed Web of Science® Google Scholar
11 Lindner B., García-Ojalvo J., Neiman A., and Schimansky-Geier L., Effects of noise in excitable systems, Physics Reports. (2004) 392, no. 6, 321–424, 2-s2.0-1142283165, https://doi.org/10.1016/j.physrep.2003.10.015.
10.1016/j.physrep.2003.10.015
Web of Science® Google Scholar
12 Malchow H. and Petrovskii S. V., Dynamical stabilization of an unstable equilibrium in chemical and biological systems, Mathematical and Computer Modelling. (2002) 36, no. 3, 307–319, https://doi.org/10.1016/S0895-7177(02)00127-9, MR1936058.
10.1016/S0895-7177(02)00127-9
Google Scholar
13 Turing A. M., The chemical basis of morphogenesis, Philosophical Transactions of the Royal Society of London B. (1952) 237, no. 641, 37–72.
10.1098/rstb.1952.0012
CAS Web of Science® Google Scholar
14 Nicolis G. and Prigogine I., Biological Invasions: Global Perspective, 1989, John Wiley & Sons.
Google Scholar
15 Higesada S. N. and Kawasaki K., Biological Invasions: Theory and Practice, 1997, Oxford University Press.
10.1093/oso/9780198548522.001.0001
Google Scholar
16 Aziz-Alaoui M. A. and Daher Okiye M., Boundedness and global stability for a predator-prey model with modified Leslie-Gower and Holling-type II schemes, Applied Mathematics Letters. (2003) 16, no. 7, 1069–1075, https://doi.org/10.1016/S0893-9659(03)90096-6, MR2013074.
10.1016/S0893-9659(03)90096-6
Web of Science® Google Scholar
17 Aziz-Alaoui M. A. and Daher Okiye M., V. Capasso, On the dynamics of a predator-prey model with the holling-tanner functional response, Proceedings of the 5th European Conference on Mathematical and Theoretical Biology (ESMTB ′02), 2002, 270–278.
Google Scholar
18 Camara B. I. and Aziz-Alaoui M. A., Dynamics of a predator-prey model with diffusion, Dynamics of Continuous, Discrete & Impulsive Systems A. (2008) 15, no. 6, 897–906, MR2469312.
Google Scholar
19 Camara B. I. and Aziz-Alaoui M. A., Turing and Hopf patterns formation in a predator-prey model with Leslie-Gower-type functional response, Dynamics of Continuous, Discrete & Impulsive Systems B. (2009) 16, no. 4, 479–488, MR2547538.
Google Scholar
20 Camara B., Complexité de dynamiques de modles proie-prédateur avec diffusion et application [Ph.D. thesis], 2009, Universit du Havre.
Google Scholar
21 Guan X. N., Wang W. M., and Cai Y. L., Spatiotemporal dynamics of a Leslie-Gower predator-prey model incorporating a prey refuge, Nonlinear Analysis: Real World Applications. (2011) 12, no. 4, 2385–2395, https://doi.org/10.1016/j.nonrwa.2011.02.011, MR2801027.
10.1016/j.nonrwa.2011.02.011
Web of Science® Google Scholar
22 Ferrara M. and Guerrini L., An economic growth model with power law logistic technology and time delay, Far East Journal of Mathematical Sciences. (2013) 72, no. 1, 169–174.
Google Scholar
23 Bianca C., Ferrara M., and Guerrini L., Hopf bifurcations in a delayed-energy-based model of capital accumulation, Applied Mathematics & Information Sciences. (2013) 7, no. 1, 139–143, https://doi.org/10.12785/amis/070116, MR2998494.
10.12785/amis/070116
Google Scholar
24 Bianca C., Ferrara M., and Guerrini L., The Cai model with time delay: existence of periodic solutions and asymptotic analysis, Applied Mathematics & Information Sciences. (2013) 7, no. 1, 21–27, https://doi.org/10.12785/amis/070103, MR2998481.
10.12785/amis/070103
Google Scholar
25 Ferrara M., A note on convergence speed and population in the AK model with habit formation, International Journal of Pure and Applied Mathematics. (2011) 67, no. 3, 327–335, MR2663739.
Google Scholar
26 Ferrara M., Technological diffusion and Benthamite utility in the Ramsey model: an analytical exploration, International Journal of Pure and Applied Mathematics. (2011) 67, no. 2, 225–236, MR2814733.
Google Scholar
27 Bianca C., Ferrara M., and Guerrini L., High-order moments conservation in thermostatted kinetic models, Journal of Global Optimization. (2013) 1–16, https://doi.org/10.1007/s10898-013-0045-2.
10.1007/s10898-013-0045-2
Web of Science® Google Scholar
28 Wang W. M., Cai Y. L., Zhu Y. N., and Guo Z. G., Allee-effect-induced instability in a reactiondiffusion predator-prey model, Abstract and Applied Analysis. (2013) 2013, 10, 487810, https://doi.org/10.1155/2013/487810.
10.1155/2013/487810
Google Scholar
29 Wang S., Liu W., Guo Z., and Wang W., Traveling wave solutions in a reaction-diffusion epidemic model, Abstract and Applied Analysis. (2013) 2013, 13, https://doi.org/10.1155/2013/216913, 216913, MR3044984.
10.1155/2013/216913
Google Scholar
30 Ruan S., On nonlinear dynamics of predator-prey models with discrete delay, Mathematical Modelling of Natural Phenomena. (2009) 4, no. 2, 140–188, MR2503211.
10.1051/mmnp/20094207
Web of Science® Google Scholar
31 Nindjin A. F., Aziz-Alaoui M. A., and Cadivel M., Analysis of a predator-prey model with modified Leslie-Gower and Holling-type II schemes with time delay, Nonlinear Analysis: Real World Applications. (2006) 7, no. 5, 1104–1118, https://doi.org/10.1016/j.nonrwa.2005.10.003, MR2260902.
10.1016/j.nonrwa.2005.10.003
Web of Science® Google Scholar
32 Yafia R., El Adnani F., and Alaoui H. T., Limit cycle and numerical similations for small and large delays in a predator-prey model with modified Leslie-Gower and Holling-type II schemes, Nonlinear Analysis: Real World Applications. (2008) 9, no. 5, 2055–2067, https://doi.org/10.1016/j.nonrwa.2006.12.017, MR2441766.
10.1016/j.nonrwa.2006.12.017
Web of Science® Google Scholar
33 Xu R. and Chen L., Persistence and stability for a two-species ratio-dependent predator-prey system with time delay in a two-patch environment, Computers & Mathematics with Applications. (2000) 40, no. 4-5, 577–588, https://doi.org/10.1016/S0898-1221(00)00181-4, MR1772656.
10.1016/S0898-1221(00)00181-4
Web of Science® Google Scholar
34 Li Q. S. and Ji L., Control of turing pattern formation by delayed feedback, Physical Review E. (2004) 69, no. 4, 2-s2.0-42749107275, 046205.
10.1103/PhysRevE.69.046205
Web of Science® Google Scholar
35 Hadeler K. P. and Ruan S. G., Interaction of diffusion and delay, Discrete and Continuous Dynamical Systems B. (2007) 8, no. 1, 95–105, https://doi.org/10.3934/dcdsb.2007.8.95, MR2300324.
10.3934/dcdsb.2007.8.95
Web of Science® Google Scholar
36 Ghosh P., Sen S., and Ray D. S., Nonlinear dynamics of finite perturbation: collapse and revival of spatial patterns, Physical Review E. (2009) 79, no. 1, 016206, https://doi.org/10.1103/PhysRevE.79.016206, MR2552205.
10.1103/PhysRevE.79.016206
Web of Science® Google Scholar
37 Sen S., Ghosh P., Riaz S. S., and Ray D. S., Time-delay-induced instabilities in reaction-diffusion systems, Physical Review E. (2009) 80, no. 4, 2-s2.0-70449373358, https://doi.org/10.1103/PhysRevE.80.046212, 046212.
10.1103/PhysRevE.80.046212
Web of Science® Google Scholar
38 Ghosh P., Sen S., and Ray D. S., Reaction-Cattaneo systems with fluctuating relaxation time, Physical Review E. (2010) 81, no. 2, 2-s2.0-77249124419, https://doi.org/10.1103/PhysRevE.81.026205, 026205.
10.1103/PhysRevE.81.026205
Web of Science® Google Scholar
39 Ghosh P., Control of the Hopf-Turing transition by time-delayed global feedback in a reaction-diffusion system, Physical Review E. (2011) 84, no. 1, 2-s2.0-79961118458, https://doi.org/10.1103/PhysRevE.84.016222, 016222.
10.1103/PhysRevE.84.016222
Web of Science® Google Scholar
40 Ghosh P., Sen S., Riaz S. S., and Ray D. S., Controlling birhythmicity in a self-sustained oscillator by time-delayed feedback, Physical Review E. (2011) 83, no. 3, 036205, https://doi.org/10.1103/PhysRevE.83.036205, MR2788258.
10.1103/PhysRevE.83.036205
Web of Science® Google Scholar
41 Zhu Y., Cai Y., Yan S., and Wang W., Dynamical analysis of a delayed reaction-diffusion predator-prey system, Abstract and Applied Analysis. (2012) 2012, 23, https://doi.org/10.1155/2012/323186, 323186, MR2991022.
10.1155/2012/323186
Google Scholar
42 Yan S., Lian X., Wang W., and Wang Y., Bifurcation analysis in a delayed diffusive Leslie-Gower model, Discrete Dynamics in Nature and Society. (2013) 2013, 11, 170501, MR3037728.
10.1155/2013/170501
Web of Science® Google Scholar
43 Lian X. Z., Wang H. L., and Wang W. M., Delay-driven pattern formation in a reaction-diffusion predator-prey model incorporating a prey refuge, Journal of Statistical Mechanics. (2013) 2013, no. 4, P04006.
10.1088/1742-5468/2013/04/P04006
Google Scholar
44 Yan S. L., Lian X. Z., Wang W. M., and Upadhyay R. K., Spatiotemporal dynamics in a delayed diffusive predator model, Applied Mathematics and Computation. (2013) 224, 524–534.
10.1016/j.amc.2013.08.045
Web of Science® Google Scholar
45 Wang W., Lin Y., Zhang L., Rao F., and Tan Y., Complex patterns in a predator-prey model with self and cross-diffusion, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 4, 2006–2015, https://doi.org/10.1016/j.cnsns.2010.08.035, MR2736066.
10.1016/j.cnsns.2010.08.035
Web of Science® Google Scholar
46 Wang W.-M., Wang W.-J., Lin Y.-Z., and Tan Y.-J., Pattern selection in a predation model with self and cross diffusion, Chinese Physics B. (2011) 20, no. 3, 2-s2.0-79955647813, https://doi.org/10.1088/1674-1056/20/3/034702, 034702.
10.1088/1674-1056/20/3/034702
Web of Science® Google Scholar
47 Biktashev V. N., Brindley J., Holden A. V., and Tsyganov M. A., Pursuit-evasion predator-prey waves in two spatial dimensions, Chaos. (2004) 14, no. 4, 988–994, https://doi.org/10.1063/1.1793751, MR2106513.
10.1063/1.1793751
CAS PubMed Web of Science® Google Scholar
48 Shukla J. B. and Verma S., Effects of convective and dispersive interactions on the stability of two species, Bulletin of Mathematical Biology. (1981) 43, no. 5, 593–610, https://doi.org/10.1016/S0092-8240(81)80085-7, MR661520.
10.1016/S0092-8240(81)80085-7
Web of Science® Google Scholar
49 Lian X., Yue Y., and Wang H., Pattern formation in a cross-diffusive ratio-dependent predator-prey model, Discrete Dynamics in Nature and Society. (2012) 2012, 13, 814069, MR3000409.
10.1155/2012/814069
Web of Science® Google Scholar
50 Kerner E. H., Further considerations on the statistical mechanics of biological associations, Bulletin of Mathematical Biophysics. (1959) 21, 217–255, MR0104525.
10.1007/BF02476361
Google Scholar
51 Shigesada N., Kawasaki K., and Teramoto E., Spatial segregation of interacting species, Journal of Theoretical Biology. (1979) 79, no. 1, 83–99, https://doi.org/10.1016/0022-5193(79)90258-3, MR540951.
10.1016/0022-5193(79)90258-3
CAS PubMed Web of Science® Google Scholar
52 Mei Z., Numerical Bifurcation Analysis for Reaction-Diffusion Equations, 2000, 28, Springer, Berlin, Germany, MR1772261.
10.1007/978-3-662-04177-2
Google Scholar
53 Garvie M. R., Finite-difference schemes for reaction-diffusion equations modeling predator-prey interactions in MATLAB, Bulletin of Mathematical Biology. (2007) 69, no. 3, 931–956, https://doi.org/10.1007/s11538-006-9062-3, MR2295839.
10.1007/s11538-006-9062-3
PubMed Web of Science® Google Scholar
54 Upadhyay R. K., Wang W., and Thakur N. K., Spatiotemporal dynamics in a spatial plankton system, Mathematical Modelling of Natural Phenomena. (2010) 5, no. 5, 102–122, https://doi.org/10.1051/mmnp/20105507, MR2681230.
10.1051/mmnp/20105507
Web of Science® Google Scholar
55 Wang W. M., Zhang L., Wang H. L., and Li Z. Q., Pattern formation of a predator-prey system with Ivlev-type functional response, Ecological Modelling. (2010) 221, no. 2, 131–140, 2-s2.0-70549086997, https://doi.org/10.1016/j.ecolmodel.2009.09.011.
10.1016/j.ecolmodel.2009.09.011
Web of Science® Google Scholar

Citing Literature

All articles

Pattern Formation in Predator-Prey Model with Delay and Cross Diffusion

Abstract

1. Introduction