Abstract and Applied Analysis
Volume 2013, Issue 1 141058
Research Article
Open Access

Variable Structure Disturbance Rejection Control for Nonlinear Uncertain Systems with State and Control Delays via Optimal Sliding Mode Surface Approach

Jing Lei, 

Corresponding Author

Jing Lei

School of Mathematics and Computer Science, Yunnan Nationalities University, Kunming 650500, China ynni.edu.cn

Key Laboratory in Software Engineering of Yunnan Province, Kunming 650091, China

Search for more papers by this author
Xin Wang, 

Xin Wang

School of Mathematics and Computer Science, Yunnan Nationalities University, Kunming 650500, China ynni.edu.cn

Search for more papers by this author
Yu-Mei She, 

Yu-Mei She

School of Mathematics and Computer Science, Yunnan Nationalities University, Kunming 650500, China ynni.edu.cn

Search for more papers by this author
Tian-Jun Zhang, 

Tian-Jun Zhang

School of Mathematics and Computer Science, Yunnan Nationalities University, Kunming 650500, China ynni.edu.cn

Search for more papers by this author
First published: 10 November 2013
https://doi.org/10.1155/2013/141058
Academic Editor: Valery Y. Glizer

Abstract

The paper considers the problem of variable structure control for nonlinear systems with uncertainty and time delays under persistent disturbance by using the optimal sliding mode surface approach. Through functional transformation, the original time-delay system is transformed into a delay-free one. The approximating sequence method is applied to solve the nonlinear optimal sliding mode surface problem which is reduced to a linear two-point boundary value problem of approximating sequences. The optimal sliding mode surface is obtained from the convergent solutions by solving a Riccati equation, a Sylvester equation, and the state and adjoint vector differential equations of approximating sequences. Then, the variable structure disturbance rejection control is presented by adopting an exponential trending law, where the state and control memory terms are designed to compensate the state and control delays, a feedforward control term is designed to reject the disturbance, and an adjoint compensator is designed to compensate the effects generated by the nonlinearity and the uncertainty. Furthermore, an observer is constructed to make the feedforward term physically realizable, and thus the dynamical observer-based dynamical variable structure disturbance rejection control law is produced. Finally, simulations are demonstrated to verify the effectiveness of the presented controller and the simplicity of the proposed approach.

1. Introduction

Various approaches have been proposed to solve disturbance rejection problems, such as H∞ control [1], adaptive control [2], internal model control [3], variable structure control (VSC) [4], and optimal control [5–7]. Optimal disturbance rejection appears in a variety of applications, vehicle engine [5], damped systems [6], and spacecraft attitude control [7], for instance. However, in reality, the factor of nonlinearity, uncertainty, or time delay exhibits much influence on practical system [8–19], especially on today’s large information communication system. The factor of nonlinearity, uncertainty, or time delay leads the system and computation to be more complex and difficult to calculate. In addition, it brings discrepancy between the real parameter and the precise one. Therefore, it is necessary to take account of nonlinearity, uncertainty, or time delays in system modeling. In recent years, these issues have been given many attention; for example, see [1, 8–30]. Moreover, there are series techniques appeared to design controllers for such systems. Seeing that it is not an easy work to solve one of these problems, say nothing of concentrating on all of these issues. This study explores a disturbance rejection control design for a nonlinear uncertain time-delay system using the variable structure control approach, for the reason of VSC’s insensitivity to a wide class of uncertainties or disturbances [4, 8, 12, 13, 16, 30–34]. In previous VSC investigations, some reports gave the solutions for uncertain or nonlinear systems, for example, [8, 30, 34]; some gave for the time delay systems [12, 13]; but few appeared to focus on systems of both nonlinear uncertain and time-delay. This paper is different from these bodies of literature. It presents a relative simple VSC solution to a nonlinear uncertain and time-delay system.

It is based on the ideas of the approximating sequence method [25–27] and the finite spectrum assignment approach [20–22]. The contributions of this study are as follows: firstly, the functional transformation method is applied, which transforms the time-delay system to a delay-free one and reduces the original problem from an infinite-dimension space to a finite-dimension one; subsequently, the optimal sliding mode surface (OSMS) is designed by using approximating sequence method, which simplifies the nonlinear OSMS design problem to a linear two-point boundary value (TPBV) one; furthermore, the corresponding compensators are designed in the variable structure disturbance rejection control (VSDC) so that the nonlinearity, uncertainty, and the time-delay effects are entirely compensated consequentially; moreover, the disturbance effect is reduced by the feedforward compensation term; additionally, to realize its physical implementation, a reduced-order observer is constructed to reconstruct the disturbance state vectors, and thus the observer-based dynamical VSDC is produced; finally, the designed VSDC is employed to a quarter-car suspension model which possesses the nonlinear, uncertain, and time-delay properties, and by comparing the system responses with the open-loop system (OLS), the effectiveness and the simplicity of the designed control are demonstrated.

This paper is organized as follows. After an introduction, in Section 2, system description is done. The OSMS and the corresponding VSDC in finite-time horizon are designed in Section 3. In Section 4, the infinite-time horizon ones are given. In Section 5, numerical simulations are illustrated. Concluding remarks are given in Section 6.

2. System Descriptions

Consider the uncertain nonlinear system with state and control delays:
()
where x(t) ∈ ℝn, u(t) ∈ ℝm are state and control vector, respectively; A0, A1 ∈ ℝn×n, B0, B1 ∈ ℝn×m, and D ∈ ℝn×q are constant matrices; τ, σ ∈ ℝ+ are constant control and state delays, respectively; and ϕ(t) ∈ C([−σ, 0], ℝn) is the initial state vector. represents a bounded matching uncertainty produced by the system perturbation or internal disturbance. f(x, t) ∈ C1(ℝn × ℝ, ℝn) is the nonlinearity with f(0, t) = 0 satisfying Lipschitz condition. In this study, control u(t) is assumed unlimited. Meanwhile, the following assumption is needed for the derivation.

Assumption 1. It is assumed that system (1) is spectral controllable.

In system (1), v(t) ∈ ℝq is the external disturbance input whose dynamical characteristic is known and can be described by the following exosystem:

()
where w(t) ∈ ℝp is the disturbance state vector and  G ∈ ℝp×p and F ∈ ℝq×p are constant matrices. The pair (G, F) is observable completely. The initial condition w(0) can be unknown. Exosystem (2) can describe most general disturbances, such as step signal with unknown amplitude, sinusoidal signal with known frequency and unknown amplitude and phase [28], or random signal [29]. Due to the dynamical characteristics of the external disturbances, exosystem (2) may be Lyapunov stable or asymptotically stable; that is, Reμj(G) = 0   or Reμj(G) < 0    (j = 1, 2, …, p), respectively, where μj(·) denote the eigenvalues of a matrix.

In what follows, we will reduce the controller design problem of original system (1) to that of a delay-free one referring to the method proposed in [20] which applied this method to a linear time-delay system. Now, we develop it to the nonlinear time-delay system (1).

Define the following functional transformation:
()
where y is absolutely continuous and therefore differentiable almost everywhere and A is an n × n matrix to be defined. Employing differentiation under the integral, (3) in conjunction with (1) which gives
()
From (4), it is observed that the range of (3) defines an ordinary differential system given by
()
()
If the following definitions are adopted:
()
in which A is referred to as the characteristic matrix equation and the method of its solution can be found in the researches of Fiagbedzi and Pearson [20, 21] and Zheng, Cheng, and Gao [22], and so forth, system (1) is assumed spectral controllable, which implies that system (5a) and (5b) is completely controllable [20]. Actually, here, ; but we choose the denotation f(x, t) instead of in order to simplify the derivation in the rest of the sections. Hence, time-delay system (1) is transformed into the delay-free system (5a) and (5b).

Notice that system (5a) and (5b) is coupled with y and x(y). Indeed, the term f(x, t) is nonlinear. From the previous investigations, it can be seen that by the functional transformation method [20–22], y is admissible to system (5a) and (5b) if and only if x is admissible to system (1). Moreover, the controller stabilizing (1) also stabilizes (5a) and (5b). Based on this idea, in what follows, we will develop this approach to solve the VSDC problem of system (1) through the equivalent delay-free system (5a) and (5b).

First, system (5a) and (5b) will be converted into a regular form. Assume that the uncertainty is matched; that is, there exists , where is of full column rank [34], so that there exists a nonsingular matrix Ξ ∈ ℝn×n such that
()
where and is nonsingular. Then, denote the following nonsingular transformations:
()
where . Via above transformations, system (5a) and (5b) can be converted into the regular form of
()
()
where fi(x, t),   i = 1,2 is the nonlinear and Lipschitz functions with fi(0, t) = 0. The pair (A, B) is controllable and guarantees (M11, M12) controllable. And is the uncertain function, where there exists a vector function , subject to
()
in which ρi(x, t)  (i = 1,2, …, n1) are scalar functions and the components of d(x, t) are less than or equivalent to the relevant components of ρ(x, t), that is,
()
This is supposed a known to be condition to the controller designers [34].

Thereby, we will demonstrate the control law design process of finite-time horizon and infinite-time horizon in Sections 3 and 4, respectively.

3. Design of VSDC in Finite-Time Horizon

This section is to outline the sufficient and necessary condition for the optimality of an optimal sliding mode surface s*(t) subject to the nonlinear dynamical constraint (9a) and (9b). In what follows, we will give the design procedure in two steps: OSMS design and VSDC design.

3.1. Design of OSMS in Finite-Time Horizon

To design a sliding mode surface s(z) = C1z1(t) + C2z2(t) for system (9a) and (9b), treat z2 as a virtual control of system (9a). And respecting the finite-time performance index
()
where and are positive semidefinite matrices, is a positive definite matrix, and (A, C) is assumed observable; the OSMS will be obtained by solving the optimal control problem of system (9a) with performance index (12).

3.1.1. Global OSMS of Nonlinear Systems

Consider the optimal control problem (9a) subject to (12), treating f1(x, t) as an excitation term despite its relationship with y. Thus, the main result of Theorem 2 is achieved.

Theorem 2. Consider the optimal sliding mode surface design problem described by system (1) under disturbance (2) with quadratic performance index (12). The optimal sliding mode surface is existent and unique which is given by

()
where P1(t) is the unique positive definite solution of Riccati matrix differential equation:
()
P2(t) is the unique solution of Sylvester matrix differential equation:
()
and g(t) is the unique solution of the adjoint equation:
()
The optimal state x*(t) is the solution of the closed-loop system:
()

Proof. In analogy to classical linear quadratic regulator optimal control theory from minimum principle, the Hamiltonian for the linear-quadratic control problem (9a) with respect to (10) and (11) becomes

()
which satisfies the canonical equations:
()
()
with the transversality condition:
()
and the control equation:
()
giving
()
along an optimal trajectory. Then, the canonical equations (19) and (20) result in the coupled nonlinear TPBV problem:
()
The virtual optimal control law is (23). The optimal sliding mode surface is defined by
()
For . The objective is to design forcing system trajectories reach sliding mode surface (25).

From (21), it shows that the costate λ has linear relationship with state z1(t). Thus, denote the costate vector

()
where unknown matrices P1(t), P2(t), and continuous function g(t) are to be determined. Differentiating (26) and substituting the first equation of (24) and (26) into the result follow the following equation:
()
Moreover, putting (26) into the second equation of (24) yields the following equation:
()
Equations (27) and (28) are equivalent directly and give the Riccati differential equation (14), Sylvester differential equation (15), and the adjoint differential equation (16). Then, substituting (26) into the optimal sliding mode surface (25) yields
()
From the denotation in (8), the OSMS (29) becomes
()
Replacing y(t) of (30) by that of (3) yields the optimal sliding mode surface (13).

From (23) and (26), it follows the optimal virtual control

()
Substituting (31) into (9a) with (5b) and (8) obtains the closed-loop system (17).

Matrix differential equations (14)–(16) satisfy the conditions of existence and uniqueness which implies that the OSMS (13) is existent and unique. The proof is completed.

3.1.2. Approximations of Sequences of State and Costate Equations

However, noting that (16) and (17) are coupled nonlinear differential equations, they are complex and seldom have analysis solutions. So, the sequence approximation method is adopted to obtain the solutions. Differential equations (16) and (17) can be replaced by sequences of linear time-varying (LTV) approximations [27]:
()
()
Notice that approximation sequences (32) and (33) are represented as inhomogeneous linear differential equations, which have the following solutions given by the variation of constant formula:
()
()
in which Φ(t) denotes the transition matrix generated by , that is,
()

In what follows, with the purpose of proving sequences {g(k)} and , {x(k)} converge to the solution of (16) and (17), and some preliminaries should be carried out.

Firstly, we should arrange the equations in compact forms. Noting that (32) and (33) are equivalent to (34) and (35), respectively, one formula will be chosen for proving. We select the latter giving the proof. In order to simplify the derivation, denote (16) and (17) in a compact form:
()
and combine (32) and (33) in another compact form:
()
where Ψ denotes the state transition matrix corresponding to matrix K1 and the nonlinear function h(·) ∈ C1([t0, tf] × ℝn, ℝn) with h(t, 0) = 0 satisfies the uniformly boundedness condition and the Lipschitz conditions, respectively; that is,
  •  

    (A1) ∥h(t, x)∥ ≤ γ,   for all  x ∈ ℝn,

  •  

    (A2)  ,  for all  x1, x2 ∈ ℝn, where γ is some finite constant and .

Secondly, we will prove approximating sequences (38) convergent to the solution of (37). As a result, Lemma 3 is available.

Lemma 3. Let h(t, x) satisfy (A1) and (A2). Then, the limit of the solution of the approximating sequences (38) on C([t0, tf]; ℝn) converges to the unique solution of (37) on [t0, tf].

Proof. Let

()
Note that ∥Ψ(t0 − t0)∥ = ∥I∥ = 1. Then, ζ ≥ 1. From (38), it follows that
()
With (A2), (5b), and (8), it gives
()
where . The above inequality gives
()
Subsequently,
()
By analogy, it has
()
According to trigonometry inequality, for any j, the following holds:
()
that is, there exists
()
Via the same way, there exists . Hence, lim k→∞ ∥z(k+j)(t) − z(k)(t)∥ = 0. From (5b) and (8), it follows
()
Therefore, {z(k)(t)} and {x(k)(t)} are sequences of Cauchy in Banach space C([t0, tf]; ℝn), respectively. Therefore, z(k)(t) → z(t) on C([t0, tf]; ℝn) and x(k)(t) → x(t) on C([t0, tf]; ℝn). The proof of Lemma 4 is completed.

Thirdly, result of (38) and (37) described by Lemma 3 directly carries out the same result of (32)–(35) and (16)-(17) described by Lemma 4.

Lemma 4. Let f1(x, t) be bounded and Lipschitz continuous in its arguments. Then, the limits of the solutions of the approximating sequences (32) and (33) (or (34) and (35)) on C([t0, tf]; ℝn) globally converge to the unique solutions of (16) and (17), respectively, on [t0, tf].

Last but not least, the main result of OSMS by approximation sequences is got as Theorem 5.

Theorem 5. Given the nonlinear system (1) and the cost functional (12), then the optimal sliding mode surface is given by the limit of the sequence

()
where P1(t) ∈ ℝn×n is the unique positive definite solution of Riccati matrix differential equation (14), P2(t) ∈ ℝn×p is the unique solution of the Sylvester matrix differential equation (15), and g(k)(t) is given by the converged unique solution of the LTV differential equation sequence (32) or (34). The optimal state x*(t) is the solution of the closed-loop system (33) or (35).

Remark 6. Actually, in practice, the limit of lim k→∞ g(k) can be obtained by replacing ∞ with a positive integer M. Relevantly, the following suboptimal sliding mode surface is achieved:

()
corresponding to the following performance index:
()
where M is determined by a small enough error criterion θ > 0 when the following inequality holds:
()

Consequently, we give the algorithm of OSMS.

Algorithm 7. OSMS of system (1).

  •  

    Step 1. Solve P1(t) and P2(t) from (14) and (15). Give some positive real constant θ > 0. Set and k = 1.

  •  

    Step 2. Obtain the kth adjoint vector g(k)(t) from (34).

  •  

    Step 3. Let M = k. Calculate from (35) and s(M) from (49).

  •  

    Step 4. Calculate J(M) from (50).

  •  

    Step 5. When condition (51) is satisfied, stop and output s(M).

  •  

    Step 6. Calculate x(k) from (35).

3.2. Design of VSDC in Finite-Time Horizon

In this section, we will present the VSDC design of finite-time horizon based on the proposed OSMS in the last section.

3.2.1. VSDC Design

To begin with, a trending law should be chosen. As known to all, different variable structure control laws can be designed corresponding to different sliding mode reachable conditions. In this paper, we will adopt the exponential trending law introduced by Gao [30, 34] as follows:
()
where
()
and ki,   εi are parameters to be selected which determine system instant response and convergence speed of the sliding mode reaching, respectively. The related reachable condition should be satisfied:
()
for i = 1,2, …, n1, that is, . For the reason of the reachable condition (54), variable structure control satisfying condition (54) will drive the state trajectories to reach the sliding mode surface in exponential velocity and then remain on it [30, 34]. Consequentially, in the basis of trending law (52), the VSDC is presented as Theorem 8.

Theorem 8. Consider system (1) under disturbance (2) with quadratic performance index (12). The sliding mode surface is given by (13). Then, the state trajectories can reach the sliding mode surface in finite time and remain on it by the variable structure control law:

()

Proof. Differentiating sliding mode surface (29) with respect to time and substituting system (9a) and (9b) into it give

()
Substituting (26) into (25) and putting the result into (52) yield
()
Comparing (56) and (57), the variable structure control law is designed:
()
Replacing z1, z2 in (58) by x of (8) and (3) yields the VSDC (55).

Besides, the reachable condition (54) is verified in what follows. Substituting the VSDC (58) into (56) gives

()
If si > 0, the following holds:
()
for all  i = 1,2, …, n1. Since
()
and ri > 0. Thus, (59) becomes
()
Alternatively, if si < 0, employing the same results,
()
Therefore, combining (62) and (63), the VSDC (55) which satisfies reachable condition , can make the state trajectories reach the sliding mode surface (13) in finite time and remain on it [30, 34]. The proof is completed.

Remark 9. Actually, for the reason in Remark 6, the suboptimal sliding mode surface (SOSMS) (49) can be applied in practice. Thus, the relevant VSDC for SOSMS (49) can be gotten:

()

Remark 10. Summarily, on the ideal sliding mode surface, there exists . And then, putting virtual control (31) into system (9a) yields the ideal sliding mode equations of system (1):

()
At this time, taking s = 0 into VSDC (55) leads to the equivalent control ue(t) of system (1):
()

3.2.2. Closed-Loop Stability Analysis

Select the OSMS function s(z) as a Lyapunov function candidate, that is, V(z) = (1/2)s2(z). Then, the increment of it is . As known, the OSMS satisfies the reachable condition (54), that is, . Thus, is negative definite, which implies limt→∞ z(t) = 0. Moreover, from (3) and (8), it can be proved that x → 0 as z → 0 indicating the closed-loop system states asymptotically stable.

3.2.3. Physical Realization of VSDC

The VSDC u*(t) in (55) contains disturbance state w(t) which is physically unmeasurable. To solve this problem, one can construct a reduced-order observer for disturbance vector so as to reconstruct the disturbance variables [28, 29, 35].

Since rank F = q, there exists an arbitrary matrix H ∈ ℝ(p−q)×p such that Γ = [FT    HT] T ∈ ℝp×p is nonsingular. Note that Π = Γ−1 = [Π1 : Π2], where Π1 ∈ ℝp×q and Π2 ∈ ℝp×(p−q). It is obvious that
()
where In denotes the n-order identity matrix. Consequently, the following result can be obtained.

Theorem 11. Consider system (1) under disturbance (2) with quadratic performance index (12). Respecting the sliding mode surface (13), the dynamical sliding mode control law is given

()
by which the state trajectories can reach the sliding mode surface in finite time and remain on it.

Proof. Defining the nonsingular transformation

()
it gets
()
Introduce a new variable
()
where L is the gain matrix to be selected. Then, differentiating ψ(t) in (71) with respect to time and substituting (70) into it yield the observation state equation:
()
where is the component state to be reconstructed. Note that the other component state can be measured by . On the other hand, from (69), it follows that
()
Thus, substituting the second equation in (72) into (73) yields
()
Relevant to (74), the reduced-order observer can be written as
()
where , represent the observed values of ψ(t), w(t), respectively. Denote the related errors as , . Subtracting (74) from (75) results in the error equation
()

Now, the problem is converted into finding the observer gain L such that error system (76) is asymptotically stable. That the pair (G, F) is observable ensures the pair (FGΠ2, HGΠ2) observable; thus there exists the gain L such that all eigenvalues of matrix (H − LF)GΠ2 can be assigned to the desired position in left-half plane, which guarantees error system (76) exponentially stable. It implies limt→∞ew(t) = 0, that is, . Hence, rewriting VSDC (57) by replacing the disturbance state w by the estimated state of (75):

()
yields the dynamical VSDC (68). The proof is completed.

At this time, the VSDC design in finite-time horizon is completed. In the next section, we will discuss the corresponding results of infinite-time horizon.

4. VSDC Design in Infinite-Time Horizon

To design an OSMC in the infinite-time horizon, regarding the stability situations of exosystem (2), two different performance indexes in infinite-time horizon can be chosen. When the disturbance is asymptotically stable, that is, Reμj(G) < 0, the following general one should be selected:
()
where is a positive semidefinite matrix, is a positive definite matrix, and (A, C) is observable. On the other hand, when the disturbance is Lyapunov stable, that is, Reμj(G) = 0, since z2 in (78) concluding disturbance w may make the general infinite-horizon performance index (78) not convergent, in this case, the following average one can be selected:
()

Then, our object is to design OSMS and VSDC with respect to performance index (78) and (79) subject to dynamic constraint (9a) and (9b).

In reality, when tf → ∞, the time-variable matrices P1(tf) and P2(tf) of finite-time horizon approach to some constant matrices denoted by P1 and P2, respectively, that is, and [35]. Therefore, the results of the infinite-time horizon can be directly obtained from those of the finite-time horizon. Yet, for the sake of briefness, the corresponding results are omitted here.

5. Simulation Example

In this section, a 2DOF quarter-car model is applied to simulate the system responses under the designed VSDC comparing with those of OLS. The governing dynamic equations are
()
where ms is the sprung mass representing car chassis; mu is the unsprung mass representing wheel assembly; k1s is the linear stiffness coefficients; bs is the damping of the uncontrolled suspension; kt stands for the stiffness of tire respectively; xs, xu are displacements of sprung and unsprung masses, respectively; xr is the road displacement input. The actuator force u acts between sprung and unsprung masses. Let k2s represent the spring nonlinearity and Δms, and let  Δki  (i = 1s, 2s, t) indicate the uncertainty parameters of spring mass, stiffness of spring, and tire with known bounds. Summarizing equations (80), one can get the nonlinearity fi(x)  (i = 1, 2) of the system, which was employed in some references, for example, [14, 15]
()
and the uncertainties Δfi(x) of the system which are referred to [16–18]:
()
More characteristic details about these kinds of nonlinearity and uncertainties can be found in abovementioned [14–18]. By defining the set of state variable
()
where x1 is the suspension deflection, x2 the tire deflection, x3 the sprung mass velocity, and x4 the unsprung mass velocity, the state vector is denoted by x(t) = [x1(t), x2(t), x3(t), x4(t)] T. Then, the vehicle suspension system is rewritten in state-space representation (1) with
()
Adopting the parameter values listed in Table 1 [19], the associated matrices and vectors of (84) are as follows:
()
Table 1. Parameters and values of quarter-car suspension.
Variable Value Unit
ms 350 kg
mu 59 kg
k1s 14500 N/m
k2s 160000 N/m
kt 190000 N/m
bs 1100 N · s/m
Set the initial value x0 = [1,0.1,0.1,0.1]T and time-delays τ = 0.01s, σ = 0.02s. Take , Δki = kidlδl for i = 1s, 2s, t;  l = k1s, k2s, kt, where dl indicates the percentage of variation allowed around its nominal value and δj  (j = ms, k1s, k2s, kt) determine the actual parameter derivation changing in interval [0, 1] [18]. Referring to [16, 17], given the possible variations of uncertain parameters: , , , and , note they represent 28.5% uncertainty in ms, 15% in k1s and k2s, and 25% in kt, which yields the uncertainty bound parameters: Δms ≤ 100 kg, Δk1s ≤ 2175 N/m, Δk2s ≤ 24000 N/m, Δkt ≤ 47500 N/m. Consequentially, the bound vector function ρ is produced:
()

Then, transform the system in the form of (9a) and (9b). To simulate the road profiles, two cases of sinusoidal signal and attenuated signal are employed.

Case 1. Consider sinusoidal disturbance described by exosystem (2) with

()
which produces the eigenvalues of G are ±1j,  ± 1.4142j. Take the performance index (79) with Q = R = I2. First of all, with (14) and (15) the matrices P1, P2 are computed. Moreover, from (32) and (33), g(M) and x(M) are solved. Consequentially, setting k = 1 and ε = 0.05 in trending law (52), the OSMS (49) is gotten as well as VSDC (77) is obtained. Finally, the suspension responses by VSDC and OLS are demonstrated in Figures 1 and 2.

Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
States trajectories of VSDC and OLS under sinusoidal disturbance.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
States trajectories of VSDC and OLS under sinusoidal disturbance.
Details are in the caption following the image
Figure 1 (c)
Open in figure viewerPowerPoint
States trajectories of VSDC and OLS under sinusoidal disturbance.
Details are in the caption following the image
Figure 1 (d)
Open in figure viewerPowerPoint
States trajectories of VSDC and OLS under sinusoidal disturbance.
Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Control inputs and sliding mode surface under sinusoidal disturbance.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Control inputs and sliding mode surface under sinusoidal disturbance.
Details are in the caption following the image
Figure 2 (c)
Open in figure viewerPowerPoint
Control inputs and sliding mode surface under sinusoidal disturbance.

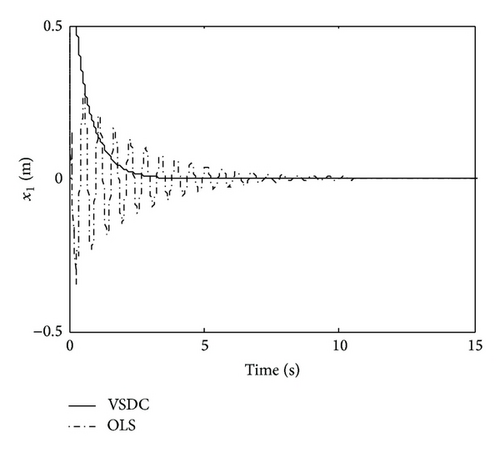
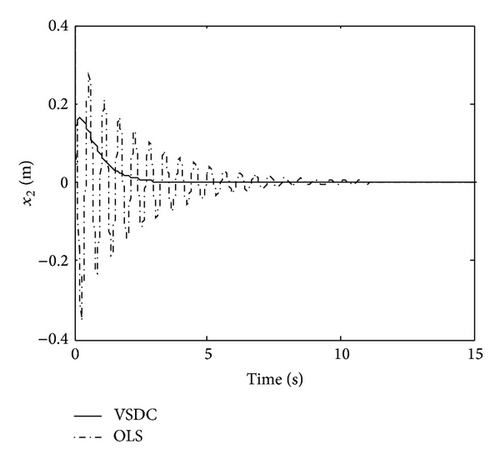
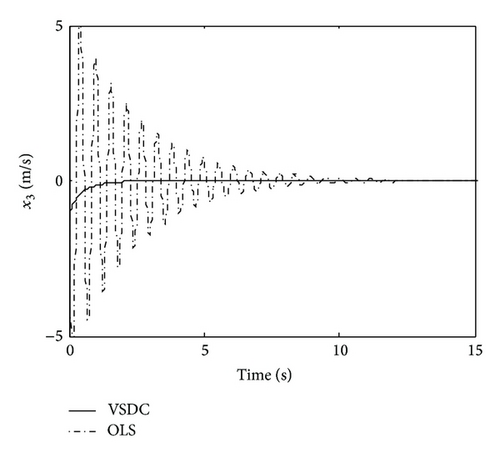
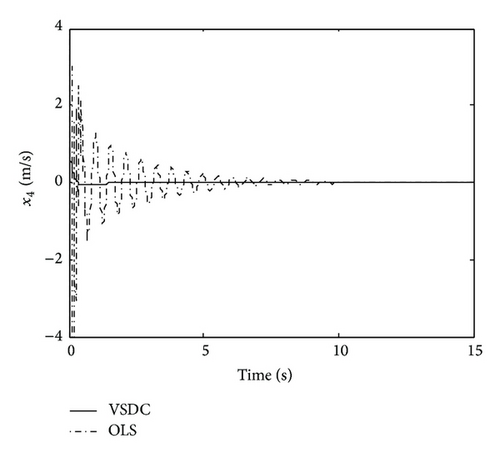
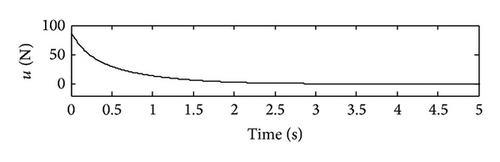
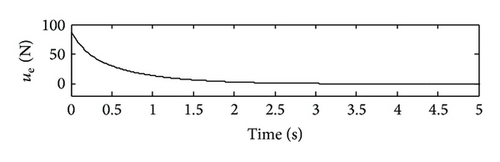
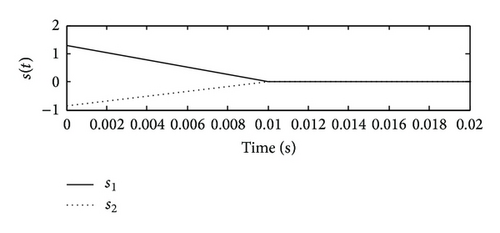
From Figure 1, it can be seen that the states are stabilized and become stable by using VSDC and the magnitudes of the suspension response are obviously reduced comparing with those of the OLS. The reason can be concluded from Figure 2, that by using VSDC, the states were controlled towards the OSMS; while being forced onto the OSMS, the equivalent control ue drove them stabilized and hold good dynamical characteristics.

Case 2. Consider attenuated disturbance described by exosystem (2) with

()
which yields that the eigenvalues of G are −0.2 ± 0.1j,  −0.15 ± 0.5635j. Take performance index (12) with Q =   R =   I2. Through the same way, from (14) and (15), it yields the values of matrix P1, P2. And from (32) and (33), g(M) and x(M) are solvable. Then, the OSMS (49) and VSDC (77) are obtained taking k = 1 and ε = 0.05 in trending law (52). Hence, as displayed in Figures 3 and 4, the suspension responses by VSDC and OLS are illustrated.

Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
States trajectories of VSDC and OLS under attenuated disturbance.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
States trajectories of VSDC and OLS under attenuated disturbance.
Details are in the caption following the image
Figure 3 (c)
Open in figure viewerPowerPoint
States trajectories of VSDC and OLS under attenuated disturbance.
Details are in the caption following the image
Figure 3 (d)
Open in figure viewerPowerPoint
States trajectories of VSDC and OLS under attenuated disturbance.
Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
Control inputs and sliding mode surface under attenuated disturbance.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
Control inputs and sliding mode surface under attenuated disturbance.
Details are in the caption following the image
Figure 4 (c)
Open in figure viewerPowerPoint
Control inputs and sliding mode surface under attenuated disturbance.

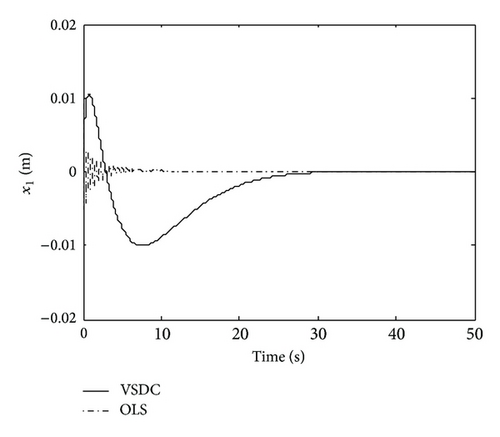
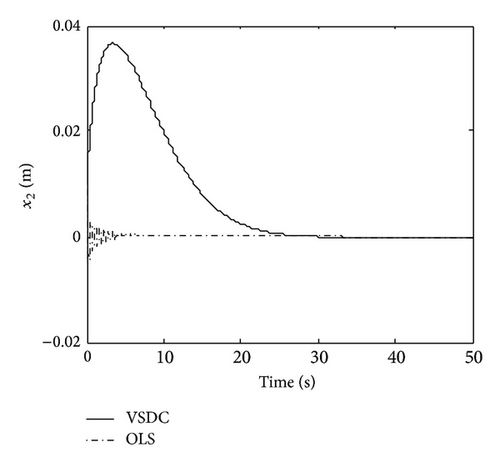
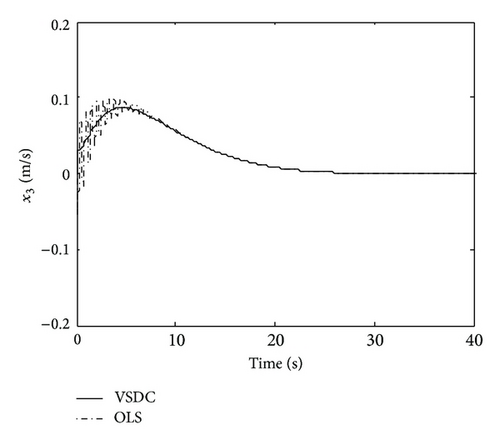
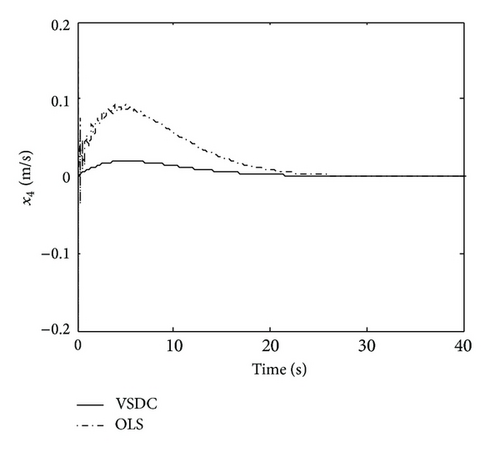
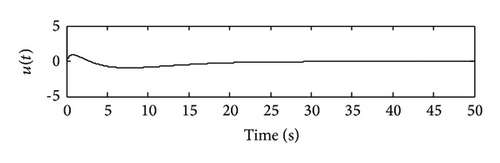
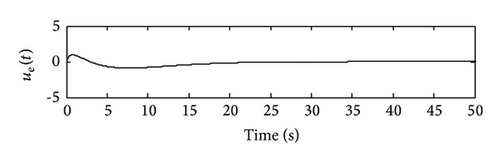
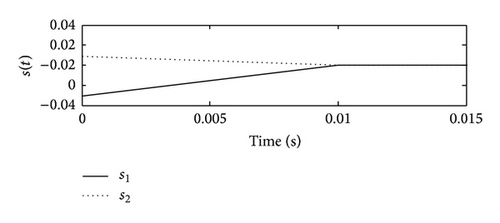
It is shown that the state variables are reduced by VSDC comparing with OLS, which are controlled asymptotically stable at about 30 sec. Clearly, the VSDC rejected the disturbance which is faced by the system and makes the state variable of OLS vibrate.

Summarily, comparing the simulation results between Figures 1 and 2 and Figures 3 and 4, we can see that, although the states are reduced by VSDC and lower than those of OLS when facing sinusoidal disturbance, it still vibrates a little; whereas when facing attenuated disturbance, they converge to zero gradually. The reason lies in the main different feature of these two kinds of signals. Notice that in VSDC (55), there exists the feedforward compensation term described as , which causes the closed-loop system to still be affected by disturbance w(t). For this reason, facing sinusoidal disturbance, the VSDC is able to compensate the effect generated by disturbance so that the state amplitudes are reduced but is not able to eliminate it entirely; while when facing attenuated disturbance, the disturbance effect can be entirely eliminated and state variables approach zero. In addition, the sinusoidal and random disturbances can be entirely eliminated by using dynamic internal-model compensator, which can be referred to some bodies of literature, for example, [35] or our previous studies [28, 36].

6. Conclusions

In this paper, the variable structure disturbance rejection strategy for nonlinear systems with uncertainty and time delay is presented. The original system has been transformed into the delay-free one as well as the optimal problem has been reduced to that of lower dimensions. The designed OSMS and VSDC in both finite-time and infinite-time horizon are proposed, where the disturbance is reduced and the uncertainty and the nonlinearity are entirely compensated. Numerical simulations have demonstrated the effectiveness of the designed control law as well as the simplicity of the proposed approach. It is verified that this proposed approach is easy to implement and of reduced complexity.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

    Acknowledgments

    This work is partially supported by the National Natural Science Foundations (61364012, 11361076), the China Scholarship Council Foundation (201208535084), the Natural Science Foundation of Yunnan Province (2011FZ169), the Key Program of the Scientific Research Foundation of the Education Department of Yunnan Province (2013Z034), and the Open Fund of Key Laboratory in Software Engineering of Yunnan Province (2011SE15). The authors would like to thank Editor Valery Y. Glizer and the Reviewers for their careful review and significant comments improving the presentation of this paper.

        The full text of this article hosted at iucr.org is unavailable due to technical difficulties.