International Journal of Engineering Mathematics
Volume 2013, Issue 1 132827
Research Article
Open Access

Mathematical Modeling and Analysis of the Kinetics of Thermal Inactivation of Enzyme

S. P. Ananthi, 

S. P. Ananthi

Department of Mathematics, The Madura College, Madurai, Tamilnadu 625011, India maduracollege.org

Search for more papers by this author
P. Manimozhi, 

P. Manimozhi

Department of Mathematics, The Madura College, Madurai, Tamilnadu 625011, India maduracollege.org

Search for more papers by this author
T. Praveen, 

T. Praveen

Department of Mathematics, The Madura College, Madurai, Tamilnadu 625011, India maduracollege.org

Search for more papers by this author
A. Eswari, 

A. Eswari

Department of Mathematics, The Madura College, Madurai, Tamilnadu 625011, India maduracollege.org

Department of Mathematics, Sri Ramakrishna Institute of Technology, Coimbatore, Tamilnadu 641010, India srit.org

Search for more papers by this author
L. Rajendran, 

Corresponding Author

L. Rajendran

Department of Mathematics, The Madura College, Madurai, Tamilnadu 625011, India maduracollege.org

Search for more papers by this author
First published: 12 August 2013
https://doi.org/10.1155/2013/132827
Academic Editor: Yurong Liu

Abstract

A theoretical model of Illeova et al. (2003) thermal inactivation of urease is discussed. Analytical expressions pertaining to the molar concentrations of the native and denatured enzyme are obtained in terms of second-order reaction rate constant. Simple and closed form of theoretical expression pertains to the temperature are also derived. In this paper, homotopy analysis method (HAM) is used to obtain approximate solutions for a nonlinear ordinary differential equation. The obtained approximate result in comparison with the numerical ones is found to be in satisfactory agreement.

1. Introduction

Urease is a good catalyst for the hydrolysis of urea. Several excellent techniques are available to assess urease activity [1, 2]. In 1926, urease was isolated by Summner from the seeds of jack bean as a pure, crystalline enzyme [3]. These crystals, the first obtained for a known enzyme, played a decisive role in proving the protein nature of enzymes. Approximately 50 years later, jack bean urease was identified as the first nickel metalloenzyme [4]. A method for the determination of mercury (II) ions at trace levels is described. The method is based on the profound inhibitory effect of mercury on the enzyme urease [5]. For unknown reasons some seeds are particularly rich sources of urease, and this enzyme has been extensively studied in seeds of various Leguminosae, Cucurbitaceae, Asteraceae and Pinaceae [6, 7]. Jack bean urease, which is the most widely used plant urease, is a nickel containing oligomeric enzyme exhibiting a high degree of specificity to urea [8]. Numerous papers have been published on the applications of urease in biotechnology, including the determination of urea for analytical and biomedical purposes and analysis of heavy metal content in natural drinking water and surface water [9]. Hirai et al. [10] study the structural change of jack bean urease induced by addition of synchrotron radiation. Lencki et al. [11] discuss the effect of subunit dissociation, denaturation, aggregation, coagulation, and decomposition on enzyme inactivation kinetics. Omar and Beauregard [12] investigate the unfolding of jack bean urease by fluorescence emission spectroscopy.

To our knowledge, no rigorous analytical expressions of molar concentrations of the native enzyme, denatured enzyme, and temperature for thermal inactivation of urease for the parameters k+1, , , , h, TB, and K have been reported. The purpose of this communication is to derive simple approximate analytical expression for the nonsteady-state concentrations for thermal inactivation of urease using Homotopy analysis method.

2. Mathematical Formulation of Analysis and Problems

Equation (1) illustrates a three-step mechanism of inactivation with a dissociation reaction of the native form of the enzyme, N, into a denatured form, D, and with two parallel association reactions of the native and denatured forms into irreversibly denatured enzyme forms I1 and I2, respectively:
()
where k+1, k−1, k2, and k3 represent the rate constants of individual reactions. The material balances equations for N and D and temperature are given as follows [1]:
()
where cN and cD are the molar concentrations of the native and denatured enzyme form and T is the temperature. The initial boundary condition is
()

3. Concentrations of Native Enzyme Form, Denatured Enzyme Form, and Temperature under Nonsteady State Condition

A powerful, easy-to-use analytic tool for nonlinear problems in general, namely, the homotopy analysis method. This analytic solution agrees well with numerical results and can be regarded as a definition of the solution of the considered nonlinear problem [13]. The homotopy analysis method (HAM) provides an analytical solution in terms of an infinite power series. In order to investigate the accuracy of the solution with a finite number of terms, the system of differential equations was solved. This method is a good technique when comparing to perturbation method and the numerical simulation. Homotopy analysis method has many advantages since it doesn’t rely on a special small parameter [14]. The results reveal that the method is very effective and simple. The method contains the auxiliary parameter ℏ, which provides us with a simple way to adjust and control the convergence region of solution series [15, 16]. Homotopy analysis method provides a powerful tool to strongly analyze linear and nonlinear problems [17, 18]. In this paper, homotopy analysis method (see Appendix A) is used to solve nonlinear differential equations. The analytical expression of molar concentrations of N, D, and temperature (see Appendices A and B) are
()
()
()
These equations represent the new analytical expression of the molar concentrations of the native enzyme, denatured enzyme, and temperature for various values of the parameters k+1, , , , h, TB, and K.

4. Numerical Simulation

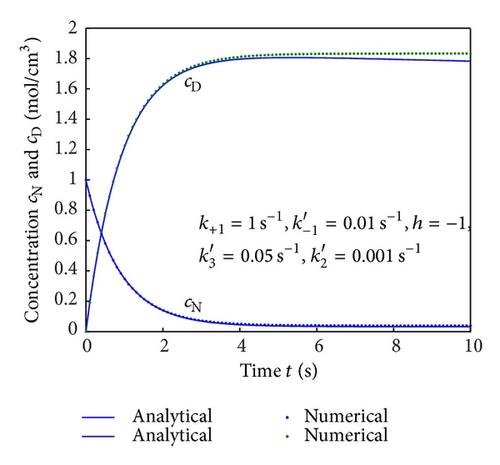
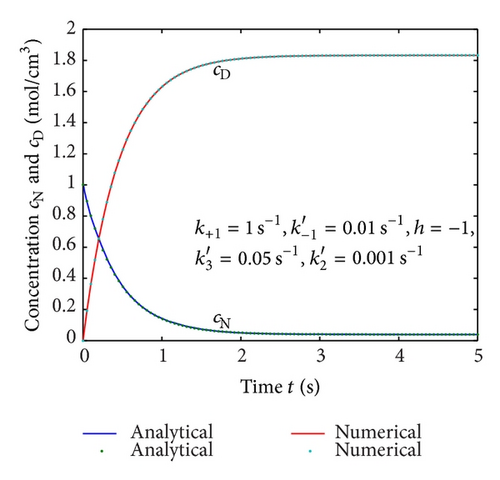
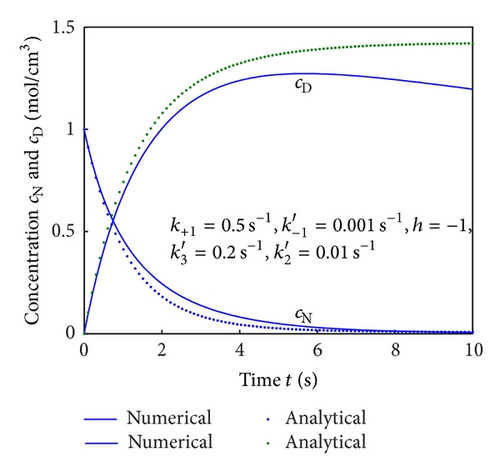
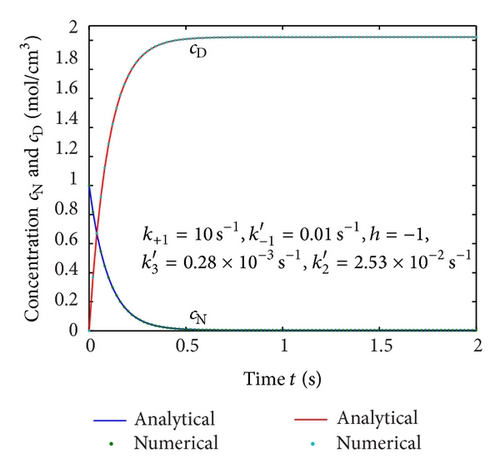
To show the efficiency of the present method, our nonsteady-state result is compared with numerical solution. Equations (4) and (5) are also solved by numerical method using Matlab/Scilab program. The Scilab/Matlab program [19] is also given in Algorithm 1. The numerical values of parameters employed in Illeova et al. [1] and in this study are given in Table 1. The numerical solution is compared with our analytical result in Figures 1(a)–1(e).

Table 1. Range of parameters used in Illeova et al. [1] and this work.
Parameters Range of parameters in [1] Value of the parameter in this work
Figures 1(a)–1(d) Figure 1(e) Figure 2(a) Figure 2(b) Figure 2(c) Figure 3
k+1 s−1 (8.51 ± 0.29) × 10−1 1, 10   1–100 8.80 × 10−1
  • 3.80 × 10−2 to
  • 8.80 × 10−1
 0.01–1.5
(8.36 ± 0.28) × 101 0.01   0.01 1.64–8.64 × 101 8.64 × 101 0.1
(1.74 ± 0.79) × 10−2 0.001–0.0253   —     2.66 × 10−4
(0.24 ± 0.04) × 10−3 0.00028–0.05   10−3 0.28 × 10−3 0.28 × 10−3 10−3
K s−1 4.44 × 10−2   4.44 × 10−2        
TB °C 55–87.5   55–87.5        
    Algorithm 1: Scilab/Matlab program to find the numerical solution of (2) and (3).

  • function main1

  • options= odeset (‘RelTol’,1e-6,‘Stats’,‘on’);

  • %initial conditions

  • T=100;

  • Xo = [1; 0; T+30];

  • tspan = [0,10];

  • tic

  • [t,X] = ode45(@TestFunction,tspan,Xo,options);

  • toc

  • figure

  • hold on

  • plot(t, X(:,1))

  • plot(t, X(:,2))

  • plot(t, X(:,3),‘.’)

  • legend(‘x1’,‘x2’,‘x3’)

  • ylabel(‘x’)

  • xlabel(‘t’)

  • return

  • function [dx_dt]= TestFunction(t,x)

  • k1=2;k2=0.1;k3=10∧(-3);k4=2.66*10∧(-3);K=4.44*10∧(-2);T=100;

  • dx_dt(1) =-k1*x(1)+k2*x(2)∧2-2*k3*x(1)∧2;

  • dx_dt(2) =2*k1*x(1)-2*(k2+k4)*x(2)∧2;

  • dx_dt(3)=K*(T-x(3));

  • dx_dt = dx_dt’;

  • return

Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
(a–d) Molar concentrations of N and D versus time t for various values of the parameters k+1, , , and . Solid lines represent the analytical solution presented in this work ((4) and (5)) and dotted lines represent the numerical solution. (e) Temperature T versus time t for various values of TB when K = 4.44 × 10−2 s−1.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
(a–d) Molar concentrations of N and D versus time t for various values of the parameters k+1, , , and . Solid lines represent the analytical solution presented in this work ((4) and (5)) and dotted lines represent the numerical solution. (e) Temperature T versus time t for various values of TB when K = 4.44 × 10−2 s−1.
Details are in the caption following the image
Figure 1 (c)
Open in figure viewerPowerPoint
(a–d) Molar concentrations of N and D versus time t for various values of the parameters k+1, , , and . Solid lines represent the analytical solution presented in this work ((4) and (5)) and dotted lines represent the numerical solution. (e) Temperature T versus time t for various values of TB when K = 4.44 × 10−2 s−1.
Details are in the caption following the image
Figure 1 (d)
Open in figure viewerPowerPoint
(a–d) Molar concentrations of N and D versus time t for various values of the parameters k+1, , , and . Solid lines represent the analytical solution presented in this work ((4) and (5)) and dotted lines represent the numerical solution. (e) Temperature T versus time t for various values of TB when K = 4.44 × 10−2 s−1.
Details are in the caption following the image
Figure 1 (e)
Open in figure viewerPowerPoint
(a–d) Molar concentrations of N and D versus time t for various values of the parameters k+1, , , and . Solid lines represent the analytical solution presented in this work ((4) and (5)) and dotted lines represent the numerical solution. (e) Temperature T versus time t for various values of TB when K = 4.44 × 10−2 s−1.

5. Discussions

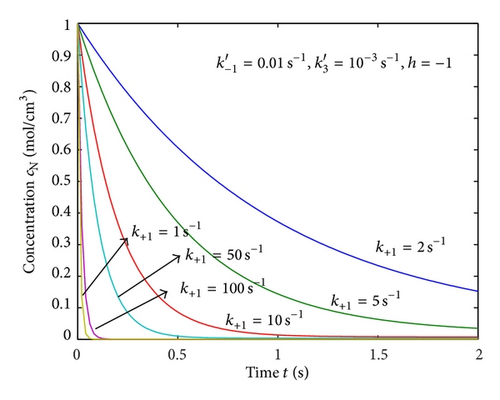
Equations (4) and (5) represent the closed form of an analytical expression of concentrations of native and denatured enzyme for all values of parameters. In Figures 1(a)–1(e), the analytical results are compared with numerical results for various values of parameters and satisfactory agreement is noted. Figures 1(a)–1(d) represent the molar concentrations for various values of rate constant. From the figure, it is inferred that, when time increases the concentration of cN decreases whereas the concentration of cD increases. The time taken to reach the maximum value of cD is the same as the time taken to reach the minimum value of cN. The steady value of cD and cN depends upon the rate constants.

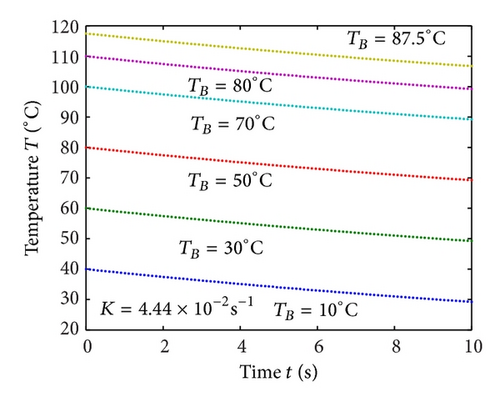
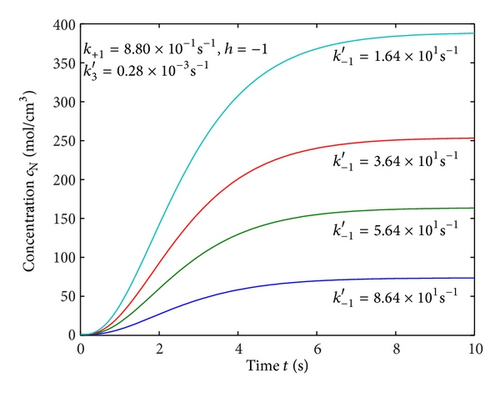
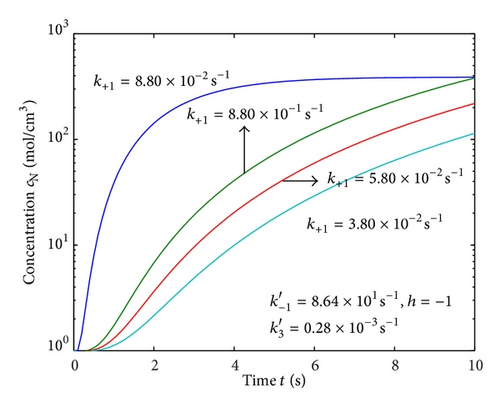
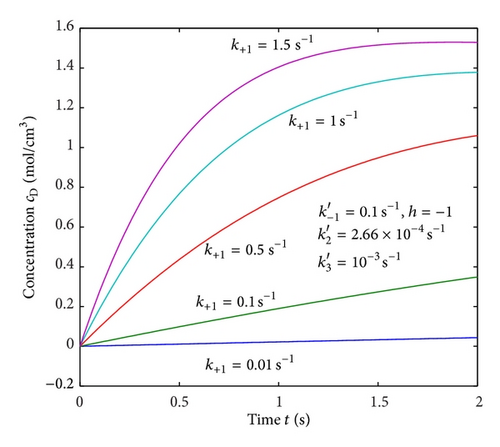
Figures 2(a)–2(c) represent the molar concentration of N versus time t for various values of rate constant k+1 and . From that figure, it is observed that, cN increases when k+1 and increase. Figure 3 represents the molar concentration of D versus time t for various values of parameter k+1. From this figure, it is found that, the value of concentration cD initially increases and reaches the steady state value when t ≥ 5. The concentration cD increases when k+1 increases. The concentration becomes zero when k+1 ≤ 0.01 s−1. Figure 1(e) denotes the representation temperature T versus time t for various values of TB. The value of temperature increases when TB increases. It is almost linear with respect to time t.

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
(a) Molar concentration of N versus time t using (4) for various values of k+1 when  s−1,  s−1, and h = −1. (b) Molar concentration of N versus time t using (4) for various values of when k+1 = 8.80 × 10−1 s−1,  s−1, and h = −1. (c) Molar concentration of N versus time t using (4) for various values of k+1 when  s−1,  s−1, and h = −1.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
(a) Molar concentration of N versus time t using (4) for various values of k+1 when  s−1,  s−1, and h = −1. (b) Molar concentration of N versus time t using (4) for various values of when k+1 = 8.80 × 10−1 s−1,  s−1, and h = −1. (c) Molar concentration of N versus time t using (4) for various values of k+1 when  s−1,  s−1, and h = −1.
Details are in the caption following the image
Figure 2 (c)
Open in figure viewerPowerPoint
(a) Molar concentration of N versus time t using (4) for various values of k+1 when  s−1,  s−1, and h = −1. (b) Molar concentration of N versus time t using (4) for various values of when k+1 = 8.80 × 10−1 s−1,  s−1, and h = −1. (c) Molar concentration of N versus time t using (4) for various values of k+1 when  s−1,  s−1, and h = −1.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Molar concentration of D versus time t using (5) for various values of k+1 when  s−1,  s−1,  s−1, and h = −1.

6. Conclusion

In this work, we obtained the analytical expression of concentrations in terms of rate constants k+1, , , , bath temperature TB, and coefficient in the enthalpy balance K. The nonlinear ordinary differential equations have been solved analytically. The closed analytical expressions of molar concentrations of cN, cD, and temperature T are obtained using the homotopy analysis method. An agreement with the numerical result is noted. The information gained from this theoretical model can be useful for the kinetic analysis of the experimental results over handling rate constants and molar concentrations.

Nomenclature

  • cN:
  • Molar concentration of the native enzyme form (mole/cm3)
  • cD:
  • Molar concentration of the denatured enzyme form (mole/cm3)
  • k+1, k−1, k2, k3:
  • Rate constants of individual reaction (s−1)
  • , , :
  • Modified rate constants (s−1)
  • K:
  • Coefficient in the enthalpy balance (s−1)
  • TB:
  • Bath temperature (K)
  • T:
  • Temperature (K)
  • t:
  • Time (s).

    • Acknowledgments

    This work was supported by the Council of Scientific and Industrial Research (CSIR no. 01(2442)/10/EMR-II), the Government of India. The authors are thankful to Dr. R. Murali, the Principal, The Madura College, Madurai, and Mr. S. Natanagopal, the Secretary, Madura College Board, Madurai for their encouragement. It is a pleasure to thank the referees for their valuable suggestions.

      Appendices

      A. Basic Concept of Homotopy Analysis Method

      Consider the following differential equation [20–22]:
      ()
      where N is a nonlinear operator, t denotes an independent variable, and u(t) is an unknown function. For simplicity, we ignore all boundary or initial conditions, which can be treated in a similar way. By means of generalizing the conventional homotopy method, Liao [19] constructed the so-called zero-order deformation equation as follows:
      ()
      where p ∈ [0,1] is the embedding parameter, h ≠ 0 is a nonzero auxiliary parameter, H(t) ≠ 0 is an auxiliary function, L is an auxiliary linear operator, u0(t) is an initial guess of u(t), and φ(t : p) is an unknown function. It is important that one has great freedom to choose auxiliary unknowns in HAM. Obviously, when p = 0 and p = 1, it holds the following:
      ()
      respectively. Thus, as p increases from 0 to 1, the solution φ(t; p) varies from the initial guess u0(t) to the solution u(t). Expanding φ(t; p) in Taylor series with respect to p, we have
      ()
      where
      ()
      If the auxiliary linear operator, the initial guess, the auxiliary parameter h, and the auxiliary function are so properly chosen and the series (A.4) converges at p = 1, then we have
      ()
      Differentiating (A.2) for m times with respect to the embedding parameter p, and then setting p = 0 and finally dividing them by m!, we will have the so-called mth-order deformation equation as follows:
      ()
      where
      ()
      Applying L−1 on both sides of (A.7), we get
      ()
      In this way, it is easily to obtain um for m ≥ 1, at Mth order, we have
      ()
      When M → +∞, we get an accurate approximation of the original equation (A.1). For the convergence of the above method, we refer the reader to Liao [13]. If (A.1) admits unique solution, then this method will produce the unique solution. If (A.1) does not possess unique solution, the HAM will give a solution among many other (possible) solutions.

      B. Approximate Analytical Solutions of the System of (2) Using Homotopy Analysis Method

      In this appendix, we indicate how (4) and (5) in this paper are derived. The homotopy analysis method was constructed to determine the solution of (2)
      ()
      In order to solve (B.1) by means of the HAM, we first construct the zeroth-order deformation equation by taking H(t) = 1,
      ()
      subject to the following initial conditions:
      ()
      ()
      where p ∈ [0,1] is an embedding parameter and h ≠ 0 is the so-called convergence control parameter. When p = 0
      ()
      From (B.5) and initial condition (B.3), we get
      ()
      ()
      When p = 1, (B.2) are equivalent to (B.1), thus it holds the following:
      ()
      Expanding φ(t; p) and ψ(t; p) in Taylor series with respect to the embedding parameter p, we have
      ()
      where
      ()
      and will be determined later. Note that the above series contains the convergence control parameter h. Assuming that h is chosen so properly that the above series is convergent at p = 1, we have the solution series as follows:
      ()
      where
      ()
      Equating the like coefficients of the like powers of p we have
      ()
      and so on. Solving (B.13) using the initial condition (B.3) and (B.4), we obtain the following result:
      ()
      ()
      Adding (B.6), (B.14), (B.7), and (B.15), we get (4) and (5) in the text. Here we can obtain the solution of the equation using only two iterations which leads to the high accuracy.

        The full text of this article hosted at iucr.org is unavailable due to technical difficulties.