Volume 2013, Issue 1 120849

Research Article

Open Access

Combined Heat and Power Dynamic Economic Dispatch with Emission Limitations Using Hybrid DE-SQP Method

Corresponding Author

A. M. Elaiw

[email protected]

Department of Mathematics, Faculty of Science, King Abdulaziz University, P.O. Box 80203, Jeddah 21589, Saudi Arabia kau.edu.sa

Department of Mathematics, Faculty of Science, Al-Azhar University, Assiut 71511, Egypt azhar.edu.eg

Search for more papers by this author

X. Xia,

X. Xia

Centre of New Energy Systems, Department of Electrical, Electronic and Computer Engineering, University of Pretoria, Pretoria 0002, South Africa up.ac.za

Search for more papers by this author

A. M. Shehata,

A. M. Shehata

Department of Mathematics, Faculty of Science, Al-Azhar University, Assiut 71511, Egypt azhar.edu.eg

Search for more papers by this author

A. M. Elaiw,

Corresponding Author

A. M. Elaiw

[email protected]

Department of Mathematics, Faculty of Science, King Abdulaziz University, P.O. Box 80203, Jeddah 21589, Saudi Arabia kau.edu.sa

Department of Mathematics, Faculty of Science, Al-Azhar University, Assiut 71511, Egypt azhar.edu.eg

Search for more papers by this author

X. Xia,

X. Xia

Centre of New Energy Systems, Department of Electrical, Electronic and Computer Engineering, University of Pretoria, Pretoria 0002, South Africa up.ac.za

Search for more papers by this author

A. M. Shehata,

A. M. Shehata

Department of Mathematics, Faculty of Science, Al-Azhar University, Assiut 71511, Egypt azhar.edu.eg

Search for more papers by this author

First published: 13 November 2013

https://doi.org/10.1155/2013/120849

Citations: 15

Academic Editor: Jinde Cao

Share a link

Email
Wechat
Bluesky

Abstract

Combined heat and power dynamic economic emission dispatch (CHPDEED) problem is a complicated nonlinear constrained multiobjective optimization problem with nonconvex characteristics. CHPDEED determines the optimal heat and power schedule of committed generating units by minimizing both fuel cost and emission simultaneously under ramp rate constraints and other constraints. This paper proposes hybrid differential evolution (DE) and sequential quadratic programming (SQP) to solve the CHPDEED problem with nonsmooth and nonconvex cost function due to valve point effects. DE is used as a global optimizer, and SQP is used as a fine tuning to determine the optimal solution at the final. The proposed hybrid DE-SQP method has been tested and compared to demonstrate its effectiveness.

1. Introduction

Recently, combined heat and power (CHP) units, known as cogeneration or distributed generation, have played an increasingly important role in the utility industry. CHP units can provide not only electrical power but also heat to the customers. While the efficiency of the normal power generation is between 50% and 60%, the power and heat cogeneration increases the efficiency to around 90% [1]. Besides thier high efficiency, CHP units reduce the emission of gaseous pollutants (SO₂, NO_x, CO, and) by about 13–18% [2].

In order to utilize the integrated CHP system more CO₂ economically, combined heat and power economic dispatch (CHPED) problem is applied. The objective of the CHPED problem is to determine both power generation and heat production from units by minimizing the fuel cost such that both heat and power demands are met, while the combined heat and power units are operated in a bounded heat versus power plane. For most CHP units the heat production capacities depend on the power generation. This mutual dependency of the CHP units introduces a complication to the problem [3]. In addition, considering valve point effects in the CHPED problem makes the problem nonsmooth with multiple local optimal point which makes finding the global optimal challenging.

In the literature, several optimization techniques have been used to solve the CHPED problem with complex objective functions or constraints such as Lagrangian relaxation (LR) [4, 5], semidefinite programming (SDP) [6], augmented Lagrange combined with Hopfield neural network [7], harmony search (HS) algorithm [1, 8], genetic algorithm (GA) [9], ant colony search algorithm (ACSA) [10], mesh adaptive direct search (MADS) algorithm [11], self adaptive real-coded genetic algorithm (SARGA) [3], particle swarm optimization (PSO) [2, 12], artificial immune system (AIS) [13], bee colony optimization (BCO) [14], differential evolution [15], and evolutionary programming (EP) [16]. In [2, 13–15], the valve point effects and the transmission line losses are incorporated into the CHPED problem.

In the CHPED formulation the ramp rate limits of the units are neglected. Plant operators, to avoid life-shortening of the turbines and boilers, try to keep thermal stress on the equipments within the safe limits. This mechanical constraint is usually transformed into a limit on the rate of change of the electrical output of generators. Such ramp rate constraints link the generator operation in two consecutive time intervals. Combined heat and power dynamic economic dispatch (CHPDED) problem is an extension of CHPED problem where the ramp rate constraint is considered. The primary objective of the CHPDED problem is to determine the heat and power schedule of the committed units so as to meet the predicted heat and electricity load demands over a time horizon at minimum operating cost under ramp rate constraints and other constraints [17]. Since the ramp rate constraints couple the time intervals, the CHPDED problem is a difficult optimization problem. If the ramp rate constraints are not included in the optimization problem, the CHPDED problem is reduced to a set of uncoupled CHPED problems that can easily be solved. In the literature an overwhelming number of reported works deal with CHPED problem; however, the CHPDED problem has only been considered in [17].

The traditional dynamic economic dispatch (DED) problem which considers only thermal units that provide only electric power has been studied by several authors (see the review paper [18]). The emission has been taken into the traditional (DED) formulation in three main approaches. The first approach is to minimize the fuel cost and treat the emission as a constraint with a permissible limit (see, e.g., [19–21]). This formulation, however, has a severe difficulty in getting the trade-off relations between cost and emission [22]. The second approach handles both fuel cost and emission simultaneously as competing objectives [23–25]. The third approach treats the emission as another objective in addition to fuel cost objective. However, the multiobjective optimization problem is converted to a single-objective optimization problem by linear combination of both objectives [19, 26–30]. In the second and third approaches, the dynamic dispatch problem is referred to as dynamic economic emission dispatch (DEED) which is a multiobjective optimization problem, which minimizes both fuel cost and emission simultaneously under ramp rate constraint and other constraints [19, 24]. In this paper, we incoroporate the CHP units into the DEED problem. Combined heat and power dynamic economic emission dispatch (CHPDEED) is formulated with the objective to determine the unit power and heat production so that the system’s production cost and emission are simultaneously minimized, while the power and heat demands and other constraints are met [17]. The emission has been taken into consideration in the CHPED and CHPDED in [17, 31], respectively. In [17], both fuel cost and emission are simultaneously handled as competing objectives and the multiobjective problem is solved using an enhanced firefly algorithm (FA). In the present paper, the multiobjective optimization problem is converted into a single-objective optimization using the weighting method. This approach yields meaningful result to the decision maker when solved many times for different values of the weighting factor. In [17], the simulation results for test system are shown, but the data of the heat demand is not explicitly tabulated; instead it is expressed graphically (see Figure 12 in [17]). In this case a comparison of our proposed method and FA cannot be performed. In our paper, all the data and the solutions of the test system are available for comparison.

Differential evolution algorithm (DE), which was proposed by Storn and Price [32] is a population based stochastic parallel search technique. DE uses a rather greedy and less stochastic approach to problem solving compared to other evolutionary algorithms. DE has the ability to handle optimization problems with nonsmooth/nonconvex objective functions [32]. Moreover, it has a simple structure and a good convergence property, and it requires a few robust control parameters [32]. DE has been applied to the CHPED and CHPDED problems with non-smooth and non-convex cost functions in [15, 33], respectively.

The DE shares many similarities with evolutionary computation techniques such as genetic algorithms (GA) techniques. The system is initialized with a population of random solutions and searches for optima by updating generations. DE has evolution operators such as crossover and mutation. Although DE seem to be good methods to solve the CHPDEED problem with non-smooth and non-convex cost functions, solutions obtained are just near global optimum with long computation time. Therefore, hybrid methods such as DE-SQP can be effective in solving the CHPDEED problems with valve point effects.

The main contributions of the paper are as follows. (1) A multi-objective optimization problem is formulated using CHPDEED approach. The multi-objective optimization problem is converted into a single-objective optimization using the weighting method. (2) Hybrid DE-SQP method is proposed and validated for solving the CHPDEED problem with nonsmooth and nonconvex objective function. DE is used as a base level search for global exploration and SQP is used as a local search to fine-tune the solution obtained from DE. (3) The effectiveness of the proposed method is shown for test systems.

2. Problem Formulation

In this section we formulate the CHPDEED problem. The system under consideration has three types of generating units, conventional thermal units (TU), CHP units, and heat-only units (H). The power is generated by conventional thermal units and CHP units, while the heat is generated by CHP units and heat-only units. The objective of the CHPDEED problem is to simultaneously minimize the system’s production cost and emission so as to meet the predicted heat and power load demands over a time horizon under ramp rate and other constraints. The following objectives and constraints are taken into account in the formulation of the CHPDEED problem.

2.1. Objective Functions

In this section, we introduce the cost and emission functions of three types of generating units, conventional thermal units which produce power only, CHP units which produce both heat and power, and heat-only units which produce heat only.

2.1.1. Conventional Thermal Units

Cost. The cost function curve of a conventional thermal unit can be approximated by a quadratic function [35]. Power plants commonly have multiple valves which are used to control the power output of the unit. When steam admission valves in conventional thermal units are first open, a sudden increase in losses is registered which results in ripples in the cost function [18, 36]. This phenomenon is called as valve-point effects. The generator with valve-point effects has very different input-output curve compared with smooth cost function. Taking the valve-point effects into consideration, the fuel cost is expressed as the sum of a quadratic and sinusoidal functions [17, 24, 25, 37]. Therefore, the fuel cost function of the conventional thermal units is given by

()

where a_i, b_i, and c_i are positive constants, e_i and f_i are the coefficients of conventional thermal unit i reflecting valve-point effects,

is the power generation of conventional thermal unit i during the tth time interval [t − 1, t),

is the minimum capacity of conventional thermal unit i, and

is the fuel cost of conventional thermal unit i to produce

Emission. The amount of emission of gaseous pollutants from conventional thermal units can be expressed as a combination of quadratic function and exponential function of the unit’s active power output [21]. The emission function is given by

()

where

is the amount of emission from unit i from producing power

. Constants α_i, β_i, γ_i, η_i, and δ_i are the coefficients of the ith unit emission characteristics [24].

2.1.2. CHP Units

Cost. A CHP unit has a convex cost function in both power and heat. The form of the fuel cost function of CHP units can be given by [6, 17] the following:

()

where

is the generation fuel cost of CHP unit i to produce power

and heat

. Constants

, and

are the fuel cost coefficients of CHP unit j.

Emission. The emission of gaseous pollutants from CHP units is proportional to their active power output [17, 31]:

()

where

and

are the emission coefficients of CHP unit j.

2.1.3. Heat-Only Units

Cost. The cost function of heat-only units can take the following form [6, 17]:

()

where

, and

are the fuel cost coefficients of heat-only unit k and they are constants.

Emission. The emission of gaseous pollutants from CHP units is proportional to their heat output [17, 31]:

()

where

and

are the emission coefficients of heat-only unit k.

Let N be the number of dispatch intervals and N_p + N_c + N_h the number of committed units, where N_p is the number of conventional thermal units, N_c is the number of the CHP units, and N_h is the number of the heat-only units. Then the total fuel cost and amount of emission over the dispatch period [0, N] are given, respectively, by

()

where

, and

2.2. Constraints

There are three kinds of constraints considered in the CHPDEED problem, that is, the equilibrium constraints of power and heat production, the capacity limits of each unit, and the ramp rate limits.

(i) Power Production and Demand Balance

()

where P_D,t and Loss_t are the system power demand and transmission line losses at time t (i.e., the tth time interval), respectively. The B-coefficient method is one of the most commonly used by power utility industry to calculate the network losses. In this method the network losses are expressed as a quadratic function of the unit’s power outputs that can be approximated in the following:

()

where

()

and B_ij is the ijth element of the loss coefficient square matrix of size N_p + N_c.

(ii) Heat Production and Demand Balance

()

where H_D,t is the system heat demand at time t.

(iii) Capacity Limits of Conventional Thermal Units

()

where

and

are the minimum and maximum power capacity of conventional thermal unit i, respectively.

(iv) Capacity Limits of CHP Units

()

where

and

are the minimum and maximum power limit of CHP unit j, respectively, and they are functions of generated heat (

and

are the heat generation limits of CHP unit j which are functions of generated power

(v) Capacity Limits of Heat-Only Units

()

where

and

are the minimum and maximum heat capacity of heat-only unit k, respectively.

(vi) Upper/Down Ramp Rate Limits of Conventional Thermal Units

()

where

and

are the maximum ramp up/down rates for conventional thermal unit i [18].

(vii) Upper/Down Ramp Rate Limits of CHP Units

()

where

and

are the maximum ramp up/down rates for CHP unit j [17].

2.3. The Optimization Problem

Aggregating the objectives and constraints, the CHPDEED problem can be mathematically formulated as a nonlinear constrained multi-objective optimization problem which can be converted into a single-objective optimization using the weighting method as

()

where w ∈ [0,1] is a weighting factor. It will be noted that, when w = 1, problem (17) determines the optimal amount of the generated heat and power by minimizing the fuel cost regardless of emission and the problem will be referred to as combined heat and power dynamic economic dispatch (CHPDED) problem. If w = 0, then problem (17) determines the optimal amount of the generated power by minimizing the emission regardless of cost and the problem will be referred to as combined heat and power pure dynamic emission dispatch (CHPPDED).

3. Differential Evolution Method

DE is a simple yet powerful heuristic method for solving nonlinear, nonconvex, and nonsmooth optimization problems. DE algorithm is a population based algorithm using three operators; mutation, crossover, and selection to evolve from randomly generated initial population to final individual solution [32]. In the initialization a population of NP target vectors (parents) X_i = {x_1i, x_2i, …, x_Di}, i = 1,2, …, NP, is randomly generated within user-defined bounds, where D is the dimension of the optimization problem. Let

be the individual i at the current generation G. A mutant vector

is generated according to

()

with randomly chosen integer indexes r₁, r₂, r₃ ∈ {1,2, …, NP}. Here ℱ is the mutation factor.

According to the target vector

and the mutant vector

, a new trial vector (offspring)

is created with

()

where j = 1,2, …, D, i = 1,2, …, NP and rand(j) is the jth evaluation of a uniform random number between [0,1]. CR ∈ [0,1] is the crossover constant which has to be determined by the user. rnb(i) is a randomly chosen index from 1,2, …, D which ensures that

gets at least one parameter from

[32].

The selection process determines which of the vectors will be chosen for the next generation by implementing one-to-one competition between the offsprings and their corresponding parents. If f denotes the function to be minimized, then

()

where i = 1,2, …, NP. The value of f of each trial vector

is compared with that of its parent target vector

. The above iteration process of reproduction and selection will continue until a user-specified stopping criteria is met.

In this paper, we define the evaluation function for evaluating the fitness of each individual in the population in DE algorithm as follows:

()

where λ₁ and λ₂ are penalty values. Then the objective is to find f_min, the minimum evaluation value of all the individuals in all iterations. The penalty term reflects the violation of the equality constraints. Once the minimum of f is reached, the equality constraints are satisfied.

4. Sequential Quadratic Programming Method

SQP method can be considered as one of the best nonlinear programming methods for constrained optimization problems [38]. It outperforms every other nonlinear programming method in terms of efficiency, accuracy, and percentage of successful solutions over a large number of test problems. The method closely resembles Newton’s method for constrained optimization, just as is done for unconstrained optimization. At each iteration, an approximation is made of the Hessian of the Lagrangian function using Broyden-Fletcher-Goldfarb-Shanno (BFGS) quasi-Newton updating method. The result of the approximation is then used to generate a quadratic programming (QP) subproblem whose solution is used to form a search direction for a line search procedure. Since the objective function of the CHPDEED problem is non-convex and non-smooth, SQP ensures a local minimum for an initial solution. In this paper, DE is used as a global search and finally the best solution obtained from DE is given as initial condition for SQP method as a local search to fine-tune the solution. SQP simulations can be computed by the fmincon code of the MATLAB Optimization Toolbox.

5. Simulation Results

In this section we present two examples. The first example shows the efficiency of the proposed DE-SQP method for the DED problem. In the second example, the hybrid DE-SQP method is applied to the CHPDEED problem. In DE-SQP method, the control parameters are chosen as NP = 80, ℱ = 0.423 and CR = 0.885. The maximum number of iterations are selected as 20,000. The results represent the average of 30 runs of the proposed method. All computations are carried out by MATLAB program.

Example 1. This example consists of ten conventional thermal units to investigate the effectiveness of the proposed DE-SQP technique in solving the DED problem with valve point effects and transmission line losses. The technical data of the units as well as the demand for the 10-unit system are taken from [24]. The best solution of the DED problem is given in Table 1. Comparison between our proposed method (DE-SQP) and other methods is given in Table 2. It is observed that the proposed method reduces the total generation cost better than the other methods reported in the literature.

Table 1. Hourly generation (MW) schedule obtained from DED using DE-SQP for 10-unit system.

H											Loss
1	150.0000	135.0000	73.0000	70.3333	222.9974	155.1682	99.2918	120.0000	20.0000	10.0000	19.7912
2	150.0000	135.0000	101.9485	120.3333	222.6154	123.7029	129.2918	90.0000	48.7980	10.7150	22.4058
3	150.0000	135.0000	181.9485	170.3333	174.2621	130.9190	129.6896	120.0000	53.5785	40.7150	28.4468
4	150.0000	135.0000	183.1516	218.2899	223.5485	160.0000	129.3947	120.0000	80.0000	42.0564	35.4415
5	150.0000	135.0000	258.8414	249.7412	224.0147	160.0000	128.5373	120.0000	80.0000	13.2136	39.3484
6	150.0000	135.0000	315.1962	299.7412	243.0000	160.0000	129.8624	120.0000	80.0000	43.2136	48.0136
7	150.0000	176.9470	340.0000	300.0000	243.0000	160.0000	130.0000	120.0000	80.0000	55.0000	52.9470
8	178.2448	228.3049	340.0000	300.0000	243.0000	160.0000	129.9436	120.0000	80.0000	54.9118	58.4054
9	258.2448	308.3049	340.0000	300.0000	243.0000	160.0000	130.0000	120.0000	80.0000	55.0000	70.5500
10	289.0490	384.5331	340.0000	300.0000	243.0000	160.0000	130.0000	120.0000	80.0000	55.0000	79.5821
11	368.7363	397.1230	340.0000	300.0000	243.0000	160.0000	130.0000	120.0000	80.0000	55.0000	87.8595
12	374.8564	439.5807	340.0000	300.0000	243.0000	160.0000	130.0000	120.0000	80.0000	55.0000	92.4378
13	342.1737	386.2429	340.0000	300.0000	243.0000	160.0000	130.0000	120.0000	80.0000	55.0000	84.4166
14	262.1737	306.2429	340.0000	300.0000	243.0000	160.0000	130.0000	120.0000	80.0000	53.1527	70.5693
15	182.1737	226.2429	340.0000	299.9639	243.0000	160.0000	130.0000	120.0000	80.0000	53.0342	58.4148
16	150.0000	146.2429	294.7660	249.9639	223.6700	160.0000	129.6353	120.0000	80.0000	43.3613	43.6398
17	150.0000	135.0000	258.1720	249.5279	223.9121	160.0000	128.8682	120.0000	80.0000	13.8650	39.3459
18	150.0000	151.6366	298.4749	299.5279	243.0000	160.0000	129.7933	120.0000	80.0000	43.6183	48.0511
19	227.2425	231.6366	299.3393	300.0000	243.0000	160.0000	130.0000	120.0000	80.0000	43.5728	58.7914
20	307.2425	311.6366	340.0000	300.0000	243.0000	160.0000	130.0000	120.0000	80.0000	55.0000	74.8793
21	265.4293	301.1183	340.0000	300.0000	243.0000	160.0000	130.0000	120.0000	80.0000	55.0000	70.5476
22	185.4293	221.1183	263.3759	250.0000	225.8767	160.0000	129.8685	120.0000	80.0000	41.1109	48.7801
23	150.0000	141.1183	183.3759	200.0000	223.4887	155.9437	128.7427	120.0000	50.0000	11.1109	31.7806
24	150.0000	135.0000	173.1056	180.5739	173.7249	118.1382	128.6826	120.0000	20.0000	10.0000	25.2260

Table 2. Comparison results of 10-thermal-unit system (cost × 10⁶ $) for the DED problem.

Method	EP [34]	PSO [34]	AIS [34]	NSGA-II [24]	IBFA [30]	DE-SQP
cost ($)	2.5854	2.5722	2.5197	2.5168	2.4817	2.4659

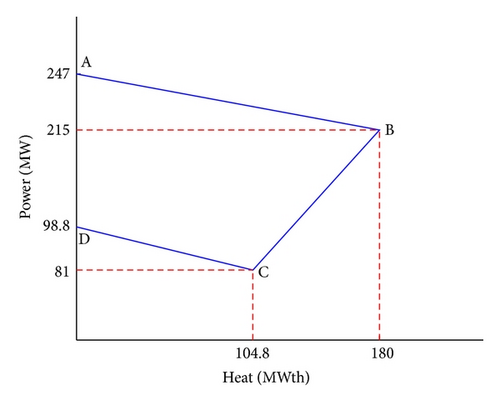
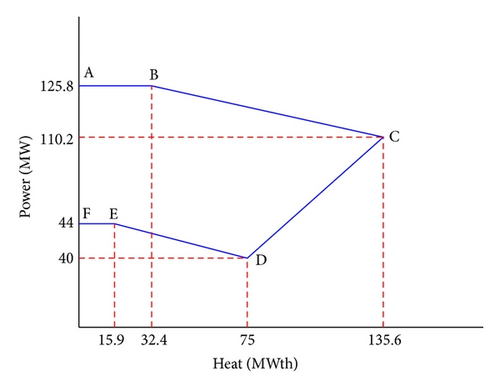
Example 2. This example is 11-unit system (eight conventional thermal units, two CHP units, and one heat-only unit) for solving the CHPDED, CHPDEED, and CHPPDED problems using DE-SQP method. We shall solve the CHPDEED problem when w = 0.5, in addition to the CHPDED and CHPPDED problems which correspond to w = 1 and w = 0, respectively. The technical data of conventional thermal units, the matrix B, and the demand are taken from the 10-unit system presented in [24]. The 5th and 8th conventional units in [24] were replaced by two CHP units. The technical data of the two CHP units and the heat-only unit are taken from [17] and are given in Table 3. The heat demand for 24 hours is given in Table 4. The feasible operating regions of the two CHP units are given in Figures 1 and 2 (see [4, 14]).

Table 3. Data of the CHP units and heat-only unit system.

CHP units
j = 1	2650	14.5	0.0345	4.2	0.030	0.031	0.00015	0.0015	70
j = 2	1250	36	0.0435	0.6	0.027	0.011	0.00015	0.0015	50

Heat-only units

k = 1		2695.2	0	950	2.0109	0.038	0.0008	0.0010

Table 4. Heat load demand of the three-unit system for 24 hours.

Time (h)	Demand (MWth)
1	390
2	400
3	410
4	420
5	440
6	450
7	450
8	455
9	460
10	460
11	470
12	480
13	470
14	460
15	450
16	450
17	420
18	435
19	445
20	450
21	445
22	435
23	400
24	400

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Heat-power feasible operating region for CHP unit 1.

The best solutions of the CHPDED, CHPDEED, and CHPPDED problems for DE-SQP algorithm are given in Tables 5, 6, and 7, respectively. The best cost, the amount of emission, and the transmission line losses are also given in Tables 5–7. It is seen that the cost is 2.5257 × 10⁶ $ under CHPDED, but it increases to 2.6945 × 10⁶ $ under CHPPDED. The emission obtained from CHPDED is 2.8287 × 10⁵ lb, but it decreases to 2.4195 × 10⁵ lb under CHPPDED. Under the CHPDEED problem, the cost is 2.5295 × 10⁶ $ which is more than 2.5257 × 10⁶ $ and less than 2.6945 × 10⁶ $. Moreover, the emission is 2.7209 × 10⁵ lb which is less than 2.8287 × 10⁵ lb and more than 2.4195 × 10⁵ lb.

Table 5. Hourly heat and power schedule obtained from CHPDED.

H											Loss
1	150.0000	135.0000	74.5372	72.0784	124.5129	124.4302	20.0000	10.0000	236.8041	110.1974	21.5630	57.3450	135.5994	197.0556
2	150.0000	135.0000	98.1135	122.0784	122.2113	101.6179	48.2025	10.0000	236.8011	110.1974	24.2248	57.3614	135.5994	207.0392
3	150.0000	135.0000	178.1135	172.0784	120.7640	98.7468	78.2025	10.0000	235.3275	110.1974	30.4319	65.6496	135.5994	208.7509
4	150.0000	135.0000	188.0106	218.5077	160.0000	126.3142	80.0000	40.0000	235.2182	110.1974	37.2496	66.2643	135.5994	218.1363
5	150.0000	135.0000	268.0106	244.7145	128.0292	129.9179	80.0000	42.2707	233.2313	110.1974	41.3736	77.4390	135.5994	226.9616
6	150.0000	135.0000	334.4706	294.7145	160.0000	130.0000	80.0000	48.0931	235.6609	110.1974	50.1383	63.7746	135.5994	250.6260
7	150.0000	199.1593	340.0000	300.0000	160.0000	130.0000	80.0000	49.7990	238.0991	110.1974	55.2549	50.0614	135.5994	264.3392
8	189.7336	229.5497	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	242.2569	110.1974	60.7377	26.6766	135.5994	292.7240
9	265.3596	309.5497	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	247.0000	110.1974	73.1068	0.0	135.5994	324.4006
10	303.6024	378.5162	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	246.9410	110.1974	82.2580	0.3317	135.5994	324.0689
11	368.8317	405.6648	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	247.0000	110.1974	90.6945	0.0	135.5994	334.4006
12	367.7179	455.4472	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	247.0000	110.1974	95.3624	0.0	135.5994	344.4006
13	352.0071	385.0034	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	247.0000	110.1974	87.2079	0.0	135.5994	334.4006
14	272.0071	305.0034	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	244.9090	110.1974	73.1169	11.7604	135.5994	312.6402
15	193.6233	225.0034	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	242.9121	110.1974	60.7362	22.9917	135.5994	291.4089
16	150.0000	145.0034	296.8330	250.8703	160.0000	129.9573	80.0000	43.4626	233.2660	110.1974	45.5900	77.2439	135.5994	237.1567
17	150.0000	135.0000	260.0109	250.0000	160.0000	100.0000	80.0000	40.9143	235.3888	110.1974	41.5121	65.3046	135.5994	219.0959
18	150.0000	151.0646	319.4485	300.0000	160.0000	130.0000	80.0000	40.0577	237.4722	110.1974	50.2419	53.5869	135.5994	245.8137
19	229.4141	231.0646	313.3779	300.0000	160.0000	130.0000	80.0000	46.0360	237.0065	110.1974	61.0988	56.2062	135.5994	253.1943
20	309.4141	311.0646	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	247.0000	116.9757	77.4552	0.0	90.7694	359.2306
21	272.4577	300.8037	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	247.0000	111.8344	73.0959	0.0	124.7723	320.2277
22	192.4577	220.8037	260.6669	250.0000	160.0000	124.1397	80.0000	45.9763	234.6724	110.1974	50.9154	69.3338	135.5994	230.0668
23	150.0000	140.8037	180.6669	200.0000	127.6584	130.0000	50.0000	40.0000	236.4213	110.1974	33.7482	59.4980	135.5994	204.9026
24	150.0000	135.0000	100.6669	177.0362	123.2649	128.6636	42.3316	10.0000	234.6572	109.5624	27.1834	69.4196	135.0513	195.5291

Cost ($) = 2.5257 × 10⁶. Emission (lb) = 2.8287 × 10⁵. Total loss (MW) = 1.3443 × 10³.

Table 6. Hourly heat and power schedule obtained from CHPDEED (w = 0.5).

t											Loss
1	150.0000	135.0000	77.5875	65.0188	122.5177	129.0996	20.0000	10.0000	238.1722	110.1974	21.5935	49.6499	135.5994	204.7506
2	150.0000	135.0000	73.0000	115.0188	123.4971	126.6027	50.0000	13.3209	237.5744	110.1974	24.2115	53.0122	135.5994	211.3884
3	150.0000	135.0000	135.6390	143.2389	123.5028	130.0000	80.0000	43.3209	237.2689	110.1974	30.1680	54.7308	135.5994	219.6698
4	150.0000	135.0000	197.2495	193.2389	160.0000	130.0000	80.0000	46.3828	241.1942	110.1974	37.2630	32.6533	135.5994	251.7473
5	150.0000	135.0000	227.7945	243.2389	160.0000	130.0000	80.0000	46.9362	238.0276	110.1974	41.1946	50.4634	135.5994	253.9371
6	150.0000	148.0006	307.4622	293.2389	160.0000	130.0000	80.0000	55.0000	244.2131	110.1974	50.1122	15.6745	135.5994	298.7261
7	153.7715	216.0682	309.3974	300.0000	160.0000	130.0000	80.0000	55.0000	242.8740	110.1974	55.3090	23.2061	135.5994	291.1945
8	204.6091	224.9723	327.2185	300.0000	160.0000	130.0000	80.0000	55.0000	244.8130	110.1974	60.8102	12.3003	135.5994	307.1003
9	269.9376	304.9723	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	247.0000	110.1974	73.1072	0.0	135.5994	324.4006
10	302.8816	379.1708	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	247.0000	110.2066	82.2590	0.0	135.5384	324.4616
11	374.8455	398.1777	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	247.0000	111.6628	90.6861	0.0	125.9076	344.0924
12	396.3649	416.9874	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	247.0000	119.8750	95.2273	0.0	71.5941	408.4059
13	353.1036	382.7187	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	247.0000	111.3732	87.1956	0.0	127.8228	342.1772
14	273.1036	302.7187	339.8378	300.0000	160.0000	130.0000	80.0000	55.0000	246.2562	110.1974	73.1138	4.1831	135.5994	320.2175
15	213.0095	222.7187	321.3321	300.0000	160.0000	130.0000	80.0000	55.0000	244.5974	110.1974	60.8552	13.5127	135.5994	300.8879
16	150.0000	142.7187	291.8181	250.0000	160.0000	130.0000	80.0000	46.1485	238.7061	110.1974	45.5889	46.6476	135.5994	267.7530
17	150.0000	135.0000	228.5656	240.9760	160.0000	130.0000	80.0000	45.7659	240.7225	110.1974	41.2275	35.3065	135.5994	249.0941
18	150.0000	207.5152	294.3486	250.0000	160.0000	130.0000	80.0000	55.0000	241.3976	110.1974	50.4588	31.5093	135.5994	267.8913
19	227.0251	235.5649	297.1019	300.0000	160.0000	130.0000	80.0000	55.0000	242.1587	110.1974	61.0481	27.2289	135.5994	282.1716
20	307.0251	315.5649	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	247.0000	114.8749	77.4649	0.00	104.6636	345.3364
21	270.9950	301.2766	340.0000	300.0000	160.0000	130.0000	80.0000	55.0000	247.0000	112.8155	73.0871	0.00	118.2834	326.7166
22	190.9950	221.2766	260.0000	250.0000	157.3134	126.2505	80.0000	43.7439	239.1773	110.1974	50.9541	43.9973	135.5994	255.4033
23	150.0000	141.2766	180.0000	200.0000	154.2635	126.4607	51.1156	13.7439	238.8386	110.1974	33.8966	45.9019	135.5994	218.4987
24	150.0000	135.0000	100.0000	150.0000	118.3525	129.7054	78.8178	10.0000	235.4040	103.7586	27.0385	65.2191	130.0411	204.7398

Cost ($) = 2.5295 × 10⁶. Emission (lb) = 2.7209 × 10⁵. Total loss (MW) = 1.3439 × 10³.

Table 7. Hourly heat and power schedule obtained from CHPPDED.

H											Loss
1	150.0000	135.0000	73.0000	60.0000	84.3406	63.6438	64.0384	55	247	125.8	21.8228	0.0	31.4722	358.5278
2	150.0000	135.0000	75.2831	75.5559	107.4058	83.4606	80.0000	55	247	125.8	24.5054	0.0	32.4074	367.5926
3	150.0000	146.7217	108.1787	108.2058	154.2362	113.4606	80.0000	55	247	125.8	30.6030	0.0	18.2661	391.7339
4	187.3290	187.7229	135.7677	135.7127	160.0000	130.0000	80.0000	55	247	125.8	38.3323	0.0	32.4074	387.5926
5	209.9448	210.5929	152.0706	152.2866	160.0000	130.0000	80.0000	55	247	125.8	42.6949	0.0	32.4074	407.5926
6	252.6588	252.9491	188.3610	188.4287	160.0000	130.0000	80.0000	55	247	125.8	52.1977	0.0	25.5244	424.4756
7	272.2261	272.7171	208.2382	208.3486	160.0000	130.0000	80.0000	55	247	125.8	57.3300	0.0	26.7637	423.2363
8	290.5854	291.0583	229.5277	229.7367	160.0000	130.0000	80.0000	55	247	125.8	62.7082	0.0	32.4074	422.5926
9	323.8400	324.1415	276.1324	276.3023	160.0000	130.0000	80.0000	55	247	125.8	74.2162	0.0	25.5487	434.4513
10	346.7105	346.8973	313.1106	300.0000	160.0000	130.0000	80.0000	55	247	125.8	82.5184	0.0	32.4074	427.5926
11	379.2210	379.5185	340.0000	300.0000	160.0000	130.0000	80.0000	55	247	125.8	90.5395	0.0	29.4012	440.5988
12	403.5504	403.8291	340.0000	300.0000	160.0000	130.0000	80.0000	55	247	125.8	95.1796	0.0	31.9845	448.0155
13	361.7512	362.0812	337.4700	300.0000	160.0000	130.0000	80.0000	55	247	125.8	87.1023	0.0	32.0189	437.9811
14	323.7805	324.1252	276.7607	275.7492	160.0000	130.0000	80.0000	55	247	125.8	74.2157	0.0	25.5863	434.4137
15	291.7264	292.3796	231.0966	225.7492	160.0000	130.0000	80.0000	55	247	125.8	62.7519	0.0	31.8710	418.1290
16	229.7976	230.1379	167.7688	175.7492	160.0000	130.0000	80.0000	55	247	125.8	47.2535	0.0	31.3306	418.6694
17	210.0699	210.4074	152.1822	152.2351	160.0000	130.0000	80.0000	55	247	125.8	42.6946	0.0	32.3578	387.6422
18	252.7542	253.2318	188.2091	188.2081	160.0000	130.0000	80.0000	55	247	125.8	52.2031	0.0	29.7791	405.2209
19	288.2429	288.7410	226.6332	237.2113	160.0000	130.0000	80.0000	55	247	125.8	62.6285	0.0	27.4724	417.5276
20	335.1319	335.4397	294.6392	287.2113	160.0000	130.0000	80.0000	55	247	125.8	78.2222	0.0	31.3390	418.6610
21	332.6192	333.0535	282.3523	252.7233	160.0000	130.0000	80.0000	55	247	125.8	74.5483	0.0	32.3100	412.6900
22	252.6192	253.0535	202.3523	202.7233	149.4115	112.3565	80.0000	55	247	125.8	52.3163	0.0	27.3503	407.6497
23	172.6192	173.0535	122.3523	152.7233	135.8629	102.0552	80.0000	55	247	125.8	34.4664	0.0	25.1547	374.8453
24	150.0000	135.0000	90.3380	102.7233	128.7354	96.7805	80.0000	55	247	125.8	27.3771	0..0	31.5331	368.4669

Cost ($) = 2.6945 × 10⁶. Emission (lb) = 2.4195 × 10⁵. Total loss (MW) = 1.3684 × 10³.

6. Conclusion

This paper presents a hybrid method combining differential evolution (DE) and sequential quadratic programming (SQP) for solving dynamic dispatch (CHPDED, CHPDEED, and CHPPDED) problems with valve-point effects including generator ramp rate limits. In this paper, DE is first applied to find the best solution. This best solution is given to SQP as an initial condition that fine tunes the optimal solution at the final. The feasibility and efficiency of the DE-SQP were illustrated by conducting case studies with system consisting of eight conventional thermal units, two CHP units, and one heat-only unit.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

This work was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under Grant no. (130-107-D1434). The authors, therefore, acknowledge with thanks DSR technical and financial support.

References

1 Vasebi A., Fesanghary M., and Bathaee S. M. T., Combined heat and power economic dispatch by harmony search algorithm, International Journal of Electrical Power and Energy Systems. (2007) 29, no. 10, 713–719, 2-s2.0-35748944145, https://doi.org/10.1016/j.ijepes.2007.06.006.
10.1016/j.ijepes.2007.06.006
Web of Science® Google Scholar
2 Behnam M., Mohammad M., and Abbas R., Combined heat and power economic dispatch problem solution using particle swarm optimization with time varying acceleration coefficients, Electric Power Systems Research. (2013) 95, 9–18.
10.1016/j.epsr.2012.08.005
Web of Science® Google Scholar
3 Subbaraj P., Rengaraj R., and Salivahanan S., Enhancement of combined heat and power economic dispatch using self adaptive real-coded genetic algorithm, Applied Energy. (2009) 86, no. 6, 915–921, 2-s2.0-60949084539, https://doi.org/10.1016/j.apenergy.2008.10.002.
10.1016/j.apenergy.2008.10.002
Web of Science® Google Scholar
4 Guo T., Henwood M. I., and van Ooijen M., An algorithm for combined heat and power economic dispatch, IEEE Transactions on Power Systems. (1996) 11, no. 4, 1778–1784, 2-s2.0-0030285962, https://doi.org/10.1109/59.544642.
10.1109/59.544642
Web of Science® Google Scholar
5 Sashirekha A., Pasupuleti J., Moin N. H., and Tan C. S., Combined heat and power (CHP) economic dispatch solved using Lagrangian relaxation with surrogate subgradient multiplier updates, Electrical Power and Energy Systems. (2013) 44, 421–430.
10.1016/j.ijepes.2012.07.038
Web of Science® Google Scholar
6 Jubril A. M., Adediji A. O., and Olaniyan O. A., Solving the combined heat and power dispatch problem: a semi-definite programming approach, Electric Power Components and Systems. (2012) 40, 1362–1376.
10.1080/15325008.2012.694972
Web of Science® Google Scholar
7 Dieu V. N. and Ongsakul W., Augmented lagrangehopfield network for economic load dispatch with combined heat and power, Electric Power Components and Systems. (2009) 37, no. 12, 1289–1304, 2-s2.0-74949137682, https://doi.org/10.1080/15325000903054969.
10.1080/15325000903054969
Web of Science® Google Scholar
8 Khorram E. and Jaberipour M., Harmony search algorithm for solving combined heat and power economic dispatch problems, Energy Conversion and Management. (2011) 52, no. 2, 1550–1554, 2-s2.0-78649330861, https://doi.org/10.1016/j.enconman.2010.10.017.
10.1016/j.enconman.2010.10.017
Web of Science® Google Scholar
9 Su C. and Chiang C., An incorporated algorithm for combined heat and power economic dispatch, Electric Power Systems Research. (2004) 69, no. 2-3, 187–195, 2-s2.0-1342344960, https://doi.org/10.1016/j.epsr.2003.08.006.
10.1016/j.epsr.2003.08.006
Web of Science® Google Scholar
10 Song Y. H., Chou C. S., and Stonham T. J., Combined heat and power economic dispatch by improved ant colony search algorithm, Electric Power Systems Research. (1999) 52, no. 2, 115–121, 2-s2.0-0033363476, https://doi.org/10.1016/S0378-7796(99)00011-5.
10.1016/S0378-7796(99)00011-5
Web of Science® Google Scholar
11 Sadat Hosseini S. S., Jafarnejad A., Behrooz A. H., and Gandomi A. H., Combined heat and power economic dispatch by mesh adaptive direct search algorithm, Expert Systems with Applications. (2011) 38, no. 6, 6556–6564, 2-s2.0-79951579662, https://doi.org/10.1016/j.eswa.2010.11.083.
10.1016/j.eswa.2010.11.083
Web of Science® Google Scholar
12 Ramesh V., Jayabarathi T., Shrivastava N., and Baska A., A novel selective particle swarm optimization approach for combined heat and power economic dispatch, Electric Power Components and Systems. (2009) 37, no. 11, 1231–1240, 2-s2.0-74949117363, https://doi.org/10.1080/15325000902994348.
10.1080/15325000902994348
Web of Science® Google Scholar
13 Basu M., Artificial immune system for combined heat and power economic dispatch, Electrical Power and Energy Systems. (2012) 43, 1–5.
10.1016/j.ijepes.2012.05.016
Web of Science® Google Scholar
14 Basu M., Bee colony optimization for combined heat and power economic dispatch, Expert Systems with Applications. (2011) 38, no. 11, 13527–13531, 2-s2.0-80955180216, https://doi.org/10.1016/j.eswa.2011.03.067.
10.1016/j.eswa.2011.03.067
Web of Science® Google Scholar
15 Basu M., Combined heat and power economic dispatch by using differential evolution, Electric Power Components and Systems. (2010) 38, no. 8, 996–1004, 2-s2.0-77952996251, https://doi.org/10.1080/15325000903571574.
10.1080/15325000903571574
Web of Science® Google Scholar
16 Wong K. P. and Algie C., Evolutionary programming approach for combined heat and power dispatch, Electric Power Systems Research. (2002) 61, no. 3, 227–232, 2-s2.0-1642286903, https://doi.org/10.1016/S0378-7796(02)00028-7.
10.1016/S0378-7796(02)00028-7
Web of Science® Google Scholar
17 Taher N., Rasoul A. A., Alireza R., and Babak A., A new multi-objective reserve constrained combined heat and power dynamic economic emission dispatch, Energy. (2012) 42, 530–545.
10.1016/j.energy.2012.02.041
Web of Science® Google Scholar
18 Xia X. and Elaiw A. M., Optimal dynamic economic dispatch of generation: a review, Electric Power Systems Research. (2010) 80, no. 8, 975–986, 2-s2.0-79955980323, https://doi.org/10.1016/j.epsr.2009.12.012.
10.1016/j.epsr.2009.12.012
Web of Science® Google Scholar
19 Elaiw A. M., Xia X., and Shehata A. M., Application of model predictive control to optimal dynamic dispatch of generation with emission limitations, Electric Power Systems Research. (2012) 84, no. 1, 31–44, 2-s2.0-80054983560, https://doi.org/10.1016/j.epsr.2011.09.024.
10.1016/j.epsr.2011.09.024
Web of Science® Google Scholar
20 Granelli G. P., Montagna M., Pasini G. L., and Marannino P., Emission constrained dynamic dispatch, Electric Power Systems Research. (1992) 24, no. 1, 55–64, 2-s2.0-0026890278.
10.1016/0378-7796(92)90045-3
Web of Science® Google Scholar
21 Song Y. H. and Yu I., Dynamic load dispatch with voltage security and environmental constraints, Electric Power Systems Research. (1997) 43, no. 1, 53–60, 2-s2.0-0031257917.
10.1016/S0378-7796(97)01160-7
Web of Science® Google Scholar
22 Abido M. A., Environmental/economic power dispatch using multiobjective evolutionary algorithms, IEEE Transactions on Power Systems. (2003) 18, no. 4, 1529–1537, 2-s2.0-0344395549, https://doi.org/10.1109/TPWRS.2003.818693.
10.1109/TPWRS.2003.818693
Web of Science® Google Scholar
23 Basu M., Dynamic economic emission dispatch using evolutionary programming and fuzzy satisfied method, International Journal of Emerging Electric Power Systems. (2007) 8, 1–15.
10.2202/1553-779X.1146
Google Scholar
24 Basu M., Dynamic economic emission dispatch using nondominated sorting genetic algorithm-II, International Journal of Electrical Power and Energy Systems. (2008) 30, no. 2, 140–149, 2-s2.0-38749150018, https://doi.org/10.1016/j.ijepes.2007.06.009.
10.1016/j.ijepes.2007.06.009
Web of Science® Google Scholar
25 Guo C. X., Zhan J. P., and Wu Q. H., Dynamic economic emission dispatch based on group search optimizer with multiple producers, Electric Power Systems Research. (2012) 86, 8–16, 2-s2.0-84857050972, https://doi.org/10.1016/j.epsr.2011.11.015.
10.1016/j.epsr.2011.11.015
Web of Science® Google Scholar
26 Elaiw A. M., Xia X., and Shehata A. M., Hybrid DE-SQP and hybrid PSO-SQP methods for solving dynamic economic emission dispatch problem with valve-point effects, Electric Power Systems Research. (2013) 84, 192–200.
10.1016/j.epsr.2013.05.015
Google Scholar
27 Elaiw A. M., Xia X., and Shehata A. M., Minimization of fuel costs and gaseous emissions of electric power generation by model predictive control, Mathematical Problems in Engineering. (2013) 2013, 15, 906958, https://doi.org/10.1155/2013/906958, MR3044284.
10.1155/2013/906958
Web of Science® Google Scholar
28 Alsumait J. S., Qasem M., Sykulski J. K., and Al-Othman A. K., An improved Pattern Search based algorithm to solve the Dynamic Economic Dispatch problem with valve-point effect, Energy Conversion and Management. (2010) 51, no. 10, 2062–2067, 2-s2.0-77955317048, https://doi.org/10.1016/j.enconman.2010.02.039.
10.1016/j.enconman.2010.02.039
Web of Science® Google Scholar
29 Basu M., Particle swarm optimization based goal-attainment method for dynamic economic emission dispatch, Electric Power Components and Systems. (2006) 34, no. 9, 1015–1025, 2-s2.0-33745417056, https://doi.org/10.1080/15325000600596759.
10.1080/15325000600596759
Web of Science® Google Scholar
30 Nicole P., Anshul T., Shashikala T., and Manjaree P., An improved bacterial foraging algorithm for combined static/dynamic environmental economic dispatch, Applied Soft Computing. (2012) 12, 3500–3513.
10.1016/j.asoc.2012.06.011
Web of Science® Google Scholar
31 Piperagkas G. S., Anastasiadis A. G., and Hatziargyriou N. D., Stochastic PSO-based heat and power dispatch under environmental constraints incorporating CHP and wind power units, Electric Power Systems Research. (2011) 81, no. 1, 209–218, 2-s2.0-77958051126, https://doi.org/10.1016/j.epsr.2010.08.009.
10.1016/j.epsr.2010.08.009
Web of Science® Google Scholar
32 Storn R. and Price K., Differential Evolution—a simple and efficient adaptive scheme for global optimization over continuous spaces, Journal of Global Optimization. (1997) 11, no. 4, 341–359, https://doi.org/10.1023/A:1008202821328, MR1479553, ZBL0888.90135.
10.1023/A:1008202821328
Web of Science® Google Scholar
33 Elaiw A. M., Xia X., and Shehata A. M., Hybrid DE-SQP method for solving combined heat and power dynamic economic dispatch problem, Mathematical Problems in Engineering. (2013) 2013, 7, 982305, https://doi.org/10.1155/2013/982305.
10.1155/2013/982305
Web of Science® Google Scholar
34 Basu M., Artificial immune system for dynamic economic dispatch, International Journal of Electrical Power and Energy Systems. (2011) 33, no. 1, 131–136, 2-s2.0-77957575095, https://doi.org/10.1016/j.ijepes.2010.06.019.
10.1016/j.ijepes.2010.06.019
Web of Science® Google Scholar
35 Xia X., Zhang J., and Elaiw A., An application of model predictive control to the dynamic economic dispatch of power generation, Control Engineering Practice. (2011) 19, no. 6, 638–648, 2-s2.0-79955976135, https://doi.org/10.1016/j.conengprac.2011.03.001.
10.1016/j.conengprac.2011.03.001
Web of Science® Google Scholar
36 Panigrahi C. K., Chattopadhyay P. K., Chakrabarti R. N., and Basu M., Simulated annealing technique for dynamic economic dispatch, Electric Power Components and Systems. (2006) 34, no. 5, 577–586, 2-s2.0-33344461623, https://doi.org/10.1080/15325000500360843.
10.1080/15325000500360843
Web of Science® Google Scholar
37 Attaviriyanupap P., Kita H., Tanaka E., and Hasegawa J., A hybrid EP and SQP for dynamic economic dispatch with nonsmooth fuel cost function, IEEE Transactions on Power Systems. (2002) 17, no. 2, 411–416, 2-s2.0-0036577082, https://doi.org/10.1109/TPWRS.2002.1007911.
10.1109/TPWRS.2002.1007911
Web of Science® Google Scholar
38 Boggs P. T. and Tolle J. W., Sequential quadratic programming, Acta Numerica. (1995) 3, no. 4, 1–52.
10.1017/S0962492900002518
Google Scholar

Citing Literature

All articles

Combined Heat and Power Dynamic Economic Dispatch with Emission Limitations Using Hybrid DE-SQP Method

Abstract

1. Introduction