Volume 2013, Issue 1 120543

Research Article

Open Access

Robust H_∞ Switching Rule Design for Boost Converters with Uncertain Parameters and Disturbances

Yang Yang,

Yang Yang

School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China njust.edu.cn

Search for more papers by this author

Hamid Reza Karimi,

Hamid Reza Karimi

orcid.org/0000-0001-7629-3266

Department of Engineering, Faculty of Engineering and Science, University of Agder, 4898 Grimstad, Norway uia.no

Search for more papers by this author

Zhengrong Xiang,

Corresponding Author

Zhengrong Xiang

[email protected]

School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China njust.edu.cn

Search for more papers by this author

Yang Yang,

Yang Yang

School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China njust.edu.cn

Search for more papers by this author

Hamid Reza Karimi,

Hamid Reza Karimi

orcid.org/0000-0001-7629-3266

Department of Engineering, Faculty of Engineering and Science, University of Agder, 4898 Grimstad, Norway uia.no

Search for more papers by this author

Zhengrong Xiang,

Corresponding Author

Zhengrong Xiang

[email protected]

School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China njust.edu.cn

Search for more papers by this author

First published: 06 June 2013

https://doi.org/10.1155/2013/120543

Citations: 5

Academic Editor: Lixian Zhang

Share a link

Email
Wechat
Bluesky

Abstract

This paper is concerned with the design problem of robust H_∞ switching rule for Boost converters with uncertain parameters and disturbances. Firstly, the Boost converter is modeled as a switched affine linear system with uncertain parameters and disturbances. Then, using common Lyapunov function approach and linear matrix inequality (LMI) technique, a novel switching rule is proposed such that the H_∞ model reference tracking performance is satisfied. Finally, a simulation result is provided to show the validity of the proposed method.

1. Introduction

The last years have witnessed the crescent interest of the scientific community in the study of hybrid systems because of their wide applications in many fields, such as chemical processing, communication networks, traffic control, automotive engine control, and aircraft control [1–4]. The stochastic hybrid systems, also called Markov jump systems, represent an important class of hybrid systems that are popular in modeling many practical systems, such as manufacturing systems, power systems, aerospace systems, and networked control systems that may experience random abrupt changes in their structures and parameters [5–8]. Recently, the problem of the adaptive tracking for a class of stochastic nonlinear systems with stationary Markovian switching was considered in [9]. The problem of robust mode-dependent delayed state feedback H_∞ control for a class of uncertain time-delay systems with Markovian switching parameters and mixed discrete, neutral, and distributed delays was investigated in [10].

As a specific type of hybrid systems, switched systems have received a great attention in the last decades. Many examples of such systems can be found in real world, such as power electronics, networked control systems [11]. The switching rule design is one of the key issues in the study of switched systems. Based on the switching rule design, many important problems, such as stability, model reduction, H_∞ control or filtering problem, and tracking control, have been extensively investigated in [12–22]. For example, the problems of stability and stabilization of impulsive switched systems with time delays were considered in [12]. The problems of finite-time stability analysis and stabilization for switched nonlinear discrete-time systems were addressed in [13]. The model reduction of switched systems was investigated in [14, 15]. In [16–22], the H_∞ control and filtering problems of switched systems were studied. In [23], the tracking control for switched linear systems with time delay was investigated, and a tracking control law was designed such that the H_∞ model reference tracking performance is satisfied. There are also many papers discussing the switching rule design for switched affine systems; see, for instance, [24–26] and the references therein.

On the other hand, the switch-mode DC-DC converters are widely applied in DC motor drives and regulated DC power supplies where the object is to convert the unregulated DC input into a desired DC output voltage level [27]. Due to the fact that the DC-DC converters operate in a switch mode where an interaction between continuous and discrete dynamics exists, they can be modeled as hybrid systems. Recently, a unified method for fast modeling of DC-DC switching converters in the continuous conduction mode and discontinuous conduction mode was proposed in [28]. A tristate converter was modeled as a switched affine system, and a controller was designed to ensure that the corresponding closed-loop system is always stable in the safe set [29]. In [27], a hybrid feedback switching rule based on the common Lyapunov function approach was applied to a Buck converter. The method dealing with switched affine systems was used to study DC-DC converters, and a set of equilibrium points and a class of switching rules were determined in [30, 31]. In order to improve the switching strategy, the clock delay control was discussed in [32]. In addition, the method of state feedback H_∞ controller design for Monrovian switching systems with mixed delays was applied to DC-DC converters in [33]. However, DC-DC converters with uncertain parameters and disturbances have not yet gained sufficient research attention, which motivates the present study.

In this paper, we are interested in investigating the robust H_∞ switching rule design for Boost converters with uncertain parameters and disturbances. Firstly, the Boost converter under consideration is modeled as a switched affine system. Then the common quadratic Lyapunov function approach is utilized for the design of switching rule. By determining a set of attainable equilibrium points, a class of switching rules and the activation region of each subsystem are developed. A sufficient condition for the existence of such switching rule guaranteeing the H_∞ model reference tracking performance is formulated in terms of linear matrix inequality (LMI).

The rest of this paper is organized as follows. Section 2 presents the model of switched affine linear system for a Boost converter with uncertain parameters and disturbances. In Section 3, a switching rule is designed such that the H_∞ model reference tracking performance is satisfied. The simulation result is illustrated through a numerical example in Section 4. Brief conclusion is discussed in Section 5.

Notations. Rⁿ denotes the n-dimensional Euclidean space, and R^n×n is the set of n × n real matrices. For real matrices or vectors, the superscript “T” stands for the transpose. The convex combination is given by , where λ belongs to the set of Λ composed by all nonnegative vectors such that . The space of square integrable functions on [0, ∞) is denoted by L₂[0, ∞).

2. Model of Boost Converter

A Boost converter with the inductor equivalent series resistance (ESR), uncertain parameters, and disturbance is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

A Boost converter with inductor ESR.

Suppose that the converter operates in a continuous current conduction mode. Let the inductor current i and the capacitance voltage u_c be the state variables, and denote that

. From Figure 1, it can be seen that the converter operates between two modes. Considering that the output load resistance R and its variation are bounded, when the switch S is closed, the system equation is

()

when the switch S is open, the system equation is

()

where ω is the disturbance of the input voltage and ΔR₁ and ΔR₂ are the variations of the load resistance.

In order to separate the uncertainties from the system equation, we can use the first-order Taylor series expansion, and the system equation can be written as when the switch S is closed,

()

when the switch S is open,

()

where

()

The uncertainties can be written as

()

where

, and ΔR_max is the upper bound of the variation of the load resistance.

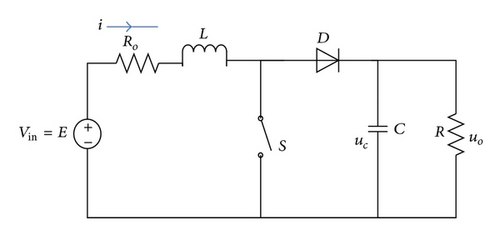
3. Switching Rule Design

Because the hybrid system model of the converter described in Section 2 involves uncertain parameters and disturbance, the model can be described by the following switched affine systems:

()

where x(t) ∈ Rⁿ is the system state, y(t) ∈ R^q is the output, ω ∈ R^p is the bounded exogenous disturbance of the system,

is a piecewise constant function of time, so-called switching rule, and m is the number of system modes. The ith system mode (A_i, b_i, D_i, C_i) is active at time t when σ(t) = i.

, ΔA_i represents the uncertainty, and A_i, b_i, D_i, and C_i are constant matrices of appropriate dimensions.

The problem concerned here is to design a switching rule σ(t) and determine an equilibrium point x_r ∈ Rⁿ that is attainable under such switching rule, that is, x(t) → x_r as t → ∞. Furthermore, the switching rule should guarantee the H_∞ model reference tracking performance.

Given the desired equilibrium point x_r and system (7), the tracking error system is

()

Consider the measurement vector y(t) of system (7), and define the output tracking error as follows:

()

Given a performance index

()

then the problem under consideration can be transformed to design a switching rule σ(t) such that error system (8) is stabilizable with an H_∞ disturbance attenuation γ.

Assumption 1. The uncertainty ΔA_i is given as follow:

()

where M_i and N_i are known constant matrices of the appropriate dimensions and F_i(t) is an unknown bounded function which satisfies

()

Definition 2. Given a constant γ > 0, error switched system (8) is said to be stabilizable with an H_∞ disturbance attenuation γ if there exists a switching rule σ(t) such that the following conditions are satisfied:

(1)
system (8) with ω(t) ≡ 0 is asymptotically stable for all admissible uncertainties;
(2)
under zero-initial condition, that is, x(0) = 0,
()

holds for all admissible uncertainties and all nonzero ω(t) ∈ L₂[0, ∞).

Lemma 3 (see [31].)Consider switched system (7) with b_σ(t) ≡ 0, if there exist λ ∈ Λ and a symmetric positive-definite matrix P ∈ R^n×n such that

()

Then the switching rule

()

makes the equilibrium point x_r = 0 globally asymptotically stable.

Lemma 4 (see [24].)Consider switched affine linear system (7) with m = 2; the point x_r = 0 is a quadratic stabilizable switched equilibrium if and only if there exists α ∈ (0,1) such that

()

Lemma 5 (see [34].)If X and Y are constant matrices of appropriate dimensions, then

()

where ξ is a positive scalar.

The following theorem provides an LMI condition for designing the switching rule σ(t) such that error system (8) is stabilizable with an H_∞ disturbance attenuation γ.

Theorem 6. Let x_r be a given constant vector representing the desired equilibrium point of the system (7), and consider error switched system (8). Given constants γ > 0 and ε > 0, if there exist λ ∈ Λ and a symmetric positive definite matrix P ∈ R^n×n such that

()

for all

, then the following switching rule

()

can make the error switched system (8) stabilizable with an H_∞ disturbance attenuation γ.

Proof. Choose the following Lyapunov function:

()

Along the trajectory of system (8), we obtain from (20) that

()

By Lemma 5, one obtains

()

It follows from (19) and (23) that

()

For any t ≥ 0, the feasibility of (18) implies , which ensures the asymptotic stability of system (8) with ω(t) ≡ 0.

On the other hand, denote that {(t_k, σ(t_k))∣k = 0,1, …, s; 0 = t₀ ≤ t₁ ≤ ⋯≤t_s < t_f} as the switching sequence of σ(t) on the interval [0, t_f). Under zero condition, we have

()

According to Schur’s complement and the inequality (25), it is easy to get

()

Letting t_f = ∞, we get J < 0.

This completes the proof.

From Theorem 6, it can be seen that (18) is a LMI; thus we can first get the matrix P through LMI toolbox of MATLAB [35]. Then the desired switching rule can be obtained from (20) for any selected equilibrium point x_r.

According to the switched affine system model of the Boost converter described in Section 3, if the converter operates in a continuous current conduction mode, we can get m = 2. In the case of two subsystems, if we ignore the uncertainties in the switching point average system, then we can obtain the convex combination as in Lemma 4 and in [8], and the convex combination is given by

()

where

with 0 < λ_i < 1 and

. If the dwell time of the ith subsystem is proportional to λ_i, as the concept of “duty ratio” in DC-DC converters, then (27) is an average model of switched system (7). However, unlike time average control, the quadratic stability of the switched equilibrium takes the state feedback form. A necessary and sufficient condition for the quadratic stability of the switched equilibrium is shown in Lemma 4. In addition, the proposed switching rule depends on state variables; hence rapid switching can be avoided.

Condition (19) is an expression of the desired equilibrium point x_r for DC-DC converters. Notice that the inequality (18) imposes that

is asymptotically stable, where λ_i can be regard as the concept of “duty ratio” in DC-DC converters. Then we can calculate the desired equilibrium point x_r for DC-DC converters by the following equation:

()

where

, 0 < λ_i < 1, and

The switching rule (20) can be expressed as

()

where

()

From (18), we can easily obtain

()

Denote

()

Then the activation regions of subsystems 1 and 2 can be defined as follow:

()

Therefore, the switching rule (20) in the case of two subsystems can be rewritten as

()

where

()

with A_i, M_i, N_i, C_i, and D_i, i = 1,2, have been given in (3), (4), and (6).

Remark 7. In Theorem 6, a method of robust H_∞ switching rule design is proposed for Boost converters. It is worth pointing out that the proposed design method can also be applied to other types of converters that can be described by switched affine system models, such as Buck converters and Buck-Boost converters.

Remark 8. It can be seen from (34) that the matrix P is necessary to the implementation of the switching rule (34); because the matrix P defined in Theorem 6 does not depend on each λ ∈ Λ associated with x_r. Hence, for any equilibrium point selected by the designer, the matrix P can be derived from (18), and consequently, the switching rule (34) can be implemented in practice.

4. Simulation Results

To illustrate the obtained result, consider the Boost converter described in Section 2. The parameters of the Boost converter are E = 12 V, L = 10 mH, C = 100 μF, R = 30 Ω, R₀ = 0.1 Ω, ΔR₁ = sin(θt)Ω, ΔR₂ = cos (θt)Ω, θ = 100, and ω = 0.001e^−100t, and the steady-state duty ratio is 0.5. From (3), (4), and (6), we can obtain

()

Let λ₁ = 0.5, λ₂ = 0.5, ε = 1, and γ = 1000; then we can get

by (28). Solving (18), the matrix P can be obtained as follows:

()

From (34), the desired switching rule can be derived. Figures 2–4 shows the response of the previous Boost converter, where the initial state is given by .

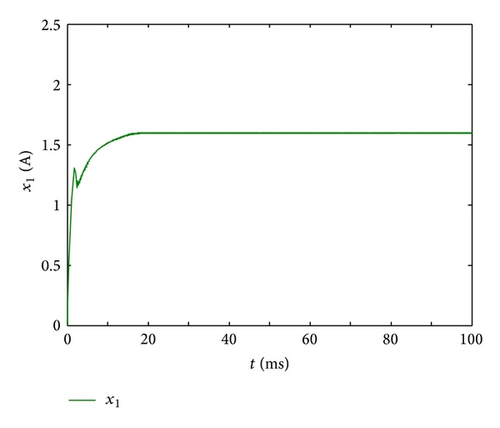
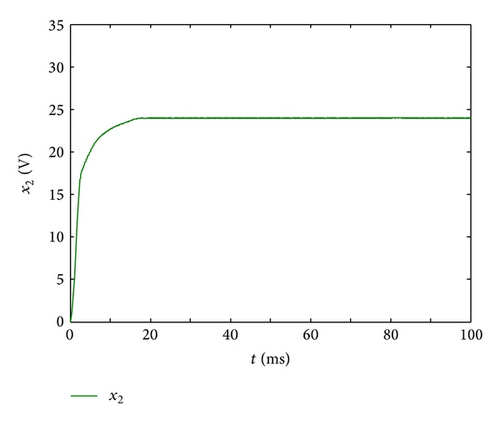
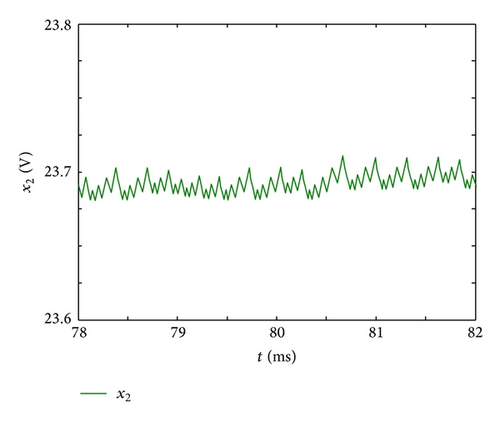
From Figures 2 and 3, it can be observed that the inductor current and capacitance voltage u_c can track the reference current and the reference voltage rapidly, respectively. Therefore, the converter with the switching rule (34) has an H_∞ model reference tracking performance. This demonstrates the effectiveness of the proposed result.

In addition, for this example, when the value of γ is decreased to 393, the feasible solution of (18) cannot be found. Thus, it can be obtained that a larger γ is favorable for the feasibility of matrix inequality (18). On the other hand, we can get from Remark 8 that the solution of (18) does not dependent on the equilibrium point x_r. But the proposed switching rule depends on the equilibrium point x_r, which can be seen from (34).

5. Conclusions

The problem of robust H_∞ switching rule design for Boost converters with uncertain parameters and disturbance has been discussed in this paper. Firstly, a switched linear affine system model for the Boost converter under consideration is built. Then, the state-dependent switching rule is designed for the switched linear affine systems by using common Lyapunov function technique. The simulation result is given to demonstrate that the proposed switching rule can guarantee the H_∞ model reference tracking performance. Our further work will focus on extending the proposed design method to other types of converters. We will also consider the robust H_∞ switching rule design based on min-projection strategy.

Acknowledgment

This work was supported by the National Natural Science Foundation of China under Grant no. 61273120.

References

1 Lin H. and Antsaklis P. J., Stability and stabilizability of switched linear systems: a short survey of recent results, Proceedings of the 20th IEEE International Symposium on Intelligent Control (ISIC ′05), June 2005, 24–29, 2-s2.0-33745217876, https://doi.org/10.1109/.2005.1466986.
10.1109/.2005.1466986
Google Scholar
2 Sun Z., Combined stabilizing strategies for switched linear systems, IEEE Transactions on Automatic Control. (2006) 51, no. 4, 666–674, https://doi.org/10.1109/TAC.2006.872765, MR2228032.
10.1109/TAC.2006.872765
Web of Science® Google Scholar
3 Geromel J. C. and Colaneri P., Stability and stabilization of continuous-time switched linear systems, SIAM Journal on Control and Optimization. (2006) 45, no. 5, 1915–1930, https://doi.org/10.1137/050646366, MR2272172, ZBL1130.34030.
10.1137/050646366
Web of Science® Google Scholar
4 Geromel J. C. and Deaecto G. S., Switched state feedback control for continuous-time uncertain systems, Automatica. (2009) 45, no. 2, 593–597, https://doi.org/10.1016/j.automatica.2008.10.010, MR2527363, ZBL1158.93341.
10.1016/j.automatica.2008.10.010
Web of Science® Google Scholar
5 Shi P. and Boukas E. K., H_∞-control for Markovian jumping linear systems with parametric uncertainty, Journal of Optimization Theory and Applications. (1997) 95, no. 1, 75–99, https://doi.org/10.1023/A:1022683311870, MR1477351, ZBL1026.93504.
10.1023/A:1022683311870
Web of Science® Google Scholar
6 Shi P., Boukas E.-K., and Agarwal R. K., Kalman filtering for continuous-time uncertain systems with Markovian jumping parameters, IEEE Transactions on Automatic Control. (1999) 44, no. 8, 1592–1597, https://doi.org/10.1109/9.780431, MR1707063, ZBL0986.93066.
10.1109/9.780431
Web of Science® Google Scholar
7 Shi P., Boukas E.-K., and Agarwal R. K., Control of Markovian jump discrete-time systems with norm bounded uncertainty and unknown delay, IEEE Transactions on Automatic Control. (1999) 44, no. 11, 2139–2144, https://doi.org/10.1109/9.802932, MR1735731, ZBL1078.93575.
10.1109/9.802932
Web of Science® Google Scholar
8 Shi P., Xia Y., Liu G. P., and Rees D., On designing of sliding-mode control for stochastic jump systems, IEEE Transactions on Automatic Control. (2006) 51, no. 1, 97–103, https://doi.org/10.1109/TAC.2005.861716, MR2192795.
10.1109/TAC.2005.861716
Web of Science® Google Scholar
9 Wu Z. J., Yang J., and Shi P., Adaptive tracking for stochastic nonlinear systems with Markovian switching, IEEE Transactions on Automatic Control. (2010) 55, no. 9, 2135–2141, https://doi.org/10.1109/TAC.2010.2051090, MR2722485.
10.1109/TAC.2010.2051090
Web of Science® Google Scholar
10 Karimi H. R., Robust delay-dependent H_∞ control of uncertain time-delay systems with mixed neutral, discrete, and distributed time-delays and Markovian switching parameters, IEEE Transactions on Circuits and Systems I. (2011) 58, no. 8, 1910–1923, https://doi.org/10.1109/TCSI.2011.2106090, MR2857623.
10.1109/TCSI.2011.2106090
Web of Science® Google Scholar
11 Zhang L., Gao H., and Kaynak O., Network-induced constraints in networked control system—a survey, IEEE Transactions on Industrial Informatics. (2013) 9, no. 1, 403–416.
10.1109/TII.2012.2219540
Web of Science® Google Scholar
12 Wang B., Shi P., Wang J., and Song Y., Novel LMI-based stability and stabilization analysis on impulsive switched system with time delays, Journal of the Franklin Institute. (2012) 349, no. 8, 2650–2663, https://doi.org/10.1016/j.jfranklin.2012.06.005, MR2970347.
10.1016/j.jfranklin.2012.06.005
Web of Science® Google Scholar
13 Li C., Huang T., Feng G., and Chen G., Exponential stability of time-controlled switching systems with time delay, Journal of the Franklin Institute. (2012) 349, no. 1, 216–233, https://doi.org/10.1016/j.jfranklin.2011.10.016, MR2874735, ZBL1254.93136.
10.1016/j.jfranklin.2011.10.016
Web of Science® Google Scholar
14 Zhang L., Shi P., Boukas E.-K., and Wang C., H_∞ model reduction for uncertain switched linear discrete-time systems, Automatica. (2008) 44, no. 11, 2944–2949, https://doi.org/10.1016/j.automatica.2008.03.025, MR2527221, ZBL1152.93321.
10.1016/j.automatica.2008.03.025
Web of Science® Google Scholar
15 Zhang L. and Shi P., l₂-l_∞ model reduction for switched LPV systems with average dwell time, IEEE Transactions on Automatic Control. (2008) 53, no. 10, 2443–2448, https://doi.org/10.1109/TAC.2008.2007860, MR2466605.
10.1109/TAC.2008.2007860
Web of Science® Google Scholar
16 Zhang L. and Shi P., Stability, l₂-gain and asynchronous H_∞ control of discrete-time switched systems with average dwell time, IEEE Transactions on Automatic Control. (2009) 54, no. 9, 2192–2199, https://doi.org/10.1109/TAC.2009.2026841, MR2568668.
10.1109/TAC.2009.2026841
Web of Science® Google Scholar
17 Zhang L. and Shi P., H_∞ filtering for a class of switched linear parameter varying systems, International Journal of Systems Science. (2011) 42, no. 5, 781–788, https://doi.org/10.1080/00207721003764158, MR2775320, ZBL1233.93038.
10.1080/00207721003764158
Web of Science® Google Scholar
18 Ji Z., Wang L., and Xie D., Robust H_∞ control and quadratic stabilization of uncertain switched linear systems, Proceeding of the American Control Conference, July 2004, Boston, Mass, USA, 4543–4548, 2-s2.0-8744280048, https://doi.org/10.1109/ACC.2004.182668.
10.1109/ACC.2004.182668
Google Scholar
19 Xie D., Wang L., Hao F., and Xie G., LMI approach to L₂-gain analysis and control synthesis of uncertain switched systems, IEE Proceedings: Control Theory and Applications. (2004) 151, no. 1, 21–28, 2-s2.0-1542476663, https://doi.org/10.1049/ip-cta:20040010.
10.1049/ip-cta:20040010
Web of Science® Google Scholar
20 Long F., Fei S. M., Fu Z. M. et al., Robust H-infinity state feedback control for switched linear systems with linear fractional uncertainties based on LMI, Proceeding of the Chinese Control Conference, 2005, Guang Zhou, China, 930–934.
Google Scholar
21 Xiang Z., Qiao C., and Mahmoud M. S., Finite-time analysis and H_∞ control for switched stochastic systems, Journal of the Franklin Institute. (2012) 349, no. 3, 915–927, https://doi.org/10.1016/j.jfranklin.2011.10.021, MR2899317.
10.1016/j.jfranklin.2011.10.021
Web of Science® Google Scholar
22 Xiang W. and Xiao J., H_∞ finite-time control for switched nonlinear discrete-time systems with norm-bounded disturbance, Journal of the Franklin Institute. (2011) 348, no. 2, 331–352, https://doi.org/10.1016/j.jfranklin.2010.12.001, MR2771844, ZBL1214.93043.
10.1016/j.jfranklin.2010.12.001
Web of Science® Google Scholar
23 Li Q.-K., Zhao J., Dimirovski G. M., and Liu X.-J., Tracking control for switched linear systems with time-delay: a state-dependent switching method, Asian Journal of Control. (2009) 11, no. 5, 517–526, https://doi.org/10.1002/asjc.132, MR2567083.
10.1002/asjc.132
Web of Science® Google Scholar
24 Bolzern P. and Spinelli W., Quadratic stabilization of a switched affine system about a nonequilibrium point, Proceedings of the American Control Conference, July 2004, 3890–3895, 2-s2.0-8744318489.
Google Scholar
25 Pavlov A., Pogromsky A., Van De Wouw N., and Nijmeijer H., On convergence properties of piecewise affine systems, International Journal of Control. (2007) 80, no. 8, 1233–1247, https://doi.org/10.1080/00207170701261978, MR2354339, ZBL1133.93021.
10.1080/00207170701261978
Web of Science® Google Scholar
26 Xu X., Zhai G., and He S., On practical asymptotic stabilizability of switched affine systems, Nonlinear Analysis. Hybrid Systems. (2008) 2, no. 1, 196–208, https://doi.org/10.1016/j.nahs.2007.07.003, MR2382005, ZBL1157.93502.
10.1016/j.nahs.2007.07.003
Web of Science® Google Scholar
27 Lu Y., Huang X., Zhang B., and Yin L., Hybrid feedback switching control in a buck converter, Proceedings of the IEEE International Conference on Automation and Logistics (ICAL ′08), September 2008, 207–210, 2-s2.0-56449107665, https://doi.org/10.1109/ICAL.2008.4636147.
10.1109/ICAL.2008.4636147
Google Scholar
28 Wu X., Liu C., and Chen W., A unified method for fast modelling of DC-DC switching converters, Journal of the Franklin Institute. (1993) 330, no. 6, 1017–1049, 2-s2.0-43949170095.
10.1016/0016-0032(93)90063-Z
Web of Science® Google Scholar
29 Sreekumar C. and Agarwal V., Hybrid control of a tri-state boost converter, Proceedings of the IEEE International Conference on Industrial Technology (ICIT ′06), December 2006, 121–125, 2-s2.0-51349143972, https://doi.org/10.1109/ICIT.2006.372280.
10.1109/ICIT.2006.372280
Google Scholar
30 Trofino A., Assmann D., Scharlau C. C., and Coutinho D. F., Switching rule design for switched dynamic systems with affine vector fields, Proceedings of the IEEE Conference on Decision and Control and 28th Chinese Control Conference, 2009, 6365–6370.
Google Scholar
31 Deaecto G. S., Geromel J. C., Garcia F. S., and Pomilio J. A., Switched affine systems control design with application to DC-DC converters, IET Control Theory and Applications. (2010) 4, no. 7, 1201–1210, 2-s2.0-77954581360, https://doi.org/10.1049/iet-cta.2009.0246.
10.1049/iet-cta.2009.0246
Web of Science® Google Scholar
32 Xiao W. and Zhang B., Switching rule based on min-projection strategy of DC-DC converters, Proceedings of the Chinese Society of Electrical Engineering. (2009) 29, no. 3, 1–6, 2-s2.0-60149096624.
Google Scholar
33 Karimi H. R. and Shi P., H_∞ control of markovian switching systems with time-delays: applied to DC-DC converters, Proceedings of the 37th Annual Conference of the IEEE Industrial Electronics Society (IECON ′11), November 2011, 3546–3550, 2-s2.0-84856513047, https://doi.org/10.1109/IECON.2011.6119884.
10.1109/IECON.2011.6119884
Google Scholar
34 Petersen I. R., A stabilization algorithm for a class of uncertain linear systems, Systems & Control Letters. (1987) 8, no. 4, 351–357, https://doi.org/10.1016/0167-6911(87)90102-2, MR884885, ZBL0618.93056.
10.1016/0167-6911(87)90102-2
Web of Science® Google Scholar
35 Boyd S., El Ghaoui L., Feron E., and Balakrishnan V., Linear Matrix Inequalities in System and Control Theory, 1994, SIAM, Philadelphia, Pa, USA, https://doi.org/10.1137/1.9781611970777, MR1284712.
10.1137/1.9781611970777
Google Scholar

All articles

Robust H_∞ Switching Rule Design for Boost Converters with Uncertain Parameters and Disturbances

Abstract

1. Introduction

2. Model of Boost Converter

3. Switching Rule Design

4. Simulation Results

5. Conclusions

Acknowledgment

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Robust H∞ Switching Rule Design for Boost Converters with Uncertain Parameters and Disturbances

Abstract

1. Introduction

2. Model of Boost Converter

3. Switching Rule Design

4. Simulation Results

5. Conclusions

Acknowledgment

References

Figures

References

Related

Information

Robust H_∞ Switching Rule Design for Boost Converters with Uncertain Parameters and Disturbances