Volume 2012, Issue 1 958405

Research Article

Open Access

Cluster Synchronization of Time-Varying Delays Coupled Complex Networks with Nonidentical Dynamical Nodes

Shuguo Wang,

Corresponding Author

Shuguo Wang

[email protected]

Department of Mathematics and Physics, Changzhou Campus, Hohai University, Jiangsu, Changzhou 213022, China hhu.edu.cn

Faculty of Science, Jiangsu University, Zhenjiang, Jiangsu 212013, China ujs.edu.cn

Search for more papers by this author

Hongxing Yao,

Hongxing Yao

Faculty of Science, Jiangsu University, Zhenjiang, Jiangsu 212013, China ujs.edu.cn

Search for more papers by this author

Mingping Sun,

Mingping Sun

Faculty of Science, Jiangsu University, Zhenjiang, Jiangsu 212013, China ujs.edu.cn

Search for more papers by this author

Shuguo Wang,

Corresponding Author

Shuguo Wang

[email protected]

Department of Mathematics and Physics, Changzhou Campus, Hohai University, Jiangsu, Changzhou 213022, China hhu.edu.cn

Faculty of Science, Jiangsu University, Zhenjiang, Jiangsu 212013, China ujs.edu.cn

Search for more papers by this author

Hongxing Yao,

Hongxing Yao

Faculty of Science, Jiangsu University, Zhenjiang, Jiangsu 212013, China ujs.edu.cn

Search for more papers by this author

Mingping Sun,

Mingping Sun

Faculty of Science, Jiangsu University, Zhenjiang, Jiangsu 212013, China ujs.edu.cn

Search for more papers by this author

First published: 13 March 2012

https://doi.org/10.1155/2012/958405

Citations: 4

Academic Editor: J. Biazar

Share a link

Email
Wechat
Bluesky

Abstract

This paper investigates a new cluster synchronization scheme in the nonlinear coupled complex dynamical networks with nonidentical nodes. The controllers are designed based on the community structure of the networks; some sufficient criteria are derived to ensure cluster synchronization of the network model. Particularly, the weight configuration matrix is not assumed to be symmetric, irreducible. The numerical simulations are performed to verify the effectiveness of the theoretical results.

1. Introduction

Complex networks model is used to describe various interconnected systems of real world, which have become a focal research topic and have drawn much attention from researchers working in different fields; one of the most important reasons is that most practical systems can be modeled by complex dynamical networks. Recently, the research on synchronization and dynamical behavior analysis of complex network systems has become a new and important direction in this field [1–13]; many control approaches have been developed to synchronize complex networks such as feedback control, adaptive control, pinning control, impulsive control, and intermittent control [14–21].

Cluster synchronization means that nodes in the same group synchronize with each other, but there is no synchronization between nodes in different groups [22–25]; Belykh et al. [26] investigated systems of diffusively coupled identical chaotic oscillators; an effective method to determine the possible states of cluster synchronization and ensure their stability is presented. The method, which may find applications in communication engineering and other fields of science and technology, is illustrated through concrete examples of coupled biological cell models. Wu and Lu [27] investigated cluster synchronization in the adaptive complex dynamical networks with nonidentical nodes by a local control method and a novel adaptive strategy for the coupling strengths of the networks. Ma et al. [28] proposed cluster synchronization scheme via dominant intracouplings and common intercluster couplings. Sorrentino and Ott [29] studied local cluster synchronization for bipartite systems, where no intracluster couplings (driving scheme) exist. Chen and Lu [30] investigated global cluster synchronization in networks of two clusters with inter- and intracluster couplings. Belykh et al. [31, 26] studied this problem in 1D and 2D lattices of coupled identical dynamical systems. Lu et al. [32] studied the cluster synchronization of general networks with nonidentical clusters and derived sufficient conditions for achieving local cluster synchronization of networks. Recently, Wang et al. [33] considered the cluster synchronization of dynamical networks with community structure and nonidentical nodes and with identical local dynamics for all individual nodes in each community by using pinning control schemes. However, there is few theoretical result on the cluster synchronization of nonlinear coupled complex networks with time-varying delays coupling and time-varying delays in nonidentical dynamical nodes.

Motivated by the above discussions, this paper investigates cluster synchronization in the nonlinear coupled complex dynamical networks with nonidentical nodes. The controllers are designed based on the community structure of the networks; some sufficient criteria are derived to ensure cluster synchronization in nonlinear coupled complex dynamical networks with time-varying delays coupling and time-varying delays in dynamic nodes. Particularly the weight configuration matrix is not assumed to be symmetric, irreducible.

The paper is organized as follows: the network model is introduced followed by some definitions, lemmas, and hypotheses in Section 2. The cluster synchronization of the complex coupled networks is discussed in Section 3. Simulations are obtained in Section 4. Finally, in Section 5 the various conclusions are discussed.

2. Model and Preliminaries

The network with nondelayed and time-varying delays coupling and adaptive coupling strengths can be described by

(2.1)

where x_i(t) = (x_i1(t), x_i2(t), …, x_in(t)) ^T ∈ Rⁿ is the state vector of node

describes the local dynamics of nodes in the ϕ_ith community. For any pair of nodes i and j, if ϕ_i ≠ ϕ_j, that is, nodes i and j belong to different communities, then

, is a time-varying delay. H₁(·) and H₂(·) are nonlinear functions. c is coupling strength. A = (a_ij) _N×N, B = (b_ij) _N×N are the weight configuration matrices. If there is a connection from node i to node j (j ≠ i), then the a_ij > 0, b_ij > 0 otherwise, a_ij = a_ji = 0, b_ij = b_ji = 0, and the diagonal elements of matrix A, B are defined as

(2.2)

Particularly, the weight configuration matrix is not assumed to be symmetric, irreducible.

When the control inputs u_i(t) ∈ Rⁿ and v_i(t) ∈ Rⁿ (i = 1,2, …, N) are introduced, the controlled dynamical network with respect to network (2.1) can be written as

(2.3)

where

denotes all the nodes in the ϕ_ith community and

represents the nodes in the ϕ_ith community which have direct links with the nodes in other communities.

The study presents the mathematical definition of the cluster synchronization.

Let {C₁, C₂, …, C_m} denote m (2 ≤ m ≤ N) communities of the networks and If node i belongs to the jth community, then we denote ϕ_i = j. We employ f_i(·) to represent the local dynamics of all nodes in the ith community. Let s_i(t) be the solution of the system where lim _t→∞ ∥s_i(t) − s_j(t)∥ ≠ 0 (i ≠ j); the set S = {s₁(t), s₂(t), …, s_m(t)} is used as the cluster synchronization manifold for network (2.3). Cluster synchronization can be realized if and only if the manifold S is stable.

Definition 2.1 (see [19].)The error variables as for i = 1,2, …, N, where satisfies .

Definition 2.2 (see [19].)Let {1,2, …, N} be the N nodes of the network and {C₁, C₂, …, C_m} be the m communities, respectively. A network with m communities is said to realize cluster synchronization if lim _t→∞e_i(t) = 0 and lim _t→∞∥x_i(t) − x_j(t)∥ ≠ 0 for ϕ_i ≠ ϕ_j.

Lemma 2.3. For any two vectors x and y, a matrix Q > 0 with compatible dimensions, one has 2x^Ty ≤ x^TQx + y^TQ⁻¹y.

Assumption 2.4. For the vector valued function , assuming that there exist positive constants such that f satisfies the semi-Lipschitz condition

(2.4)

for all x, y ∈ Rⁿ and

Assumption 2.5. and is a differential function with and . Clearly, this assumption is certainly ensured if the delay and is constant.

Assumption 2.6 (34) (Global Lipschitz Condition). Suppose that there exist nonnegative constants ϑ, β, for all t ∈ R₊, such that for any time-varying vectors x(t), y(t) ∈ Rⁿ

(2.5)

where ∥ ∥ denotes the 2-norm throughout the paper.

3. Main Results

In this section, a control scheme is developed to synchronize a delayed complex network with nonidentical nodes to any smooth dynamics

. Let synchronization errors

for i = 1,2, …, N, according to system (2.1), the error dynamical system can be derived as

(3.1)

where

for i = 1,2, …, N.

According to the diffusive coupling condition (2.2) of the matrix A, B we have

(3.2)

On the basis of this property, for achieving cluster synchronization, we design controllers as follows:

(3.3)

where

Theorem 3.1. Suppose assumptions 2.4–2.5 hold. Consider the network (2.1) via control law (3.3). If the following conditions hold:

(3.4)

where

. Then, the systems (2.3) is cluster synchronization.

Proof. Construct the following Lyapunov functional:

(3.5)

Calculating the derivative of V(t), we have

(3.6)

By assumptions 2.4–2.6, we obtain

(3.7)

Let

, where ⊗ represents the Kronecker product. Then

(3.8)

By the Lemma 2.3, we have

(3.9)

Therefore, if we have α + ϑcλ_max(Q) + (1/2)β²c²λ_max(PP^T) + (1/(1 − ε))(γ + (1/2)) < d then

(3.10)

Theorem 3.1 is proved completely.

We can conclude that, for any initial values, the solutions x₁(t), x₂(t), …, x_N(t) of the system (2.3) satisfy , that is, we get the global stability of the cluster synchronization manifold S. Therefore, cluster synchronization in the network (2.3) is achieved under the local controllers (3.3). This completes the proof.

Corollary 3.2. When A = 0, network (2.1) is translated into

(3.11)

We design the controllers, as follows, then the complex networks can also achieve synchronization, where

(3.12)

Corollary 3.3. When B = 0, network (2.1) is translated into

(3.13)

We design the controllers, as follows, then the complex networks can also achieve synchronization, where

(3.14)

4. Illustrative Examples

In this section, a numerical example will be given to demonstrate the validity of the synchronization criteria obtained in the previous sections. Considering the following network:

(4.1)

where x_i(t) = (x_i1(t), x_i2(t), x_i3(t)) ^T, f₁(t, x_i(t), x_i(t − τ₁(t))) = D₁x_i(t) + h₁₁(x_i(t)) + h₁₂(x_i(t − τ₁(t))), f₂(t, x_i(t), x_i(t − τ₂(t))) = D₂x_i(t) + h₂₁(x_i(t)) + h₂₂(x_i(t − τ₂(t))) + V, f₃(t, x_i(t), x_i(t − τ₃(t))) = D₃x_i(t) + h₃₁(x_i(t)) + h₃₂(x_i(t − τ₃(t))). k₁ = k₂ = ⋯ = k_N = 10, c = 1, H₁(x) = sin x, H₂(x) = cos x.

In simulation, we choose h₁₁(x_i) = (0, −x_i1x_i3, x_i1x_i2) ^T, h₁₂(x_i) = (0,5x_i2, 0) ^T, h₂₁(x_i) = (0,0, x_i1x_i3) ^T, h₂₂(x_i) = (x_i1, 0,0) ^T, V = [0,0, 0.2] ^T, h₃₁(x_i) = (3.247(|x_i1 + 1| − |x_i1 − 1|), 0,0) ^T, h₃₂(x_i) = (0,0, −3.906 sin (0.5x_i1)) ^T, τ₁(t) = e^t/(1 + e^t), τ₂(t) = 2e^t/(1 + e^t), τ₃(t) = 0.5e^t/(1 + e^t),

(4.2)

Taking the weight configuration coupling matrices

(4.3)

The following quantities are utilized to measure the process of cluster synchronization

(4.4)

where E(t) is the error of cluster synchronization for this controlled network (2.2); E₁₂(t), E₁₃(t), and E₂₃(t) are the errors between two communities; cluster synchronization is achieved if the synchronization error E(t) converges to zero and E₁₂(t), E₁₃(t) and E₂₃(t) do not as t → ∞. Simulation results are given in Figures 1, 2, 3, and 4. From the Figures 1–4, we see the time evolution of the synchronization errors. The numerical results show that Theorem 3.1 is effective.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Time evolution of the synchronization errors E(t).

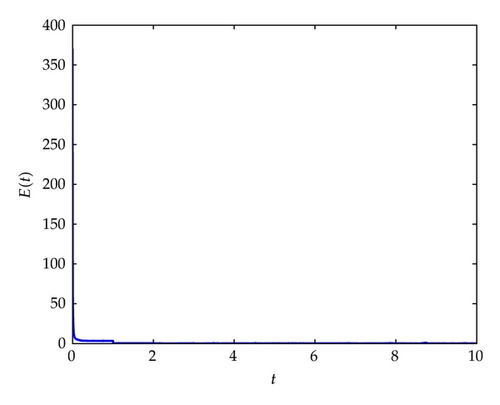
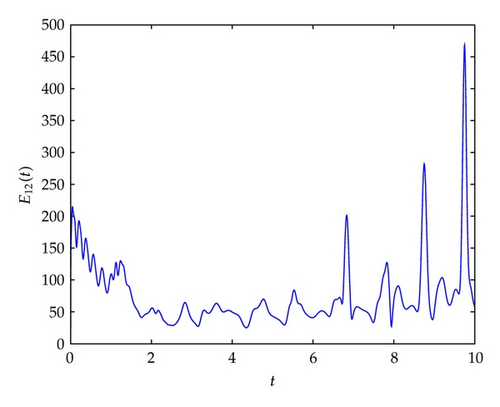
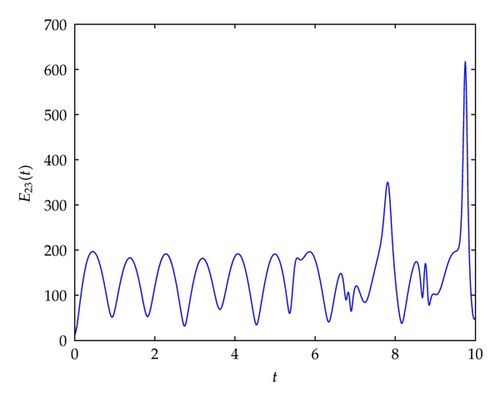
5. Conclusions

The problems of cluster synchronization and adaptive feedback controller for the nonlinear coupled complex networks are investigated. The weight configuration matrix is not assumed to be symmetric, irreducible. It is shown that cluster synchronization can be realized via adaptive feedback controller. The study showed that the use of simple control law helps to derive sufficient criteria which ensure that nodes in the same group synchronize with each other, but there is no synchronization between nodes in different groups is derived. Particularly the synchronization criteria are independent of time delay. The developed techniques are applied three complex community networks which are synchronized to different chaotic trajectories. Finally, the numerical simulations were performed to verify the effectiveness of the theoretical results.

Acknowledgments

This research is partially supported by the National Nature Science Foundation of China (no. 70871056) and by the Six Talents Peak Foundation of Jiangsu Province.

References

1 Cao J., Li P., and Wang W., Global synchronization in arrays of delayed neural networks with constant and delayed coupling, Physics Letters A. (2006) 353, no. 4, 318–325, 2-s2.0-33645876794, https://doi.org/10.1016/j.physleta.2005.12.092.
10.1016/j.physleta.2005.12.092
CAS Web of Science® Google Scholar
2 Chen M., Some simple synchronization criteria for complex dynamical networks, IEEE Transactions on Circuits and Systems II: Express Briefs. (2006) 53, no. 11, 1185–1189, 2-s2.0-34547142768, https://doi.org/10.1109/TCSII.2006.882363.
10.1109/TCSII.2006.882363
Web of Science® Google Scholar
3 Gao H., Lam J., and Chen G., New criteria for synchronization stability of general complex dynamical networks with coupling delays, Physics Letters A. (2006) 360, no. 2, 263–273, 2-s2.0-33750464493, https://doi.org/10.1016/j.physleta.2006.08.033.
10.1016/j.physleta.2006.08.033
CAS Web of Science® Google Scholar
4 He Y., Wang Q.-G., and Zheng W.-X., Global robust stability for delayed neural networks with polytopic type uncertainties, Chaos, Solitons and Fractals. (2005) 26, no. 5, 1349–1354, https://doi.org/10.1016/j.chaos.2005.04.005, 2149320, ZBL1083.34535.
10.1016/j.chaos.2005.04.005
Web of Science® Google Scholar
5 Zhou J., Xiang L., and Liu Z., Global synchronization in general complex delayed dynamical networks and its applications, Physica A. (2007) 385, no. 2, 729–742, https://doi.org/10.1016/j.physa.2007.07.006, 2584888.
10.1016/j.physa.2007.07.006
Web of Science® Google Scholar
6 Han X. P., Lu J.-A., and Chen G. R., Nonlinear integral synchronization of ring networks, Computers & Mathematics with Applications. (2008) 55, no. 4, 808–818, https://doi.org/10.1016/j.camwa.2007.04.037, 2387465, ZBL1161.34025.
10.1016/j.camwa.2007.04.037
Web of Science® Google Scholar
7 Xu S. Y. and Yang Y., Synchronization for a class of complex dynamical networks with time-delay, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 8, 3230–3238, https://doi.org/10.1016/j.cnsns.2008.12.022, 2502399, ZBL1221.34205.
10.1016/j.cnsns.2008.12.022
Web of Science® Google Scholar
8 Jia Z., Wang H., Wang J., and Li Y., The weighted identification of a bipartite-graph complex dynamical network based on adaptive synchronization, Control Theory and Applications. (2010) 27, no. 1, 107–110, 2-s2.0-77950887203.
Google Scholar
9 Wang L., Dai H.-P., Dong H., Shen Y.-H., and Sun Y.-X., Adaptive synchronization of weighted complex dynamical networks with coupling time-varying delays, Physics Letters A. (2008) 372, no. 20, 3632–3639, https://doi.org/10.1016/j.physleta.2008.02.010, 2413862, ZBL1220.90041.
10.1016/j.physleta.2008.02.010
CAS Web of Science® Google Scholar
10 Ji D. H., Park J. H., Yoo W. J., Won S. C., and Lee S. M., Synchronization criterion for Lur′e type complex dynamical networks with time-varying delay, Physics Letters A. (2010) 374, no. 10, 1218–1227, 2-s2.0-74449090303, https://doi.org/10.1016/j.physleta.2010.01.005.
10.1016/j.physleta.2010.01.005
CAS Web of Science® Google Scholar
11 Yuan K., Robust synchronization in arrays of coupled networks with delay and mixed coupling, Neurocomputing. (2009) 72, no. 4–6, 1026–1031, 2-s2.0-58149475227, https://doi.org/10.1016/j.neucom.2008.04.018.
10.1016/j.neucom.2008.04.018
Web of Science® Google Scholar
12 Liu T., Zhao J., and Hill D. J., Synchronization of complex delayed dynamical networks with nonlinearly coupled nodes, Chaos, Solitons and Fractals. (2009) 40, no. 3, 1506–1519, https://doi.org/10.1016/j.chaos.2007.09.075, 2526366, ZBL1197.34092.
10.1016/j.chaos.2007.09.075
Web of Science® Google Scholar
13 Guo W. L., Austin F., and Chen S. H., Global synchronization of nonlinearly coupled complex networks with non-delayed and delayed coupling, Communications in Nonlinear Science and Numerical Simulation. (2010) 15, no. 6, 1631–1639, https://doi.org/10.1016/j.cnsns.2009.06.016, 2576789, ZBL1221.34213.
10.1016/j.cnsns.2009.06.016
Web of Science® Google Scholar
14 DeLellis P., diBernardo M., and Garofalo F., Novel decentralized adaptive strategies for the synchronization of complex networks, Automatica. (2009) 45, no. 5, 1312–1318, https://doi.org/10.1016/j.automatica.2009.01.001, 2531611.
10.1016/j.automatica.2009.01.001
Web of Science® Google Scholar
15 Zheng S., Wang S., Dong G., and Bi Q., Adaptive synchronization of two nonlinearly coupled complex dynamical networks with delayed coupling, Communications in Nonlinear Science and Numerical Simulation. (2012) 17, no. 1, 284–291, https://doi.org/10.1016/j.cnsns.2010.11.029.
10.1016/j.cnsns.2010.11.029
Web of Science® Google Scholar
16 Porfiri M. and di Bernardo M., Criteria for global pinning-controllability of complex networks, Automatica. (2008) 44, no. 12, 3100–3106, https://doi.org/10.1016/j.automatica.2008.05.006, 2531411, ZBL1153.93329.
10.1016/j.automatica.2008.05.006
Web of Science® Google Scholar
17 Sorrentino F., Bernardo M. D., Garofalo F., and Chen G. R., Controllability of complex networks via pinning, Physical Review E. (2007) 75, no. 4, 6, 2-s2.0-34147124485, https://doi.org/10.1103/PhysRevE.75.046103, 046103.
10.1103/PhysRevE.75.046103
CAS PubMed Web of Science® Google Scholar
18 Xia W. and Cao J., Pinning synchronization of delayed dynamical networks via periodically intermittent control, Chaos. (2009) 19, no. 1, 8, https://doi.org/10.1063/1.3071933, 2513764, 013120.
10.1063/1.3071933
PubMed Web of Science® Google Scholar
19 Cai S., Liu Z., Xu F., and Shen J., Periodically intermittent controlling complex dynamical networks with time-varying delays to a desired orbit, Physics Letters A. (2009) 373, no. 42, 3846–3854, https://doi.org/10.1016/j.physleta.2009.07.081, 2552542.
10.1016/j.physleta.2009.07.081
CAS Web of Science® Google Scholar
20 Khadra A., Liu X. Z., and Shen X., Impulsively synchronizing chaotic systems with delay and applications to secure communication, Automatica. (2005) 41, no. 9, 1491–1502, https://doi.org/10.1016/j.automatica.2005.04.012, 2161112, ZBL1086.93051.
10.1016/j.automatica.2005.04.012
Web of Science® Google Scholar
21 Sun W., Hu T., Chen Z., Chen S., and Xiao L., Impulsive synchronization of a general nonlinear coupled complex network, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 11, 4501–4507, https://doi.org/10.1016/j.cnsns.2011.02.032, 2806762, ZBL1222.93102.
10.1016/j.cnsns.2011.02.032
Web of Science® Google Scholar
22 Rabinovich M. I., Torres J. J., Varona P., Huerta R., and Weidman P., Origin of coherent structures in a discrete chaotic medium, Physical Review E. (1999) 60, no. 2, R1130–R1133, 2-s2.0-0001574614, https://doi.org/10.1103/PhysRevE.60.R1130.
10.1103/PhysRevE.60.R1130
CAS Web of Science® Google Scholar
23 Zanette D. H. and Mikhailov A. S., Mutual synchronization in ensembles of globally coupled neural networks, Physical Review E. (1998) 58, no. 1, 872–875, 2-s2.0-0032112573, https://doi.org/10.1103/PhysRevE.58.872.
10.1103/PhysRevE.58.872
CAS Web of Science® Google Scholar
24 Belykh I., Belykh V., Nevidin K., and Hasler M., Persistent clusters in lattices of coupled nonidentical chaotic systems, Chaos. (2003) 13, no. 1, 165–178, https://doi.org/10.1063/1.1514202, 1964970, ZBL1080.37525.
10.1063/1.1514202
CAS PubMed Web of Science® Google Scholar
25 Belykh V. N., Belykh I. V., Hasler M., and Nevidin K. V., Cluster synchronization in three-dimensional lattices of diffusively coupled oscillators, International Journal of Bifurcation and Chaos. (2003) 13, no. 4, 755–779, https://doi.org/10.1142/S0218127403006923, 1980766, ZBL1056.37088.
10.1142/S0218127403006923
Web of Science® Google Scholar
26 Belykh N. V., Belykh I. V., and Mosekilde E., Cluster synchronization modes in an ensemble of coupled chaotic oscillators, Physical Review E. (2001) 63, no. 3, part 2, 2-s2.0-0035276596, 036216.
10.1103/PhysRevE.63.036216
CAS PubMed Web of Science® Google Scholar
27 Wu X. and Lu H., Cluster synchronization in the adaptive complex dynamical networks via a novel approach, Physics Letters A. (2011) 375, no. 14, 1559–1565, 2-s2.0-79952202230, https://doi.org/10.1016/j.physleta.2011.02.052.
10.1016/j.physleta.2011.02.052
CAS Web of Science® Google Scholar
28 Ma Z., Liu Z., and Zhang G., A new method to realize cluster synchronization in connected chaotic networks, Chaos. (2006) 16, no. 2, 9, https://doi.org/10.1063/1.2184948, 2243805, 023103, ZBL1146.37330.
10.1063/1.2184948
PubMed Web of Science® Google Scholar
29 Sorrentino F. and Ott E., Network synchronization of groups, Physical Review E. (2007) 76, no. 5, 10, https://doi.org/10.1103/PhysRevE.76.056114, 2495364, 056114.
10.1103/PhysRevE.76.056114
Web of Science® Google Scholar
30 Chen L. and Lu J., Cluster synchronization in a complex dynamical network with two nonidentical clusters, Journal of Systems Science & Complexity. (2008) 21, no. 1, 20–33, https://doi.org/10.1007/s11424%2D008%2D9063%2D4, 2377222, ZBL1172.93002.
10.1007/s11424-008-9063-4
CAS Web of Science® Google Scholar
31 Belykh V. N., Belykh I. V., and Hasler M., Hierarchy and stability of partially synchronous oscillations of diffusively coupled dynamical systems, Physical Review E. (2000) 62, no. 5, 6332–6345, 2-s2.0-0034317183, https://doi.org/10.1103/PhysRevE.62.6332.
10.1103/PhysRevE.62.6332
CAS Web of Science® Google Scholar
32 Lu W. L., Liu B., and Chen T., Cluster synchronization in networks of distinct groups of maps, European Physical Journal B. (2010) 77, no. 2, 257–264, 2-s2.0-78149285407, https://doi.org/10.1140/epjb/e2010%2D00202%2D7.
10.1140/epjb/e2010-00202-7
CAS Web of Science® Google Scholar
33 Wang K., Fu X., and Li K., Cluster synchronization in community networks with nonidentical nodes, Chaos. An Interdisciplinary Journal of Nonlinear Science. (2009) 19, no. 2, 10, https://doi.org/10.1063/1.3125714, 2548747, 023106.
10.1063/1.3125714
Google Scholar
34 Liu H., Chen J., Lu J. A., and Cao M., Generalized synchronization in complex dynamical networks via adaptive couplings, Physica A. (2010) 389, no. 8, 1759–1770, 2-s2.0-74849084592, https://doi.org/10.1016/j.physa.2009.12.035.
10.1016/j.physa.2009.12.035
CAS Web of Science® Google Scholar

Citing Literature

All articles

Cluster Synchronization of Time-Varying Delays Coupled Complex Networks with Nonidentical Dynamical Nodes

Abstract

1. Introduction

2. Model and Preliminaries

3. Main Results

4. Illustrative Examples

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Cluster Synchronization of Time-Varying Delays Coupled Complex Networks with Nonidentical Dynamical Nodes

Abstract

1. Introduction

2. Model and Preliminaries

3. Main Results

4. Illustrative Examples

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information