A Multiswarm Optimizer for Distributed Decision Making in Virtual Enterprise Risk Management

1. Introduction

Swarm Intelligence (SI) is an innovative artificial intelligence technique for solving complex optimization problems. This discipline is inspired by the collective behaviors of social animals such as fish schools, bird flocks, and ant colonies. In SI systems, there are many simple individuals who can interact locally with one another and with their environments. Although such systems are decentralized, local interactions between individuals lead to the emergence of global behavior and properties.

In recent years, many algorithmic SI methods were designed to deal with practical problems [1–5]. Among them, the most successful is Particle Swarm Optimization (PSO) that drew inspiration from the biological swarming behaviors observed in flocks of birds, schools of fish, and even human social behavior [6–8]. PSO is a population-based optimization tool, which could be implemented and applied easily to solve various function optimization problems. As a problem-solving technique, the main strength of PSO is its fast convergence, which compares favorably with Evolutionary Algorithms (EAs) and other global optimization algorithms [9–12]. However, when solving complex multimodal problems, PSO suffers from the following drawback [13]: as a population evolves, all individuals suffer premature convergence to the local optimum in the first generations. This leads to low population diversity and adaptation stagnation in successive generations. However, such loss of population diversity is not observed in natural systems. Because populations of species interact with one another in natural ecosystems, these species form biological communities which are large social systems typically consist of both heterogeneous and homogeneous aspects. The interaction between species and the complexity of their relationships in these communities exemplify what is meant by the term “symbiosis.” According to different symbiotic interrelationships, symbiotic coevolution can be classified into several categories: mutualism, commensalism, parasitism, and competition. We found that all these types are suitable to be incorporated into the standard PSO model to improve PSO’s performance on complex optimization problems. This should be a general extension of PSO with the purpose of accurately representing as many different forms of symbiotic coevolution as possible.

Thus, inspired by symbiotic cooperation (i.e., mutualism coevolution) phenomenon in nature, this paper proposed a novel multiswarm particle swarm optimizer called PS²O, which extend the single population PSO to interacting multiswarms model by constructing hierarchical interaction topologies and enhanced dynamical update equations. In PS²O, we implement a hierarchical interaction topology that consists of two levels (i.e., individual level and swarm level), in which information exchanges take place permanently. Each individual of the proposed model evolves based on the knowledge integration of itself (associate with individual’s own cognition), its swarm members (associate social interaction within each swarm), and its symbiotic partners from other swarm (associate heterogeneous cooperation between different swarms). That is, we extend the control law (i.e., the dynamic update equation) of the canonical PSO model by adding a significant ingredient, which takes into account the symbiotic coevolution (or heterogeneous cooperation) between different swarms. By incorporating this new degree of complexity, PS²O can accommodate a considerable potential for solving more complex problems. Here we provide some initial insights into this potential by evaluating PS²O on both mathematical benchmark functions and a complex real-world problem-risk management in a virtual enterprise (VE). The 5 benchmark functions used in our experiments have been widely employed by other researchers to evaluate their algorithms [14–16]. In this paper, the risk management problem in VE is modeled as a distributed decision-making (DDM) system. This novel risk management model is a complex hierarchical optimization problem with two levels, namely, the top model and the base model, which take care of the continuous decision variables and the discrete ones, respectively. The simulation results, which are compared to other methods, are reported in this paper to show the merits of the proposed algorithm.

The paper is organized as follows. Section 2 gives a review of the canonical PSO algorithm and several multi-swarm PSO variants. Section 3 describes the proposed multi-swarm coevolution algorithm. In Section 4, it will be shown that PS²O outperforms the canonical PSO and its variants on 5 benchmark test functions. Section 5 describes the risk management optimization model in VE and a detailed design algorithm of risk management by PS²O. The simulation result of risk management in a VE based on PS²O compared with canonical PSO is also presented in this section. Finally, conclusions are drawn in Section 6.

2. Review of Canonical Particle Swarm Optimization

3. PS²O Algorithm

Straight PSO uses the analogy of a single-species population and the suitable definition of the particle dynamics and the particle information network (interaction topology) to reflect the social evolution in the population. However, the situation in nature is much more complex than what this simple metaphor seems to suggest. Indeed, in biological populations there is a continuous interplay between individuals of the same species, and also encounters and interactions of various kinds with other species [19]. The points at issue can be clearly seen when one observes such ecological systems as symbiosis, host-parasite systems, and prey-predator systems, in which two organisms mutually support each other, one exploits the other, or they fight against each other. For instance, mutualistic relations between plants and fungi are very common. The fungus invades and lives among the cortex cells of the secondary roots and, in turn, helps the host plant absorb minerals from the soil. Another well-known example is the “association” between the Nile crocodile and the Egyptian plover, a bird that feeds on any leeches attached to the crocodile’s gums, thus keeping them clean. This kind of “cleaning symbiosis” is also common in fish.

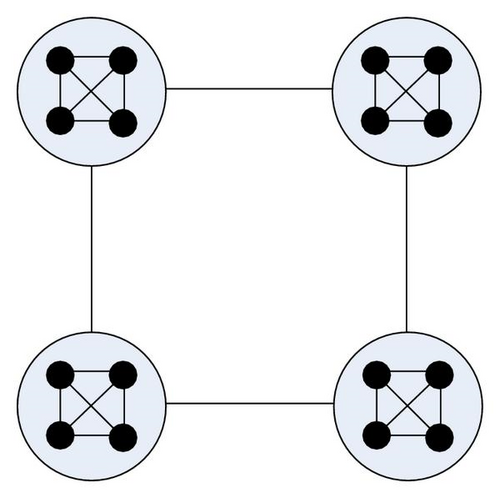
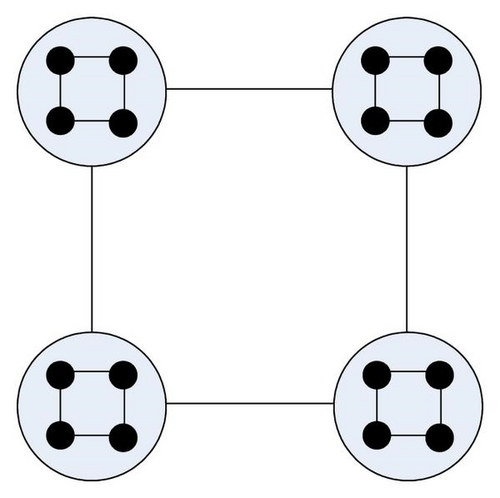
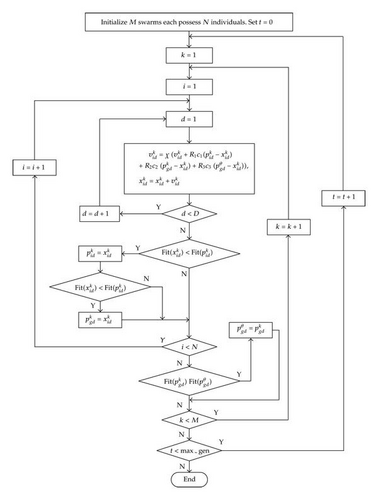
We should note that, for solving discrete problems, we still use (2.4) and (2.5) to discrete the position vectors in PS²O algorithm. The pseudocode for the PS²O algorithm is listed in Table 1. The flowchart of the PS²O algorithm is presented in Figure 2, and according variables used in PS²O are summarized in Table 2.

4. Benchmark Test

4.1. Test Function

A set of 5 benchmark functions, which are commonly used in evolutionary computation literature [16, 20] to show solution quality and convergence rate, was employed to evaluate the PS²O algorithm in comparison to others. The first problem is the unimodal Sphere function that is easy to solve. The second problem is the Rosenbrock function, which has a narrow valley from the perceived local optima to the global optimum and can be treat as a multimodal problem. The remaining three functions are multimodal problem. Griewank’s function has a $$ component causing linkages among variables, thereby making it difficult to reach the global optimum. The Weierstrass function is continuous but differentiable only on a set of points. The composition functions are a set of novel challenging problems, which are constructed using some basic benchmark function with a random located global optimum and several randomly located deep local optima. The Gaussian function is used to combine the basic functions and blur the function structures. CF1 is constructed using 10 sphere functions which is an asymmetrical multimodal function with 1 global optimum and 9 local optima (the landscape of CF1 is illustrated in Figure 3). The variables of the CF1 formulation can be referred to [20]. The formulas of these functions are presented below.

• (1)

  Sphere function:

  $$ (4.1)

• (2)

  Rosenbrock function:

  $$ (4.2)

• (3)

  Griewank function:

  $$ (4.3)

• (4)

  Weierstrass function:

  $$ (4.4)
  where a = 0.5, b = 3, kmax  = 20.

• (5)

  Composition function 1:

  $$ (4.5)

where  n is the number of basic function, w_i is weight value for each f_i(x),   f_i(x) is ith basic function used to construct the composition function (here f₁–f₁₀: Sphere Function), o_i is new shifted optimum position for each f_i(x),   o_iold is old optimum position for each f_i(x), λ_i  is used to stretch or compress the function, M_i is orthogonal rotation matrix for each f_i(x), and bias_i is defines which optimum is global optimum.

4.2. Experimental Setting

Experiments were conducted with PS²O compared with four successful variants of PSO:

• (i)

  local version of PSO with constriction factor (CPSO) [21];

• (ii)

  fully informed particle swarm (FIPS) [22];

• (iii)

  unified particle swarm (UPSO) [23];

• (iv)

  fitness-distance-ratio-based PSO (FDR-PSO) [24].

Among these variations, UPSO combined the global version and local version PSO together to construct a unified particle swarm optimizer; FIPS used all the neighbors’ knowledge of the particle to update the velocity; the FDR-PSO selects one other particle, which has a higher fitness value and is nearer to the particle being updated, to update each velocity dimension.

The number of swarms M needs be tuned. Three 10D functions, namely Sphere, Rosenbrock, and Griewank, are used to investigate the impact of this parameter. Experiments were executed by changing the number of swarms and fixing each swarm size at 10. The average test results obtained form 30 runs are plotted in Figure 4. From Figure 4, we can observe that the performance of PS²O is influenced by M. When M increases, we obtained faster convergence velocity and better results.

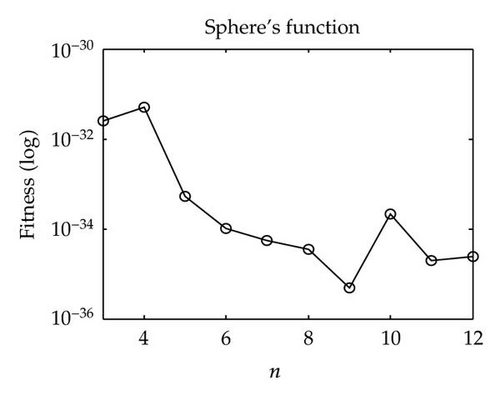
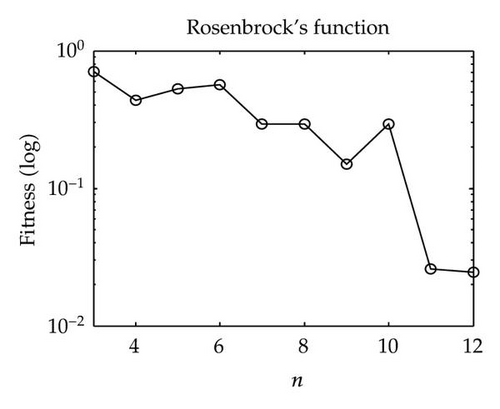
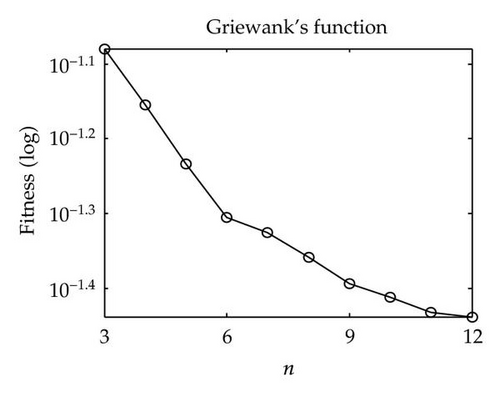
For fair comparison, the population size of all algorithms used in our experiments was set at 100 (all the swarms of PS²O include the same particle numbers of 10). The maximum velocity of all PSO variants was set to be 5% of the search space for unimodal functions and 50% for multimodal functions. For canonical PSO and UPSO, the learning rates c₁ and c₂ were both 2.05 and the constriction factor χ = 0.729. For FIPS, the constriction factor χ equals 0.729 and the U-ring topology that achieved highest success rate is used. For FDR-PSO, the inertia weight ω started at 0.9 and ended at 0.5 and a setting of c₁ = c₂ = 2.0 was adopted. For PS²O, the interaction topology illustrated in Figure 1(b) is used; the constriction factor in PS²O is also used with χ = 0.729 according to Clerc’s method; correspondingly, the ϕ coefficient must sum to 4.1 and then the learning rates c₁ = c₂ = c₃ = ϕ/3 ≈ 1.3667.

4.3. Simulation Results

The experiment runs 50 times, respectively, for each algorithm on each benchmark function of 30 dimensions. The numbers of generations were set to be 10000. The representative results obtained are presented in Table 4, including the best, worst, mean, and standard deviation of the function values found in 50 runs. Figures 5, 6, 7, 8, and 9 presents the evolution process for all algorithms according to the reported results in Table 3.

Table 3. Performance of all algorithms. In bold are the best results.

Func. (dim.30)		PS2O	CPSO	FIPS	UPSO	FDR-PSO
f1	Best	0	2.4787e − 116	1.1874e − 030	3.4459e − 185	6.9665e − 190
	Worst	0	1.3486e − 113	9.7762e − 029	1.9929e − 182	7.4365e − 168
	Mean	0	2.4205e − 114	1.7391e − 029	3.7072e − 183	2.4789e − 169
	Std	0	3.3966e − 114	2.2995e − 029	0	0
f2	Best	1.5203e − 015	5.8889	17.4217	0.7070	0.0012
	Worst	5.1336e − 014	7.4375	23.4450	4.0368	4.0879
	Mean	1.0412e − 014	6.6172	22.5407	2.0983	0.2797
	Std	9.7087e − 015	0.4028	1.2748	0.7696	1.0224
f3	Best	0	0	0	0	0
	Worst	0	0.1152	0.0123	0.0388	0.0737
	Mean	0	0.0183	0.0016	0.0347	0.0179
	Std	0	0.0266	0.0038	0.0478	0.0182
f4	Best	0	2.8242e − 005	0	0	0
	Worst	0	3.7591	0.2856	8.1054	1.5086
	Mean	0	1.3510	0.0201	4.4244	0.1581
	Std	0	1.1606	0.0558	2.6022	0.4569
f5	Best	0	0.0051	0	0	0
	Worst	0	100.0071	45.5672	0.0467	300.00
	Mean	0	50.0061	33.7051	0.0136	100.00
	Std	0	70.7121	25.8645	0.0143	141.42

Table 4. Criterion of risk rating.

Value of risk probability	Risk level
[0.00, 0.38]	Low risk
(0.38, 0.67]	Medium risk
(0.67, 1.00]	High risk

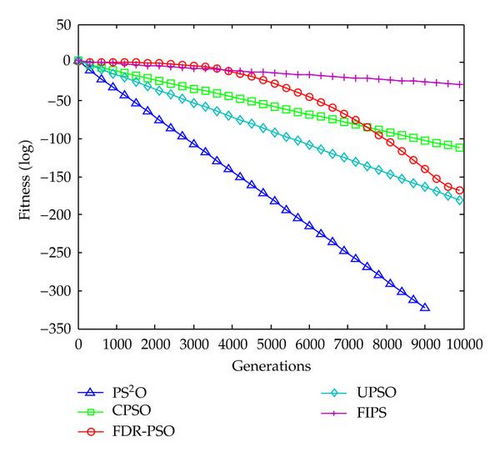
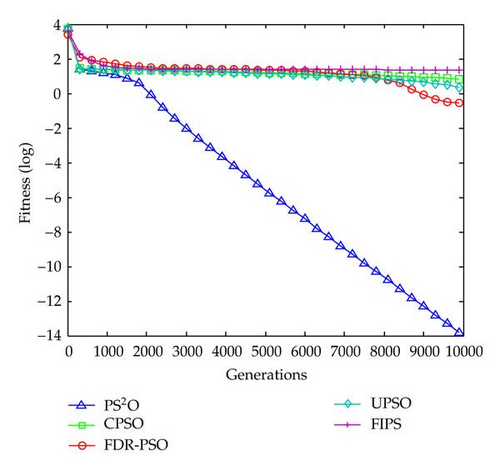
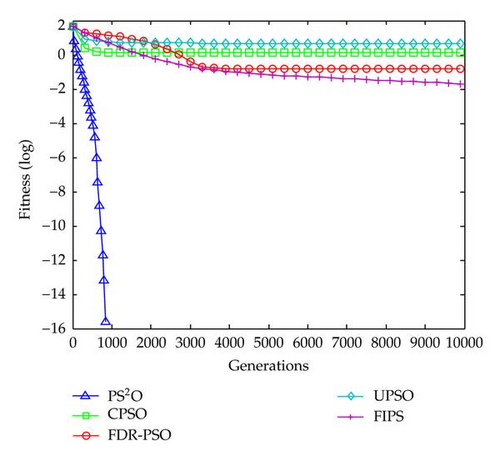
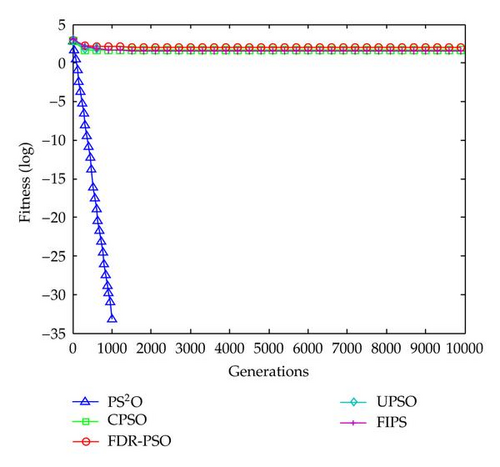
From the results, we can observe that the PS²O algorithm obtains an obviously remarkable performance. We can see it clearly that PS²O converged with greatly faster speed to significantly better results than the other PSO variants for both unimodal and multimodal cases. It should be mentioned that the PS²O were the only ones able to consistently find the minimum of the Sphere function, Griewank’s function, Weierstrass function, and Composition function 1, while the other algorithms generated poorer results on them. The result on Rosenbrock obtained by PS²O is also very good. Since a result within 40.0 on 30 D Rosenbrock reported in other EA and SI works is considered well, the PS²O algorithm’s performance on Rosenbrock function is remarkable good.

With the hierarchical interaction topology, a suitable diversity in the whole population can be maintained. At the same time, the enhanced dynamical update rule significantly speeds up the multi-swarm to converge to the global optimum. Because of this, the PS²O performs considerably better than many PSO variants.

5. Virtual Enterprise Risk Management Based on PS²O

A virtual enterprise (VE) [25] is a temporary consortium of autonomous, diverse, and possibly geographically dispersed organizations that pool their resource to meet short-term objectives and exploit fast changing market trends. A VE is a dynamic alliance of member companies (owner and partners), which join to take advantage of a market opportunity. Each member company will provide its own core competencies in areas such as marketing, engineering, and manufacturing to the VE. When the market opportunity has passed, the VE is dissolved. In a VE environment, there are various sources of risks that may threaten the security of VE, such as market risk, credit risk, operational risk, and others [26]. Recently, risk management of a VE has attracted much research attention.

5.1. The Two-Level Optimization Model for Risk Management in a Virtual Enterprise

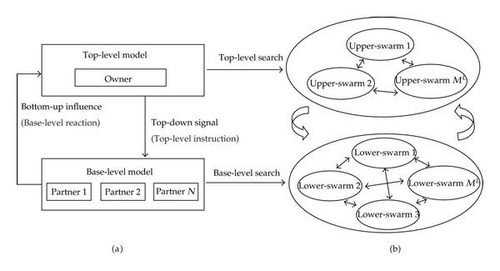
In this paper, the two-level risk manage model suggested by Huang and Lu [27] is employed to evaluate the performance of the proposed PS²O algorithm. This model can be described as a two-level Distributed Decision Making (DDM) system that is depicted in Figure 10(a).

In the top level, the decision maker is the owner who allocates the budget (i.e., the risk cost investment) to each member of VE. The decision variables are therefore given by I = (I₀, I₁, …, I_n). Here I₀ denotes the budget to owner and I_i (i = 1,2, …,   n) represents the budget to Partner i. That is, there are n + 1 members in a VE. Then the top-level objective of risk management in a VE is to best allocate the budget of each member so as to minimize the total risk level of the VE. The top-level model can be formulated as a continuous optimization problem that is given in what follows:

$$ (5.1)

where R_i(I_i)  is the risk level of ith member under risk cost investment I_i, w_i represents the weight of member i, I_max is the maximum total investment budget, and R_max stands for the maximum risk level for each member in the VE.

In the base level, the partners of VE are making their decisions in view of the top-level’s instruction (i.e., the budget to partners). The base-level risk management is that the decision makers select the optimal series of risk control actions $$ for each partner i  (i = 1,2, …, n) to minimize the risk level with respect to the allocated budget I_i. Here m is the number of risk factors that affect each partner’s security. Then the base-level model can be formulated as a discrete optimization problem that is given in what follows:

$$ (5.2)

where R_i(A_i | I_i) is the risk level of ith partner under risk control action A_i with respect to the top-level investment budget I_i, $$ represents the cost of partner i under the risk control action $$ for the risk factor j, and W stands for the number of available actions for each risk factor of each partner.

5.2. Risk Management in VE Based on PS²O

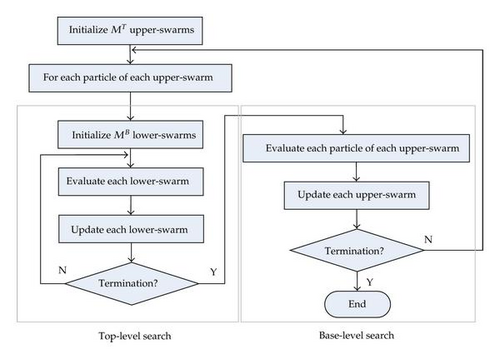
The detailed design of risk management algorithm based on PS²O is introduced in this section. Since the optimizing problem has a two-level hierarchical structure, this risk management algorithm is composed of two types of swarms that search in different levels, respectively, namely, the upper swarm and the lower swarm. The algorithm design reflects a two-phase searching process as Figure 10(b) illustrates. In the top-level searching process, the upper swarms that are designed based on the continuous PS²O, search a continuous space for the investment budget allocation for all VE members. While the lower swarms, which are designed based on the discrete PS²O, receive information from upper swarms, and must search the discrete space for a best action combination for risk management of all partners. The overall searching process can be described as follows.

(1) Particle Representation

(a) Definition of Continuous Particle In each upper-swarm, each particle has a dimension equal to n + 1  (i.e., the number of VE members). Each particle has a real number representation and is a possible allocation of investment budget for all members. The ith particle of the kth upper swarm is defined as follows:

$$ (5.3)

For example, a real-number particle (286.55, 678.33, 456.78, 701.21, 567.62) is a possible allocation of investment budget of 5 VE members. The first bit means that the owner received investment of 286.55 units. The 2 to 5 bits mean that the amount of investment allocated to partner 1 to 4 is 678.33, 456.78, 701.21, and 567.62 respectively.

(b) Definition of Discrete Particle For the lower swarms, in order to appropriately represent the action combination by a particle, we design an “action-to-risk-to-partner” representation for the discrete particle. Each discrete particle in each lower swarm has a dimension equal to the number of n × m × W, here W is the number of available actions for each risk factor, m is the number of risk factors of each partner, and n is the number of VE partners. The ith particle of the kth lower swarm is defined as follows:

$$ (5.4)

where $$ equals 1 if the risk factor β of VE partner α is solved by the γth action and 0 otherwise. For example, set n = 2,   m = 4,   W = 4, suppose the action combination of two partners is (2314, 2401), here 0 stands for no action is selected for the third risk factor of the second partner in VE. By our definition, we have $$ and all other $$ (see Figure 11).

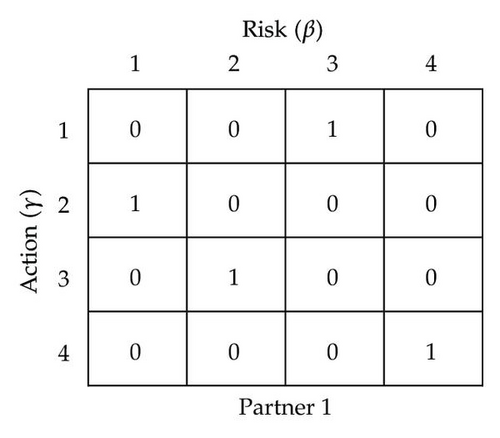
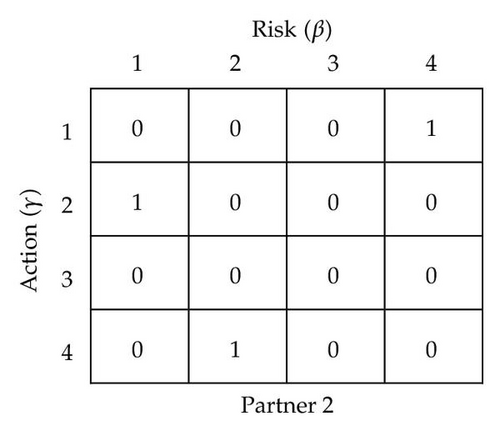
(2) Risk Management Procedure The processing performed by this algorithm is best illustrated in the diagram given in Figure 12.

Step 1. The first step in top level is to randomly initialize M^T upper swarms each possesses N^T particles (totally M^T × N^T individuals). Each particle $$ in the top level is an instruction and is communicated to the base level to drive a base level search process (Steps 2–4).

Step 2. For each top-level instruction $$, the base-level randomly initialize M^B lower swarms each possesses N^B particles (totally M^B × N^B individuals). At each iteration in base level, for each particle $$ (i.e., the ith particle of the kth lower-swarm), evaluate its fitness using the base-level optimization function as follows:

$$ (5.5)

where u_β is the weight of the risk factor β, d_λ  is the value corresponding to the risk rating λ, l is the number of risk ratings, and φ is the punishment coefficient. $$ and $$ is defined as the position index of 1 in $$. For example, if $$, the value of $$ is 3. $$ is a convex decreasing function, which is approximated by

$$ (5.6)

to assesses the probability of risk occurrence at risk rating λ under action $$. Here the parameter θ_βλ is used to describe the effects of different risk factors under different risk ratings. The cost of the action $$ is assumed to be a concave increasing function of the corresponding action, which is approximated by

$$ (5.7)

and the parameter $$ describes the effects of different risk factors of different partners. The notation (·) ⁺ is defined as follows:

$$ (5.8)

Step 3. Compare the evaluated fitness values and select pbest, sbest, and cbest for each lower swarm. Then update the velocity $$ of each base level particle according to (3.1). For our problem, each partner can only select one action for each risk factor or do nothing with this factor. In order to take care of this problem, for each particle, action γ is selected for risk factor β of partner α according to following probability:

$$ (5.9)

Then the position of each base-level particle is updated by Algorithm 1.

Step 4. The base-level search process is repeated until the maximum number of base-level iteration is met. Then send the last best base-level decision variable $$ to the top-level for the fitness computation of the top-level particle $$.

Step 5. With the base-level reaction $$, each top-level particle $$ is evaluated by the following top-level fitness function:

$$ (5.10)

where ϕ and η is the punishment coefficient and the risk level of the owner $$ is approximated by a convex decreasing function as follows:

$$ (5.11)

Step 6. Compare the evaluated fitness values and select pbest, sbest, and cbest for each upper swarm. Then update the velocity and position of each top-level particle according to (3.1) and (3.2). The top-level computation is repeated until the maximum number of top-level iteration is met.

Algorithm 1

• Begin

• Let X^temp be a zero vector that has a dimension equal to n × m × W.

• For  (α = 1  to  n)

•  For  (β = 1  to  m)

•   For  (γ = 1  to  W)

•    If  (rand   ≤ p_i(αβγ)k)

•     //Action  γ is selected for risk  β of partner  α

• $$;

•     Break;

•    End if

•   End for

•  End for

• End for

• $$

• END

5.3. An Illustrative Example

In this section, a numerical example of a VE is conducted to validate the capability of VE risk management based on the proposed PS²O. In order to show the superiority of PS²O, the risk management algorithm designed by canonical PSO is also applied to the same case.

In this case, the VE is constructed by one owner and four partners (i.e., n = 4) and the total investment is B_max = 3500; 10 risk factors are considered for each partner and 4 actions can be selected for each risk factor (i.e., m = 10 and W = 4); the number of risk ratings l = 3 and the value of each rating is d₁ = 0.165, d₂ = 0.335, and d₃ = 0.500, respectively (according to the values of ratings, the criterion of risk rating is shown in Table 4); the maximum risk level R_max = 0.67, which means that the risk level of each member must be below the medium level; the weight of risk level of each VE member is w₀ = w₁ = w₂ = w₃ = w₄ and the weights u_β of each risk factors for each partner are listed in Table 5; the values of the parameter θ_βλ and $$ are presented in Tables 6 and 7, respectively; the punishment coefficient ϕ, η, and φ are given as 1.5, 28 and 0.2.

Table 5. The weights of the risk factors.

Risk factor	1	2	3	4	5	6	7	8	9	10
uβ	0.1	0.15	0.10	0.05	0.10	0.10	0.15	0.10	0.05	0.10

Table 6. The summary of parameter θ_βλ.

β	λ
	1	2	3
1	0.10	0.07	0.13
2	0.23	0.20	0.17
3	0.33	0.27	0.30
4	0.37	0.40	0.43
5	0.50	0.47	0.53
6	0.63	0.57	0.60
7	0.73	0.70	0.67
8	0.83	0.77	0.80
9	0.87	0.90	0.93
10	1.00	0.97	1.03

Table 7. The summary of parameter $$.

Risk factor	1	2	3	4	5	6	7	8	9	10
$$	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0

In applying PS²O and PSO to this case, the continuous and binary algorithms are used in top level and base level of the optimization model respectively. For the top-level algorithms, the maximum generation in each execution for each algorithm is 100; the initialized population size of 10 particles is the same for PS²O and PSO, while the whole population is divided into 2 swarms (each possesses 5 individuals) for PS²O in the initialization step; the interaction topology illustrated in Figure 1(a) is used for continuous PS²O; the other parameters of continuous PS²O and PSO were set to the same values as in Section 4. For the base-level algorithms, the maximum generation for each algorithm is 100; the initialized population size of 20 particles is the same for PS²O and PSO, while the whole population is divided into 4 swarms (each possesses 5 individuals) for PS²O in the initialization step; the interaction topology illustrated in Figure 1(b) is used for binary PS²O; the other parameters of binary PS²O and PSO were set to the same values as in Section 4. The experiment runs 30 times, respectively, for each algorithm.

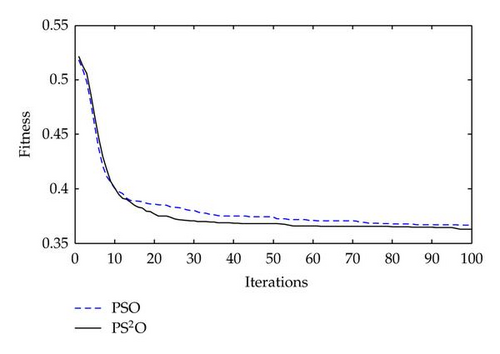
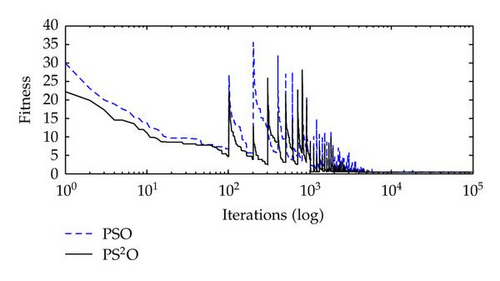
The top-level and base-level search progresses of the averaged best-so-far fitness values over 20 runs are shown in Figures 13 and 14, respectively. It should be noted that the total iteration of base-level searching is 100 (base-level maximum generation) ×10 (top-level population size) ×10 (top-level maximum generation) = 10⁴. That is, the base-level algorithms will be restarted after every 100 iterations. From the figures, we can see that PS²O converges with a higher speed compared to PSO and obtains better results in both levels searching progresses.

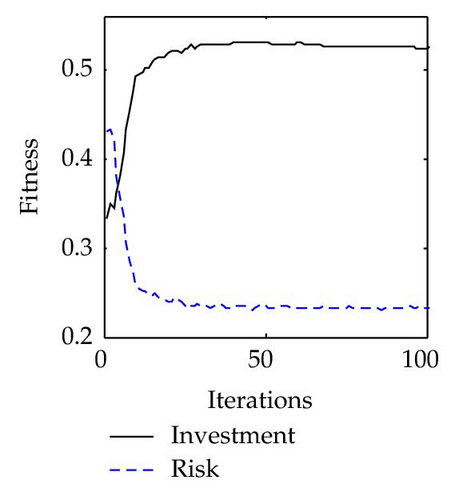
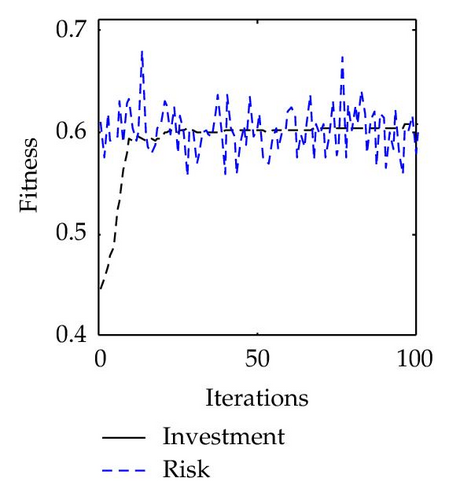
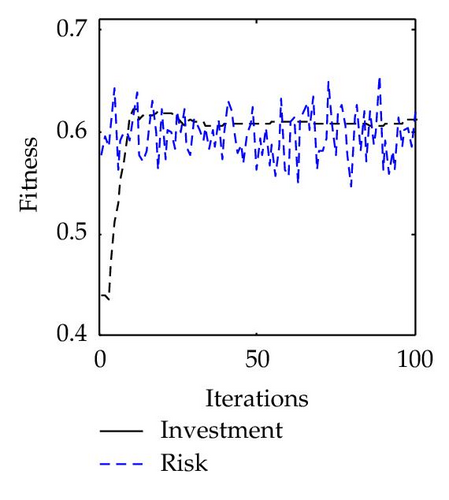
The average solutions over 30 runs obtained by PS²O and PSO are summarized in Table 8. Before proceeding with the risk management procedure, the risk levels are one for both the VE and the partner, which is a high risk level. Table 8 shows that the resulting risk levels of the VE and the owner are in the low risk level, while all the partners are in the medium risk level. Therefore the budget and the actions selected by the owner and the partner are very effective to reduce the risk of the VE.

Table 8. Simulation results of both algorithms.

Value of risk probability	PSO	PS2O
Risk level of VE	0.3667	0.3628
Risk level of owner	0.2268	0.2340
Risk level of partner	0.6191, 0.6172, 0.6006, 0.6285	0.6148, 0.6180, 0.5694, 0.5751
Total budget	3.4455e + 003	3.4223e + 003
Each member’s budget	754.12, 670.47, 693.35, 674.78, 652.81	734.17, 668.18, 673.69, 684.84, 661.39

To fully demonstrate the risk management performance using the PS²O algorithm, risk investment budget, and risk level controlling processes of each VE member based on PS²O is shown in Figure 15. Generally, an effective actions sequence corresponds to a higher cost and a lower risk level. From the figures, it can be concluded that the additional cost of selecting effect actions can not result in a remarkable decrease in the risk level.

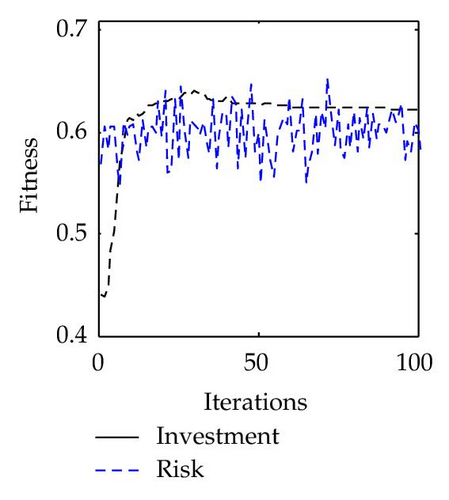
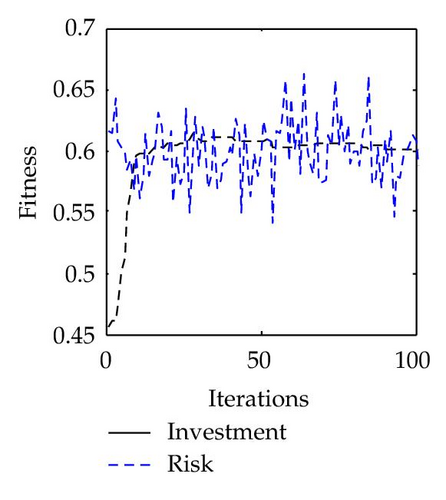
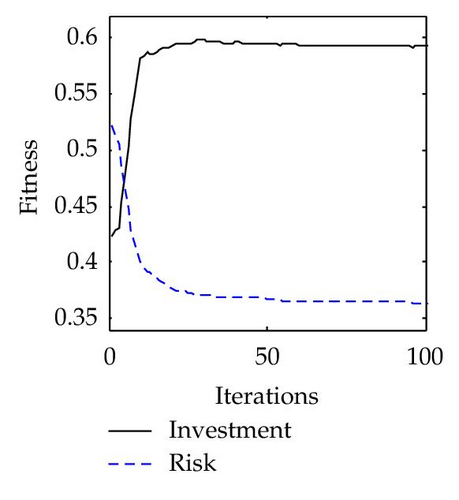
6. Conclusions

In this paper, we develop an optimization model for minimizing the risks of the virtual enterprise based on a novel multi swarm optimizer PS²O. In PS²O, the hierarchical interaction topology consists of two levels (i.e., the individual level and the swarm level), in which information exchanges take place not only between the particles within each swarm but also between different swarms. The dynamical update equations of our multi-swarm approach are enhanced by a significant ingredient, which takes into account the symbiotic coevolution (or heterogeneous cooperation) between different swarms. Because of this, each individual of the proposed model evolves based on the knowledge integration of itself (associate with individual’s own cognition), its swarm members (associate social interaction within each swarm), and its symbiotic partners from other swarm (associate heterogeneous cooperation between different swarms). With five mathematical benchmark functions, PS²O is proved to have significantly better performance than four successful variants of PSO.

In the proposed risk management model of VE, a two-level optimization scheme was introduced to describe the decision processes of the owner and the partners. This DDM model considers the situation that the owner allocates the budget to each member of the VE in order to minimize the risk level of the VE. Accordingly, a transfer optimization model, which can easily use EA and SI algorithms to treat the risk manage problem in VE, is elaborately developed. PS²O is then employed to solve the real-world VE risk management problem. The simulation studies, which compared to Canonical PSO algorithm, show that the PS²O obtains superior risk management solutions than PSO methods in terms of optimization accuracy and convergence speed.