Journal of Applied Mathematics
Volume 2012, Issue 1 872161
Research Article
Open Access

Nonlinear Periodic Oscillation of a Cylindrical Microvoid Centered at an Isotropic Incompressible Ogden Cylinder

Wenzheng Zhang, 

Wenzheng Zhang

State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics, Faculty of Vehicle Engineering and Mechanics, Dalian University of Technology, Dalian 116024, China dlut.edu.cn

Search for more papers by this author
Xuegang Yuan, 

Corresponding Author

Xuegang Yuan

State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics, Faculty of Vehicle Engineering and Mechanics, Dalian University of Technology, Dalian 116024, China dlut.edu.cn

School of Science, Dalian Nationalities University, Dalian 116600, China dlnu.edu.cn

Search for more papers by this author
Hongwu Zhang, 

Hongwu Zhang

State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics, Faculty of Vehicle Engineering and Mechanics, Dalian University of Technology, Dalian 116024, China dlut.edu.cn

Search for more papers by this author
First published: 24 December 2012
https://doi.org/10.1155/2012/872161
Academic Editor: Kale Oyedeji

Abstract

We study the dynamic mathematical model for an infinitely long cylinder composed of an isotropic incompressible Ogden material with a microvoid at its center, where the outer surface of the cylinder is subjected to a uniform radial tensile load. Using the incompressibility condition and the boundary conditions, we obtain a second-order nonlinear ordinary differential equation that describes the motion of the microvoid with time. Qualitatively, we find that this equation has two types of solutions. One is a classical nonlinear periodic solution which describes that the motion of the microvoid is a nonlinear periodic oscillation; the other is a blow-up solution. Significantly, for the isotropic incompressible Ogden material, there exist some special values of material parameters, the phase diagrams of the motion equation have homoclinic orbits, which means that the amplitude of a nonlinear periodic oscillation increases discontinuously with the increasing load.

1. Introduction

Cylindrical structures are very common used in social productions and human lives. The researches on the dynamic oscillation problems of such structures composed of hyperelastic materials are of important significance. As is well known, such problems can be formulated as initial (boundary) value problems of nonlinear evolution equation(s). Knowles [1] firstly studied the free radial oscillation of an incompressible cylindrical tube composed of an isotropic Mooney-Rivlin material; in the limiting case of a thin walled cylindrical tube, the equation reduces to the Ermakov-Pinney equation. Then, Shahinpoor and Nowinski [2] and Rogers and Baker [3] used the nonlinear superposition principle for the Ermakov-Pinney equation to derive solutions. The works appeared in this area have been reviewed by Rogers and Ames [4]. In 2007, Mason and Maluleke [5] introduced the Lie point symmetry into this area and investigated the nonlinear radial oscillations of a transversely isotropic incompressible cylindrical tube subjected to time dependent net applied surface pressures; moreover, they proved that for radial and tangential transversely isotropic tubes the differential equations may be reduced to the Abel equations of the second kind. In addition, with the development of the mathematical theory, Yuan et al. [6] investigated the dynamic inflation problems for infinitely long cylindrical tubes composed of a class of transversely isotropic incompressible Ogden materials from the equation itself and discussed the influences of material parameters, structure parameter and applied pressures on the dynamic behaviors of the tubes in detail. Ren [7] studied the dynamical responses, such as motion and destruction of hyperelastic cylindrical shells subjected to dynamic loads on the inner surface. Other references on the dynamic responses for hyperelastic cylindrical structures may be found in Dai and Kong [8], Yuan et al. [9], and so on.

The purpose of this paper is to investigate the nonlinear periodic oscillation of a cylindrical microvoid centered at an infinitely long cylinder, where the cylinder is composed of an isotropic incompressible Ogden material [10] and its outer surface is subjected to a uniform radial tensile load. In Section 2, the basic governing equations, the boundary conditions and the initial conditions are presented. In Section 3, a second order nonlinear ordinary differential equation describing the motion of the microvoid is obtained. Then, in Section 4, some nonlinear dynamic analyses of the equation are performed in detail. Meanwhile, some numerical examples are given.

2. Mathematical Model

The mathematical model examined in this paper is listed as follows.

(a) Basic Governing Equations In the absence of body force, the equilibrium differential equation, the incompressibility condition and the strain-energy function associated with the known Ogden material are given by

(2.1)
(2.2)
(2.3)

(b) Boundary Conditions and Initial Conditions The boundary conditions are given by

(2.4)

The initial conditions are as follows:

(2.5)

In (2.1)~(2.5), σi(r, t) = λi(∂W/∂λi) − p(r, t), i = r, θ are the principal Cauchy stresses, p(r, t) is the hydrostatic pressure related to the incompressibility condition, λr = ∂r/∂R, λθ = r/R are the radial and the circumference stretches, respectively, r = r(R, t), 0 < A ≤ R ≤ B is the radial deformation function with time to be determined, and A and B are the radius of the microvoid and the outer radius of the cylinder in the undeformed configuration, respectively. ρ0 is the constant mass density of the material. μi,  αi  (i = 1,2) are material parameters. The boundary conditions in (2.4) mean that the surface of the microvoid is traction free and the outer surface of the cylinder is subjected to a uniform radial tensile load, denoted by p0. The initial conditions in (2.5) mean that the cylinder is in an undeformed state at time t = 0.

3. Solutions

From the incompressibility condition (2.2) we find that
(3.1)
where r1(t) is an undetermined radial motion function of the radius of the microvoid. From (3.1), it is easy to know that the radial motion of the cylinder can be completely described by r1(t).
From (3.1), it is not difficult to show that
(3.2)
Substituting (3.2) into (2.1), integrating it with respect to r from r(A, t) to r(B, t) and using the traction boundary conditions in (2.4), we obtain
(3.3)
where ,  .

Obviously, (3.3) is a second order nonlinear ordinary differential equation with respect to r1(t). Next we study the qualitative properties of solutions of (3.3).

For convenience, we introduce the following dimensionless notations:
(3.4)
Thus, the initial conditions in (2.5) reduce to
(3.5)
and (3.3) may be rewritten as
(3.6)
where
(3.7)

4. Nonlinear Dynamic Analyses

Multiplying (3.6) by , we obtain the following first integral:
(4.1)
where
(4.2)
Attentively, U(x, δ) > 0 is valid for any , which means that (4.1) has real solutions only when V(x, p0, δ) < 0. However, V(x, p0, δ) < 0 is equivalent to . The stationary point of V(x, p0, δ) can be obtained from Vx(x, p0, δ) = 0, this leads to
(4.3)
where P = p0/μ1, μ = μ2/μ1.

Interestingly, the equilibrium points of (3.6) can be determined by the roots of (4.3).

4.1. Influences of Parameters on the Solution of (3.6)

4.1.1. Influences of Material Parameters

The following conclusions can be obtained from (4.3).
  • (i)

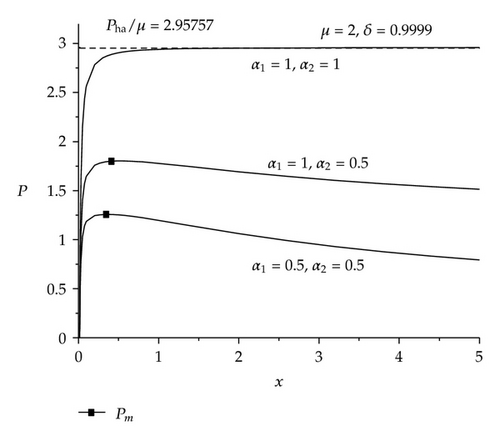
    For the given values of μ and δ, if 0 < α1, α2 < 1, there exists a maximum point, written as (xm, Pm). P increases monotonically as 0 < x < xm and decreases monotonically as x > xm.

  • (ii)

    For the case that α1 = α2 = 1, we have , which means (4.3) has a horizontal asymptote, written as . For the given values of μ and δ, curves of P versus x are shown in Figure 1 for 0 < α1, α2 ≤ 1.

  • (iii)

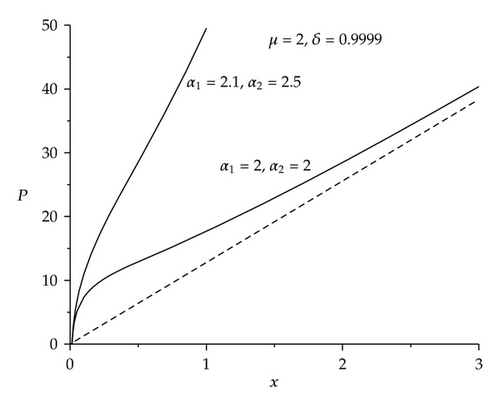
    If α1, α2 > 1, we have lim x→+∞ G(x, δ, α1, α2, μ) = +∞. P increases strictly with the increasing x. Particularly, if α1 = α2 = 2, it is easy to prove that there is another asymptote, written as Pa(x) = −((1 + μ)/2)ln (1 − δ2)x. For the given values of μ and δ, Figure 2 shows the relationships of P versus x for α1, α2 > 1.

  • (iv)

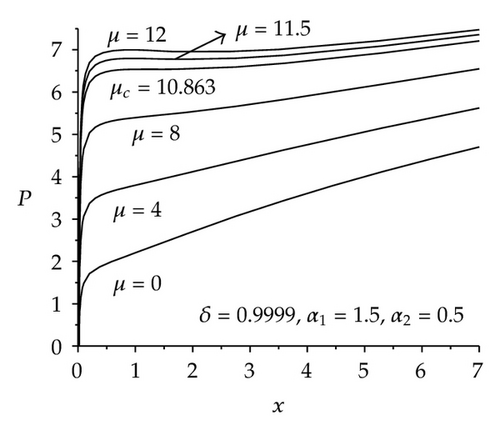
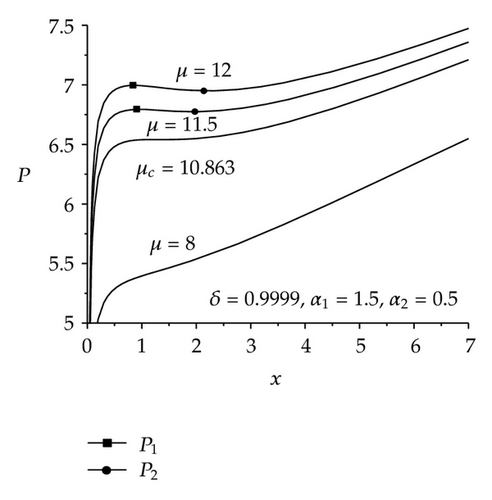
    For the case that α1 > 1, 0 < α2 < 1 or 0 < α1 < 1, α2 > 1 (here, we only discuss the case that α1 > 1, 0 < α2 < 1), it can be proved that there exists a critical value of μ, written as μc, such that P increases monotonically if 0 ≤ μ < μc and has a local maximum and a local minimum if μ > μc, written as P1 and P2, respectively. Curves of P versus x are given in Figure 3 for α1 > 1, 0 < α2 < 1 and for the given values of δ.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Curves of P ~ x for 0 < α1, α2 ≤ 1.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Curves of P ~ x for α1, α2 > 1.
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Curves of P ~ x for α1 > 1, 0 < α2 < 1.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Curves of P ~ x for α1 > 1, 0 < α2 < 1.

4.1.2. Influence of Structure Parameter

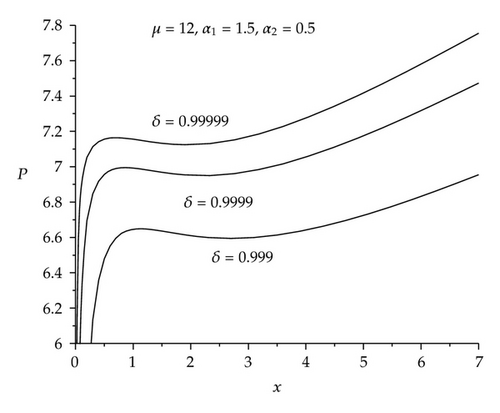
Once the values of α1, α2, and μ are given, the influence of δ on the relationships of P versus x is shown in Figure 4.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Curves of P ~ x for different values of δ.

4.2. Number of Equilibrium Points

  • (1)

    For the case that 0 < α1, α2 < 1, it can be seen from Figure 1 that there are two different roots of (4.3) as 0 < P < Pm, written as x1 and x2 (x1 < x2). It means that (3.6) has two equilibrium points (x1, 0) and (x2, 0); moreover, (x1, 0) is a center and (x2, 0) is a saddle point.

  • (2)

    If α1 = α2 = 1, (3.6) has a unique equilibrium point as 0 ≤ P < Pha, written as (x3, 0); moreover, (x3, 0) is a center. While P > Pha, (3.6) has no equilibrium point.

  • (3)

    For the case that α1, α2 > 1, (3.6) has only one equilibrium point as shown in Figure 2, written as (x4, 0), and it is also a center.

  • (4)

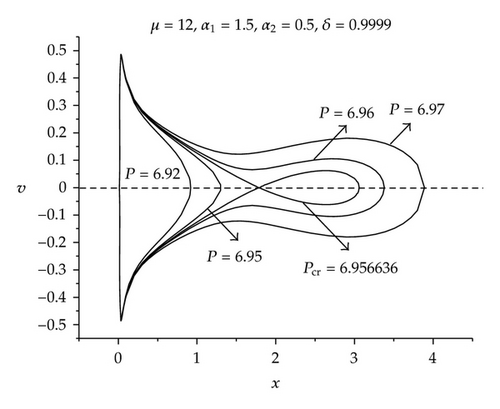
    If α1 > 1, 0 < α2 < 1, from the above analyses we know that P has a local maximum P1 and a local minimum P2 as μ > μc, where μc is a critical value of μ. Equation (3.6) has a unique equilibrium point as P > P1 or P < P2, written as (x5, 0), and it is a center. Equation (3.6) has exactly three equilibrium points as P1 > P > P2, written as (x6, 0), (x7, 0), and (x8, 0), respectively, where x6 < x7 < x8; moreover, (x6, 0) and (x8, 0) are centers and (x7, 0) is a saddle point. For the given values of μ, α1, α2, and δ, the phase diagrams of (4.1) are shown in Figure 5. It is found that the radial oscillation of the microvoid presents a nonlinear periodic oscillation; moreover, the amplitude of the oscillation increases gradually as P increases from 0 to Pcr. However, the increase of the amplitude of the nonlinear periodic oscillation is discontinuous as P passes through Pcr. Another interesting phenomenon occurs as P = Pcr, namely, the phase diagram is a homoclinic orbit at the moment.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Phase diagrams for different values of P and for μ = 12, α1 = 1.5, α2 = 0.5, and δ = 0.9999.

5. Conclusions

In this paper, the nonlinear periodic oscillation of a cylindrical microvoid centered at the isotropic incompressible Ogden cylinder is examined. Some interesting nonlinear dynamic properties of the mathematical model are obtained. The main conclusions are as follows.
  • (1)

    If α1 > 1, 0 < α2 < 1, it is proved that the motion of the microvoid is the nonlinear periodic oscillation for any given load, but there exist some special values of material parameters, the phase diagrams of the motion equation have homoclinic orbits, which means that the amplitude of the nonlinear periodic oscillation increases discontinuously with the increasing load.

  • (2)

    For the case that α1, α2 ≥ 1, the radial oscillation of the microvoid always presents a nonlinear periodic oscillation.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (nos. 10872045, 11232003); the Program for New Century Excellent Talents in University (no. NCET-09-0096); the Fundamental Research Funds for the Central Universities (no. DC12010112); the Program for Liaoning Excellent Talents in University (no. LR2012044).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.