The tracking problem for continuous-time systems is investigated. It is assumed that the states of the systems are not available. An observer is firstly designed to estimate the states by using the ℋ_∞ method. The control action is consist of a state-feedback control, an integral component, and a feedforward loop. The linear-matrix-inequality region is used to constrain the eigenvalue location for the closed-loop systems. The control gains can be obtained by solving a sequence of linear matrix inequalities (LMIs) which can guarantee the mixed ℋ₂/ℋ_∞ performance for the closed-loop systems.

1. Introduction

The tracking control is a fundamental and also the most important control problem no matter from the control theory and from the practical applications [1]. As we know, in industry, the proportional-integral-derivative (PID) controller has greatly dominated the feedback control loops since it was firstly introduced in the 1940s. It was shown in a recent survey that more than 90% of all feedback controllers in use recently were PID controllers, although there are a lot of newly emerging advanced control theories and practical design techniques such as the sliding mode control, the model predictive control, and the robust control [1].

For those newly emerging advanced control theories and practical design techniques, it is obvious that there are some advantages over the traditional PID control. However, PID controllers have simple structures but can provide good tracking performance for the majority of industrial plants, such as chemical processes, motor drives, automotive, bio-mechanical systems, hydraulic systems, and flight vehicles. It is also necessary to mention that it is difficult to tune the PID gains (no theoretical optimal solution). Moreover, there is not an effective algorithm to design the PID controller for multi-input-multi-output systems. However, if we analyze the system in the state-space model, there is not a significant difference between the single-input-single-output systems and multi-input-multi-output systems [2]. It is natural to ask whether we can employ new controller design techniques to design the tracking controller but maintaining the simplicity of the controller structure. Meanwhile, the design scenario is also applicable for the multi-input-multi-output systems.

On another research frontier, the robust control has attracted a lot of attention in the past decades [3, 4]. One of the prominent strengthes of the robust control is that the effect of the external inputs on the controlled output can be attenuated and minimized. For the reference tracking control problem, the external inputs are the tracking reference and the load disturbance. Therefore, it is possible to convert the design problem for the tracking controller to a standard robust controller design problem.

In the robust control, there are mainly three control strategies: (1) ℋ_∞ control which aims to minimize the energy-to-energy gain from the external inputs to the controlled output [5–9]; (2) ℋ₂control which is used to attenuate the controlled output when the external input is a unit white noise [10]; (3) mixed ℋ₂/ℋ_∞ control which considers both performance indexes [11–16]. It is well known that the ℋ_∞ control has been applied to various plants and offers more robust results than the ℋ₂ control. However, the ℋ_∞ control is sensitive to the white noise when the system is subject to a white external disturbance. For the tracking control problem, although the reference and the load disturbance are both taken as the external inputs, they are different from the distribution of the frequencies. Therefore, in order to embrace the advantages of both ℋ_∞ control and ℋ₂ control, it is desired to employ the strategy of the mixed ℋ₂/ℋ_∞ control which was proposed in [11, 12, 17, 18]. It is also necessary to mention that there is another strategy named energy-to-peak control [19, 20]. Actually, the energy-to-peak control can be classified into the ℋ₂ control.

For the sake of improving the transient response, only the feedback loop is insufficient. The feedforward loop is also necessary to contribute into the control law [21–25]. The main contributions of this work can be summarized as follows. (1) The tracking control strategy of the modified PI control is proposed. The integral action is used to eliminate the tracking error. The modified proportional control (observer-based state feedback control) is used to re-assign the eigenvalues of the closed-loop systems. (2) The feedforward control loop is also utilized to further improve the tracking performance. (3) A mixed ℋ₂/ℋ_∞ control framework is proposed to the tracking control problem.

2. Problem Formulation

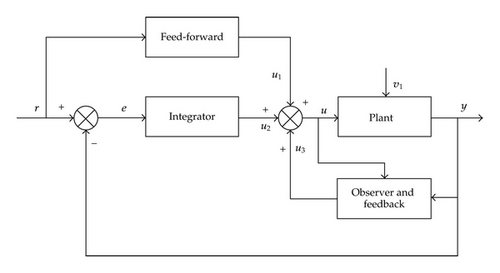
The tracking control scheme used in this paper is illustrated in Figure 1. There are three components in the control action: feed-forward control, integral control, and observer-based state feedback control. The plant is subject to an external disturbance v₁(t) which is assumed to be an energy-bounded signal. In order to stabilize unstable systems, the feedback control loop is a state-feedback control. Since not all the states are available from the measurements, a Luenberger observer is used to estimate the states of the plant by using the contaminated output y(t).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Tracking control scheme for continues-time systems.

Consider the following continuous-time systems:

(2.1)

where x(t) ∈ ℝⁿ denotes the state vector of the system,

represents the control input, y(t) ∈ ℝ^q is the measured output, and

denotes the load disturbance to the plant. The matrices A, B₁, B₂, C, and D are constant with appropriate dimensions.

In the following, we will discuss our main assumptions. Based on these assumptions, we will present the controller design procedure in the following sections.

(1)
The matrix set (A, B₁) is stabilizable and the matrix set (C, A) is detectable.
(2)
The determinant of the matrix exists.
(3)
The output matrix C has full row rank.
(4)
All the external excitations are energy bounded.

In the stabilization and the pole placement, we propose to use the observer-based state-feedback control. The dynamics of Luenberger observer can be represented by

(2.2)

where

has the same dimension as x(t), and K is one parameter to be designed. The design objective of the observer is to choose the parameter K such that the state

can track the state x(t), well. Defining the state-tracking error as

, we have

(2.3)

Here, v(t) = v₁(t) is assumed to be energy bounded.

To deal with another external input r(t) and eliminate the output tracking error, we introduce a new state x_r(t) as

(2.4)

Note that x_r(t) is the integration of the output tracking error. By considering the equations from (2.1) to (2.4), we derive an augmented system as

(2.5)

where

(2.6)

To fulfill the proposed control scheme, the control law used is

(2.7)

where H = diag⁡{I, 0, I}, and L₁ and L₂ are two parameters to be designed. Note that a suitable value for L₁ can place the poles for the closed-loop system such that the system has a good transient response. Substituting the control law into the augmented system (2.5), the dynamics of the closed-loop system is described as

(2.8)

In the tracking control, the tracking error is required to be as smaller as possible. Hence, we utilize the following cost function:

(2.9)

where R is the positive-definite weighting matrix. It is necessary to mention that the cost function can be transformed into the 2-norm of a controlled output:

(2.10)

Here,

(2.11)

In summary, the closed-loop system with the controlled output has the following form:

(2.12)

It is important to emphasize that there are two external inputs w_∞(t) and w₂(t) in the closed-loop system in (2.12). In order to constrain the impact of these two excitations, we introduce the following control objectives for the closed-loop system:

(2.13)

where

is the 2-norm of the transfer function from w₂(t) to z(t) and

is the infinity norm of the transfer function from w_∞(t) to z(t). In addition, to obtain a suitable transient response of the closed-loop system, it is required to place the poles into a specific region. More specifically, the following issues are to be dealt with.

(Q₁) To design the observer and the feedback controller that the poles of the closed-loop system in (2.12) are located in a prescribed region.
(Q₂) To investigate the mixed ℋ₂/ℋ_∞ performance of the closed-loop system in (2.12) with ℒ₂ bounded w₂(t) and w_∞(t), that is, for given scalars γ > 0 and β > 0, find conditions and design the tracking controller such that

(2.14)

Before ending the section, a useful lemma named Schur complement is introduced.

Lemma 2.1 (Schur complement). Given a symmetric matrix , the following three conditions are identical:

(i)
Ξ < 0;
(ii)
Ξ₁₁ < 0, ;
(iii)
.

3. Main Results

The pole placement in LMI regions with feedback control has attracted increasing attentions since it was originally proposed in [26]. In this paper, we adopt the definition of the LMI region.

Definition 3.1 (LMI region [26]). A subset 𝒟 of the complex plane is called an LMI region if there exists a symmetric matrix Γ and a matrix Π such that

(3.1)

Here,

and the characteristic equation f_𝒟(Z) has the following expression:

(3.2)

where, for a complex Z,

For the closed-loop system in (2.12), the requirement of the stability is fundamental and crucial. Now, we are in a position to introduce the quadratic 𝒟-stability for the closed-loop system.

Definition 3.2 (Quadratical 𝒟-stability [26]). For a given LMI region defined in (2.2), the unforced closed-loop system in (2.12) is said to be quadratically 𝒟-stable if there exists a positive defined matrix P such that

(3.3)

Note that there are external excitations in the closed-loop system. In order to evaluate the impact of the external excitations, we study the mixed ℋ₂/ℋ_∞ performance of the closed-loop system in (2.12) by assuming the parameters of the controller and the observer are known. The following theorem provides the conditions under which the closed-loop system in (2.12) is quadratically 𝒟-stable, , and .

Theorem 3.3. Given two positive scalars β and γ, the closed-loop system in (2.12) is quadratically 𝒟_∞-stable with and if there exists a symmetric matrix P = P^T > 0 satisfying (3.3):

(3.4)

(3.5)

Proof. The condition (3.3) can guarantee the quadratically 𝒟_∞-stability of the closed-loop system in (2.12). In addition, the conditions (3.4) and (3.5) are a special case in [27] with only one vertex.

It is important to emphasize that the parameters to be determined are coupled with the positive-definite matrix P in Theorem 3.3. Thus, Theorem 3.3 cannot directly be used to design the observer and the tracking controller. The main challenge is to decouple the parameters to be determined with the Lyapunov weighting matrix P and derive conditions in LMIs when the observer and the tracking controller are unknown.

In order to deal with the challenge, an ℋ_∞ observer is designed firstly. For the estimation error system (2.3), a controlled output z_e(t) is chosen as the state, that is,

(3.6)

It can be seen from (3.6) that there is an external disturbance exciting the system. To attenuate and minimize the effect of this disturbance, the control strategy of ℋ_∞ control will be employed. The design method is proposed in the following theorem.

Theorem 3.4. Given a positive scalar γ_e, the estimation error system in (3.6) is asymptotically stable with an ℋ_∞ performance index γ_e if there exists a symmetric matrix Q = Q^T > 0 and satisfying

(3.7)

Moreover, the estimation gain K can be calculated by using the formula

Proof. It follows from Theorem 3.3 that the system in (3.6) is asymptotically stable with an ℋ_∞ performance index γ_e if there exists a positive definite matrix Q such that the following condition is satisfied:

(3.8)

Defining a new variable

, the condition (3.7) implies that the inequality (3.8) holds, that is, the system is asymptotically stable and the performance is guaranteed.

Generally, we need to minimize the disturbance attenuation level γ_e. The minimal index γ_e can be obtained by using the following corollary.

Corollary 3.5. The minimum ℋ_∞ performance index γ_e for the estimation error system in (3.6) can be found by solving the following convex optimization problem:

(3.9)

Recalling the conditions in Theorem 3.3, although the observer gain K is calculated by using the proposed ℋ_∞ design in Theorem 3.4, the inequalities (3.3) and (3.5) are still bilinear matrix inequalities which cannot be easily solved due to the NP-hard. As we know, there is not existing effective algorithm which can be applied to solve the bilinear matrix inequalities. In this paper, we propose an approach to transfer the bilinear matrix conditions into linear matrix inequalities and linear matrix equation.

Theorem 3.6. Given two positive scalars β and γ, the closed-loop system in (2.12) is quadratically 𝒟-stable with and if there exist a symmetric matrix P = P^T > 0, G, W = W^T > 0, , and satisfying the following hybrid conditions:

(3.10)

(3.11)

(3.12)

(3.13)

(3.14)

Moreover, the feedback gains L₁ and L₂ can be calculated by the following equations:

(3.15)

Proof. By using the Schur complement, the inequality (3.13) implies

(3.16)

By further considering the condition (3.12), one can conclude that the conditions (3.12) and (3.13) imply that the inequality (3.4) holds.

Since , the bilinear terms and in Theorem 3.3 become and . By defining two new variables and , we can get the rest of conditions in Theorem 3.6 from Theorem 3.3. This proof is completed.

Remark 3.7. It is necessary to point out that there is one matrix equation in Theorem 3.6. The matrix equation cannot be directly solved by the MATLAB LMI toolbox. However, we can further transfer the equation to an approximate inequality as:

(3.17)

where ε is a smaller scalar.

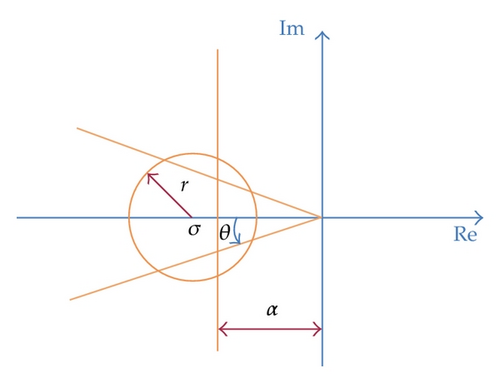
Remark 3.8. It is necessary to show some examples on LMI regions. Generally, there are three types of regions are widely considered.

(1) Vertical Strip As shown in Figure 2, the left-half plane is delimited by a vertical strip Re = −α with a positive α. In this case, the characteristic equation is

(3.18)

with Γ = 2α and Π = 1.

(2) Disk The disk is with the center at (−σ, 0) and with the radius of r. In this case, the characteristic equation is

(3.19)

(3) Conic Sector The conic sector is with the center at the origin and with the inner angle 0 < θ < π/2. In this case, the characteristic equation is

(3.20)

There are two prescribed performance indexes β and γ in Theorem 3.6. For the control problem, it is required that both performance indexes should be as smaller as possible. However, the indexes are conflicting. When the first one is minimized, the second one will increase. When the second one is minimized, the first one will increase. In order to compromise both performance indexes, there are the following three choices for the mixed ℋ₂/ℋ_∞.

Corollary 3.9. For a given ℋ₂ performance index β, the minimum ℋ_∞ performance index γ for the closed-loop system in (2.12) can be found by solving the following convex optimization problem:

(3.21)

Corollary 3.10. For a given ℋ_∞ performance index γ, the minimum ℋ₂ performance index β for the closed-loop system in (2.12) can be found by solving the following convex optimization problem:

(3.22)

Corollary 3.11. The minimum mixed ℋ₂/ℋ_∞ performance index for the closed-loop system in (2.12) can be found by solving the following convex optimization problem:

(3.23)

where ρ is a given weighting scalar.

Design Algorithm The design procedure of the controller is summarized as follows.

Step 1. Derive the dynamics of the control plant or identify the system model of the control plant.

Step 2. Augment the system to an augmented one in the form of (2.5).

Step 3. Choose the weighting factor .

Step 4. Design the estimator gain K by using Theorem 3.4 or Corollary 3.5.

Step 5. Design the gains L₁ and L₂ in the control law by using Corollary 3.9, Corollary 3.10, or Corollary 3.11.

4. Numerical Example

In this section, a numerical example is considered to show the effectiveness of the proposed design method.

Consider the continuous-time system in Figure 1 with the following matrices:

(4.1)

When the γ_e is set to 0.1, the calculated estimator gain is

(4.2)

By employing Corollary 3.9, the gains in the control law are

(4.3)

5. Conclusions

The control problem for continuous-time systems under the framework of ℋ₂/ℋ_∞ control was studied in this work. By using the augmentation technique, the design of observer-based PI control was transferred to the design of an output feedback control. Moreover, the constraint on the eigenvalue location was also incorporated in the design. The parameters can be tuned by solving a set of linear matrix inequalities.

Acknowledgment

This paper is supported by Natural Science Foundation of Zhejiang Proviance of China under Grant no. Y1080112.

References

1 Åström K. J. and Hägglund T., The future of PID control, Control Engineering Practice. (2001) 9, no. 11, 1163–1175.
10.1016/S0967-0661(01)00062-4
Web of Science® Google Scholar
2 Venkataramani R. and Bresler Y., Filter design for MIMO sampling and reconstruction, IEEE Transactions on Signal Processing. (2003) 51, no. 12, 3164–3176, https://doi.org/10.1109/TSP.2003.819002, 2044824.
10.1109/TSP.2003.819002
Web of Science® Google Scholar
3 Gahinet P. and Apkarian P., A linear matrix inequality approach to ℋ_∞ control, International Journal of Robust and Nonlinear Control. (1994) 4, no. 4, 421–448, https://doi.org/10.1002/rnc.4590040403, 1286148, ZBL0808.93024.
10.1002/rnc.4590040403
Web of Science® Google Scholar
4 Pipeleers G., Demeulenaere B., Swevers J., and Vandenberghe L., Extended LMI characterizations for stability and performance of linear systems, Systems & Control Letters. (2009) 58, no. 7, 510–518, https://doi.org/10.1016/j.sysconle.2009.03.001, 2536426, ZBL1166.93014.
10.1016/j.sysconle.2009.03.001
Web of Science® Google Scholar
5 Elsayed A. and Grimble M. J., A new approach to the ℋ_∞ design of optimal digital linear filters, IMA Journal of Mathematical Control and Information. (1989) 6, no. 2, 233–251, https://doi.org/10.1093/imamci/6.2.233, 1003679, ZBL0678.93063.
10.1093/imamci/6.2.233
Web of Science® Google Scholar
6 McEneaney W. M., Robust/ℋ_∞ filtering for nonlinear systems, Systems & Control Letters. (1998) 33, no. 5, 315–325, https://doi.org/10.1016/S0167-6911(97)00124-2, 1623874.
10.1016/S0167-6911(97)00124-2
Web of Science® Google Scholar
7 Apkarian P. and Gahinet P., A convex characterization of gain-scheduled ℋ_∞ controllers, IEEETransactions on Automatic Control. (1995) 40, no. 5, 853–864, https://doi.org/10.1109/9.384219, 1328081, ZBL0826.93028.
10.1109/9.384219
Web of Science® Google Scholar
8 Kim S. H. and Park P., Relaxed H_∞ stabilization conditions for discrete-time fuzzy systems with interval time-varying delays, IEEE Transactions on Fuzzy Systems. (2009) 17, no. 6, 1441–1449.
10.1109/TFUZZ.2009.2028016
Web of Science® Google Scholar
9 Tseng C.-S., A novel approach to ℋ_∞ decentralized fuzzy-observer-based fuzzy control design for nonlinear interconnected systems, IEEE Transactions on Fuzzy Systems. (2008) 16, no. 5, 1337–1350.
10.1109/TFUZZ.2008.924355
Web of Science® Google Scholar
10 Gao H., Meng X., and Chen T., A new design of robust ℋ₂ filters for uncertain systems, Systems & Control Letters. (2008) 57, no. 7, 585–593, https://doi.org/10.1016/j.sysconle.2007.12.008, 2415972, ZBL1140.93043.
10.1016/j.sysconle.2007.12.008
Web of Science® Google Scholar
11 Khargonekar P. P. and Rotea M. A., Mixed ℋ₂/ℋ_∞ control: a convex optimization approach, IEEETransactions on Automatic Control. (1991) 36, no. 7, 824–837, https://doi.org/10.1109/9.85062, 1109820, ZBL0748.93031.
10.1109/9.85062
Web of Science® Google Scholar
12 Limebeer D. J. N., Anderson B. D. O., and Hendel B., A Nash game approach to mixed ℋ₂/ℋ_∞ control, IEEE Transactions on Automatic Control. (1994) 39, no. 1, 69–82, https://doi.org/10.1109/9.273340, 1258676, ZBL0796.93027.
10.1109/9.273340
Web of Science® Google Scholar
13 Lin Y.-C. and Lo J.-C., Robust mixed ℋ₂/ℋ_∞ filtering for time-delay fuzzy systems, IEEE Transactions on Signal Processing. (2006) 54, no. 8, 2897–2909.
10.1109/TSP.2006.875380
Web of Science® Google Scholar
14 Palhares R. M. and Peres P. L. D., LMI approach to the mixed ℋ₂/ℋ_∞ filtering design for discrete-time systems, IEEE Transactions on Aerospace and Electronic Systems. (2001) 37, no. 1, 292–296.
10.1109/7.913689
Web of Science® Google Scholar
15 Khosrowjerdi M.-J., Nikoukhah R., and Safari-Shad N., Fault detection in a mixed ℋ₂/ℋ_∞ setting, Proceedings of the 42nd IEEE Conference Decision and Control, 2003, Maui, Hawaii USA, 1461–1466.
Google Scholar
16 Aliyu M. D. S. and Boukas E. K., Discrete-time mixed ℋ₂/ℋ_∞ nonlinear filtering, Proceedings of the American Control Conference, 2008, Seattle, Wash, USA, 5230–5235.
Google Scholar
17 Haddad W. M., Bernstein D. S., and Mustafa D., Mixed-norm ℋ₂/ℋ_∞ regulation and estimation: the discrete-time case, Systems & Control Letters. (1991) 16, no. 4, 235–247, https://doi.org/10.1016/0167-6911(91)90011-3, 1102209, ZBL0728.93033.
10.1016/0167-6911(91)90011-3
Web of Science® Google Scholar
18 Khargonekar P. P., Rotea M. A., and Baeyens E., Mixed ℋ₂/ℋ_∞ filtering, International Journal of Robust and Nonlinear Control. (1996) 6, no. 4, 313–330, https://doi.org/10.1002/(SICI)1099-1239(199605)6:4<313::AID-RNC235>3.3.CO;2-#, 1404735, ZBL0849.93063.
10.1002/(SICI)1099-1239(199605)6:4<313::AID-RNC235>3.0.CO;2-8
Web of Science® Google Scholar
19 Palhares R. M. and Peres P. L. D., Robust filtering with guaranteed energy-to-peak performance—an LMI approach, Automatica. (2000) 36, no. 6, 851–858, https://doi.org/10.1016/S0005-1098(99)00211-3, 1829185.
10.1016/S0005-1098(99)00211-3
Web of Science® Google Scholar
20 Grigoriadis K. M. and Watson J. T., Reduced-order ℋ_∞ and ℒ₂ − ℒ_∞ filtering via linear matrix inequalities, IEEE Transactions on Aerospace and Electronic Systems. (1997) 33, no. 4, 1326–1338.
10.1109/7.625133
Web of Science® Google Scholar
21 Kojima A. and Ishijima S., ℋ_∞ preview tracking in output feedback setting, International Journal of Robust and Nonlinear Control. (2004) 14, no. 7, 627–641, https://doi.org/10.1002/rnc.897, 2051387, ZBL1057.93012.
10.1002/rnc.897
Web of Science® Google Scholar
22 Gershon E., Shaked U., and Yaesh I., "ℋ_∞ tracking of linear continuous-time systems with stochastic uncertainties and preview, International Journal of Robust and Nonlinear Control. (2004) 14, no. 7, 607–626, https://doi.org/10.1002/rnc.896, 2051386, ZBL1057.93010.
10.1002/rnc.896
Web of Science® Google Scholar
23 Cohen A. and Shaked U., Linear discrete-time ℋ_∞-optimal tracking with preview, IEEETransactions on Automatic Control. (1997) 42, no. 2, 270–276, https://doi.org/10.1109/9.554409, 1438459.
10.1109/9.554409
Web of Science® Google Scholar
24 Takaba K., Robust servomechanism with preview action for polytopic uncertain systems, International Journal of Robust and Nonlinear Control. (2000) 10, no. 2, 101–111, https://doi.org/10.1002/(SICI)1099-1239(200002)10:2<101::AID-RNC465>3.0.CO;2-9, 1740969, ZBL0944.93504.
10.1002/(SICI)1099-1239(200002)10:2<101::AID-RNC465>3.0.CO;2-9
Web of Science® Google Scholar
25 Kojima A. and Ishijima S., LQ preview synthesis: optimal control and worst case analysis, IEEETransactions on Automatic Control. (1999) 44, no. 2, 352–357, https://doi.org/10.1109/9.746265, 1668996, ZBL1056.93643.
10.1109/9.746265
Web of Science® Google Scholar
26 Chilali M. and Gahinet P., ℋ_∞ design with pole placement constraints: an LMI approach, IEEETransactions on Automatic Control. (1996) 41, no. 3, 358–367, https://doi.org/10.1109/9.486637, 1382985, ZBL0857.93048.
10.1109/9.486637
Web of Science® Google Scholar
27 Gao H., Lam J., and Wang C., Mixed H₂/H_∞ filtering for continuous-time polytopic systems: a parameter-dependent approach, Circuits, Systems, and Signal Processing. (2005) 24, no. 6, 689–702, https://doi.org/10.1007/s00034-005-0612-y, 2200925, ZBL1102.94033.
10.1007/s00034-005-0612-y
Web of Science® Google Scholar

All articles

Observer-Based Mixed ℋ₂/ℋ_∞ Tracking Control for Continuous-Time Systems with Integral Action and Pole Placement

Abstract

1. Introduction

2. Problem Formulation

3. Main Results

4. Numerical Example

5. Conclusions

Acknowledgment

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Observer-Based Mixed ℋ2/ℋ∞ Tracking Control for Continuous-Time Systems with Integral Action and Pole Placement

Abstract

1. Introduction

2. Problem Formulation

3. Main Results

4. Numerical Example

5. Conclusions

Acknowledgment

References

Figures

References

Related

Information

Observer-Based Mixed ℋ₂/ℋ_∞ Tracking Control for Continuous-Time Systems with Integral Action and Pole Placement