Preliminary Design of Debris Removal Missions by Means of Simplified Models for Low-Thrust, Many-Revolution Transfers

1. Introduction

One of the most critical issues related to the exploitation of space around the Earth is the threat posed by space debris. Since the beginning of the space era in the late 1950s, an increasing number of man-made, inert objects has been orbiting the Earth. Recent statistics revealed around 15000 trackable objects, for a total of some 6000 tons of material. Some of these objects are simply spent upper stages of launch vehicles, some others are satellites which are no longer active due to failures or to having reached their end of life. Others, however, are the results of past collisions. It is easy to imagine that even a single collision between two objects is likely to generate tens of smaller objects as a result. The outcome of a collision in an already crowded environment could generate a cascade of collisions generating an exponentially increasing volume of space debris. In fact, the debris produced by a collision is itself likely to collide with other objects, thereby producing other debris which will generate further collisions, and so on. This chain reaction, known as the Kessler Syndrome [1], occurs once the rate of generation of debris due to collisions or simple human-driven additions exceeds the natural debris removal rate. According to Kessler et al., this reaction is likely to be ignited once the object density in a certain orbital band reaches a critical point; once started, it will probably render most spacecraft in that orbital band useless within a matter of months or years.

Recent guidelines issued by international spacer regulatory institutions such as the United Nations Committee for the Peaceful Uses of Outer Space (COPUOS) [2] and the Inter-Agency Space Debris Coordination Committee (IADC) [3] prescribe some actions to be followed by national or private agencies putting satellites into orbit in order to mitigate debris growth. For example, it is demanded that every new mission in Low Earth Orbit (LEO) must be planned such that the satellite itself must re-enter in the Earth’s atmosphere within 25 years after the end of the mission. Alternatively, for higher orbits like geostationary orbits, the requirement is for the spacecraft to be placed on a higher graveyard orbit. Measures like these, even if strictly applied (and at the moment compliance with them is on a voluntary basis), are only likely to slow down the accumulation of space debris around the Earth. Therefore, active removal actions will probably be needed in the near future to eliminate at least the most dangerous objects.

There have been various proposals on how to remove inert objects from space. They can be generally classified in two major groups: contactless and with direct physical contact. In the latter category, one can find methods based on some form of docking with or capturing the object. Once the removing spacecraft and the piece of debris are attached, the latter is dragged into a re-entry trajectory or to a graveyard orbit. Technical problems related to the attitude state of motion of the piece of debris and the fragility of appendices and cover material (including paint) make this removal solution complicated. A potentially interesting solution is represented by Project ROGER [4], developed by EADS/Astrium with the support of ESA. Among contactless solutions, one can find what is commonly referred to as the space broom [5]. It entails irradiating the target object with a high-power laser which will induce sublimation of the surface material; the ejecta plume will then generate a low-thrusting acceleration which will slowly degrade the debris’ orbit until it reaches an altitude where atmospheric drag will accelerate its re-entry. Such a technique has the advantage that no physical contact is required, on the other hand, current proposals envisage the use of lasers installed on Earth and beaming through the atmosphere. The beam collimation and thrust time is, therefore, limited and this solution is effective for small-sized objects only. Recent proposals have demonstrated that the use of in-space laser systems might be more interesting even to remove larger objects [6]. Other proposals involve, for example, the use of electrodynamic tethers [7], inflatable balloons [8], which are meant to be lightweight and efficient but require, however, the physical attachment of the device to the target object and are, therefore, of difficult application to existing debris.

A recent idea simultaneously proposed by Bombardelli and Peláez [9], Ruault et al. [10], and JAXA [11] suggested the use of a collimated beam of ions generated by a spacecraft flying in formation with the piece of debris. In this paper, this concept will be called Ion Beam Shepherd (IBS), using the name introduced by Bombardelli and Peláez. The effect of the ion beam is that of producing a thrusting force, equal in magnitude but opposite in direction, on both the IBS and the piece of debris. This force will induce a thrusting acceleration which can be controlled in order to modify the orbit of the piece of debris. A second ion engine is then fired in a direction opposite to the first one in order to keep the IBS spacecraft at a constant distance from the piece of debris. Among the advantages of this concept is the fact that it employs already existing and proven technologies; it does not require any contact with the target, and the fact that a single spacecraft can be used to fetch and deorbit multiple pieces of debris. In [6], one can find a similar concept that uses concentrated solar light instead of ions to generate a thrust and modify the orbit of debris.

Assuming a scenario in which a single IBS needs to de-orbit multiple pieces of debris, one would need to solve an interesting mission design problem: the optimisation of the de-orbit sequence and trajectories for multiple target objects in minimum time and with minimum propellant. In the hypothetical mission scenario which is analysed in this work, it is assumed that a number of pieces of debris have been shortlisted as priority targets due to the threat they pose to satellites operating in LEO. For example, Liou and Johnson [12] propose some criteria to choose the object whose removal will be most effective to mitigate the risk of collisions. They underline that an effective removal strategy must be targeted first to large objects in crowded orbits up to 1500 km. Thus, a removal mission by means of an IBS spacecraft is planned to be launched from the Earth. Its task is that of removing five objects lying on different low Earth orbits. The design of such a mission is a complex optimisation problem, because it requires the computation of multiple low-thrust, many-revolution transfers. Therefore, this work proposes an approach to the fast estimation and optimisation of the cost and time duration of the fetch and de-orbit sequences. In past works, other authors have already proposed approaches to the design of Low-Thrust (LT), many-revolution transfers, based on analytical solutions to an optimal orbit raising problem under the assumption of small eccentricity [13–15] or on averaging techniques [16–18]. This work, proposes a different approach, based on a first-order solution of perturbed Keplerian motion. The approach in this paper aims at capturing the definition and optimisation of the thrusted arcs for each orbit without sacrificing computational speed. The approach can be classified as direct method for trajectory design as it does not derive the necessary conditions for optimality but translates the initial optimal control problem into an NLP problem.

The paper is organised as follows: Section 2 will briefly outline the IBS concept and in particular will outline how to compute the thrusting acceleration generated on a given target object; Section 3 will analyse an hypothetical mission profile for the removal mission and most important, Sections 3.1 and 3.2 will present in detail the proposed trajectory models. Section 4 will then show how the mission design problem can be then translated into as a series of multiobjective optimisation problems which are solved with a stochastic optimiser. The results are then presented and discussed.

2. The Ion Beam Shepherd Spacecraft

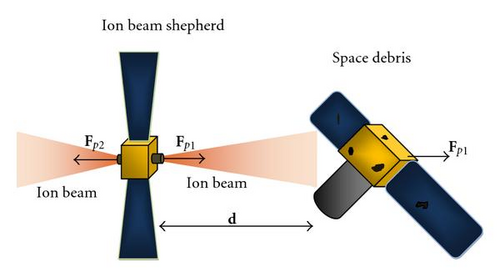
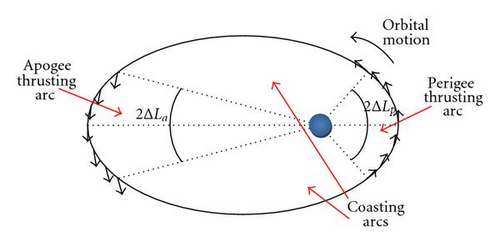
As shown by Bombardelli and Peláez [9], the concept behind the Ion Beam Shepherd is relatively simple and envisions employing a spacecraft provided with two sets of ion engines mounted along the same axis but in opposite directions (see Figure 1). The jet from one of the sets will be directed towards the piece of debris and will exert a thrusting force F_p1 on it. Due to Newton’s third law, an opposite force of same magnitude will also act on the spacecraft itself, but this component will be balanced by the thrust F_p2 provided by the other set of ion engines.

3. Mission Profile

The objective of this study is that of optimising the performance and cost of a debris de-orbiting mission performed by a single spacecraft. As mentioned in the introduction, it is assumed that there are five pieces of debris of different masses and lying in circular orbits with different radii and orientations. It is assumed that the IBS spacecraft departs from a low-Earth parking orbit, rendezvous with the first object, transfers it to an elliptical re-entry orbit, rendezvous with the second object, transfers it to a second elliptical re-entry orbit, and so forth until all five pieces of debris are removed. One important issue is defining in which order the pieces of debris need to be de-orbited. In the following, all possible sequences are generated a priori and optimised one by one.

Given the magnitude of the available thrust acceleration, both phases require a spiral orbit transfer. If a direct transcription approach is used to optimise each spiral the number of parameters that needs to be defined is very high leading to high computational times. The latter fact would make the solution of a multiobjective optimisation of all possible de-orbiting sequences computationally intractable. Thus, in this paper, a simplified, highly efficient, trajectory model is proposed for each one of the two phases.

3.1. De-Orbiting Trajectory Model

The objective of the de-orbiting phase is that of lowering an initial circular orbit such that its perigee is equal or below 300 km, which basically translates into a perigee lowering manoeuvre. Therefore, it is appropriate to assume that in general, as soon as the initial circular orbit becomes slightly eccentric, one keeps thrusting around the apogee in order to lower the perigee. The thrust level will also be kept at its maximum in order to minimize gravity losses. Moreover, since the de-orbit condition is independent of the final orbit’s orientation, one can reasonably assume that the perigee lowering will be performed in-plane. In this sense, the only Keplerian parameters which need to be altered are the semimajor axis and eccentricity. By analysing the structure of Gauss’ variational equations:

$$ (6)

where a is the semimajor axis, e the eccentricity, i the inclination Ω is the Right Ascension of the Ascending node (RAAN), ω the argument of perigee, θ the true anomaly, p the semilatus rectus, and h the angular momentum; a_r,   a_θ, and a_h are the radial, transversal, and out-of-plane components of the thrust acceleration. If one considers the case of thrusting with maximum acceleration along arcs which are symmetrical around apogee (θ = π), one can see that the contributions to semimajor axis and eccentricity variations given by the a_r components are negligible (since they are multiplied by sin  θ). Therefore, a good suboptimal thrust direction can be obtained by imposing a_θ as the only non-zero component of the thrust acceleration. Under these assumptions, the variation of Keplerian parameters will be [20]

$$ (7)

It should be noted that the terms of the variation of ω and θ which depend on a_θ will also be very small due to the presence of sin  θ integrated around θ = π. Figure 2 visualises the proposed pattern for thrusting arcs.

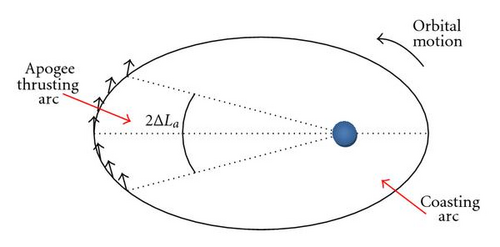
In order to obtain a fast propagation of the thrusting arcs, the analytical propagation of perturbed motion with finite perturbative elements in time (FPET) derived in [19, 21] will be used. In order to employ FPET, one has also to assume that the thrust acceleration is constant around each thrusting arc, which is reasonable given the low propellant consumption per arc. This assumption ensures that, if the engine thrust is constant, the resulting acceleration can also be considered constant over short thrusting arcs.

Motion propagation with FPET is based on a first-order analytical solution of perturbed Keplerian motion. In this formulation, the state is expressed in nonsingular equinoctial elements:

$$ (8)

Assuming constant thrust-acceleration in the radial-transverse reference frame:

$$ (9)

then one can obtain a first-order analytical expansion of the variation of equinoctial elements, parameterised in Longitude L and with respect to a reference longitude L₀:

$$ (10)

where

$$ (11)

where a a₀  P₁₀, P₂₀, Q₁₀, Q₂₀ are reference values at L₀ and a₁, P₁₁, P₂₁, Q₁₁, Q₂₁ are first-order terms as reported in [19, 21]. In [19],it has also been shown that this analytical propagation scheme provides good accuracy along relatively long trajectory arcs.

As explained above, the only nonzero component of the acceleration will be a_θ and since the aim is obtaining a decrease of the orbit energy, it will also be in the negative direction. Therefore, the acceleration azimuth will be α = −π/2 and the elevation β = 0 (since, as already mentioned, the motion will be within the initial orbit plane). The variation of equinoctial elements after an apogee thrusting arc will be given by

$$ (12)

where L_a is the apocentre longitude, L⁻ and L⁺ are the longitudes at the start and end of thrusting, respectively. ΔL_a is the semiamplitude of the apogee thrusting arc. Note that, given that β = 0, there is no variation on Q₁ and Q₂ and thus they are omitted. The coasting time is computed from the last of (10) as

$$ (13)

Since the thrust magnitude and direction are fixed, the only free control parameter is the semiamplitude ΔL_a for each orbit. In order to keep the number of decision variables to a minimum, the semiamplitude for each orbit is computed from a piece-wise linear polynomial interpolating a limited number of ΔL_a,i over a number of orbits. The nodes ΔL_a,i are equally distributed between orbit 1 and an arbitrary number of orbits (in this paper, 1200 was found to be adequate). In this paper, the number of interpolating nodes was limited to 2: ΔL_a1 and ΔL_af.

In order to evaluate the time and ΔV needed to de-orbit a piece of debris from its initial orbit with semimajor axis a_debr0, given a set of decision (or control) parameters ΔL_a1 and ΔL_af, the following procedure was implemented.

• (1)

  Compute the set of initial Equinoctial parameters L₀ and $$, where P₁₀ and P₂₀ will be null due to the fact that the initial orbit is circular.

• (2)

  Initialise the number of orbits, the total ΔV and time of flight to zero:

  $$ (14)

• (3)

  Set E⁻ = E₀ and L_coast = L₀.

• (4)

  Initialise the mass of the IBS spacecraft:

  $$ (15)

• (5)

  While N_orbit is smaller than N_orbitsmax,

  • (a)

    N_orbit = N_orbit + 1.

  • (b)

    Interpolate the amplitude of the thrusting arc in the current orbit, that is, ΔL_a and compute L⁻ = L_a − ΔL_a and L⁺ = L_a + ΔL_a.

  • (c)

    Compute the acceleration ε_IBS−debr acting on the IBS-debris combination from (5).

  • (d)

    Compute the time of flight t_coast spent coasting from L_coast to L⁻.

  • (e)

    Compute the equinoctial parameters after the thrusting arc E⁺ as in (12).

  • (f)

    Compute the current perigee radius r_p and if this is lower than the threshold $$ km proceed to step 6, otherwise, proceed to step g.

  • (g)

    Compute the thrusting time t_thrust from (13) and update the total ΔV cost:

    $$ (16)

  • (h)

    Update the total time of flight:

    $$ (17)

  • (i)

    Update the IBS spacecraft mass:

    $$ (18)

  • (j)

    Set E⁻ = E⁺ and L_coast = L⁺.

• (6)

  Back track the value of the longitude L_f for which $$ and compute the related and t_thrust from (13) and update TOF and ΔV accordingly. Compute the equinoctial parameters E_f at L_f from (12).

At this point, one gets the ΔV, the time of flight TOF, and the semimajor axis and eccentricity of the final orbit (which are easily computed from E_f). It is important to note that, given the simplifications introduced, once one sets the initial mass and orbit of the piece of debris, and the characteristics of the IBS propulsion system, that is, F_tot and I_sp, the de-orbit depends exclusively on the mass of the IBS m_IBS0 at the beginning of the de-orbit phase and the interpolating values for ΔL_a, that is, ΔL_a1 and ΔL_af. Therefore, it was decided to precompute the corresponding ΔV and TOF for a given set of these three parameters and for each piece of debris (i.e., for each m_debr and a_debr0). Table 1 reports upper and lower bounds for m_IBS0, ΔL_a1 and ΔL_af, and the number of samples taken, equally distributed.

Table 1. Bounds and number of samples for the de-orbit parameters.

	mIBS0	ΔLa1	ΔLaf
Lower bound	Mdry + 100 = 350 kg	0	0
Upper bound	Mlaunch = 1000 kg	π	π
Samples	8	50	50

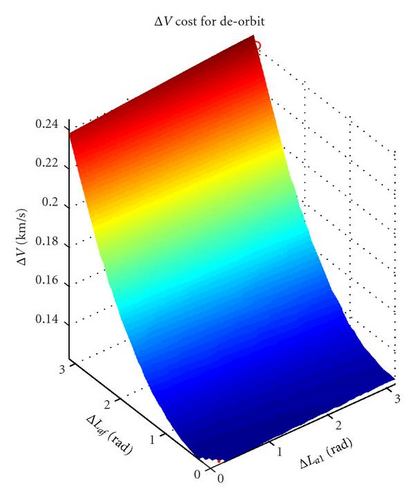
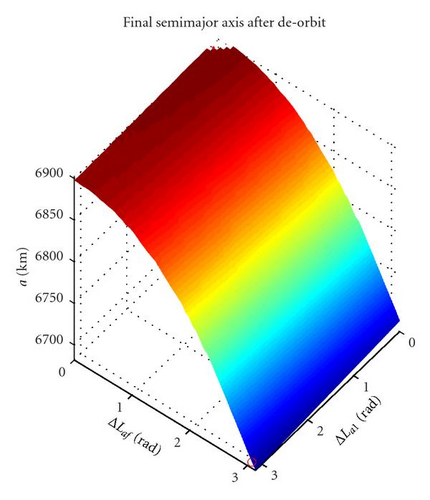
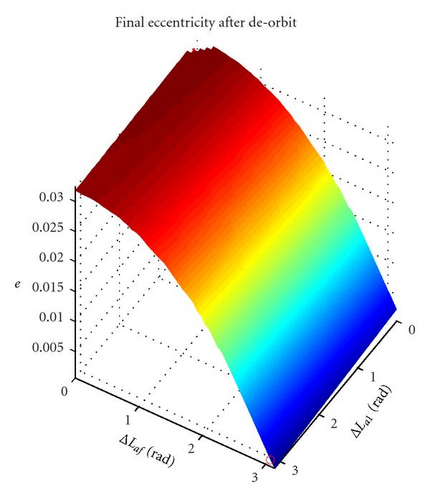
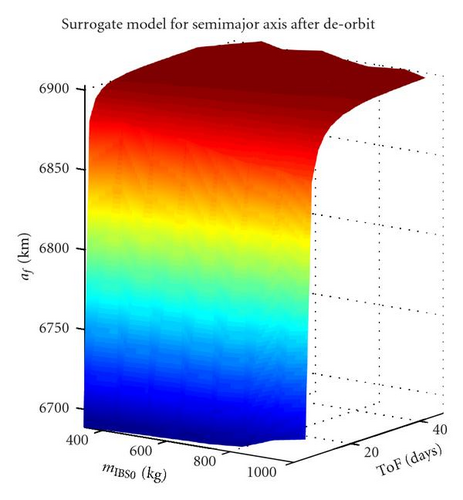
Given the limited number of decision variables, for each piece of debris, one has 20000 de-orbit instances to propagate. Since each instance requires typically 1·10⁻² s of CPU time, with a code implemented in MATLAB and running on a 3.16 GHz, 4 GB desktop PC running Windows 7, the whole computation can be completed in roughly five minutes. The set of de-orbit ΔV and TOF is then used to build a response surface, or surrogate model, of the de-orbiting process. Figures 3(a) and 3(b) show examples of two-dimensional surface, respectively, for ΔV and TOF, with respect to a fixed m_IBS0 of 300 kg. One can see that the two quantities show opposite trends, the ΔV being high when the TOF is low and vice versa. Figures 4(a) and 4(b) show the final semimajor axis and eccentricity, respectively. Note that the minimum TOF transfer corresponds to a quasicircular spiralling trajectory in which the IBS spacecraft is thrusting continuously. On the other hand, the minimum ΔV transfer corresponds also to the one with maximum final eccentricity.

Now, it is desirable that the surrogate model returns the ΔV cost as a function of m_IBS0, m_debr, a_debr0, and TOF. From the available data relating the ΔV and TOF to the decision variables ΔL_a1 and ΔL_af, one can derive the functional relationship between ΔV and TOF. Given a triplet m_IBS0, m_debr, a_debr0, each TOF value defines a level curve on the ΔL_a1 and ΔL_af plane (see Figure 3(a)), which can be mapped into a set of ΔV values (see Figure 3(b)). Within this set, one can take the element with minimum ΔV. Thus, for each time of flight, between a minimum and a maximum, one can derive the corresponding minimum ΔV cost. A similar procedure is followed to find the functional relationship between the final semimajor axis and the TOF. Note that there is no need to do the same for the eccentricity given the fact that the final perigee radius is fixed at $$ and, therefore, the final e can be computed from the final a. In this way one can build the two surrogate models:

$$ (19)

Figures 5(a) and 5(b) show examples of tridimensional plots (m_IBS0-TOF-ΔV and m_IBS0-TOF-a_f, resp.) created by evaluating the surrogated models keeping a_debr0 and m_debr fixed. In Figure 5(a), one can see that there is a large plateau region corresponding to large time of flights and a smaller region close to the minimum TOF where the de-orbit cost increases very steeply and the final semimajor axis in Figure 5(b) similarly decreases. The complete procedure for the creation of the interpolated de-orbit cost models requires few minutes of CPU time and once completed allows for a very fast estimation of the de-orbit cost. The surrogated models will be extremely useful in the multiobjective optimisation of debris removal sequences as it will be shown in the following sections.

3.2. Orbit Transfer Model

According to the scenario presented in Section 3, after having left the debris on a re-entry orbit, the IBS will have to transfer to the orbit of the next debris and rendezvous with it. The design of such a transfer arc would normally require the solution of a fixed-time two point boundary value problem (TPBVP) which would be computationally very expensive given the high number of control parameters and constraints involved. A second simplified model was then created to quickly estimate the cost of a low-thrust multirevolution orbit transfer with boundary constraints. The approach and assumptions presented in this section are similar to those already introduced for the de-orbit model.

First, given the limited acceleration provided by low-thrust propulsion systems, one should consider that the orbit transfer will require a high number of multiple revolutions around the Earth, typical in the range of hundreds to few thousands. In this sense, it is possible to argue that achieving the proper phasing to transfer from the initial to final orbit would not be a major issue. Even a small variation of ω and θ per revolution would be sufficient to attain the required orientation to rendezvous with the piece of debris. Moreover, it is important to bear in mind that, in order to de-orbit the previous debris in the sequence, the IBS spacecraft, started from a circular orbit which was subsequently modified into an elliptical one with perigee $$. Thus, it would be also possible to conveniently adjust the start point of the de-orbit procedure from the circular orbit in order to obtain the proper phasing once this is completed. For all these reasons, it is assumed that in this particular case, the phasing problem will have a negligible effect on the ΔV and time required to rendezvous with the next piece of debris in the sequence. Therefore, in the following, it is assumed that it is not necessary to match the arrival ω and θ computed with the simplified model with those of the target object. Matching the target inclination i and RAAN Ω, instead, cannot be ignored without introducing a considerable error in the ΔV cost. In order to match the inclination and RAAN difference, one need to take into account only the geometric angle between planes of the initial and final orbits, which is given by

$$ (20)

Thus, in order to account for Δi, the inclination of the initial orbit is fictitiously set to zero, while the final one is set at Δi. The matching of the RAAN is assured by performing the circularisation properly. The assumption is that the deorbiting of one piece of debris starts at a true anomaly such that the resulting elliptical orbit has the line of apses perpendicular with the line of the nodes of the following piece of debris. Since the orbits of the debris are assumed to be circular, it is always possible to start the deorbiting at the right true anomaly with minimum delay. This hypothesis will be discussed in more detail with some numerical examples in Section 4.

With these assumptions, the main issue in designing the multirevolution transfer will be that of achieving the required change in the apogee and perigee radii in order to match those of the final orbit, and to achieve the required rotation of the orbit plane.

The control of eccentricity and semimajor axis, required to match the target perigee and apogee altitudes, can be obtained by inserting two thrust arcs per revolution, one around the apogee and one around the perigee. This methodology is analogous to what was done in the previous section for the perigee lowering. In the same way, the radial component of the thrust acceleration is set to zero. The transverse component this time can have either positive or negative sign (α = ±π/2) depending whether the perigee (or apogee) needs to be raised or lowered.

Since a plane change is required, the out-of-plane component of the thrust acceleration is nonzero. Thanks to this, the control parameters can be reduced to the semiamplitude of the apogee and perigee thrusting arcs, ΔL_a and ΔL_p, the sign of the θ component of the thrust acceleration (i.e., the sign of α_a, α_p = ±π/2), and the out-of-plane component in the same arcs, β_a and β_p. Define ΔL_thrust as half the total thrusting arc length and r_t as the ratio of ΔL_thrust which is devoted to apogee thrusting. In order to have a parameterisation which accounts also for the sign of α_a and α_p, the following one is proposed:

$$ (21)

with

$$ (22)

To define the actual values of ΔL_thrust and r_t in each revolution, an interpolating strategy from a set of nodal values similar to the one used for the de-orbit model is adopted. In this case, however, the interpolated values will not be computed with respect to the current revolution number but with respect to the time. Again the number of interpolating nodes can be chosen arbitrarily and is set to 2 in this case, ΔL_t1, ΔL_tf, r_t1, r_tf. For β_a and β_p, it is chosen to have a constant value along the entire transfer. The thrusting pattern along each revolution is shown in Figure 6.

Given a set of control parameters [ΔL_t1 ΔL_tf r_t1 r_tf β_a β_p], a multirevolution transfer with specified duration $$, departing from an orbit defined by $$ and targeted to an orbit defined by $$, is propagated according to the following procedure.

• (1)

  Compute the set of initial Equinoctial parameters L₀ and $$. Q₁₀ and Q₂₀ will be zero since the initial inclination is arbitrarily set to zero.

• (2)

  Compute the set of target Equinoctial parameters $$. Note that $$ and $$ will be zero since in this case the target orbit is a circular one.

• (3)

  Initialise the total ΔV and Time of flight to zero:

  $$ (23)

• (4)

  Set $$ and L_coast,a = L₀.

• (5)

  Initialise the mass of the IBS spacecraft:

  $$ (24)

• (6)

  While $$.

  • (a)

    Compute the interpolated values for ΔL_t and r_t. Hence, calculate α_a, α_p, ΔL_a, and ΔL_p from (21).

  • (b)

    Compute

    $$ (25)

  • (c)

    Compute the current acceleration acting on the spacecraft:

    $$ (26)

  • (d)

    Compute the time of flight t_coast,p spent coasting before perigee from L_coast,p to $$.

  • (e)

    Compute the Equinoctial parameters after the thrusting perigee arc $$ with an expression analogous to (12).

  • (f)

    Compute the thrusting time at perigee t_thrust,p from (13). If $$, proceed to step g. Otherwise, break the iterative sequence and go to step 7.

  • (g)

    Update ΔV and TOF:

    $$ (27)

  • (h)

    Update the IBS spacecraft mass:

    $$ (28)

  • (i)

    Set $$ and $$.

  • (j)

    Compute the current acceleration on the spacecraft:

    $$ (29)

  • (k)

    Compute the time of flight t_coast,a spent coasting before apogee from L_coast,a to $$.

  • (l)

    Compute the equinoctial parameters after the thrusting apogee arc $$ as in (12).

  • (m)

    Compute the thrusting time at apogee t_thrust,a from (13). If $$, proceed to step n. Otherwise, break the iterative sequence and go to step 7.

  • (n)

    Update ΔV and TOF:

    $$ (30)

  • (o)

    Update the IBS spacecraft mass:

    $$ (31)

  • (p)

    Set $$ and $$.

• (7)

  Back-track the point at which $$ and compute the corresponding equinoctial parameters $$ and update ΔV accordingly.

• (8)

  Compute the mismatch between the actual final conditions and the target orbit:

  $$ (32)

Summarizing, the TPBVP has been reduced to an optimisation problem in the form:

$$ (33)

This problem can be solved with a gradient-based optimisation algorithm like MATLAB’s fmincon. Note that the time of flight $$ is specified a priori and, therefore, it might occur that this duration is too short as to obtain the change in the orbital parameters specified by the boundary constraints. In this case, the problem is infeasible and the optimisation is terminated after a maximum of 50 iterations if the constraints are not satisfied.

In the following, an example of transfer from an elliptical orbit with 300 km perigee altitude and eccentricity 0.031 (corresponding to the final orbit of a de-orbiting strategy) to a circular orbit of 1100 km altitude (corresponding to the orbit of the next debris in an hypothetical removal sequence). Parameters of the two orbits are reported in Table 2. Note that the total plane rotation Δi in this case is 10 degrees. The specified time of flight is 70 days.

Table 2. Parameters of departure and arrival orbits.

	a (km)	e	i (deg)
Departure	6892.24	0.031	0
Arrival	7478.16	0	10

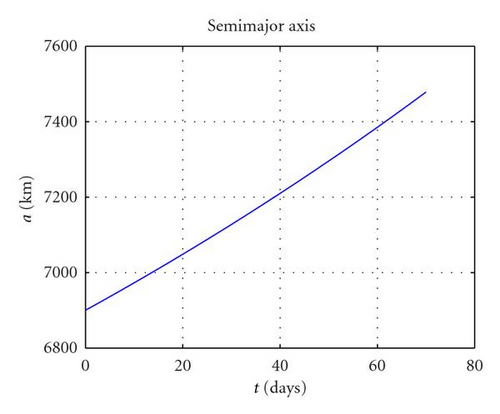
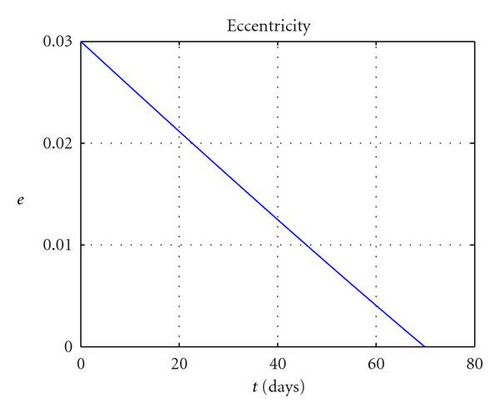
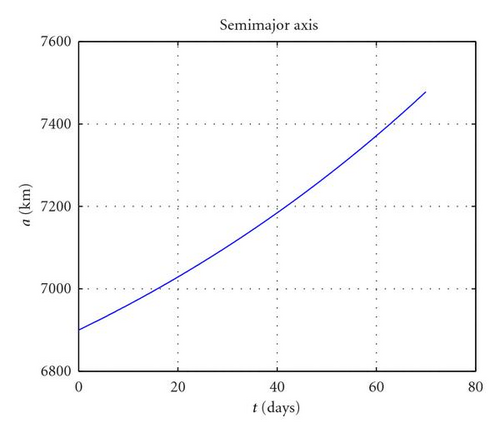
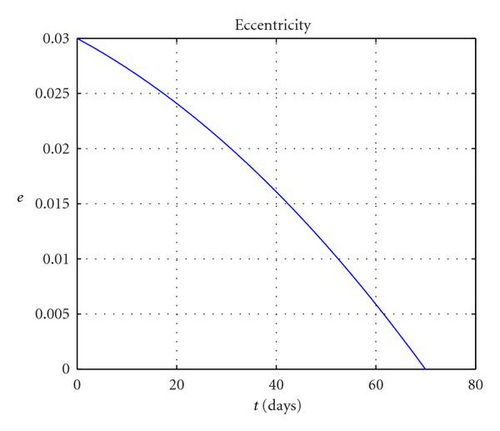
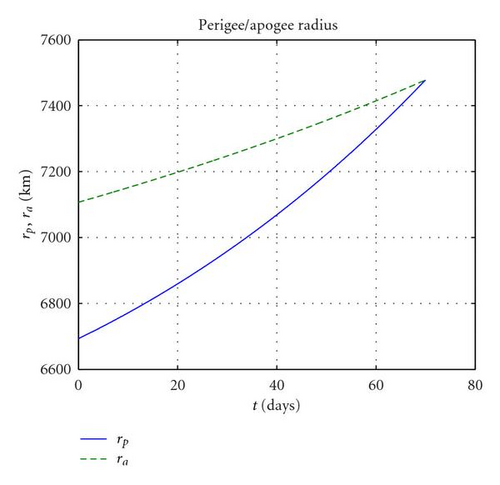
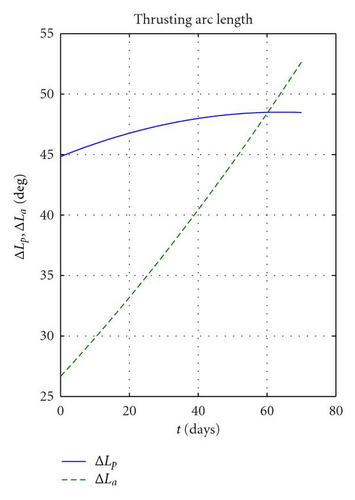
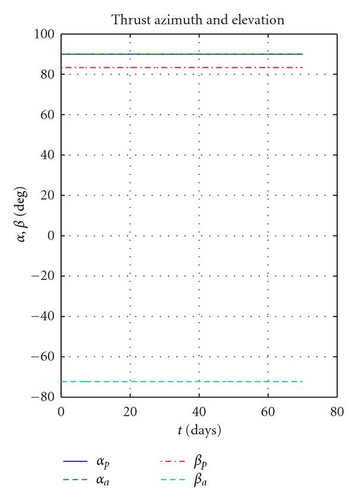
First, it is considered the case of a coplanar transfer, that is, Δi = 0 will be computed. The optimisation problem was solved with fmincon in 6 iterations and less than 10 seconds, returning a minimum ΔV cost of 0.301 km/s, with 1001 revolutions. Figures 7(a)–7(c) report, respectively, the variation of semimajor axis, eccentricity, apogee and perigee radii. One can see that a is monotonically increasing while e on the other hand is monotonically decreasing to zero. In order to reach the desired circular orbit, the perigee had to be raised by almost 700 km while the apogee had to be raised by some 400 km. This higher effort needed to raise the perigee explains the larger amplitude of apogee thrusting arcs ΔL_a compared to perigee ones ΔL_p (as shown in Figure 8(a)). The azimuth thrust angles α_p, α_a (see Figure 8(b)) are both positive since both the perigee and apogee are raised. β_p and β_a are obviously zero because the transfer is coplanar and thus Δi is constantly null.

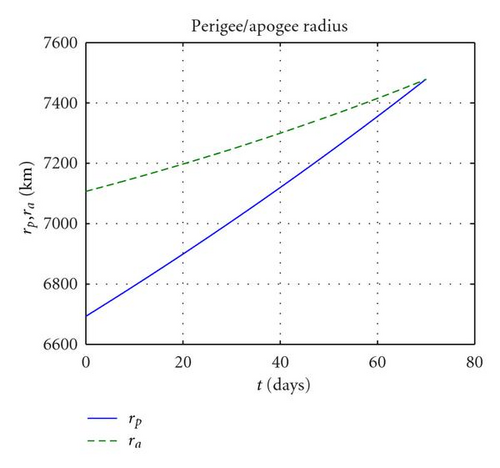
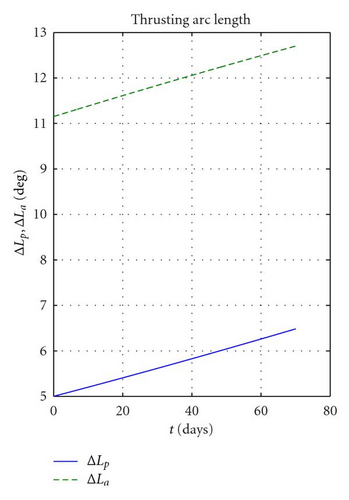
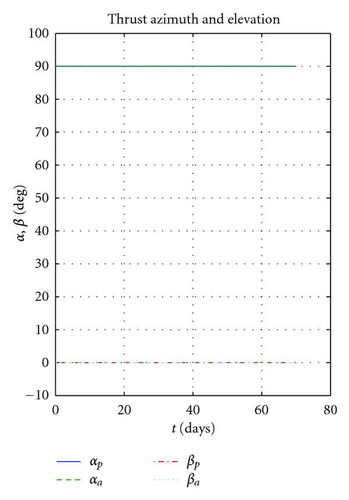
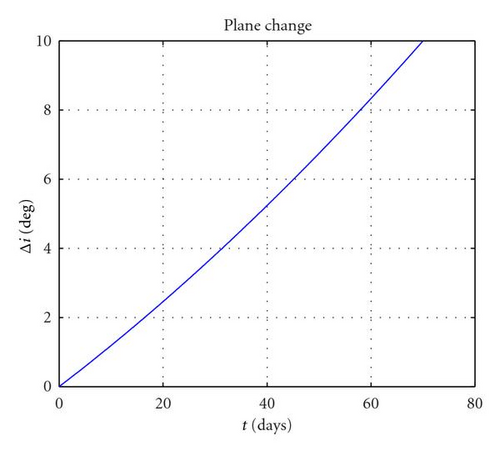
The same problem, but this time with the 10° plane change specified in Table 2, returns a ΔV of 1.480 km/s with 1004 revolutions. The high cost of out plane manoeuvres is well exemplified by the fact that the ΔV required is more than four times larger than a coplanar transfer. As can be seen in Figures 9(a), 9(b), and 9(d), semimajor axis, eccentricity, apogee, and perigee radii show a similar behaviour to the coplanar case while this time also the inclination (as in Figure 9(c)) increases monotonically to 10 degrees. By analysing the control parameters in Figure 10(a) one can see that this time the amplitude of the perigee arcs is in general larger than the apogee ones, even if, like in the coplanar case, the increase in perigee is much larger than that of the apogee. This fact is explained by the fact that the out-of-plane component at perigee β_p is close to 90° (see Figure 10(b)), meaning that the thrusting action at perigee is mostly devoted to the plane change. In contrast, β_a is smaller in magnitude, around −70° (the opposite sign is due to the fact that it is advantageous to invert the out-of-plane component twice per revolution), therefore, with a higher in plane component devoted to perigee raising.

4. Multiobjective Optimisation

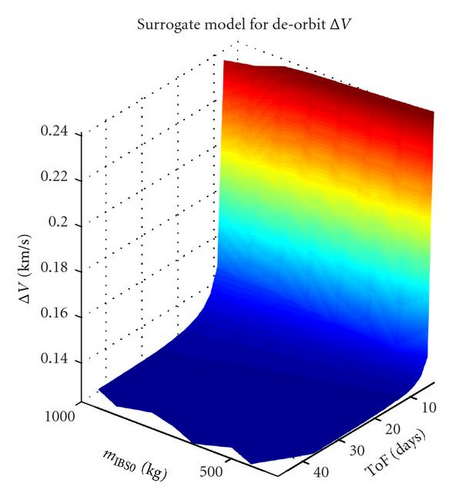
The aim is now that of optimising the timing and sequence of a removal mission by means of a single IBS spacecraft. It is assumed that the spacecraft departs from an LEO with a 250 km semi-major axis altitude and coplanar with respect to the first piece of debris in the sequence. The five target objects have the orbital parameters and mass reported in Table 3. The mass and orbital parameters have been chosen arbitrarily while adhering to the observations in [9, 12] that the most dangerous debris are located in LEO and generally weigh a few hundred kilos. Different values for i and Ω are also taken in order to consider the fact that the pieces of debris, in principle, will be orbiting on different planes. Note that T_Do,min has been computed with the procedure detailed in Section 3.1, and therefore, depends on the characteristics of the IBS spacecraft. Moreover, it is also important to remark that these are only best case figures values which were computed with a minimum hypothetical wet mass of 350 kg (much lower than the actual launch mass of 1000 kg). The surrogate models in (19) can in general consider wet masses between 350 kg and 1000 kg, as shown, for example in Figures 5(a) and 5(b).

Table 4 reports the relative inclination change between the orbit planes of the 5 different objects, as computed from (20).

The domain D is defined by the upper and lower boundaries defined in Table 5. Note that the lower boundaries for de-orbit time are set according to the sequence and the minimum times reported in Table 3.

Each biobjective optimisation problem is solved with MACS, a hybrid-memetic stochastic optimisation algorithm [22]. MACS was run for 40000 function evaluations with 30 agents. Each of the 120 optimisation instances required roughly 6 days of computational time to complete. The outputs are represented by the Pareto optimal solutions w.r.t. ΔV_Tot and ToF_Tot. Figure 11 to Figure 15 collect the Pareto fronts according to the number of the first object in the sequence, that is, the first index in the vector ord, as introduced in (34). In each figure, each colour represents the Pareto front corresponding to one of the 24 debris removal sequences starting with the same object. For example, Figure 11 includes the Pareto fronts of sequences 12345, 13245, 14235, 15234, 12435, and so forth.

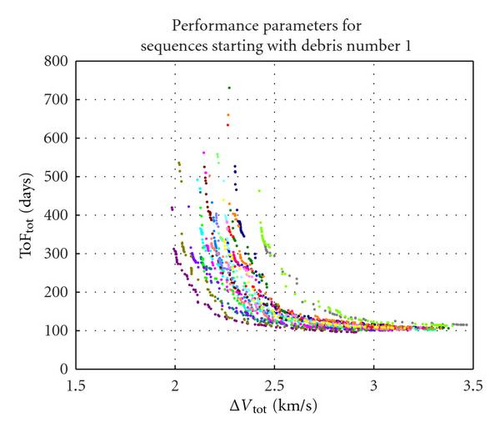
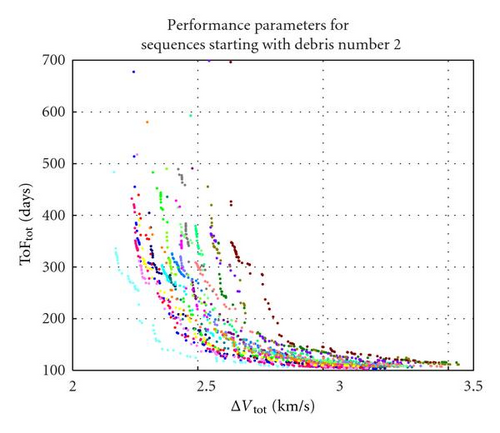
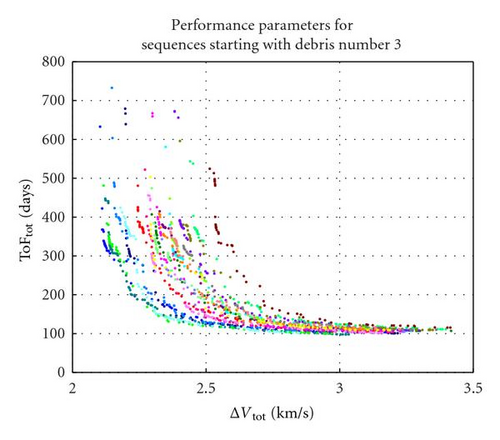
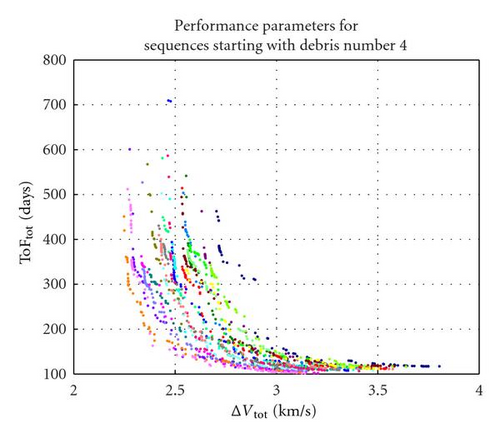
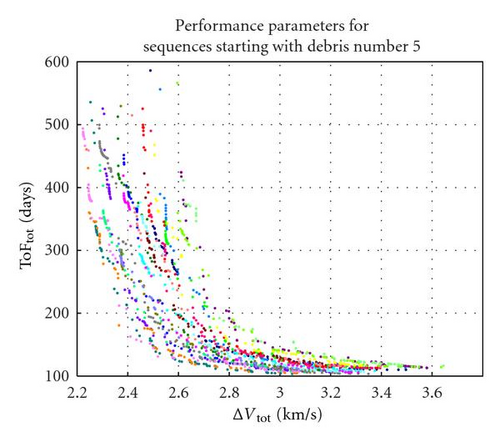
From a visual inspection of the fronts, it is possible to see that sequences starting from debris number 1 seem to present the best ΔV_Tot-TOF_Tot combination, since for most of them the ΔV cost is comprised between 2 and 2.5 km/s. The corresponding times of flight are comprised roughly between 100 and 500 days. The sequences starting with debris nr. 3 and nr. 2 also have a good ΔV while those starting with nr. 4 and nr. 5 appear to be worst. By combining all the partial Pareto fronts, one obtains the globally optimal solutions, as reported in Figure 16.

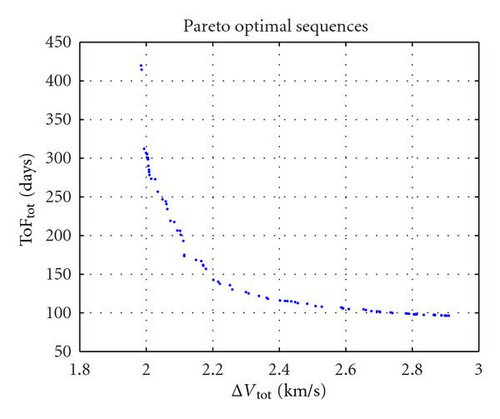
Conv is given by averaging the distance of each point of PF_ord from the closest point of PF_g. The closest PF_ord is to PF_g and the lower Conv will be. Table 6 reports the ranking of the sequences according to Conv.

As one would expect, sequence 13452 has the lowest Conv since it coincides with part of the global Pareto front. Sequences 13524, 13542 and 12543 have also a low Conv index and thus they are quite close to the globally optimal solution, as shown in Figure 17. In general, as already noted before, there is a strong dependence of the quality of the sequence from its first element. One can see that the first ranks are occupied mostly by sequences starting with debris nr. 1 and 3, while those with nr. 4 and 5 have highest Conv and, therefore, occupy predominantly the worst ones. Those starting with nr. 2 are somewhat in the middle. The fact that solutions with nr. 1 and 3 are privileged as first elements in the sequence might be explained from the fact that they lie in the two lowest orbits (see Table 3), and therefore, are easier to reach (please keep in mind that for the rendezvous with the first debris there is no plane change since it is assumed to depart from a coplanar orbit). Another interesting observation is that the best sequences tend to avoid the largest plane changes. For example, in 13452 the plane changes are 1.47°, 2.52°, 1°, and 2°. On the contrary, in the worst one according to Conv, that is, 32415, they are 3.63°, 2.65°, 1.95°, and 1°.

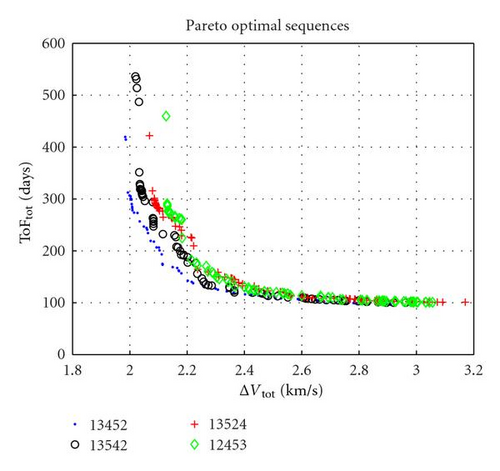
Table 7 reports the minimum values for the performance parameters associated to each sequence, that is, the extreme points of the Pareto fronts. Similar considerations to those made previously also apply to this case, with best values given by sequences starting with nr. 1 and 3 and the worst ones with nr. 4 and 5.

Table 8 shows details about the best V_Tot solution, with sequence 13452. Note that, in general, the ΔV cost of each phase is relatively low, thus leading to the minimum total cost of 1.98 km/s. Correspondingly, their duration is long, meaning that slow but more efficient transfers are preferred. This behaviour is also confirmed by the fact that the de-orbit conditions have nonnegligible eccentricities, which means also that the amplitude of the apogee thrusting arcs during de-orbit (see Figure 2) is kept to a minimum. In this way, propellant is devoted to lowering the perigee only with minimum variation of the apogee altitude.

By analysing in more detail the ΔV cost breakdown, one can see, for example, that the highest figures 0.476 km/s are given by the rendezvous with debris nr. 4 from the de-orbit conditions of debris nr. 3. This high value is justified by the fact that reaching the final orbit radius of 7478.16 requires an apogee raise of 501 km from 6977 km and a perigee raise of 800 km from 6678 km. At the same time, there is also a rotation of the orbit plane of 2.52°. By comparison, the rendezvous with nr. 5 after the de-orbit of nr. 4 is comparatively cheaper even if the radius of the target orbit is still high. In this case, the perigee raise is 500 km while the apogee on the other hand needs to be lowered by 252 km from 7430 km since piece of debris nr. 4 is released on a relatively eccentric orbit with e = 0.053. Plane rotation in this case is only 1°.

Table 9 reports details about the minimum ToF_Tot solution, again with sequence 13452. In contrast to what has been remarked for the previous case, here obviously the duration of each phase is kept to a minimum. For example, values for de-orbit times are very close to the minima reported in Table 3. Conversely, ΔV costs are higher than those in Table 8. Moreover, one can see that the de-orbit trajectories are quasicircular, which suggests that the thrusting arcs are not restricted to apogee passages but cover almost entirely each revolution (i.e., with reference to Figure 2, L_a ≈ 180°).

By applying the above strategies to the minimum ΔV and minimum time of flight sequences, we can obtain a worst-case estimation of the additional time introduced by phasing. The maximum delay introduced by the apses alignment in both cases would be 0.14 days. For the minimum time of flight case in Table 9 (i.e., quasicircular sequence), the worst-case delay due to Δϕ is 2.68 days, leading to a total delay of 2.82 days. This value equates to a 2.93% increase compared to the nominal time of flight of 96.35 days, which can be considered acceptable for a preliminary study. On the contrary, in the case of minimum time of flight sequence as in Table 8, the delay due to Δϕ would be 4.58 days, and the total delay 4.72 days, corresponding to a 1.12% increase on the nominal time of flight of 419.79 days. For these reasons, neglecting the phasing appears to be an acceptable approximation in this preliminary study.

5. Conclusions

This work presented a novel computational approach for the preliminary design of multispiral trajectories. The approach was applied to the design of an orbit debris removal mission by means of an IBS spacecraft. The models proposed here for the computation of low-thrust many-revolution transfers, allowed for a considerable reduction in control parameters and at the same time for a fast propagation of low-thrust motions thanks to the analytical propagation with FPET. Thanks to the reduced computational cost for the evaluation of a single fetch and deorbit operation, a multiobjective optimisation problem could be solved in which thousands of different debris removal sequences were examined to find the optimal ones with respect to ΔV cost and total removal duration. As a result, a considerable number of optimal candidate solutions were found. Analysis of the results showed that the particular removal sequence 13452 is globally optimal. A ranking criterion was proposed to grade all the candidate sequences and identify those that are suboptimal. From the analysis, it was found that there is a dependency of the quality of the sequence on the first target object. Among the open issues for future developments, there is, for example, the possibility of integrating the problem of the sequence choice directly into a single multi-objective optimisation instance, thus obtaining a mixed continuous and discrete optimisation problem. This can be crucial when missions with more than 5–10 debris are considered since the decomposition in fixed-sequence continuous optimisation problems becomes less computationally tractable.

Future work will deal with comparing the proposed approach with similar methods like orbit averaging. In addition, although the proposed method has been applied to the special case of a debris removal mission, it is suitable to be extended and applied to more general trajectory design problems which involve many-revolution transfers from elliptical to circular or from elliptical to elliptical orbits. Current developments are incorporating gravity perturbations in the analytical solution to allow the computation of more accurate solutions.