Journal of Applied Mathematics
Volume 2012, Issue 1 761242
Research Article
Open Access

A Discontinuous Finite Volume Method for the Darcy-Stokes Equations

Zhe Yin, 

Corresponding Author

Zhe Yin

School of Mathematical Sciences, Shandong Normal University, Jinan, Shandong 250014, China sdnu.edu.cn

Search for more papers by this author
Ziwen Jiang, 

Ziwen Jiang

School of Mathematical Sciences, Shandong Normal University, Jinan, Shandong 250014, China sdnu.edu.cn

Search for more papers by this author
Qiang Xu, 

Qiang Xu

School of Mathematical Sciences, Shandong Normal University, Jinan, Shandong 250014, China sdnu.edu.cn

Search for more papers by this author
First published: 27 December 2012
https://doi.org/10.1155/2012/761242
Citations: 3
Academic Editor: Claudio Padra

Abstract

This paper proposes a discontinuous finite volume method for the Darcy-Stokes equations. An optimal error estimate for the approximation of velocity is obtained in a mesh-dependent norm. First-order L2-error estimates are derived for the approximations of both velocity and pressure. Some numerical examples verifying the theoretical predictions are presented.

1. Introduction

The study of discontinuous Galerkin methods has been a very active research field since they were proposed by Reed and Hill [1] in 1973. Discontinuous Galerkin methods use discontinuous functions as finite element approximation and enforce the connections of the approximate solutions between elements by adding some penalty terms. The flexibility of discontinuous functions gives discontinuous Galerkin methods many advantages, such as high parallelizability and localizability. Arnold et al. [2] provided a framework for the analysis of a large class of discontinuous Galerkin methods for second-order elliptic problems.

Based on the advantages of using discontinuous functions for approximation in discontinuous Galerkin methods, it is natural to consider using discontinuous functions as trial functions in the finite volume method, which is called the discontinuous finite volume method. Such a method has the flexibility of the discontinuous Galerkin method and the simplicity and conservative properties of the finite volume method. Ye [3] developed a new discontinuous finite volume method and analyzed it for the second-order elliptic problem. Bi and Geng [4] proposed the semidiscrete and the backward Euler fully discrete discontinuous finite volume element methods for the second-order parabolic problems. Ye [5] considered the discontinuous finite volume method for solving the Stokes problems on both triangular and rectangular meshes and derived an optimal order error estimate for the approximation of velocity in a mesh-dependent norm and first-order L2-error estimates for the approximations of both velocity and pressure.

The Darcy-Stokes problem is interesting for a variety of reasons. Apart from being a modeling tool in its own right, it also appears, less obviously, in time-stepping methods for Stokes and for high Reynolds number flows (where of course the convective term causes additional difficulties). In [6], the nonconforming Crouzeix-Raviart element is stabilized for the Darcy-Stokes problem with terms motivated by a discontinuous Galerkin approach. In [7], a new stabilized mixed finite element method is presented for the Darcy-Stokes equations.

In this paper, we will extend the discontinuous finite volume methods to solve the Darcy-Stokes equations. In our methods, velocity is approximated by discontinuous piecewise linear functions on triangular meshes and by discontinuous piecewise rotated bilinear functions on rectangular meshes. Piecewise constant functions are used as the test functions for velocity in the discontinuous finite volume methods. We obtained an optimal error estimate for the approximation of velocity in a mesh-dependent norm. First-order L2-error estimates are derived for the approximations of both velocity and pressure. For the sake of simplicity and easy presentation of the main ideas of our method, we restrict ourselves to the model problem.

We consider the Darcy-Stokes equations
(1.1a)
(1.1b)
(1.1c)
where Ω is a bounded polygonal domain in R2 with boundary ∂Ω. u = (u1, u2) is the velocity, p is the pressure, and f is a given force term. We assume σ = 1,   μ = 1.

2. Discontinuous Finite Volume Formulation

Let ℛh be a triangular or rectangular partition of Ω. The triangles or rectangles in ℛh are divided into three or four subtriangles by connecting the barycenter of the triangle or the center of the rectangles to their corner nodes, respectively. Then we define the dual partition 𝒯h of the primal partition ℛh to be the union of the triangles shown in Figures 1 and 2 for both triangular and rectangular meshes.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Element T ∈ 𝒯h for triangular mesh.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Element T ∈ 𝒯h for rectangular mesh.
Let Pk(T) consist of all the polynomials with degree less than or equal to k defined on T. We define the finite dimensional trial function space for velocity on a triangular partition by
(2.1)
and on rectangular partition by
(2.2)
where denotes the space of functions of the form on K.
Let Qh be the finite dimensional space for pressure
(2.3)
where
(2.4)
Define the finite dimensional test function space Wh for velocity associated with the dual partition 𝒯h as
(2.5)
Multiplying (1.1a) and (1.1b) by ξ ∈ Wh and q ∈ Qh, respectively, we have
(2.6)
where n is the unit outward normal vector on ∂T.
Let Tj ∈ 𝒯h  (j = 1, …, t) be the triangles in K ∈ ℛh, where t = 3 for triangular meshes and t = 4 for rectangular meshes, as shown as Figures 3 and 4. Then we have
(2.7)
where At+1 = A1.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Triangular partition and its dual.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Rectangular partition and its dual.
For vectors v = (v1, v2) and n = (n1, n2), let v ⊗ n denote the matrix whose ijth component is vi · nj as in [5]. For two matrix valued variables σ and τ, we define . Let . Let e be an interior edge shared by two elements K1 and K2 in ℛh. We define the average {·} and jump [·] on e for scalar q, vector w, and matrix τ, respectively. If e ∈ Γ0,
(2.8)
where n1 and n2 are unit normal vectors on e pointing exterior to K1 and K2, respectively. We also define a matrix valued jump ⟦·⟧ for a vector w as
(2.9)
If e ∈ ∂Ω, define
(2.10)
A straightforward computation gives
(2.11)
(2.12)
Let . Using (2.7), (2.12), and the fact that [∇u] = 0 for on Γ0, (2.7) becomes
(2.13)
Since [p] = 0 for p ∈ H1(Ω) on Γ0, we also have
(2.14)
Let . Define a mapping γ : V(h) → Wh,
(2.15)
where he is the length of the edge e.
We define two norms for V(h) as follows:
(2.16)
where ,  ,, and hK = diameter of K.
As in [5], the standard inverse inequality implies that there is a constant C such that
(2.17)

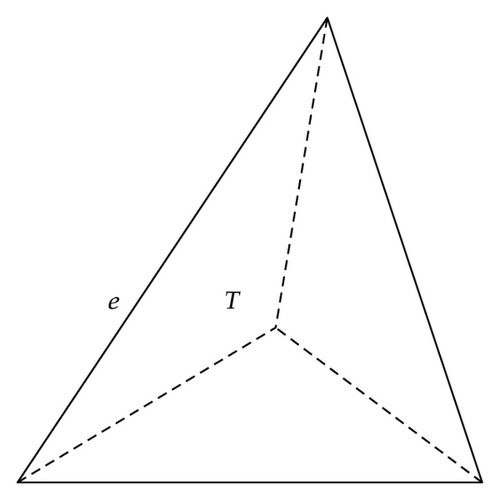
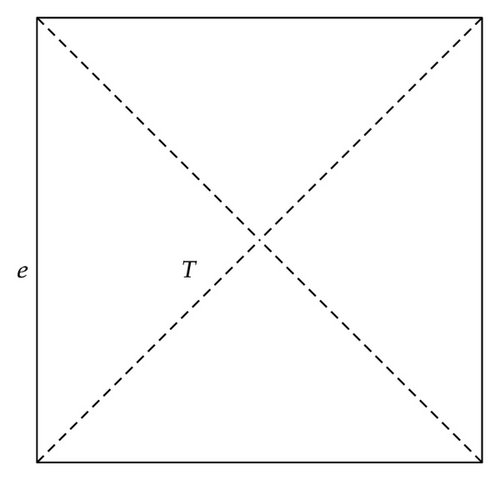
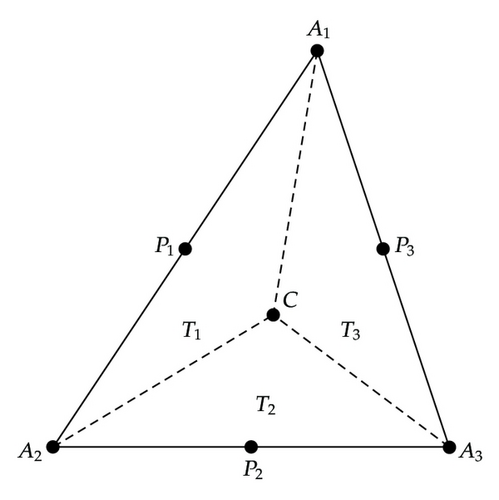
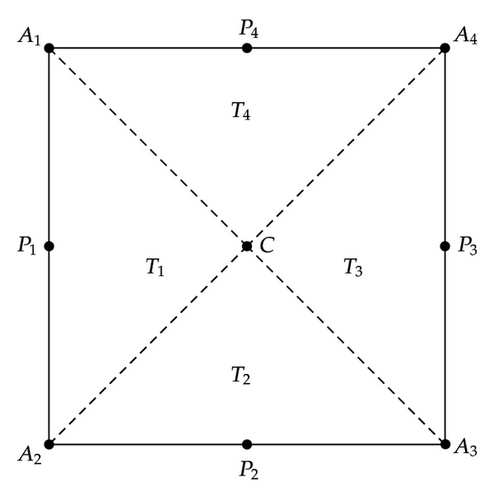
Lemma 2.1. There exists a positive constant C independent of h such that

(2.18)

Proof. As in [4],

(2.19)
where . Since ∥|v∥|1,h ≤ ∥|v∥|, we have ∥v∥≤C∥|v∥|. Note that v ∈ Vh is a piecewise linear function, and . By Lemma 3.6 in [4], I2 ≤ C∥v∥2, I3 ≤ C∥v∥2, we have h∥|v∥| ≤ C∥v∥.

Lemma 2.2 (see [4].)The operator γ is self-adjoint with respect to the L2-inner product, (u, γv) = (v, γu),   ∀ u, v ∈ Vh. Define ∥|v∥|0 = (v, γv) 1/2. Then ∥|·∥|0 and ∥·∥ are equivalent; here the equivalence constants are independent of h. And ∥γv∥ = ∥v∥,   ∀ v ∈ Vh.

Let
(2.20)
It is clear that the solutions (u, p) of the Darcy-Stokes equations (1.1a)–(1.1c) satisfy the following:
(2.21)
Define the following bilinear forms:
(2.22)
Then systems (2.21) are equivalent to
(2.23)
We propose two discontinuous finite volume formulations based on modification of the weak formulation (2.23) for Darcy-Stokes problem (1.1a)–(1.1c). Let us introduce the bilinear forms as follows:
(2.24)
where α > 0 is a parameter to be determined later. For the exact solution (u, p) of (1.1a)–(1.1c), we have
(2.25)
Therefore, it follows from (2.23) that
(2.26)
The corresponding discontinuous finite volume scheme seeks (uh, ph) ∈ Vh × Qh, such that
(2.27)
Let e be an edge of element K. It is well known (see [2]) that there exists a constant C such that for any function g ∈ H2(K),
(2.28)
(2.29)
where C depends only on the minimum angle of K.

Let ∇hv and ∇h · v be the functions whose restriction to each element ∀K ∈ ℛh is equal to ∇v and ∇·v, respectively.

Lemma 2.3. For v, w ∈ V(h), there exists a positive constant C independent of h such that

(2.30)

Proof. Let A**(v, w) = (v, γw) + A*(v, w),

(2.31)
By Lemma 3.1 in [5],
(2.32)

Lemma 2.4 (see [5].)For any (v, q) ∈ V(h) × Qh, one has

(2.33)

Lemma 2.5 (see [5].)For , there exists a positive constant M independent of h such that

(2.34)
If (v, q) ∈ Vh × Qh, then
(2.35)

Lemma 2.6. For any v ∈ Vh, there is a constant C0 independent of h such that for α large enough

(2.36)

Proof. Using the proof of Lemmas 3.1 and 3.5 in [5], for v ∈ Vh,

(2.37)
we have
(2.38)
when α is large enough.

The value of α depends on the constant in the inverse inequality. Therefore, the value of α for which A1(·, ·) is coercive is mesh dependent. We introduce a second discontinuous finite volume scheme which is parameter insensitive. Define a bilinear form as follows:
(2.39)
Similar to the bilinear form A1(·, ·), for the exact solution (u, p) of the Darcy-Stokes problem we have
(2.40)
Consequently, the solution of the Darcy-Stokes problem satisfies the following variational equations:
(2.41)
Our second discontinuous finite volume scheme for (1.1a)–(1.1c) seeks (uh, ph) ∈ Vh × Qh, such that
(2.42)
For any value of α > 0, we have
(2.43)
Similarly, we can prove that
(2.44)
Let A(v, w) = A1(v, w) or A(v, w) = A2(v, w). In the rest of the paper, we assume that the following is true:
(2.45)
If A(v, w) = A2(v, w), (2.45) holds for any α > 0. If A(v, w) = A1(v, w), (2.45) holds for only α large enough.

3. Error Estimates

We will derive optimal error estimates for velocity in the norm ∥|·∥| and for pressure in the L2-norm. A first-order error estimate for velocity in L2-norm will be obtained.

Let e be an interior edge shared by two elements K1 and K2 in ℛh. If , we say that v is continuous on e. We say that v is zero at e ∈ ∂Ω if ∫e v ds = 0. Define a subspace of Vh by
(3.1)
for rectangular meshes and by
(3.2)
for triangular mesh.
It has been proven in [8, 9] that the following discrete inf-sup condition is satisfied; that is, there exists a positive constant β0 such that
(3.3)

Lemma 3.1. The bilinear form B(·, ·) satisfies the discrete inf-sup condition

(3.4)
where β is a positive constant independent of the mesh size h.

Proof. For and q ∈ Qh, we have B(v, q) = (∇h · v, q), and ∥|v∥|1 = ∥v∥1,h. By Poincare-Friedrichs ∥v∥1,h ≤ C | v|1,h, with (3.3), and (2.17) we get for any q ∈ Qh

(3.5)
With β = β0/C1, we have proven (3.4).

Define an operator πK : H1(K) → P1(K) or . For all v ∈ H1(K),
(3.6)
where ei,   i = 1, …, t, are the t sides of the element K. t = 3 if K is a triangle and t = 4 if K is a rectangle. It was proven in [8] that
(3.7)
For all , define Π1v = (Π1v1, Π1v2) ∈ Vh by
(3.8)
Using the definition of Π1 and integration by parts, we can show that
(3.9)
The Cauchy-Schwarz inequality implies
(3.10)
Equations (2.28) and (3.8) imply that
(3.11)
The definitions of the norm ∥|·∥|, (3.7), and (3.11) give
(3.12)

Theorem 3.2. Let (uh, ph) ∈ Vh × Qh be the solution of (2.27), and let ) be the solution of (1.1a)–(1.1c). Then there exists a constant C independent of h such that

(3.13)
(3.14)

Proof. Let ε = u − Π1u,   εh = uh − Π1u,   η = p − Π2p,   ηh = ph − Π2p, where Π2 is L2 projection from . Then u − uh = ε − εh,   p − ph = η − ηh. Subtracting (2.26) from (2.27) and using Lemma 2.4, we get error equations

(3.15a)
(3.15b)
By letting v = εh in (3.15a) and q = ηh in (3.15b), the sum of (3.15a) and (3.15b) gives
(3.16)
Thus, it follows from the coercivity (2.45), the boundedness (2.30), (2.44), and (2.34) that
(3.17)
which implies the following:
(3.18)
The previous estimate can be rewritten as
(3.19)
Now using the triangle inequality, (3.7), the definition of Π2, and the inequality mentioned previously, we get
(3.20)
which completes the estimate for the velocity approximation.

Discrete inf-sup condition (3.4), (3.15a), (3.15b), Lemmas 2.5, 2.4, and inverse inequality give

(3.21)
Using the previous inequality and the triangle inequality, we have completed the proof of (3.13).

Using Lemma 2.1, (3.12), and (3.13), we have

(3.22)
Equations (3.22) and (3.7) and the triangle inequality imply (3.14). We have completed the proof.

4. Numerical Experiments

In this section, we present a numerical example for solving the problems (1.1a)–(1.1c) by using the discontinuous finite volume element method presented with (2.27) and (2.42). Let Ω = (0,1)×(0,1), ℛh be the Delaunay triangulation generated by EasyMesh [10] over Ω with mesh size h as shown in Figure 5. We consider the case of σ = 1,   μ = 1, the exact velocity u1(x, y) = −x2(x − 1) 2y(y − 1)(2y − 1),  u2(x, y) = −u1(y, x) and the pressure p(x, y) = (x − 0.5)(y − 0.5). Denote the numerical solution as uh and ph with step hd which is used to generate the mesh data in the EasyMesh input file, and h = max {he : e ∈ Γ}. For α = 2, the numerical results are presented in Tables 1 and 2. It is observed from the tables that the numerical results support our theory.

Table 1. Error behavior for scheme (2.27).
hd h |∥u − uh∥| ∥u − uh∥ ∥p − ph∥
1/8 1.598e − 1   2.082e − 2     3.393e − 4     1.068e − 2   
1/16 8.372e − 2   1.031e − 2  2.0  9.649e − 5  3.5  5.345e − 3  2.0
1/32 3.679e − 2   5.185e − 3  2.0  2.598e − 5  3.7  2.650e − 3  2.0
1/64 1.899e − 2   2.611e − 3  2.0  6.795e − 6  3.8  1.323e − 3  2.0
1/128 9.413e − 3   1.307e − 3  2.0  1.730e − 6  3.9  6.598e − 4  2.0
Table 2. Error behavior for scheme (2.42).
hd h |∥u − uh∥| ∥u − uh∥ ∥p − ph∥
1/8 1.598e − 1   2.071e − 2     3.280e − 4     1.079e − 2   
1/16 8.372e − 2   1.027e − 2  2.0  9.204e − 5  3.5  5.380e − 3  2.0
1/32 3.679e − 2   5.175e − 3  2.0  2.476e − 5  3.7  2.659e − 3  2.0
1/64 1.899e − 2   2.608e − 3  2.0  6.361e − 6  3.8  1.325e − 3  2.0
1/128 9.413e − 3   1.306e − 3  2.0  1.613e − 6  3.9  6.603e − 4  2.0
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Triangular and its dual partition of (0,1)×(0,1).

Acknowledgments

This paper is supported by the Excellent Young and Middle-Aged Scientists Research Fund of Shandong Province (2008BS09026), National Natural Science Foundation of China (11171193), and National Natural Science Foundation of Shandong Province (ZR2011AM016).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.