Journal of Applied Mathematics
Volume 2012, Issue 1 684292
Research Article
Open Access

Stability and Limit Oscillations of a Control Event-Based Sampling Criterion

M. De la Sen, 

Corresponding Author

M. De la Sen

Institute for Research and Development of Processes, University of Basque Country, Campus of Leioa (Bizkaia), Apartado 644, Bilbao, Leioa 48090, Spain ehu.es

Search for more papers by this author
J. C. Soto, 

J. C. Soto

Department of Applied Mathematics, University of Basque Country, Campus of Bilbao (Bizkaia), Apartado 644, Bilbao 48012, Spain ehu.es

Search for more papers by this author
A. Ibeas, 

A. Ibeas

Department of Telecommunications and Systems Engineering, Autonomous University of Barcelona, Bellaterra 08193, Barcelona, Spain uab.es

Search for more papers by this author
First published: 15 June 2012
https://doi.org/10.1155/2012/684292
Citations: 4
Academic Editor: Zhiwei Gao

Abstract

This paper investigates the presence of limit oscillations in an adaptive sampling system. The basic sampling criterion operates in the sense that each next sampling occurs when the absolute difference of the signal amplitude with respect to its currently sampled signal equalizes a prescribed threshold amplitude. The sampling criterion is extended involving a prescribed set of amplitudes. The limit oscillations might be interpreted through the equivalence of the adaptive sampling and hold device with a nonlinear one consisting of a relay with multiple hysteresis whose parameterization is, in general, dependent on the initial conditions of the dynamic system. The performed study is performed on the time domain.

1. Introduction

Nonperiodic sampling theory opens a set of new technical possibilities compared with the classical sampling with periodic sampling period [1–17]. Those possibilities are as follows:
  • (1)

    to adapt the sampled signals to get better performances [1–3, 6, 8, 9, 16]: for instance, if that signal varies rapidly, then the sampling period is made smaller and vice versa. In general, some constraints in terms of bandwidth, stability, and technical requirements related to circuitry or computing should be respected so that the sampling rate has to belong to some appropriate admissibility domain;

  • (2)

    transmission errors from data to results in algebraic problems like controllability, and observability, might be reduced by a judicious selection of the sampling instants when choosing a fixed sampling period. The reason is that the condition number of the matrix defining the problem depends on such a choice and one can convert a one-parameter optimization problem (a fixed sampling period) into a multiple one (the whole set of distinct sampling periods). In particular, the smaller the condition number of the coefficient matrix is, the smaller are the relative transmission errors from the data to the results depending on each particular problem dealt with [13, 14, 16]. The technique might be used by its “ad-hoc” implementation in a great variety of problems like biology measurements, economics, control theory and engineering, [16], statistics, random sampling [18–22];

  • (3)

    to improve the adaptation transients in recursive identification or adaptive control of both classical or hybrid systems by combining the estimation algorithm with the signal adaptation, [2, 3, 9, 16]. Related adaptive sampling techniques can be used in the context of expert systems to improve the performances under supervisory rules (see, e.g., [17] and references therein).

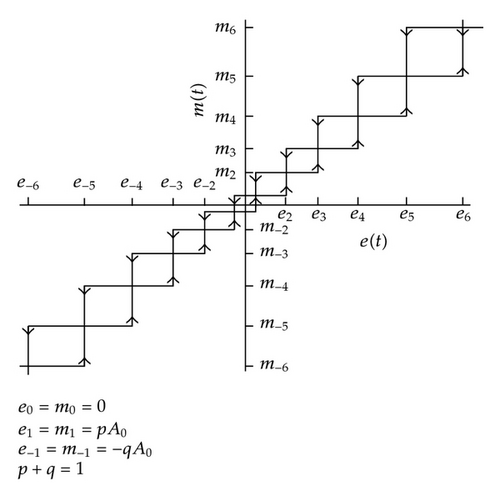
Nonperiodic sampling being updated under certain adaptive sampling laws can often be interpreted as event-driven [23, 24], since, although sampling occurs through time, most of sampling rules involve signal comparison rules related to their immediate previous sampled values or involve certain performance tests. There are a set of background interesting papers, available in the literature, in which sampling is considered either state-dependent, random, or based in stochastic considerations, in general, and used in a number of applications. See, for instance, [19–22, 25–27] and references therein. The constant difference of amplitudes sampling criterion consists of keeping constant the absolute increment of the signal being sampled inbetween each two consecutive sampling instants. The sampling criterion together with its associate sampling and zero-order-hold device is equivalent to a separate nonlinearity which is fully equivalent to a multiple relay with hysteresis (i.e., a multiple bang-bang device with hysteresis). See [1, 15, 18, 28–32] and some references there in. In particular, the sampling criterion based on constant difference of amplitudes was generalized in [1] to the use of several threshold amplitudes the initial sampling criterion proposal of [30] based on a single constant difference of amplitudes. This equivalence motivates that the discretized system exhibits some properties being commonly associated with certain nonlinear systems, like for instance, the potential existence of limit oscillations. A close nonlinear model was proposed in [21] for feedback-based stabilization by triggering the plant output samples through the crossings, with hysteresis, of the signal through its quantization levels. In [22], a close problem related to saturating quantized measurements is focused on. It is well known that limit cycles are highly unsuitable in applications where the objective is to get a zero asymptotic tracking errors. However, they are pursued as an objective for the design of oscillators is some applications as in the design of tank circuits for tuning a suited frequency in radio or TV. There are unified sampling formulations available in the background literature including the presence of sampling constraints in [33, 34] and references there in, and work is also in progress to extend results to the presence of internal delays [35].

This paper characterizes and formalizes mathematically in the time domain the above sampling criterion by extending some previous background results in [1, 18], where the study of oscillations was only approximate and made in a first-harmonic approximation in the frequency domain by using the describing function approach, while the stability properties were not investigated. The results are obtained in the time domain rather than in the frequency one. This allows not to necessarily assume in the problem statement that the linear dynamics exhibits low-pass filtering properties so as to justify the use of a first-harmonic approximation method, as it was done in [1, 15, 18] which was an important limitation in those papers. In this way, such an assumption is no longer needed in the subsequent study which is performed with an exact analytic treatment rather than involving an approximate one. Also, a set of difference amplitudes, rather than a constant fixed one, are allowed in a generalized version of that sampling criterion in order to generalize the problem and to improve its potential applicability. If there is just a single amplitude available to be used as adaptive sampling threshold, then the sampling criterion is referred to as constant amplitude difference sampling criterion (CADSC). If several amplitudes are used, then the sampling criterion is referred to as sampling-dependent amplitude difference sampling criterion (SDADSC). Note that the model obtained in [4] for nonperiodically sampled systems is basically a linear time-varying difference equation. This model is useful to describe discretized systems under varying sampling periods. The time-varying coefficients of the discrete equation depend on both the sequence of sampling periods and the continuous-time parameters. Thus, it may be applied also to the criterion of constant difference of amplitudes. However, some properties like, for instance, the ability of generating limit oscillations are not easily discovered from an earlier inspection when using such a time- varying linear equation. The analysis method for stability and limit oscillations consists basically of the following steps:
  • (a)

    describe the linear uncontrolled continuous-timer system by an ordinary differential equation of nth order submitted to a piecewise constant control input which varies at a set of sampling instants with, in general, time-varying sampling periods. The “ad hoc” control device for this purpose is referred to as a sampling and hold device. The solution of such a differential system is referred to as the “output” of the system;

  • (b)

    discretize the equivalent differential system of nth order at generic sampling instants. Since the input is piecewise constant with discontinuities at such time instants, the solution of the differential equation for any given initial conditions coincides with that of the discretized system at sampling instants. The feedback law for a regulator with unity feedback is introduced so that the piecewise constant feedback control takes the minus values of the output at sampling instants;

  • (c)

    define the generic sampling instants as those generated by the event-driven law of constant absolute difference of amplitudes of the feedback error inbetween each two consecutive sampling instants. This is generalized for a set of prescribed amplitudes in a more general sampling criterion. The amplitude, or the set of amplitudes, parameterize the solution together with the parameters of the continuous-time differential equation. It is seen that the zero-order and hold device together with the sampling criterion is equivalent to a relay with a multiple hysteresis. This suggests that limit cycles of the solution can potentially exist;

  • (d)

    limit cycles are found by investigating double points of the solution in the time domain.

The dynamic system studied in this paper is complex in the sense that a continuous-time dynamic system is controlled by a feedback law consisting of an adaptive sampling criterion which is based on the use of a set of threshold amplitudes to calculate the sequence of sampling instants. For a second-order case study given in Section 5, it is shown that the zero-order hold used for discretization plus the adaptive sampling criterion itself are jointly equivalent to a relay device with multiple hysteresis. The whole feedback type is hybrid since it consist of a continuous-time system under nonlinear feedback and, in this sense, the whole system is a complex dynamic system. The equivalent multiple relay with hysteresis nonlinearity in the feedback-loop allows to interpret the presence of sustained limit oscillations as an asymptotic solution of the state-space trajectory of the closed-loop system.

2. Some Preliminary Framework and Basic Results

Notation 2. R is the set of real numbers, R0+ : = {R∋z ≥ 0} and R+ : = {R∋z > 0} ≡   R0+∖{0}:

  • (i)

    N the set of natural numbers, N0 = N ∪ {0} and is the set of natural numbers ranging from 1 to k;

  • (ii)

    PC(R0+, R) is the set of piecewise continuous functions on R0+;

  • (iii)

    PC(n−1)([0,   Tper]; R) is the set of real almost everywhere piecewise (n − 1)th continuous-time differentiable functions on the definition domain  [0, Tper];

  • (iv)

    In is the nth order identity matrix;

  • (v)

    the disjunction logic rule (spelled “or”) and the conjunction logic rule (spelled “and”) are denoted by the symbols ∨ and ∧, respectively;

  • (vi)

    the ℓ2 (or spectral) vector norm of z ∈ Rq is defined as (with the superscript “T” standing for transposition. The ℓ2-vector norm coincides with the Froebenius or Euclidean vector norm;

  • (vii)

    for a real matrix M ∈ Rp×q, its ℓ2-induced matrix norm is

    ()

  •  

    where σ(MTM) is the spectrum of the square matrix MTM consisting of 1 ≤ nσ ≤ q distinct real eigenvalues λi; . The above positive real maximum defining the spectral ∥M∥2 will be denoted by λmax (MTM). If q = p, then ;

  • (viii)

    f ∈ CT(  Rp × [tk, tk+1);   Rq) is a testing real vector function f :   Rp × [tk, tk+1) → Rq within a testing class CT being of the form f(xτ, τ), where “s” stands for cartesian product of sets, with xτ being a real p-dimensional strip on [tk, tk+1) where tk and tk+1 are two consecutive sampling instants from some sampling criterion SC. Thus, f  is a piecewise real vector function from Rp  to Rq on [tk, tk+  1) valued at some argument vector function x : Rp × [tk, tk+1) → Rq.

Consider the ordinary linear time-invariant differential equation:
()
under a piecewise continuous control input u ∈ PC(R0+, R) to be specified later on, where R0+ : = {R∋z ≥ 0} and the polynomials A(D) and B(D) of real coefficients in the time-derivative operator D : = d/dt (subject to D0 = 1 and Di = DDi−1; for all i ∈ N), which is formally equivalent to the Laplace transform argument “s,” are
()
where a0 ≠ 0, b0 ≠ 0 and n : = deg (A(D)) ≥ m : = deg (B(D)) so that the transfer function G(s) = B(s)/A(s) is realizable, where the Laplace argument “s” is formally equivalent to the time derivative operator “D = d/dt.” It is assumed with no loss in generality that the polynomial A(D) is monic, that is, a0 = 1, since any other nonzero value a0 ≠ 1 can also lead to the differential equation (2.2) after normalization by a0 of all the remaining coefficients of A(D)  and B(D). It is also assumed that any potential zero cancellations in those polynomials, if any, are stable. This guarantees that the state-space realization is either minimal (i.e., no such cancellations exist) or, otherwise, any existing uncontrollable/unobservable mode is stable so that it does not contribute to the asymptotic solution as time tends to infinity. It is well known that the differential equation (2.2) can be described by a nth order differential system of first-order differential equations. Through the paper, it will be assumed that the differential system (2.2)-(2.3) will be controlled by a unity feedback control using, in general, nonperiodically samples y(ti); i ∈ N0 of the solution y(t). The unity feedback control law is from a zero-order sampling and hold device by
()
where r ∈ PC(R0+, R) and e ∈ PC(R0+, R) are, the reference function and the error feedback respectively, and
()
are, the totally ordered set of sampling instants of indicator set ID ⊂ N0  and the associated set of sampling periods with the same indicator set, respectively. Note that u ∈ PC(R0+, R) and it is, in particular, piecewise constant. The following simple sampling process consistency result holds directly from (2.5).

Lemma 2.1. Assume by convention, and with no loss in generality, that the first sampling instant t0 = 0 and that k ∈ N∩ID⇒(k − 1) ∈ ID. Then,

()

The convention t0 = 0 does not imply loss in generality and it is adopted to simplify the exposition. The convention k ∈ N∩ID⇒(k − 1) ∈ ID means that no natural number is missed inbetween any two consecutive ones in the enumeration of the members of SI and SP. The first part of Lemma 2.1 related to means that the sampling process stops in finite time so that there is a maximum and last finite sampling instant and a last unbounded sampling period (therefore, the sequence of sampling periods is unbounded with infinite superior limit), and also that the number of sampling instants and periods is finite. The part of Lemma 2.1 for states that the sampling process never ends so that there are infinitely many sampling instants and periods belonging to their respective numerable sets. Therefore, the cardinal of those sets is denoted by ℵ0 related to infinite cardinals of numerable sets while the ∞ symbol is usually applied to cardinals of nonnumerable sets of infinitely many elements.

2.1. General Sampling Criterion and a Particular Sampling Criterion of Interest

A general sampling criterion SC is defined as an iterative procedure for some given testing function of the error and/or some of its time derivatives on a next tentative sampling period:
()
where t0 ∈ SI. Therefore, given a set of sampling instants tj ∈ SI for all , then tk+1 ∈ SI or Tk = ∞ if the sampling criterion ends such that Card(SI) = k + 1 < ∞. Sampling criteria through testing functions have been obtained in [1–3, 9, 14]. Some of them generate sampling periods in-between consecutive sampling instants as being inversely proportional to the time derivative of the sampled function, or to a combination of consecutive time derivatives, between a maximum admissibility interval (chosen from engineering requirements a such a stability or suited bandwidth). Other types of sampling criteria are chosen through integral criteria over the current sampling period of a quadratic, or some higher even power, of the error time integral between the sampled function and its previous sampled value. A very important one is the so-called criterion of constant difference of amplitudes, firstly proposed in [30], and then generalized formally in [1], and intuitively focused on in [18], to the use of a set of amplitudes which are thresholds of the variation of the sampled signal for each next sampling process. The whole element consisting of the sampling and hold device plus the CADSC (or the more general SDADSC) is, equivalently, modelled with a multiple-hysteresis relay, [1, 15, 18]. This curious nonlinearity in the control law allows an easy interpretation about why sustained oscillations can appear even when the main forward dynamics is linear. If a tracker is being designed, then the use of multiple amplitudes as signal sampling thresholds allows to decrease the amplitude of eventual sustained oscillations and then to improve the tracking servo from a control engineering point of view. Those sampling criteria have the important property, that they are able to generate sustained oscillations of great interest in oscillator design but unsuitable in tracking control problems since a permanent error between the tracked reference and the governed output signals always exists (see also [16, 17, 23]). In particular, some more general sampling criteria are obtained in [17] which include as particular cases many of those ones existing by that date in the background literature. Some of the results in this paper apply to generic sampling criteria (2.7) irrespective of each particular SC. Other specific results are mainly concerned with a particular sampling criterion, the so-called, SDADSC [1], which is defined implicitly as follows:
()
for some given sampling set of amplitude thresholds of the SC. Note from (2.2)–(2.4) that the solution of (2.2) is unique for each set of initial conditions from Picard-Lindelöff theorem for existence and uniqueness of systems of differential equations from continuity and complete induction arguments as follows. Provided that a unique solution exists on [t0, tk) for given initial conditions Diy(0) = y(i)(0) ∈ R, a continuous and time-differentiable solution also exists and it is unique on [t0, tk], and since the input is piecewise constant on [tk, tk+1), it is also continuous and time-differentiable on [tk, tk+1)  for all  tk ∈ SI. Furthermore, the solution is everywhere continuously time-differentiable if n − m ≥ 2. This follows from the uniqueness of the solutions of ordinary differential equations (ODE) for each given set of initial conditions. The following consistency lemma follows. If δk = δ ∈ R+  for all  k ∈ N0  in (2.8), then the sampling criterion becomes, in particular, the CADSC [1].

Lemma 2.2. t0 ∈ SI⇒tk   ∈ SI  for all  k ∈ N, via the sampling rule (2.7), irrespective of the sampling set of amplitudes STδ.

Proof. Proceed by complete induction by assuming that tj ∈ SI for all so that from (2.8):

()

The sampling criterion (2.8) and its particular version for constant amplitude is of major theoretical interest because the study of the dynamics it generates combines properties of discrete-time systems with some properties of nonlinear systems since, in particular, limit cycles appear in the solution of (2.2)–(2.4) for both the SDADSC, [1, 18]. If δk = δ is a positive real constant then the sampling criterion is the CADSC, [1, 15–18]. It has been also used in some practical applications, in particular, for tuning PID controllers, [1]. Since the generation of each next sampling period is given by an implicit function in such sampling criteria, the whole control scheme might be considered in the framework of event-driven processes. It is known that for any nonsingular real matrix  T ∈ Rn×n, a time-differentiable real-state vector function x : R0+ → Rn satisfying may be defined so that (2.2)–(2.4) is equivalent to the nth order dynamic feedback system:
()
where A ∈ Rn×n and b, c ∈ Rn are the matrix of dynamics and the control and output vectors of the continuous-time system, which depend on the coefficients of the polynomials A(D) and B(D) and on the entries to the matrix T, subject to initial conditions at t = 0. Equation (2.10) holds for any set of sampling instants SI independent of the particular sampling criterion (2.7). The solution of the first equation in (2.10) within [tk  , tk+1) yields directly, again irrespective of SC, the following discrete-time system:
()
()
where
()
()
where Φ(Tk) and Ψ(Tk) are the open-loop (i.e., control-free) and closed-loop (i.e., controlled) matrices of dynamics, respectively, and Γ(Tk) and c are the control and output vectors, respectively.

2.2. Basic Stability Results

The global BIBO (bounded-input bounded-output) stability of the controlled closed-loop system is discussed provided that the uncontrolled transfer function: is stable and it possesses a sufficiently small static gain related to the admissible variation domain of the time-varying sampling periods. In the regulation case (i.e., the case of identically zero reference signal r(t)), the closed-loop system is globally asymptotically Lyapunov stable. Note that the static gain of |G(s)|, |G(0)| = |cTA−1b|, varies linearly with |bTc| since det (A) ≠ 0 if A is a stability matrix. Note that the assumption of smallness of the static gain of the open-loop transfer function is always achievable via incorporation of an amplifier of sufficiently small gain K to the forward loop provided that such a condition is not directly satisfied by the given transfer function so that |KcTb| is as sufficiently small as requested. It is proven in the next result that if the maximum allowable time-varying sampling period Tmax  increases, then the allowed |G(0)| being compatible with stability decreases correspondingly. If the minimum allowable sampling period Tmin  increases then such a gain may increase while keeping the stability. The inequality useful for stability in Theorem 2.3 below is , with and . The stability abscissa of the system matrix is also relevant in the sense that the gain is allowed to increase as such an abscissa increases. The subsequent result is concerned with such considerations.

Theorem 2.3. Assume that there is an admissibility bounded interval [Tmin , Tmax ] such that Tk   ∈ [Tmin , Tmax ]  for all  Tk   ∈ SP for some given sampling criterion SC. Assume also that A is a stability matrix (i.e., is a stable transfer function). Then, if |bTc| is sufficiently small according to an explicit trade-off related to the size of [Tmin , Tmax ] and the stability abscissa of the matrix A, then the closed-loop system is BIBO stable. Furthermore, it is globally asymptotically Lyapunov stable in the regulation case without any extra assumptions on the uncontrolled transfer function.

Proof. Direct calculations with (2.12a) and (2.12b) yield:

()
provided that , for some prefixed real constant ε ∈ (0, 1) satisfying , (for some 1 ≤ nσA ≤ n being the number of distinct eigenvalues of A), and Tk ∈ ⌊Tmin , Tmax ⌋for all Tk ∈ SP and any given sampling criterion SC. Proceeding recursively and taking ℓ2-vector and matrix norms in (2.11a) and (2.11b), one gets since
()
()
where , , and then
()
since εk → 0 as k → ∞. Equations (2.11a) and (2.11b)-(2.12a) and (2.12b) are replaced within the inter-sample time intervals with:
()
()
so that, one gets from (2.17)-(2.18) by using (2.15)-(2.16):
()
()
Thus, the dynamic system (2.11a) and (2.11b)-(2.12a) and (2.12b) is bounded-input-bounded-output (BIBO) stable for any uniformly bounded reference r(t). If the reference is identically zero (regulation), then Kr = 0 so that, one gets from (2.16)–(2.20), that lim k→  ∞x(tk + τ) = 0for all  τ ∈ [0, Tk)for all  Tk   ∈ SP, irrespective of the initial conditions so that the dynamic system is globally asymptotically Lyapunov stable. The proof is complete.

It is obvious that Ψ(Tk) is a convergent matrix (i.e., a stability matrix in the discrete sense then all its eigenvalues have modulus less than unity) under the conditions of Theorem 2.3. Note that, otherwise, the state at sampling instants would be at least critically stable and would diverge for certain bounded inputs which could be fixed by construction. Since the system is globally Lyapunov stable then it also exhibits ultimate boundedness in the usual Lyapunov sense as direct conclusion from Theorem 2.3. A more general ultimate boundedness results is now derived without invoking a sufficiently small static gain of the uncontrolled system for a string of consecutive products of the matrix Ψ(Tk) being convergent.

Theorem 2.4. The following properties hold:

  • (i)

    assume that for a given SC and each k ∈ ID, there exists such that , where . Thus, the system is BIBO-stable for any bounded initial state and possesses the ultimate boundedness property for any bounded reference sequence r(tk)for all  tk ∈ SI;

  • (ii)

    if (which holds in particular if for all  tk ∈ SP) and for all    k ∈ N, then the system is BIBO-stable for any bounded initial state.

Proof. For any finite k ∈ ID, define the nonnegative scalar function . Then, for some finite :

()
where
()
with and being independent of k. Now, proceed by contradiction by assuming that is unbounded. Thus, there exists a subsequence which diverges for some numerable subset ID0 of ID so that and . Choose k ∈ ID0 being arbitrarily large but finite, k + i(k) ∈ ID0 so that with Mk being an arbitrarily large positive real number depending on k and ε2 ∈ R+. This is always possible since diverges and 0 ≤ ε1 < 1. From (2.21), one gets:
()
if which leads to a contradiction. As a result, is bounded from above if there exists such that , and the reference sequence is uniformly bounded. Using a similar technique as in Theorem 2.3, it may be proved that the state is bounded within any intersample period on [tk, ∞), for all  k ∈ ID and finite and any sampling criterion SC (i.e., for any tk ∈ SI generated from any SC). Therefore, the system possesses the property of ultimate boundedness. On the other hand, the recursive equations (2.15) lead to a bounded solution sequence on any interval [0, tk) of finite measure if the reference sequence is uniformly bounded since all the matrices of parameters of the discrete-time dynamic system are bounded for finite time irrespective of further considerations. Therefore, ultimate boundedness implies BIBO stability and global stability of the unforced discrete-time system. The proof of Property (i) is complete. Property (ii) follows directly by taking upper bounds via the use of norms in (2.12b).

The following result parallel to Theorem 2.4 is concerned with instability:

Theorem 2.5. Assume that for a given SC and each k ∈ ID, there exists ∞ > i   = i(k) ≥ j ∈   N  such that . Thus, the discrete-time (2.17)-(2.18) system is unstable.

Proof. Take the set of sampling instants tj ∈ SI for the given SC and zero reference input. Now, take initial conditions x(tk) at a finite tk ∈ SI which are a nonzero eigenvector of so that . Then, the system is unstable.

Note that the stability condition in terms of the modulus of eigenvalues being less than unity is equivalent in terms of positive definiteness of the matrix of dynamics to:
()
where 0 ≤ ε0 ≤ ε1 < 1, which could be alternative used in both the statement and proof of Theorem 2.4.

3. Oscillations and Periodic Oscillations

Concerning the discrete-time system (2.17)-(2.18), whose expression at sampling instants are (2.11a) and (2.11b)-(2.12a) and (2.12b) for any sampling criterion SC, the following definitions for weak and strong oscillatory solutions will apply.

Definition 3.1. The discrete-time system (2.11a) and (2.11b)-(2.12a) and (2.12b) has a weak oscillatory output solution for a given sampling criterion SC and some initial conditionx  (0) ∈ Rn if for any given t ∈ R0+, such that y(t) ≠ 0, there exist finite real numbers α(t) ≥ εα and β(t) ≥ εβ, being in general dependent on t, for some εαεβ ∈ R+, such that sign (δy(t, t + α(t))δy(tk,   t + α(t) + β(t))) ≤ 0, where δy(t, t′) : = y(t′) − y(t).

Definition 3.2. The discrete-time system (2.11a) and (2.11b)-(2.12a) and (2.12b) has a strong oscillatory output solution for some initial condition x(0) ∈ Rn if for any given t ∈ R0+, such that y(t) ≠ 0, sign (δy(t, t + α(t))δy(tk, t + α(t) +   β(t))) < 0 and y(t + α(t)) and y(t + α(t) + β(t)) are not both zero.

Definition 3.3. The discrete-time system (2.17)-(2.18) has a periodic weak oscillatory output solution of oscillation period Tper ∈ R+, for some initial condition x(0) ∈ Rn, if sign (δy(t, t + Tper/2)  δy(t, t + Tper)) ≤ 0, y(t, t + Tper) = y(t), for all  t ∈ R+.

Definition 3.4. The discrete-time system (2.17)-(2.18) has a periodic strong oscillatory output solution of oscillation period Tper for some initial condition x  (0) ∈ Rn if it has a periodic weak oscillatory output for such a period and, furthermore, sign(δy(t,   t + Tper/2)δy(t, t + Tper)) < 0 if y(t, t + Tper) = y(t) = 0, for all  t ∈ R+    .

Note that a solution may be oscillatory (Definitions 3.1-3.2) without being periodic (Definitions 3.3-3.4) when there are changes in the sign of the incremental output along intervals of finite duration. A weak oscillation compared to a strong oscillation allows positive or negative increments of the output at finite intervals always of the same sign. The above Definitions 3.1-3.4 might also be refereed to, in general, to nonsymmetric oscillations related to their deviations from zero. Note that trivial solutions, that is, those being identically zero are not periodic solutions according to the given definitions. Note also that periodic solutions can possess an oscillation period which is not the sum of any fixed set of consecutive sampling periods even for such a set obeying a rule implying some repetitive sequence of periods. It turns out that the concepts of oscillation and periodic oscillation may be extended to any of the components of the state vector. The next result establishes clear implications among Definitions 3.1-3.4.

Theorem 3.5. If an output solution is strongly oscillatory, then it is also weakly oscillatory.

If an output solution is strongly periodic oscillatory then it is also weakly periodic oscillatory.

If an output solution is weakly (strongly) periodic oscillatory, then it is also weakly (strongly) oscillatory.

Note that oscillations are not always detectable for any given sampling criterion at arbitrary sampling instants since hidden oscillations can exist which cannot be detected at sampling instants. However, sufficient conditions for existence of oscillations can be formulated at sampling instants as stated in the subsequent results, whose proofs are direct conclusions of Definitions 3.1-3.2.

Theorem 3.6. The discrete-time system (2.11a) and (2.11b)-(2.12a) and (2.12b) exhibits a weak oscillatory output at sampling instants for a given sampling criterion SC and some initial conditionx  (0) ∈ Rn if for any tk ∈ SI, such that y(tk) ≠ 0, there exist finite natural numbers k1(k) and k2(k), being in general dependent on k ∈ ID, such that , where δy(tk, tj) : = y(tj) − y(tk).

Theorem 3.7. The discrete-time system (2.11a) and (2.11b)-(2.12a) and (2.12b) has a strong oscillatory output at sampling instants for some initial condition x(0) ∈ Rn if but and are not both zero.

Remark 3.8. The existence of weak and strong oscillations under the sufficient conditions of Theorems 3.6 and 3.7, respectively, may be investigated explicitly by the use of the state evolution over a finite number of consecutive sampling instants through (2.11b) together with the output expression at sampling instants in the second formula of (2.11a).

Note that the detection of periodic oscillations involving sampling instants only is not feasible even in terms of sufficient-type conditions since the period of such oscillations is not necessarily the exact sum of a consecutive number of limit sampling periods. See, for instance, [1, 15, 16], for SDADSC and CADSC, respectively. The following result states that stable uncontrolled systems which are closed-loop stable under unity feedback, fulfil the conditions of Theorem 2.4 and which do not have stable equilibrium points exhibit oscillatory responses.

Theorem 3.9. Assume that the closed-loop discrete-time system has no stable equilibrium point, while the uncontrolled system is stable under the conditions of Theorem 2.4, and the sampling criterion also fulfils the conditions of Theorem 2.4. Then, any solution of the discrete-time closed-loop system is at least weakly oscillatory and bounded.

Proof. Since any state solution is bounded for bounded initial conditions and do not converge to a constant equilibrium point, it follows that all the state components verify the incremental changes of sign of Definition 4.1, since no one can either converge to a constant or to be unbounded.

A direct related result which follows from Theorem 2.5 is now stated by simple inspection without a formal proof.

Theorem 3.10. Assume that the closed-loop discrete-time system has no stable equilibrium point while the discrete-time system is unstable under the conditions of Theorem 2.5 for some sampling criterion SC. Then, no solution of the discrete-time closed-loop system can be bounded, while it can be weakly oscillatory and unbounded.

Limit cycles are asymptotic isolated limit periodic oscillations in certain nonlinear systems which are usually independent of the initial conditions (as, e.g., the well-known Van der Pol equation). Since some nonlinear systems can also posses oscillations which depend on initial conditions, as for instance, the also well-known Duffing equation modelling certain nonlinear strings with combined linear and cubic effects, no difference is made at the moment between both situations. More precisely, a limit cycle on a plane or a nth-dimensional manifold is a closed trajectory having the property that at least one another trajectory spirals into either as time tends to infinity (stable limit cycles or a self-sustained periodic oscillations) or as time tends to minus infinity (unstable limit cycles). It turns out that a limit cycle exist in the dynamic system of Section 2 only if for a given sampling criterion SC:
()
for some periodic function y* ∈ PC(n−1)([0, Tper]; R) of period Tper > 0 such that:
  • (1)

    all its time derivatives until order (n − 1) exist and are almost everywhere continuous except at the sampling instants;

  • (2)

    Dny*(t) exists everywhere on its definition domain, but it is not required to be continuous in-between sampling instants, so that it is not required for the limit cycle to satisfy y* ∈ PC(n)([0, Tper]; R);

  • (3)

    forall   τ ∈ [0, Tper) such that tk + τ ∉ SI and for if tk+i ∈ SI for some i ∈ N.

4. Limit Oscillations under Sampling Criteria

Note from (2.11a) and (2.11b)-(2.12a) and (2.12b) and (2.17)-(2.18) that for any SC:
()
for all tk ∈ SI, for all τ ∈ ⌊0, Tk+ℓ), for all Tk ∈ SP, and for all k ∈ ID, for all ℓ ∈ N, subject to the parameterizations (2.18) becoming (2.12a) and (2.12b) at sampling instants. If a limit oscillation exists then, one gets for (4.1):
()
for all and some finite p ∈ N0, for some τ ∈ R0+. Thus,
()
where the following limits have to exist for Tk ∈ SP, tk ∈ SI, k ∈ ID, that is, for the sampling periods and sampling instants with a certain repeated string sequence, where in arbitrary starting limit reference sampling instant:
()
Then, the period of the limit oscillation is , some real . A similar limiting equation using (4.2) into the output equation: y(tk+ℓ + τ) = cTx(tk + τ) describes the limit oscillation in the output as tk → ∞. The following four lemmas related to the necessary condition of the existence of a limit cycle independent of a particular SC follow from (4.3)-(4.4) and simple topological considerations about uniqueness of the state- trajectory solution:

Lemma 4.1. If (4.3), subject to (4.4), holds, then ∃  lim t  →  ∞ x(t + τ) = x*(τ) = x*(τ + Tper); for all τ ∈ [0, Tper) and then a limit oscillation of the state-trajectory solution exists.

Proof. Note that and lim k→  ∞ x(tk + τ) = x*(τ) = x*(τ + Tper)    for , for some parameterizing , that is, at a discrete set of (p + 1) limit sampling instants as time tends to infinity, some p   ∈   N0 and this sequence of identities is repeated with period Tper. The statetrajectory inbetween consecutive samples is prescribed according to the values of the limit reference and the state trajectory components cannot intersect at any time so that the periodic limit identity holds in continuous-time as time tends to infinity, and the result is proven.

Lemma 4.2. Assume that distinct double points () exist satisfying (4.3), subject to (4.4) for some p ∈ N0, or equivalently,

()
for all and some τ   ∈   [0, T1). Assume also that if p = 1 then satisfying the above identity is not an equilibrium point. Then, the existing limit oscillation may be tested by any of the double points, in particular, by the limit double point satisfying:
()
If the reference sequence is identically zero, then a limit oscillation exists verifying double points
()

Proof. It follows from (4.3)-(4.4) and Lemma 4.1 since the state-trajectory solution is unique for any initial conditions, sampling periods and reference sequence and a periodic limit oscillation exist. Since the limit double points are distinct, they are not equilibrium points since the state-trajectory solution is unique if p > 1. If p = 1, the double point is not an equilibrium one as a requirement of the lemma statement.

Lemma 4.3. If Lemmas 4.1-4.2 hold for a given set of p ∈ N0 limit sampling periods and some real  τ ∈ [  0,   T1), then there is no other limit oscillation for the same sets of limit sampling periods and limit reference sequence neighboring the one with oscillation period .

Proof. If τ → τ + Δτ then Tper → Tper + Δτ provided identical limit sampling periods . Since all state-trajectories are distinct, any two closed trajectories cannot be everywhere identical. Thus, two trajectories with identical initial conditions should bifurcate to different subtrajectories to complete both distinct closed paths at points inside the common parts of both trajectories. This contradicts the fact that state-trajectory solutions are unique.

Lemma 4.4. All the closed state trajectory solutions verifying Lemmas 4.1–4.3 are either stable or any unstable one, if any, is surrounded by two stable ones, namely, point-wise strictly bounded from above and below by two distinct stable closed state-trajectory solutions. Furthermore, any two closed stable trajectories cannot be arbitrarily close to each other.

Proof. The two matrices have to posses at least to complex conjugate eigenvalues at the unit circumference for both tuples ; ℓ = 1, 2 associated with the limit closed state-trajectory solutions. Otherwise, the system would be either BIBO stable or unstable from Theorems 2.4-2.5. Then, since all the eigenvalues are within the closed unity circle, the system is BIBO stable from Theorem 2.4 so that any state-trajectory solution can be unbounded. Thus, all existing limit oscillations are bounded for all time and then either stable or surrounded by two stable ones. On the other hand, if any two stable trajectories are arbitrary and close to each other then it would be destroyed by any arbitrarily small disturbance so they would not be stable.

Lemma 4.4 dictates that potential limit cycles of the solutions are separated to each other so that there is no accumulation closed attractor of the state-space trajectories. The interpretation of the implications of Lemma 4.4 for a linear dynamics of dimension n = 2 is direct. For n > 2, it is possible to interpret the lemma consequences in a plane corresponding to a 2nd-dimensional system for two of the state components in the same above way while, for the remaining components, we can consider the surrounding trajectories being equal to that one under consideration. The whole surrounding closed trajectories are still distinct from the study for the second-order subsystem.

5. Limit Oscillations for the Constant and Sampling-Dependent Amplitude Difference Sampling Criteria

5.1. The CADSC

The presence of limit oscillations is now discussed for the CADSC from the study of oscillations for sampling criteria in the above section. The conditions of stable limit oscillation for the CADSC are from (4.4)–(4.6) for a double point to exist satisfying:
()
() for some p ∈ N0 and some real ; and, furthermore,
()
for some p1 = p1(ℓ),   p2 = p2(ℓ) ≤ p ∈ N0 and some finite ℓ ∈ N0. Since the limit oscillation may be tested starting at any sampling point, it turns out that any limit oscillation verifying (5.2) for some ℓ ∈ N is also verified 1 ≤ j ≤ ℓ by redefining the integers p1(j); p2(j) ≤ p. A brief intuitive explanation of (5.2) follows. Take any positive value of the limit oscillation for a certain ℓ ∈ N such that (5.1)-(5.2) hold together for some p1(ℓ),   p2(ℓ) ≤   p ∈ N0 for some p ∈ N0 and some real . Then, a limit oscillation with the system output satisfying (5.2) starting with no loss in generality by a positive value, continuing to increase p1 times by step-by-step positive increments δ at each sampling instant, then decreasing p2 times, then increasing again to complete the closed trajectory. Note that for any ℓ ∈ N0 satisfying the given constraints, p = (p − p2(ℓ)) + p2(ℓ) and |p − 2p2(ℓ)| ≤ 2 since the number of negative increments is some p2(ℓ) ≤ p ∈ N0, and the number of positive increments is then p − 2p2(ℓ), while the absolute difference of amplitude increments is of at most two.

5.2. The SDADSC

The study of oscillations can be directly generalized to the SDADSC as follows in the subsequent technical result whose proofs is obvious from (5.1)-(5.2).

Theorem 5.1. (1) Assume that a SDADSC is defined to generate the set of sampling instants SI with a potential set of amplitudes so that ID has a finite cardinal card  ID = γ0 ≥ 1 (If γ0 = 1, one has the particular CADSC);

(2) consider any strictly ordered finite sequence of γ ≥ γ0 amplitudes with possible repetitions;

Let a finite real number M be defined as , where ℓ ∈ N0 is some finite positive integer defined according to δ(ti) = δk ∈ STδfor all  ti ∈ SI and some chosen . Also, define accordingly a set of real numbers and is defined from the given set STδ of amplitudes. If γ > γ0, then contains (γ − γ0) repeated elements.

Thus, if (5.1) is defined with p = j + γ + 1 and (5.2) holds with its right-hand side being replaced with the tuple [  M,   M1, …,   Mγ+1 + τ], then a limit oscillation exists which satisfies the extended version of (5.1) under the above replacements.

Note from Theorem 5.1 that by appropriate choice of the limiting sequence of amplitudes, the amplitudes of sustained oscillations might be reduced compared to the use of a single amplitude.

Example 5.2. First, consider the linear dynamic system of transfer function:

()
where Y(s) and U(s) are the Laplace transforms in the Laplace argument “s” of the output y(t) of a linear time-invariant dynamic system and its time-differentiable control input u(t) under zero initial conditions. Under linear unit control feedback u(t) = −y(t), the closed-loop differential equation becomes y′′(t) + K(y′(t) + y(t)) = 0 subject to any initial conditions y(0) = y0 and y′(0) = y01. Note the following features in the context of limit sustained oscillations:

(1) this system is globally asymptotically stable (then, its solution y(t) is oscillation-free) for any K > 0 and might describe a wide set of real processes, for instance, a mechanical system subject to damping and stiffness or the control of the angular position of a satellite with respect to its axis under a derivative or tachometric control. It can also describe mathematically a linear electric circuit with two energy storing devices specified by capacitors and/or inductors with at least one dissipative device, that is, a resistor which can be in practice either a separated dissipative device or dissipative effects of the inductors/capacitors;

(2) on the other hand, note that, in order to design an electronic oscillator, that is, an electronic system whose asymptotic solution is periodic irrespective of the initial conditions, a nonlinear effect should be included in the system. In this context, note that the solution of the above damped second-order differential equation converges asymptotically to zero for any initial conditions and then it is not periodic so that it cannot be used in that way for the design of oscillators. Note, furthermore, that a typical and well-used class of electric oscillators in applications consists of those being typically synthesized with a saturation function of a certain amplifier linear gain in the linear mode, of saturation threshold and saturated value uM, that is,

()
together with a linear electric network being of at least third order. The oscillation condition at a frequency ω0 is that the first-harmonic of the closed-loop response of the frequency domain satisfies 1 + KG(jω0) = 0, obtained under the replacement s → jω0 with , provided that such an equation has a real solution ω0 > 0. The amplitude of the such a first harmonic is approximately calculated from the companion complex identity , where is the critical locus (i.e., the minus describing function −(sat u(t))/y(t), an extended concept of the frequency response for certain separable or analytical nonlinearities, [36]) which is real for the case of saturations parameterized by the pair so that the gain in the linear mode of the saturation is . Note that replaces intuitively the condition 1 + KG(jω0) = 0 of complex conjugate modes for the replacement . The precision of the computation of the locus , and then the precision of the calculated amplitude of the oscillation first-harmonic, depends on the type of describing function calculated for the saturation. See [36] and references therein for a number of useful describing functions/critical locus for different nonlinearities through different, but mutually close, useful definitions of describing function. The temporal asymptotic solution y(t) tends to the limit cycle of first-harmonic for any initial conditions;

(3) it is well known that electronic oscillators with basic saturated amplifiers of gain K (in their linear mode) require also linear network of at least third- order to be synthesized. See, for instance, [36]. This is because the impulse response hodograph G(jω) (being the Fourier transform, if it exists, of the impulse response of the dynamic system) of the linear feed-forward part of first- and second-order jointly stable and inversely stable systems (i.e., both poles and zeros are in Re  s < 0) are always in the third and fourth quadrants of the complex plane. As a result, they cannot cut the critical locus of a saturation nonlinearity for some frequency since such a critical locus is always allocated in the negative real semi axis;

(4) it is now described, in the context of the current problem at hand, how sustained oscillations can be obtained from the above described CADSC and SDADSC criteria by using just second-order systems of transfer functions G(s) = K(s + 1)/s2 in the feedforward loop. This implies that the order of the auxiliary linear network to synthesize the oscillator can be diminished related to the typical design using electronic circuitry whose basic amplifier in saturation mode needs the use of an auxiliary network of at least third-order. Then, consider again the feedback differential equation referred to above but under discrete control at, in general, nonperiodic sampling for CADSC and SDADSC:

()
where {ti} is the real sequence of sampling instants, and {Ti = ti+1 − ti}is the real sequence of sampling periods under the CADSC or the SDADSC sampling criteria for all  i ∈ N0 = N ∪ {0}. The above feedback system is a regulator since the control signal u(t) = e(t) = −y(ti)for all  t ∈ [ti,   ti+1) is generated by a zero-order hold under an identically zero external reference signal. If the control is identically zero then the resulting linear feedback is globally asymptotically Lyapunov stable to the origin which is the sole stable equilibrium point. However, the use of the sampling criteria translates into the presence of limit cycles that is, asymptotic oscillations being the limits of the solution trajectories in the phase plane. The following values are taken: K = 1, A = 0.2154 for the single threshold case as the sampling amplitude in the CADSC criterion and the set of amplitudes Samp ≡ {A1, A2, A3, A4} = {0.12,0.1677, 0.2154, 0.2631} for the SDADSC criterion injected in this order to implement the sampling criterion. Since the control is a regulator, r ≡ 0 for all time, then the sampling criterion becomes
()
for the CADSC, and
()
where [i/4] = Integer  Part(i/4); for all  i ∈ N0 = N ∪ {0} for the SDADSC. Note that the sampling criteria (5.6) and (5.7) can be interpreted as a separated nonlinearity of the dynamic systems (5.5) consisting of a multi-relay with hysteresis displayed in Figure 1 where m(ti) = −u(ti). In such a way, the sampling and hold device with the sampling criteria is equivalent to such a nonlinearity which could be potentially be generated in a completely different way by using relays with hysteresis. In the case of the SDADSC, the amplitudes are taken to vary consecutively in the defined order in the set of amplitudes of the sampling criterion. The asymptotic phase plot for the CADSC criterion and SDADSC criterion are, a limit cycle of fundamental amplitude and frequency 0.39 and 0.3079 cycles/sec., and another limit cycle of amplitude 0.31 and frequency 0.3095 cycles/sec., respectively. Both limit cycles to which the phase portraits of the trajectory solutions asymptotically converge are shown in Figure 2. A direct interpretation of why the asymptotic solution is a stable limit cyclic, so that the solution is bounded and the whole system is (nonasymptotically) stable relies on the equivalence of the tandem sampling criteria CADSC and SDADSC through a companion zero-order hold to two variants of the multiple hysteretic relay nonlinearity of Figure 1. Note that it is well known that nonlinear systems under certain conditions can generate limit cycles. The sequences of constant asymptotic sampling periods reached in both cases are also listed in the figure. Note that the fundamental amplitude of the second limit cycle corresponding to the SDADSC is reduced more that 20% with respect to the first one while the fundamental frequencies differ only in about 0.50%, the second one being very slightly larger than the first one. It has been also observed under exhaustive inspection of related examples by modifying their parameterizations that the duration of the transient time interval towards the limit cycle solution is slightly shorter under the first criterion compared to the second one.

If the sampling criterion is modified to the constant amplitude-based sampling criterion |y(t) + y(ti)| = Afor all  t ∈ [ti,   ti+1) (i.e., modified CADSC) and to the multithreshold sampling criterion obtained via its right-hand-side replacement by the same multithreshold sequence as above, that is, Samp ≡ {A1, A2, A3, A4} = {0.12,0.1677, 0.2154, 0.2631} (i.e., modified SDADSC) then one gets the results of Figure 3 below. Note the complex geometry of the asymptotic oscillations of the standard criteria displayed in Figure 2 compared to the more smooth shaped ones of the modified ones displayed in Figure 3. It can be pointed out that other potential sampling criteria, not been subject to constant or varying (within a prescribed set) differences of amplitude can lead to asymptotically stable solutions provided that the admissibility domain for the sampling intervals defined by such sampling criteria is constrained to the stability domain of a constant sampling provided that the continuous part of the dynamic system is globally asymptotically stable. See, for instance, Theorem 2.3.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Multirelay with hysteresis nonlinear characteristics of the sampling criterion.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Phase plane plot for the solution versus its first time derivative exhibiting closed limit trajectories.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Phase plane plot of the modified sampling criteria for the solution versus its first time derivative exhibiting limit cycles.

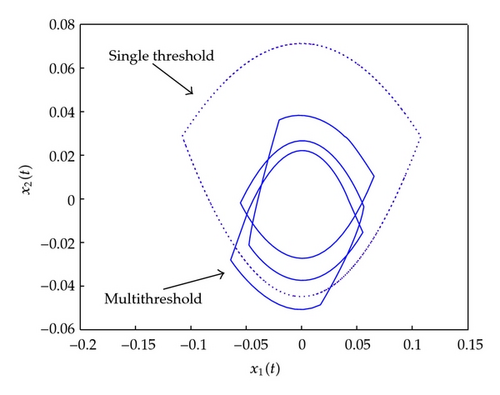
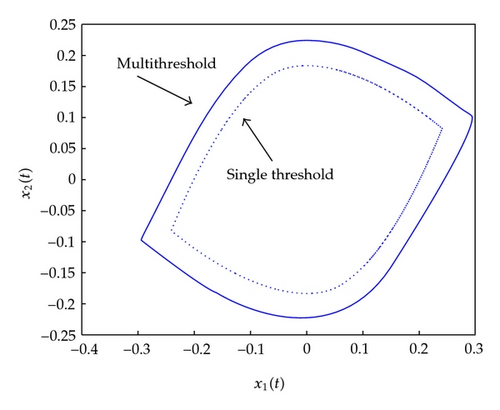
Remark 5.3. Note that Example 5.2 is based on a transfer function description of the linear part. Thus, the above mathematical results on the limit asymptotic solutions are applicable to any minimal state-space realization, since in this case the dimension of the linear system coincides with the order of the transfer function (i.e., its number of poles). In the case of nonminimal realizations (then being either noncontrollable or nonobservable or both), the above discussed results still hold if the cancelled modes are strictly stable since their contribution to the state-space trajectories and their timederivatives the relevant order vanish asymptotically as time tends to infinity.

6. Conclusions

This paper has been devoted to investigate the solutions and, in particular, their stability and instability properties as well as the possible presence of sustained oscillations in discrete linear dynamic systems under sampling laws which generate time-varying sampling periods in general. Two sampling criteria have been specially emphasized, namely, (a) the so-called constant amplitude difference sampling criterion (CADSC), under which the signal of interest is sampled at each time that it reaches a prescribed threshold variation which is the positive real constant defining the sampling criterion; (b) the more general sampling criterion is referred to as a sampling-dependent amplitude difference sampling criterion (SDADSC) which involves a set of at least two distinct of such amplitudes. Both sampling criteria possess the property that, together with their associate sampling and zero-order hold device, are characterized as a relay with multiple hysteresis. Such a nonlinear model is expected to potentially generate potentially sustained limit oscillations of the solution. The analysis has been fully performed in the time domain so that, contrarily to the case of the use of frequency-domain analysis methods, no specific assumption is needed about low-pass filtering constraints of the linear auxiliary network in order to perform the analysis of the first-harmonic of the existing sustained oscillations. It is noticed that, the proposed analysis, no separation of the first-order harmonic of the whole oscillation has to be taken in mind.

Acknowledgments

The authors thank the Spanish Ministry of Education and the Basque Government for their support of this work through Grants DPI2009-07197, IT378-10, and SAIOTEK S-PE09UN12. They also thank the editor of the special issue of “Modelling and Control of Complex Dynamic Systems: Applied Mathematics Aspects” and the anonymous referees and editor for their useful comments which helped the authors to improve the former versions of the paper.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.