Qualitative Analysis for a Predator Prey System with Holling Type III Functional Response and Prey Refuge
Abstract
A predator prey system with Holling III functional response and constant prey refuge is considered. By using the Dulac criterion, we discuss the global stability of the positive equilibrium of the system. By transforming the system to a Liénard system, the conditions for the existence of exactly one limit cycle for the system are given. Some numerical simulations are presented.
1. Introduction
Recently, the qualitative analysis of predator prey systems with Holling II or III types functional response and prey refuge has been done by several papers, see [1–5]. Their main objective is to discuss under what conditions the positive equilibrium of the corresponding system is stable or unstable and the existence of exactly one limit cycles. In general, the prey refuge has two types, one is the so-called constant proportion prey refuge: (1 − m)x, where m ∈ (0,1), the other type is called constant prey refuge: (x − m).
It easy to obtain the following lemma.
Lemma 1.1. Any solution (x(t), y(t)) of system (1.2) with initial condition x(0) > m, y(0) > 0 is positive and bounded for all t ≥ 0.
2. Basic Results
It is easy to obtain the following lemma.
Lemma 2.1. Let (H1) hold. Further assume that (H3) kα ≤ c and (H4) kα > c, m > max {0, (a − bx*)/b}. Then E0 is locally asymptotically stable, if any of (H3) and (H4) holds. When kα > c, 0 < m < (a − bx*)/b, E0 is unstable, furthermore, E0 is a saddle point.
About the properties of the positive equilibrium, we have the following theorem.
Theorem 2.2. Assume kα > c. Then
- (I)
E* is locally asymptotically stable for 0 < m < (a − bx*)/b if a(2c − kα) ≤ 2bcx* holds.
- (II)
E* is locally asymptotically stable for m1 < m < (a − bx*)/b and E* is locally unstable for 0 < m < m1 if a(2c − kα) > 2bcx* holds, where
(2.3) - (III)
system (2.1) undergoes Hopf bifurcation at m = m1 if a(2c − kα) > 2bcx* holds.
Proof. The Jacobian matrix of system (2.1) at E* is
Note that
- (I)
If a(2c − kα) ≤ 2bcx* holds, then m1 ≤ 0, R(m) < 0 holds for m1 < m < m2. Considering (H2) and m2 > (a − bx*)/b, for 0 < m < (a − bx*)/b, tr (J(E*)) < 0, which implies E* is locally asymptotically stable.
- (II)
If a(2c − kα) > 2bcx* holds, then m1 > 0, for m1 < m < m2, R(m) < 0, since , by , we obtain m1 < (a − bx*)/b. Together with (H2), for m1 < m < (a − bx*)/b, tr (J(E*)) < 0, which means E* is locally asymptotically stable. On the other hand, for 0 < m < m1, tr (J(E*)) > 0, E* is locally unstable.
- (III)
We have
(2.7)these satisfy Liu’s Hopf bifurcation criterion (see [6], page 255); hence, the Hopf bifurcation occurs at m = m1. This ends the proof.
3. Global Stability of the Positive Equilibrium
Denote .
Theorem 3.1. If E*(x*, y*) is locally stable. Further assume that max {0, (a − 4bβ)/2b} < m < m4, then the positive equilibrium E*(x*, y*) of system (2.1) is globally asymptotically stable.
Proof. Take the Dulac function B(x, y) = x−2y−1, for system (2.1) we have
If a = 2bm, ϕ(x) = 2b(x4 + m2β2) > 0 for x > 0.
On the other hand, there exist
Case 1. If a − 2bm > 0, then for 0 < x < x2, ϕ′′(x) < 0; for x > x2, ϕ′′(x) > 0. Hence, x = x2 is the least value of the function ϕ′(x). If β > x2, ϕ′(x2) = (a − 2bm)(β − x2)(β + x2) > 0, it has ϕ′(x) > 0 for all x > 0, then ϕ(x) is increasing for x > 0, notice that ϕ(0) > 0. Therefore, ϕ(x) > 0 for x > 0. Since, T < 0 for x > 0, system (2.1) does not exist limit cycle.
Case 2. If bm < a < 2bm, then x2 < 0, for x > 0, ϕ′′(x) > 0, hence, for x > 0, ϕ′(x) is increasing. Evidently, , then there exists such that ϕ′(x0) = 0, where , hence, when 0 < x < x0, ϕ′(x) < 0, when x > x0, ϕ′(x) > 0. We know that ϕ(x) takes the least value at x = x0, that is, ϕ(x) > ϕ(x0). According to ϕ′(x0) = 0, for x > 0 we obtain , where .
To prove ϕ(x) > 0 for x > 0, it suffices to prove for . Clearly, takes the least value at x = β, and is strictly decreasing at the interval (0, β). Hence, for holds. Since . Therefore, for holds if m3 < m < m4 holds, then for x > 0, ϕ(x) > 0 holds.
In sum, if one of the following three conditions holds (1) m = a/2b; (2) 0 < m < a/2b, x2 < β⇒max {0, (a − 4bβ)/2b} < m < a/2b; (3) a/2b < m < a/b, m3 < m < m4⇒a/2b < m < m4, the function T does not change the sign for x > 0, then system (2.1) does not exist limit cycle. It is easy to see that the conditions (1), (2), and (3) are equal to max {0, (a − 4bβ)/2b} < m < m4. The proof is completed.
4. Existence and Uniqueness of Limit Cycle
Theorem 4.1. If a(2c − kα) > 2bcx* holds, for 0 < m < m1 system (2.1) admits at least one limit cycle in Ω.
Proof. We construct a Bendixson loop which includes E* of system (2.1). Let be a length of the line L1: be a length of line L2:b(x + m) − a = 0. Define
Lemma 4.2 (see [7].)Let f(x), g(x) be continuously differentiable functions on the open interval (r1, r2), and φ(y) be continuously differentiable functions on R in
- (1)
dφ(y)/dy > 0,
- (2)
having a unique x0 ∈ (r1, r2), such that (x − x0)g(x − x0) > 0 for x ≠ x0 and g(x0) = 0,
- (3)
f(x0)d/dx(f(x)/g(x)) < 0 for x ≠ x0,
Theorem 4.3. If a(2c − kα) > 2bcx* holds, for system (2.1) exists exactly one limit cycle which is globally asymptotically stable in Ω.
Proof. Let u = x, v = ln y, τ = −x2t, still denote u, v, τ, as x, y, t, then system (2.1) becomes
Let , then transform to the origin O(0,0), still denote , as x, y yield
Clearly, F(0) = 0. It is easy to see that the conditions (1) and (2) of Lemma 4.2 for x0 = 0 are satisfied. Consider
Then, we have
By a simple computation, we obtain
Note that for 0 < m < a/b and . It follows from (4.6) that
Hence, there exists a point , such that , that is,
Together with (4.16), we obtain
Then all the conditions of Lemma 4.2 are satisfied, considering Theorem 4.1, we obtain the conclusion of this theorem. The proof is completed.
5. Numerical Simulations
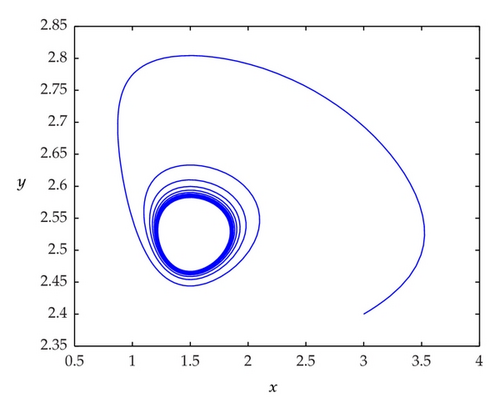
Take α = 0.5, k = 0.2, β = 0.5, a = 1, b = 0.1, and c = 0.09. Then a(2c − kα) − 2bcx* = 0.053, and m1 ≈ 1.986121812. One can see a Hopf bifurcation occurring at m = 1.955 and the bifurcated periodic solution is stable in Figure 1.
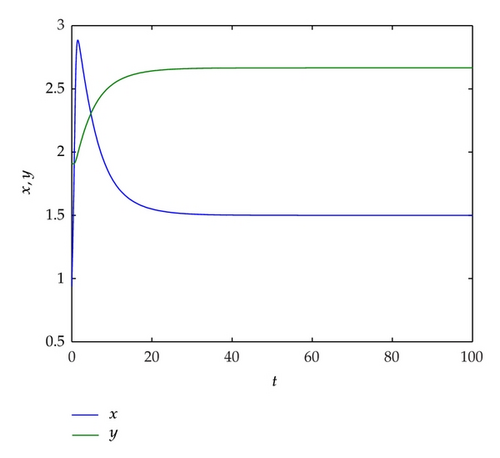
When taking m = 4.5, then x* = 1.5, y* ≈ 2.666666667, a(2c − kα) − 2bcx* = 0.053, m1 ≈ 1.986121812,(a − bx*)/b = 8.5, (a − 4bβ)/2b = 4, a/2b = 5. Theorem 3.1 is satisfied; the equilibrium E* of system (2.1) is globally asymptotically stable. See Figure 2.
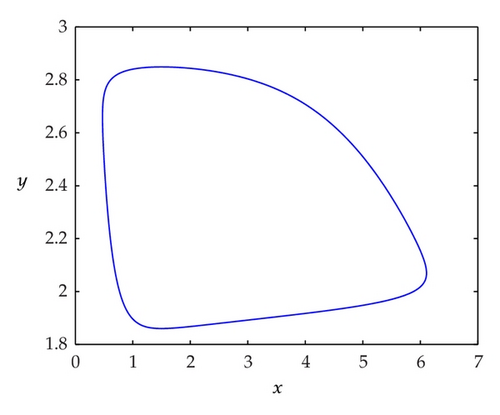
Take m = 1, we obtain E*(1.5,2.083333333), . The conditions in Theorem 4.1 are satisfied; hence, system (2.1) exists exactly one limit cycle which is globally asymptotically stable. One can see Figure 3.
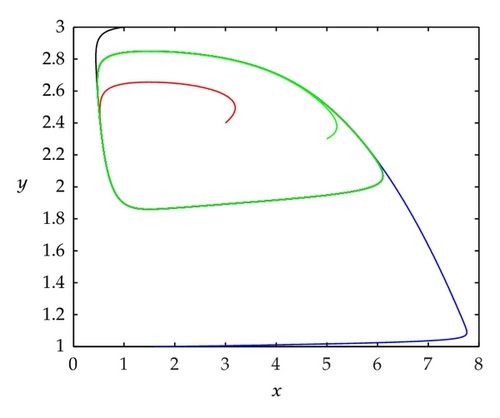
Acknowledgments
This work is partially supported by the National Natural Science Foundation of China (11226142), Foundation of Henan Educational Committee (2012A110012), Youth Science Foundation of Henan Normal University (2011QK04), Natural Science Foundation of Shanghai (no. 12ZR1421600), and Shanghai Municipal Educational Committee (no. 10YZ74).




