Journal of Applied Mathematics
Volume 2012, Issue 1 675287
Research Article
Open Access

Lie Group Analysis of Unsteady Flow and Heat Transfer over a Porous Surface for a Viscous Fluid

M. B. Akgül, 

M. B. Akgül

Department of Mechanical Engineering, Celal Bayar University, Muradiye, 45140 Manisa, Turkey

Search for more papers by this author
G. Sarı, 

G. Sarı

Applied Mathematics and Computation Center, Celal Bayar University, Muradiye, 45140 Manisa, Turkey

Search for more papers by this author
M. Pakdemirli, 

Corresponding Author

M. Pakdemirli

Applied Mathematics and Computation Center, Celal Bayar University, Muradiye, 45140 Manisa, Turkey

Search for more papers by this author
First published: 22 November 2012
https://doi.org/10.1155/2012/675287
Academic Editor: Fazal M. Mahomed

Abstract

The problem of a two-dimensional, unsteady flow and a heat transfer of a viscous fluid past a surface in the presence of variable suction/injection is analyzed. The unsteadiness is due to the time dependent free stream flow. The governing equations are derived with the usual boundary layer approximation. Using Lie group theory, a group classification of the equations with respect to the variable free stream flow and suction/injection velocity is performed. Restrictions imposed by the boundary conditions on the symmetries are discussed. Adopting the obtained symmetry groups, governing partial differential equations are converted into ordinary differential equations and then solved numerically. Effects of the dimensionless problem parameters on the velocity and temperature profiles are outlined in the figures.

1. Introduction

Boundary layer flow and heat transfer for an incompressible viscous fluid past a heated porous surface have attracted a great interest because of the importance in engineering applications such as cooling of nuclear reactors and turbine blades, food processing, crystal growth, flow control on airfoils, and electronic cooling. Blasius [1] first presented a similarity solution for velocity distribution within the boundary layer for a viscous incompressible fluid over a flat plate. Khaled and Vafai [2] studied hydromagnetic effects on dynamical and thermal boundary layer characteristics. This analysis is concerned with a family of squeezed flows. They displayed effects of the magnetic parameter, Prandtl number, suction/injection parameter, and squeezing parameter on velocity and temperature profiles graphically. Elbashbeshy and Bazid [3] studied the heat transfer over an unsteady stretching surface. They obtained a new similarity solution for the temperature field. They investigated the effect of the Prandtl number and the unsteadiness parameter which determine the velocity and temperature profiles and heat transfer coefficient. Mahmood et al. [4] studied flow and heat transfer over a permeable sensor surface placed in a squeezing channel. They displayed effects of the squeezing parameter on values of velocity and temperature and the variation of skin friction coefficient and heat transfer coefficient against the transpiration parameter with the graphics. Bataller [5] investigated the flow influenced by nonlinearly stretching of the sheet with heat transfer. They analyzed the effects of various physical parameters on heat transfer phenomena in a viscous flow over a nonlinearly stretching sheet. Mukhopadhyay [6] investigated the effects of thermal radiation on unsteady boundary layer mixed convection heat transfer problem from a vertical porous stretching surface embedded in a porous medium. Their study indicated that the flow and temperature field are significantly influenced by the unsteadiness parameter, buoyancy force, and suction parameter in both porous and nonporous media. Aziz [7] studied thermal boundary layer flow over a flat plate considering convective surface heat flux at the lower surface of the plate and determined the condition which the convection heat transfer coefficient must meet for a similarity solution to exist. Aziz [8] studied the boundary layer flow over a flat plate with slip flow and constant heat flux surface condition velocity and shear stress distributions were presented for a range of values of the parameter characterizing the slip flow. Ishak [9] considered the problem of steady laminar boundary layer flow and heat transfer over a stationary flat plate immersed in a uniform free stream with convective boundary condition. They found that suction increases the surface shear stress and as a consequence increases the heat transfer rate at the surface. Yao et al. [10] investigated heat transfer flow over a stretching/shrinking sheet with convective boundary conditions. They found that temperature at the surface of the plate increases with the increase of the surface convection parameter. Rahman [11] studied locally similar solutions for the hydromagnetic thermal boundary layer flow of a viscous incompressible electrically conducting fluid over a flat plate with a partial slip at the surface of boundary in the presence of the convective surface boundary condition numerically and displayed results for the velocity, temperature, and Prandtl number within the boundary layer delineating the effect of various parameters characterizing the flow.

In most of the published studies in the literature [12–16], the partial differential equations were converted to ordinary differential equations via a similarity transformation found by ad hoc methods. The resulting ordinary differential equations were then solved by numerical methods. Lie group methods are performed to investigate similarity transformation of the boundary layer equations in only a few studies [17–19]. However, a detailed investigation of the complete symmetries for unsteady boundary layer flow and heat transfer equations are lacking in the literature.

In this paper, Lie group analysis of unsteady flow and heat transfer over a porous surface in the presence of suction/injection velocity is analyzed. Group classification of the governing equations with respect to the variable free stream flow and suction/injection velocity is performed. The infinitesimal generators are obtained. The restrictions imposed by the boundary conditions on the generators are discussed. Using the resulting generators, the governing equations are transformed into ordinary differential equations and solved numerically. Numerical results are presented for the selected dimensionless problem parameters and discussed in detail. Present study reveals that injection decreases temperature gradient whereas suction increases the temperature gradient. The increase in the Prandtl number causes increase in the temperature gradient with increasing the slope.

2. Mathematical Formulation

Consider the unsteady two-dimensional, incompressible laminar flow over a porous surface. Under the boundary layer approximation, the continuity, momentum, and energy equations can be written as
(2.1)
where is the coordinate along the surface and is the coordinate vertical to . is time, and are the velocity components in and coordinates. is the free stream velocity outside the boundary layer, is the temperature, ν and α are the kinematic viscosity and thermal diffusivity of the fluid, respectively.
The boundary conditions are
(2.2)
where is the suction/injection velocity of the permeable surface. Ts is the constant surface temperature and T∞ is the temperature of the ambient fluid.
The nondimensional form of (2.1) and boundary conditions are as follows:
(2.3)
(2.4)
(2.5)
(2.6)
The nondimensional parameters are related to the dimensional ones through the following relations:
(2.7)
where U0, L, Re, and Pr are the average free stream velocity, length of the horizontal surface, Reynolds number, and Prandtl number, respectively. F(x, t) is used for simplicity in the equations.

3. Symmetry Analysis

The symmetry groups of (2.3)–(2.5) are calculated by using classical Lie group approach. Details of the theory can be found in Bluman and Kumei [20] and Stephani [21]. The one-parameter infinitesimals Lie group of transformations are defined as
(3.1)
The prolonged infinitesimal generator which includes higher order derivatives is
(3.2)
The invariance conditions for (2.3)–(2.5) are obtained by applying the generator to the equations:
(3.3)
MathLie program [22] is used to calculate higher order infinitesimals and then equations are separated with respect to higher order variables. The initial restrictions on the infinitesimals are
(3.4)
and the remaining determining equations are
(3.5)
Equations (3.5) are an overdetermined partial differential system. Solving the system, the infinitesimals are finally obtained:
(3.6)
F(x, t) is to be determined from the following equation:
(3.7)
The generator is applied to the boundary conditions which should also be invariant under the transformation leading to restrictions in (3.6):
(3.8)
or
(3.9)
V(x, t) and U(x, t) functions should satisfy the following equations:
(3.10)
Different functions can be obtained from (3.10) for V(x, t) and U(x, t) via setting the parameters as follows.
(I) Parameter a: selecting parameter a = 1 without a loss of generality and all other parameters zero yields
(3.11)
In this case, suction or injection velocity is an arbitrary function of time. Solving (3.11) for U(x, t) yields U = xf(t), where f(t) is an arbitrary function of time for this special choice.
(II) Parameter c: selecting parameter c = 1 and all other parameters zero yields
(3.12)
For this choice, V(x, t) and U(x, t) yield and U = (1/t)f(x) from (3.10).
(III) Parameter b: selecting parameter b = 1 and all other parameters zero yields
(3.13)
In this case, suction or injection velocity and free stream velocity are arbitrary functions of time.
(IV) Parameter e: selecting parameter e = 1 and all other parameters zero yields
(3.14)
In this case, suction or injection velocity and free stream velocity are arbitrary functions of the spatial variable x.

4. Similarity Transformations and Reductions

Similarity transformations and reductions of the partial differential system to an ordinary differential system will be considered.

4.1. A Similarity Transformation

In this section, we choose the first case (case I) for obtaining similarity transformations as follows:
(4.1)
Similarity variables and functions are obtained from (4.1):
(4.2)
The substitution of these variables and functions into the original equations and boundary conditions yields
(4.3)
(4.4)
The partial differential system with three independent variables is reduced to a system with two independent variables.

4.2. The Second Reduction

To reduce (4.3) and (4.4) into an ordinary differential system, one-parameter infinitesimal Lie group of transformations is defined as
(4.5)
The prolonged infinitesimal generator is
(4.6)
The invariance conditions for (4.3) are
(4.7)
(4.8)
(4.9)
Substituting the higher order infinitesimals, separating the equations with respect to higher order variables yields
(4.10)
from which the above equations are solved:
(4.11)
The determining equation for f(μ2) which is selected to U(x, t), outer velocity, is obtained as follows:
(4.12)
The boundaries and boundary conditions should be invariant under the transformations also (Bluman and Kumei [20]):
(4.13)
Two parameters are involved in Lie group Transformations.
s(μ2) and f(μ2) functions should satisfy the following equations:
(4.14)
Different functions can be obtained from the above equations for s(μ2) and f(μ2) via setting the parameters. The general case in which both parameters are involved will be considered.
Solving (4.14) results
(4.15)
The equations determining the similarity transformations are
(4.16)
from which the similarity variables and functions are derived:
(4.17)
Inserting these variables and functions into (4.3) and (4.4) yields the following ordinary differential system:
(4.18)
Further, we scale variables and β as
(4.19)
The substitution of these variables into (4.18) yields
(4.20)
The associated boundary conditions are
(4.21)
where λ1 is the suction/injection parameter; c1 and c3 are the unsteadiness parameters.

5. Result and Discussion

The nonlinear reduced ordinary differential equation system (4.20) with the boundary conditions in (4.21) is solved numerically by applying a finite difference code that implements the three-stage Lobatto IIIA formula that provides continuous solutions of fourth order accuracy in the problem domain. Description of the numerical method is given by Shampine et al. [23] and Kierzenka and Shampine [24]. Results are displayed graphically for various values of problem parameters to see developments in the velocity and temperature fields.

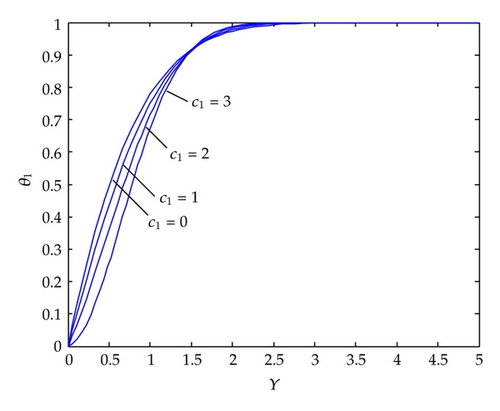
The variation of the dimensionless x-component of velocity is shown for various values of unsteadiness parameter c1 in the absence of suction/injection in Figure 1. It is clear that an increase in the c1 causes a reduction in the velocity until a certain point. After this point, reverse effect in velocity is observed for increasing values of c1.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Variation of θ1 for different values of unsteadiness parameter c1 (Pr = 10, λ1 = 0).

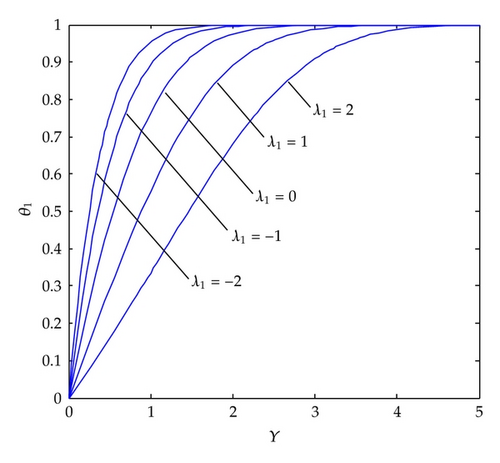
The effect of suction/injection parameter on the velocity profile is presented in Figure 2. It is noted that suction decreases the boundary layer thickness whereas injection increases.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Variation of θ1 for different values of suction/injection (Pr = 10, c1 = 0.5).

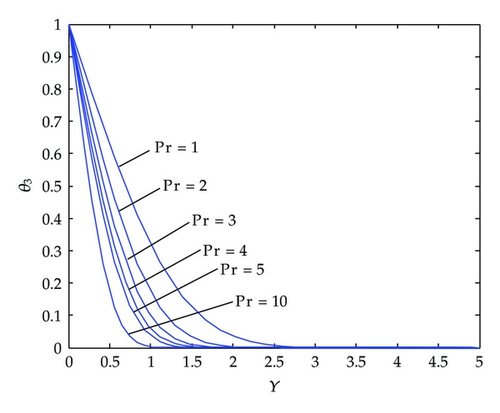
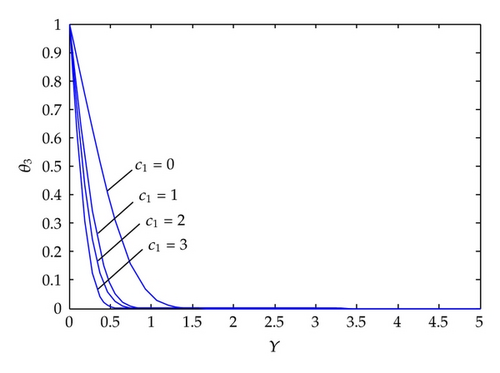
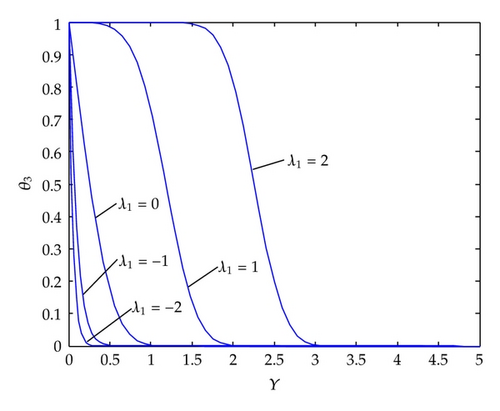
Effects of Prandtl number on the temperature profiles are given in Figure 3. An increase in the Prandtl number decreases the temperature profiles. Effects of unsteadiness parameter c1 on the temperature profiles are depicted in Figure 4. An increase in c1 decreases the temperature profiles. Thermal boundary layer is narrower for higher unsteadiness parameter. In Figure 5 effects of suction-injection parameter on the temperature profiles are depicted. λ1 = 0 corresponds to no suction/injection case. Suction decreases the thickness of thermal boundary layer whereas injection increases the thickness of thermal boundary layer.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Variation of θ3 for different values of the Prandtl number (λ1 = 0, c1 = 0.5).
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Variation of θ3 for different values of c1 (Pr = 10, λ1 = 0).
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Variation of θ3 for different values of suction/injection (Pr = 10, c1 = 0.5).

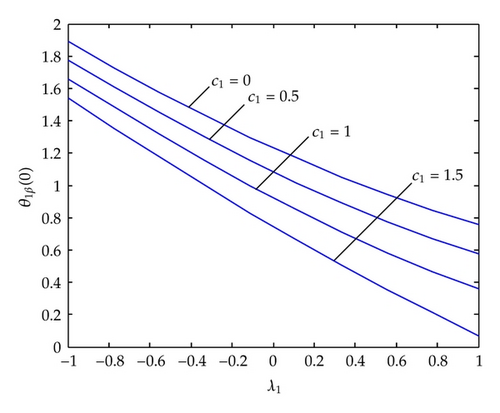
In Figure 6, we displayed the velocity gradient against suction/injection parameter for the case of flow along a horizontal porous surface for different values of the unsteadiness parameter, c1. Injection decreases the velocity gradient whereas suction increases the velocity gradient. The reduction in c1 causes an increase in velocity gradient with decreasing the slope.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Variation of the velocity gradient with c1 (Pr = 1).

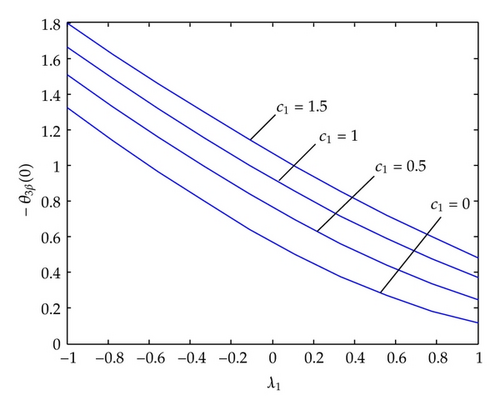
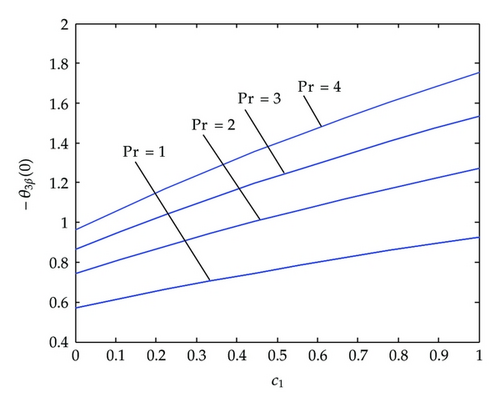
In Figure 7, we show the temperature gradient against suction/injection parameter for different c1-unsteadiness parameter. Injection decreases the temperature gradient whereas suction increases the temperature gradient. In Figure 8, we displayed the temperature gradient against unsteadiness parameter for different Prandtl numbers. The increase in the Prandtl number causes increase in temperature gradient.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Variation of the temperature gradient with λ1 (Pr = 1).
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Variation of the temperature gradient with c1 (λ1 = 0).

6. Conclusions

In this paper, we have studied the problem of two-dimensional, unsteady flow and heat transfer of a viscous fluid past a surface in the presence of variable suction/injection. The unsteadiness is due to time dependent free stream flow.

The governing equations are derived with the usual boundary layer approximation. Using Lie group theory, a group classification of the equations with respect to the variable free stream flow and suction/injection velocity is performed. Restrictions imposed by the boundary conditions on the symmetries are discussed. Adopting the obtained symmetry groups, governing partial differential equations are converted into ordinary differential equations and then solved numerically.

Effects of dimensionless problem parameters on the velocity and temperature profiles are outlined in the figures. From the present investigation the following results are obtained.
  • (i)

    An increase in the unsteadiness parameter c1 causes a reduction in the velocity.

  • (ii)

    Suction decreases the boundary layer thickness whereas injection increases.

  • (iii)

    An increase in the Prandtl number and unsteadiness parameter decreases the temperature profiles.

  • (iv)

    Suction decreases the thickness of thermal boundary layer whereas injection increases the thickness of boundary layer.

  • (v)

    Injection decreases the velocity gradient whereas suction increases. Moreover the reduction of c1 causes an increase in the velocity gradient.

  • (vi)

    Injection decreases the temperature gradient whereas suction increases the temperature gradient. The increase in the Prandtl number causes increase in the temperature gradient with increasing the slope.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.