Volume 2012, Issue 1 645214

Research Article

Open Access

Existence and Global Stability of a Periodic Solution for Discrete-Time Cellular Neural Networks

Haijian Shao,

Corresponding Author

Haijian Shao

[email protected]

Department of Automation, Southeast University, Nanjing, Jiangsu 210096, China seu.ac.bd

Search for more papers by this author

Haikun Wei,

Haikun Wei

Department of Automation, Southeast University, Nanjing, Jiangsu 210096, China seu.ac.bd

Search for more papers by this author

Haoxiang Wang,

Haoxiang Wang

Department of Automation, Southeast University, Nanjing, Jiangsu 210096, China seu.ac.bd

Search for more papers by this author

Haijian Shao,

Corresponding Author

Haijian Shao

[email protected]

Department of Automation, Southeast University, Nanjing, Jiangsu 210096, China seu.ac.bd

Search for more papers by this author

Haikun Wei,

Haikun Wei

Department of Automation, Southeast University, Nanjing, Jiangsu 210096, China seu.ac.bd

Search for more papers by this author

Haoxiang Wang,

Haoxiang Wang

Department of Automation, Southeast University, Nanjing, Jiangsu 210096, China seu.ac.bd

Search for more papers by this author

First published: 10 December 2012

https://doi.org/10.1155/2012/645214

Citations: 1

Academic Editor: Kwok-Wo Wong

Share a link

Email
Wechat
Bluesky

Abstract

A novel sufficient condition is developed to obtain the discrete-time analogues of cellular neural network (CNN) with periodic coefficients in the three-dimensional space. Existence and global stability of a periodic solution for the discrete-time cellular neural network (DT-CNN) are analysed by utilizing continuation theorem of coincidence degree theory and Lyapunov stability theory, respectively. In addition, an illustrative numerical example is presented to verify the effectiveness of the proposed results.

1. Introduction

Cellular neural networks (CNNs) are the basis of both discrete-time cellular neural networks (DT-CNNs) [1] and the cellular neural networks universal machine (CNNs-UM). The dynamical behaviour of Chua and Yang cellular neural network (CY-CNN) is given by the state equation

(1.1)

where I, u, y, and x denotes input bias, input, output, and state variable of each cell, respectively. N_r(ij) is the t-neighbourhood of cell C(k, l) as N_r(ij) = {C(k, l)∣max {|k − i|, |l − j|} ≤ r}, i and j denote the position of the cell in the network, k and l denote the position of the neighbour cell relative to the cell in consideration. B is the nonlinear weights template matrices for input feedback and A is the corresponding template matrices for the outputs of neighbour cells. Non-linearity means that templates can change over time.

A large number of cellular neural networks (CNNs) models have appeared in the literature [2–4], and these models differ in cell complexity, parameterization, cell dynamics, and network topology. Various generalizations of cellular neural networks have attracted attention of scientific community due to their promising potential for tasks of classification, associative memory, parallel computation [5–9], pattern recognition, computer vision, and solving any optimization problem [10–13]. Such applications rely on the existence of equilibrium points and the qualitative properties of cellular neural networks.

Discrete-time cellular neural networks (DT-CNNs) have been studied both in theory and applications. Previous results introduced many properties of DT-CNN in the two dimensional plane. For instance, [14] has been successfully applied to investigate the discrete-time analogues of cellular neural network (CNN) with variable coefficients in the two-dimensional plane. However, three-dimensional structure is more accurate, specific, and closer to real structures of CNN. Based on the above discussion, this paper proposes some effective results of DT-CNN in the three-dimensional space.

Motivated by the constructing of continuous system (1.1), the discrete analogue of the system (1.1) is considered as follows:

(1.2)

For any h > 0, the discrete-time analogues (1.2) converge to the continuous-time system (1.1) will be provided. Without loss of generality, (1.2) can be substituted in the DT-CNNs model:

(1.3)

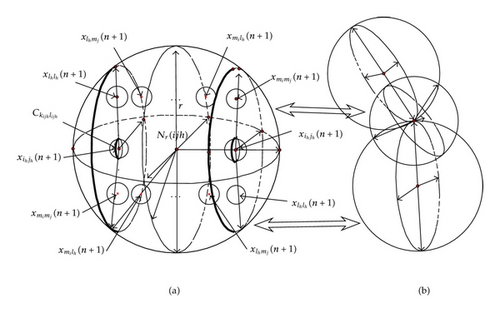
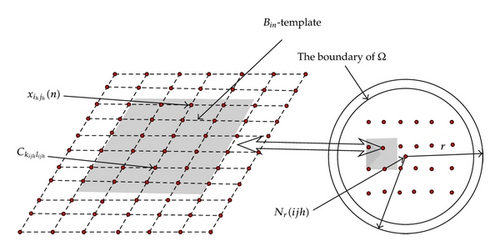
Then, the spatial structure with respect to (1.3) is shown in Figure 1, where , Ω≜{x ∈ 𝒳 ⊂ N_r(ijh), ∥x∥ < Θ}, N_r(ijh) is the r-neighbourhood of a cell , and Θ will be denoted by the proof of Theorem 3.1 in Section 3.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Spatial structure with respect to (1.3).

The rest of the paper is organized as follows: in Section 2, system description and preliminaries are developed in detail and some definitions, assumptions, and lemmas are stated. Section 3 gives sufficient conditions for a periodic solution for DT-CNN in three-dimensional space by utilizing continuation theorem of coincidence degree theory. Section 4 proposes global stability of a periodic solution for the DT-CNN. A numerical simulation is given to show correctness of our analysis in Section 5 and concluded in Section 6.

2. System Preliminaries and Description

Consider the following model which is equivalent to the (1.3):

(2.1)

where α(h) = e^−h, β(h) = 1 − α(h), for all h > 0, φ_ij(n) are N(h)-periodic sequences, that is, φ_ij(n) = φ_ij(n + N(h)).

Throughout the paper, the following definitions and lemmas will be introduced.

Definition 2.1 (Fredholm operator). Let 𝒳 and 𝒴 be a Banach space, an operator L is called Fredholm operator if L is a bounded linear operator between 𝒳 and 𝒴 whose kernel and cokernel are finite-dimensional and whose range is closed. Equivalently, an operator L : 𝒳 → 𝒴 is Fredholm if it is invertible modulo compact operator, that is, if there exists a bounded linear operator S : 𝒴 → 𝒳 such that Id_𝒳 − SL, Id_𝒴 − LS are compact operators on 𝒳 and 𝒴, respectively, where Id_𝒳 and Id_𝒴 are the identity operator.

Definition 2.2 (L-compact). An operator N will be called L-compact on if the open bounded set is bounded and is compact, where K_p is the inverse operator of N. Since Im Q is isomorphic to Ker L, there exists an isomorphism J : Im Q → Ker L.

The index of a Fredholm operator is ind L = dim Ker L–codim Im L, then operator L will be called a Fredholm operator of index zero if dim Ker L = codim Im L < +∞ and Im L is closed in 𝒴. Then a following abstract equation in Banach space 𝒳 is defined by

(2.2)

Let L : Dom L ⊂ 𝒳 → 𝒴 be linear operator, and N : 𝒳 → 𝒴 be a continuous operator. If L is a Fredholm operator of index zero, there must exist continuous projectors P : 𝒳 → 𝒳 and Q : 𝒴 → 𝒴, such that:

(2.3)

In other words, L|_{Dom L∩Ker P} : Dom L∩Ker P → Im L is invertible, and the inverse of the operator L is denoted by K_p.

Lemma 2.3 (Gaines and Mawhin [15]). Let 𝒳 be a Banach space, L be a Fredholm operator of index zero, and let be L-compact on , where Ω is an open bounded set, suppose:

(2.4)

Then Lx = Nx has at least one solution in

Lemma 2.4. If a and b are some certain nonnegative vectors, then there exists a positive constant β, such that ab ≤ (β/2)a² + (1/2β)b².

Proof. Assuming a and b are some certain non-negative vectors, β is a positive constant, then

(2.5)

Thus, the proof of Lemma 2.4 is completed.

Assumption 2.5. ) are N-periodic sequence of . For the sake of convenience, we use the following notations: . For each operator P : N_r(ijh) → N_r(ijh) and any s = s(u, v, w), t = t(i, j, h) ∈ N_r(ijh), such that:

(2.6)

where o_ijh is the spherical centre of N_r(ijh) with a radius length r, m_ijh = max {|m_i|, |m_j|, |m_h|}, then it is easy to obtain: |P(s) − P(t)| ≤ ∥P∥|(s − t)| ≤ 2m_ijhr < + ∞.

Assumption 2.6. There is a positive constant , such that , for all x₁ ≠ x₂ ∈ R.

3. Existence of a Periodic Solution with respect to (2.1)

In many cases, many proposed results are not ideal and therefore it is necessary to formulate a novel and effective result for DT-CNN in the three-dimensional space. Can we obtain the result about the existence and stability of a periodic solution for DT-CNN in three-dimensional space? This is the topic we wish to address in this paper. The aim of the present work is to develop a strategy to determine the existence and global stability of a periodic solution with respect to (2.1) in the three-dimensional space. Consequently, we processed with the following result.

Theorem 3.1. Suppose that Assumptions 2.5 and 2.6 hold, and the following condition holds:

(3.1)

where

, i = 1, …, m_i, j = 1, …, m_j, n ∈ I_N = {0, 1, …, N − 1}, then (2.1) has at least one N-periodic solution.

Proof. In this section, by means of using Mawhin’s continuation theorem of coincidence degree theory, we will study the existence of at least one periodic solution with respect to (2.1), for convenience, some following notations will be used:

(3.2)

where f(n) is any function. Let

, and y^N ⊂ 𝒳 = 𝒴 be the subspace of all N-periodic sequence; equip it with the norm

. For any ε > 0,

, there exists N(ε) > 0 and ε > 0, such that

. Thus,

is a Cauchy sequence in N_r(ijh) and o_ijh is the spherical centre of N_r(ijh), d(x, y) = max {|x − y| : x ∈ X}. By utilizing the meaning of N_r(ijh) and Bolzano-Weierstrass theorem (Each bounded sequence in Rⁿ has a convergent subsequence, here

), it is easy to know that (𝒳, ∥·∥) is a Banach space.

Set

(3.3)

that is

(3.4)

where

, for all n ∈ I_N. Then we will learn that dim Ker L = codim Im L < +∞, it is easy to prove that L is a bounded linear operator, P and Q are two continuous operators such that Ker L = Im P, Im L = Ker Q = Im (I − Q), and

, that is

(3.5)

that is

(3.6)

where δ(β(h), n, N) is a constant, which is only depended on variables h, n, and N.

Obviously, employing the Lebesgue’s convergence theorem, we can easily learn that is bounded, is compact for any open bounded set Ω ⊂ 𝒳⊂N_r(ijh) by using Ascoli-Arzela’s theorem (A subset ℱ of 𝒞(𝒳) is compact if and only if it is closed, bounded and equi-continuous). Thus, N is L-compact on a closed set with any open bounded set Ω ⊂ 𝒳 ⊂ N_r(ijh).

Suppose that is a solution with respect to (2.1), for certain λ ∈ (0,1). Then the following equation can be derived by (2.2):

(3.7)

Then, the following results can be derived by utilizing (3.7):

(3.8)

where

. Therefore, the solution with respect to (2.1) is bounded for certain λ ∈ (0,1). In other words,

(3.9)

Then the open bounded set Ω is presented as follows:

(3.10)

Thus Lx ≠ λNx for any (x, λ)∈(∂Ω∩Dom L)×(0,1), the Ω satisfies condition (i) in Lemma 2.3.

In Figure 2, the nonlinear weights template matrices B and the boundary of Ω are shown, respectively. Then for any two dimensional plane of any spherical neighbourhood is denoted. Thus, for any , , it is easy to learn that x is a constant vector in with ∥x∥ = Θ; Thus, we have

(3.11)

where

. Furthermore, we can calculate the bound of QNx as follows:

(3.12)

where

, i = 1, …, m_i, j = 1, …, m_j, n ∈ I_N. Thus for any x = ∂Ω∩Ker L, QNx ≠ 0, this proves the condition (ii) in Lemma 2.3.

In order to prove the condition (iii) is satisfied with respect to (2.1), we only need to prove that deg (JQN, Ω∩Ker L, 0) ≠ 0. Define Φ : Dom L → 𝒳 by

(3.13)

where

, for all n ∈ I_N.

Now we will prove that , ≠ (0,0,…,0)^T. If this is not true, then , , thus, for constant vector x ∈ ∂Ω, we have:

(3.14)

Equivalently, (3.14) can be written as the following form:

(3.15)

Combining (3.12) and (3.15), the following results are obtained:

(3.16)

Thus, the following result is derived by calculating the (3.16):

(3.17)

Obviously, (3.17) is a contradiction since ((1 + β(h))/β(h)) > 1, then for any x = ∂Ω∩Ker L, Ker L = Im P, , . Thus, deg (JQN, Ω ∩ Ker L, 0) ≠ 0. Therefore, (2.1) has at least one N-periodic solution, thus the proof of Theorem 3.1 is completed.

Corollary 3.2. Suppose that Assumptions 2.5 and 2.6 hold, and the following condition holds:

(3.18)

where

, i = 1, …, m_i, j = 1, …, m_j, n ∈ I_N, then (2.1) has at least one N-periodic solution.

Proof. Similar to the proof of Theorem 3.1, so it is omitted.

4. Globally Stability of a Periodic Solution with respect to (2.1)

The existence of a periodic solution for the system (2.1) is derived in the Theorem 3.1. Then global stability of a periodic solution with respect to (2.1) in the three-dimensional space is presented in the following.

Theorem 4.1. Suppose that Assumptions 2.5 and 2.6 hold, and the following condition holds:

(4.1)

where i = 1, 2, …, m_i,

,m_j and m_h are positive constants, then the periodic solution with respect to (2.1) is global stability.

Proof. It follows from the Theorem 3.1 that (2.1) has at least a periodic solution, without loss of generality, the periodic solution can be described by:

(4.2)

Then we can define the following formula:

(4.3)

Now, we show that the a periodic solution x^*[n] is globally stable, and the following inequality is obtained by utilizing (2.1) and (4.3):

(4.4)

We design the following Lyapunov-type sequence V[n] by

(4.5)

Then, we can calculate the ΔV[n] by combining (2.1) and (4.5):

(4.6)

Thus, it is easy to obtain V[n] ≤ V[0] by the meaning of the (4.6), and furthermore,

(4.7)

where

Obviously, from the proof of Theorem 4.1, the globally stable of a periodic solution with respect to (2.1) is derived. Then, existence and global stability of a periodic solution for DT-CNNs are obtained by utilizing the conditions of the proposed theorems in an arbitrary diameter plane of a convex space. Thus the proof of Theorem 4.1 is completed.

5. Numerical Simulation

In this section, we give an example to show the effectiveness and improvement of the derived results. Consider the following continuous cellular neural networks:

(5.1)

for t > 0, where

. Then, state trajectories of x_ij(i = 1, 2, 3, j = 1, 2) are denoted in Figure 3.

From Figure 3, it is easy to know that a (1/4)-periodic solution of the continuous cellular neural networks is globally stable. Compared to the system (5.1), we design the discrete-time analogue of the continuous cellular neural network as follows:

(5.2)

for h > 0, by using Assumptions 2.5 and 2.6 in Section 2, each variable is denoted as:

(5.3)

The derived results of this paper are verified by the following steps.

(1) According to the illustrations of the neighbourhood distance r for cell

which is given by N_r(ijh) function, and by (3.9) and (3.10), the exact values of distance r and Ω are illustrated as:

(5.4)

Then, Θ_ij(i = 1,2, 3, j = 1,2) is calculated below,

(5.5)

Thus, the subset Ω of function N_r(ijh) is derived by the following:

(5.6)

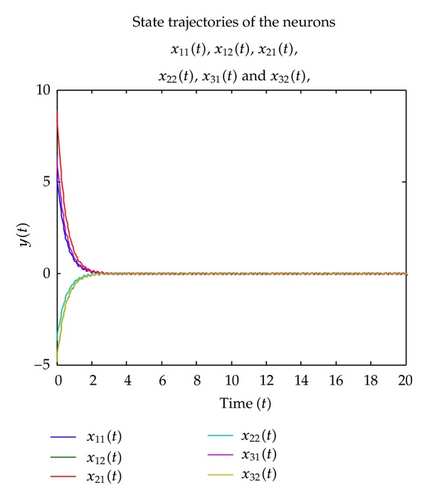
(2) We will verify the condition of Theorem 3.1 if we want to utilize Theorem 4.1. After strictly calculating the condition of Theorem 3.1, it is easy to obtain that the function , i = 1,2, 3, j = 1, 2, n ∈ I_N; therefore, the condition of the Theorem 3.1 is critically satisfied as well.

(3) According to (4.1), the condition of the Theorem 4.1 will be derived as follows:

(5.7)

Then state trajectories of neurons x₁₁, x₁₂, x₂₁, x₂₂, x₃₁, x₃₂ are shown in Figures 4 and 5.

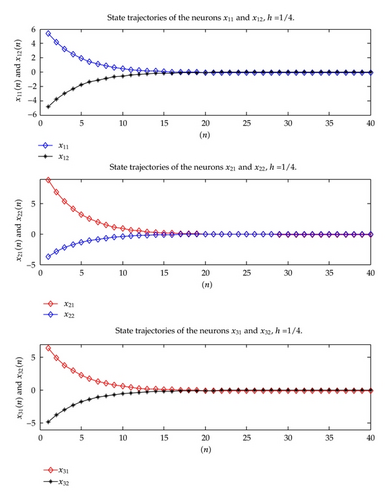
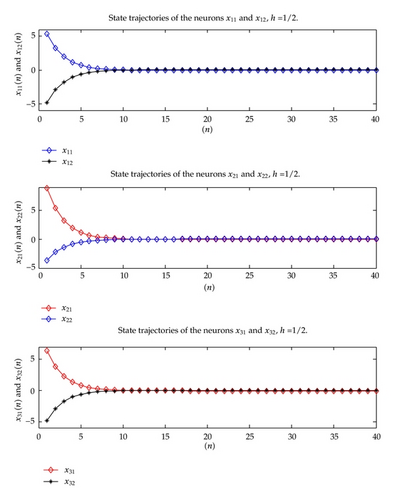
From Figures 4 and 5, we can learn that all the periodic solution converges to a unique a 1/4h-periodic solution, then the DT-CNN (2.1) has a globally stable 1/4h-periodic solution. Thus, all conditions of Theorems 3.1 and 4.1 are strictly satisfied; therefore all conditions of proposed theorems are critically verified.

6. Conclusions

Existence and global stability are important dynamical properties in CNN. In this paper, we consider the discrete-time analogues of CNN with periodic coefficients and obtain some new results for the DT-CNN in the three-dimensional space. Comparisons between our results and the previous results have also been made. And it has been demonstrated that our criteria are more general and effective than those reported in the literature.

Acknowledgments

The authors wish to acknowledge Major Program of National Natural Science Foundation (NNSF) of China under Grants 11190015 and 60875035, Research Fund for the Doctoral Program of Higher Education of China under Grant 20100092110020, and Scientific Research Foundation of Graduate School of Southeast University under Grant YBJJ1215.

References

1 Chua L. O. and Yang L., Cellular neural networks: theory, IEEE Transactions on Circuits and Systems. (1988) 35, no. 10, 1257–1272, https://doi.org/10.1109/31.7600, 960777, ZBL0663.94022.
10.1109/31.7600
Web of Science® Google Scholar
2 Zhang Q., Yang L., and Liao D., Existence and exponential stability of a periodic solution for fuzzy cellular neural networks with time-varying delays, International Journal of Applied Mathematics and Computer Science. (2011) 21, no. 4, 649–658, https://doi.org/10.2478/v10006-011-0051-9, 2919967.
10.2478/v10006-011-0051-9
Web of Science® Google Scholar
3 Akhmet M. U., Aruğaslan D., and Yılmaz E., Stability in cellular neural networks with a piecewise constant argument, Journal of Computational and Applied Mathematics. (2010) 233, no. 9, 2365–2373, https://doi.org/10.1016/j.cam.2009.10.021, 2577773, ZBL1191.68484.
10.1016/j.cam.2009.10.021
Web of Science® Google Scholar
4 Stamova I., Akca H., and Stamov G., Qualitative analysis of dynamic activity patterns in neural networks, Journal of Applied Mathematics. (2011) 2011, 2, 208517.
10.1155/2011/208517
Google Scholar
5 Javier Martinez J., Javier Toledo F., and Manuel Ferrandez J., Discrete-time cellular neural networks in FPGA, Proceedings of the International Symposium on Field-Programmable Custom Computing Machines, 2007, 293–294.
Google Scholar
6 Balasubramaniam P., Samath J. A., Kumaresan N., and Kumar A. V. A., Solution of matrix Riccati differential equation for the linear quadratic singular system using neural networks, Applied Mathematics and Computation. (2006) 182, no. 2, 1832–1839, https://doi.org/10.1016/j.amc.2006.06.020, 2282625, ZBL1107.65057.
10.1016/j.amc.2006.06.020
Web of Science® Google Scholar
7 Balasubramaniam P., Abdul Samath J., and Kumaresan N., Optimal control for nonlinear singular systems with quadratic performance using neural networks, Applied Mathematics and Computation. (2007) 187, no. 2, 1535–1543, https://doi.org/10.1016/j.amc.2006.09.072, 2321358, ZBL1114.65336.
10.1016/j.amc.2006.09.072
Web of Science® Google Scholar
8 Mali K. and Mitra S., Symbolic classification, clustering and fuzzy radial basis function network, Fuzzy Sets and Systems. (2005) 152, no. 3, 553–564, https://doi.org/10.1016/j.fss.2004.10.001, 2140489, ZBL1101.68775.
10.1016/j.fss.2004.10.001
Web of Science® Google Scholar
9 Barmpalexis P., Kanaze F. I., Kachrimanis K., and Georgarakis E., Artificial neural networks in the optimization of a nimodipine controlled release tablet formulation, European Journal of Pharmaceutics and Biopharmaceutics. (2010) 74, 316–323.
10.1016/j.ejpb.2009.09.011
CAS PubMed Web of Science® Google Scholar
10 Zhang J., Global stability analysis in delayed cellular neural networks, Computers & Mathematics with Applications. (2003) 45, no. 10-11, 1707–1720, https://doi.org/10.1016/S0898-1221(03)00149-4, 1993240, ZBL1045.37057.
10.1016/S0898-1221(03)00149-4
Web of Science® Google Scholar
11 Zhang W. and Wang L., Robust stochastic stability analysis for uncertain neutral-type delayed neural networks driven by Wiener process, Journal of Applied Mathematics. (2012) 2012, 12, 829594, https://doi.org/10.1155/2012/829594, 2852853, ZBL1235.93196.
10.1155/2012/829594
Google Scholar
12 Javier Martinez J., Javier Toledo F., and Manuel Ferrandez J., Implementation of a discrete cellular neuron model (DT-CNN) architecture on FPGA, Bioengineered and Bioinspired Systems II. (2005) 5839, 332–340.
10.1117/12.608118
Google Scholar
13 Zhang Y., Asymptotic stability of impulsive reaction-diffusion cellular neural networks with time-varying delays, Journal of Applied Mathematics. (2012) 2012, 17, 501891, https://doi.org/10.1155/2012/501891, 2854974, ZBL1235.93197.
10.1155/2012/501891
Google Scholar
14 Li Y., Global stability and existence of periodic solutions of discrete delayed cellular neural networks, Physics Letters A. (2004) 333, no. 1-2, 51–61, https://doi.org/10.1016/j.physleta.2004.10.022, 2101961, ZBL1123.39302.
10.1016/j.physleta.2004.10.022
CAS Web of Science® Google Scholar
15 Gaines D. R. E. and Mawhin J. L., Coincidence Degree and Non-Linear Differential Equations, 1977, Springer, Berlin, Germany.
10.1007/BFb0089537
Google Scholar

Citing Literature

All articles

Existence and Global Stability of a Periodic Solution for Discrete-Time Cellular Neural Networks

Abstract

1. Introduction

2. System Preliminaries and Description

3. Existence of a Periodic Solution with respect to (2.1)

4. Globally Stability of a Periodic Solution with respect to (2.1)

5. Numerical Simulation

6. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Existence and Global Stability of a Periodic Solution for Discrete-Time Cellular Neural Networks

Abstract

1. Introduction

2. System Preliminaries and Description

3. Existence of a Periodic Solution with respect to (2.1)

4. Globally Stability of a Periodic Solution with respect to (2.1)

5. Numerical Simulation

6. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information