A class of Cohen-Grossberg-type BAM neural networks with distributed delays and impulses are investigated in this paper. Sufficient conditions to guarantee the uniqueness and global exponential stability of the periodic solutions of such networks are established by using suitable Lyapunov function, the properties of M-matrix, and some suitable mathematical transformation. The results in this paper improve the earlier publications.

1. Introduction

The research of neural networks with delays involves not only the dynamic analysis of equilibrium point but also that of periodic oscillatory solution. The dynamic behavior of periodic oscillatory solution is very important in learning theory due to the fact that learning usually requires repetition [1, 2].

Cohen and Grossberg proposed the Cohen-Grossberg neural networks (CGNNs) in 1983 [3]. Kosko proposed bi directional associative memory neural networks (BAMNNs) in 1988 [4]. Some important results for periodic solutions of delayed CGNNs have been obtained in [5–10]. Xiang and Cao proposed a class of Cohen-Grossberg BAM neural networks (CGBAMNNs) with distributed delays in 2007 [11]; in addition, many evolutionary processes are characterized by abrupt changes at certain time; these changes are called to be impulsive phenomena, which are included in many neural networks such as Hopfield neural networks, BAM neural networks, CGNNs, and CGBAMNNs and can affect dynamical behaviors of the systems just as time delays. The results for periodic solutions of CGBAMNNs with or without impulses are obtained in [11–15].

The objective of this paper is to study the existence and global exponential stability of periodic solutions of CGBAMNNs with distributed delays by using suitable Lyapunov function, the properties of M-matrix, and some suitable mathematical transformation. Comparing with the results in [13, 14], improved results are successively obtained, the conditions for the existence and globally exponential stability of the periodic solution of such system without impulses have nothing to do with inputs of the neurons and amplification functions; and we also point that CGBAMNNs model is a special case of CGNNs model, many results of CGBAMNNs can be directly obtained from the results of CGNNs.

The rest of this paper is organized as follows. Preliminaries are given in Section 2. Sufficient conditions which guarantee the uniqueness and global exponential stability of periodic solutions for CGBAMNNs with distributed delays and impulses are given in Section 3. Two examples are given in Section 4 to demonstrate the main results.

2. Preliminaries

Consider the following periodic CGNNs model with distributed delays and impulses:

(2.1)

where 1 ≤ i ≤ n, t > 0, and Z⁺ = {1,2, …}. x_i(t) denotes the state variable of the ith neuron, f_j(·) denotes the signal function of the jth neuron at time t; I_i denotes input of the ith neuron at time t; a_i(·) represents amplification function; b_i(t, ·) is appropriately behaved function; p_ij(t) and u_ij(t) are connection weights of the neural networks at time t; respectively, ρ_j is positive constant, which corresponds to the neuronal gain associated with the neuronal activations and k_ij corresponds to the delay kernel function; p_ij(t) and u_ij(t) are continuously periodic functions on [0, +∞) with common period T > 0.

; t_k is called impulsive moment and satisfies 0 < t₁ < t₂ < ⋯, lim_k→+∞t_k = +∞; x_i(t⁻) and x_i(t⁺) denote the left-hand and right-hand limits at t_k; respectively, we always assume and .

For system (2.1), we assume the following.

(H₁)
The amplification function a_i(·) is continuous, and there exist constants such that for 1 ≤ i ≤ n.
(H₂)
The behaved function b_i(t, ·) is T-periodic about the first argument; there exists continuous T-periodic function α_i(t) such that

(2.2)

for all x ≠ y, 1 ≤ j ≤ n.

(H₃)
For activation function f_j(·), there exists positive constant L_j such that

(2.3)

for all x ≠ y, 1 ≤ j ≤ n.
(H₄)
The kernel function k_ij(s) is nonnegative continuous function on [0, +∞) and satisfies

(2.4)

is differentiable function for λ ∈ [0, r_ij), 0 < r_ij < +∞, K_ij(0) = 1 and
(H₅)
There exists positive integer k₀ such that and hold.

Remark 2.1. A typical example of kernel function is given by for s ∈ [0, +∞), where r_ij ∈ (0, +∞), r ∈ {0,1, …, n}. These kernel functions are called as the gamma memory filter [16] and satisfy condition (H₄).

For any continuous function S(t) on [0, T], and denote min _t∈[0,T] {|S(t)|} and max _t∈[0,T] {|S(t)|}, respectively.

For any , t > 0, define , and for any , s ∈ (−∞, 0], define

Denote

(2.5)

Then PC((−∞, 0], R^k) is a Banach space with respect to ∥·∥.

The initial conditions of system (2.1) are given by

(2.6)

where φ(s) = (φ₁(s), φ₂(s), …, φ_n(s)) ∈ PC([−∞, 0], Rⁿ).

Let x(t, φ) = (x₁(t, φ), x₂(t, φ), …, x_n(t,φ)^T) denote any solution of the system (2.1) with initial value φ ∈ PC((−∞, 0], Rⁿ).

Definition 2.2. A solution x(t, φ) of system (2.1) is said to be globally exponentially stable, if there exist two constants λ > 0, M > 0 such that

(2.7)

for any solutions x(t, ψ) of system (2.1).

Definition 2.3. A real matrix is said to be a nonsingular M-matrix if a_ij ≤ 0 (i, j = 1,2, …, n, i ≠ j), and all successive principle minors of A are positive.

Lemma 2.4 (see [17].)A matrix with nonpositive off-diagonal elements is a nonsingular M-matrix if and if only there exists a vector such that p^TA > 0 or Ap holds.

Lemma 2.5. Under assumptions (H₁)–(H₅), system (2.1) has a T-periodic solution which is globally exponentially stable, if the following conditions hold.

(H₆)
ℳ = A − C is a nonsingular M-matrix, where

(2.8)

(H₇)
a_i((1 − γ_ik)s) ≥ |1 − γ_ik|a_i(s), for all s ∈ R, i = 1,2, …, n.

Proof. Let x(t, ψ₁) and x(t, ψ₂) be two solutions of system (2.1) with initial value ψ₁ = (φ₁, φ₂, …, φ_n) and ψ₂ = (ζ₁, ζ₂, …, ζ_n) ∈ PC((−∞, 0], Rⁿ), respectively.

Let

(2.9)

Since ℳ is a nonsingular M-matrix according to condition (H₆), ℳ^T is also a nonsingular M-matrix; we know from Lemma 2.4 that there exists a vector

such that ℳ^Tp > 0; that is,

(2.10)

for 1 ≤ i ≤ n, which indicates that F_i(0) > 0. Since F_i(θ) are continuous and differential on [0, r_ji) and

according to condition (H₄),

for θ ∈ [0, u_ji). There exist constants θ_i such that F_i(θ_i) = 0 for i = 1,2, …, n. So we can choose

(2.11)

such that

(2.12)

Define

(2.13)

Now we define a Lyapunov function V(t) by

(2.14)

in which

(2.15)

for i = 1,2, …, n.

When t ≠ t_k, k ∈ Z⁺, calculating the upper right derivative of V(t) along solution of (2.1), similar to proof of Theorem 3.1 in [10], corresponding to case in which r → 1, v_ijl(t) = 0 in [10], we obtain from (2.12)–(2.15) that

(2.16)

When t = t_k, k ∈ Z⁺, we have

(2.17)

which, together with (H₇), leads to

(2.18)

that is,

(2.19)

It follows that

(2.20)

Then we have

(2.21)

On the other hand, from (2.14), we have

(2.22)

in which

(2.23)

Hence, from (2.21) and (2.22), we know that the following inequality holds for t > 0:

(2.24)

in which M = M₀/m₀.

We can always choose a positive integer N such that and define a Poincaré mapping P : C → C by P(ξ) = x_T(ξ); we have

(2.25)

which implies that P^N is a contraction mapping. Similar to [10], using contraction mapping principle, we know that system (2.1) has a T-periodic solution which is globally exponentially stable. This completes the proof.

Remark 2.6. The result above also holds for (2.1) without impulses, and the existence and globally exponential stability of the periodic solution for (2.1) have nothing to do with amplification functions and inputs of the neuron. The results in [5] have more restrictions than Lemma 2.5 in this paper because conditions for the ones in [5] are relevant to amplification functions.

3. Periodic Solutions of CGBAMNNs with Distributed Delays and Impulses

Consider the following periodic CGBAMNNs model with distributed delays:

(3.1)

for 1 ≤ i ≤ n, 1 ≤ j ≤ m, and Z⁺ = {1,2, …}; x_i(t) and y_j(t) denote the state variable of the ith neuron from the neural field F_X and the jth neuron from the neural field F_Y at time t; f_j(·) and g_i(·) denote the signal functions of the jth neuron from the neural field F_Y and the ith neuron from the neural field F_X at time t; respectively, I_i and J_j denote inputs of the ith neuron from the neural field F_X and the jth neuron from the neural field F_Y at time t; respectively, a_i(·) and c_j(·) represent amplification functions; b_i(t, ·) and d_j(t, ·) are appropriately behaved functions; p_ij(t), q_ji(t), u_ij(t), and v_ji(t) are the connection weights;

are positive constants, which correspond to the neuronal gains associated with the neuronal activations; k_ij and

correspond to the delay kernel functions; u_ij(t), v_ji(t), p_ij(t), q_ji(t), I_i(t), and J_j(t) are all continuously periodic functions on [0, +∞) with common period T > 0.

, ; t_k is called impulsive moment and satisfies 0 < t₁ < t₂ < ⋯, lim _k→+∞ t_k = +∞; x_i(t⁻), y_j(t⁻) and x_i(t⁺), y_j(t⁺) denote the left-hand and right-hand limits at t_k; respectively, we always assume , and .

For system (3.1), we assume the following.

(H₈)
Amplification functions a_i(·) and c_j(·) are continuous and there exist constants and such that .
(H₉)
b_i(t, u), d_j(t, u) are T-periodic about the first argument, there exist continuous, T-periodic functions α_i(t) and β_j(t) such that
(3.2)
for all x ≠ y, 1 ≤ i ≤ n, 1 ≤ j ≤ m.

(H₁₀)
For activation functions f_j(·) and g_i(·), there exist constant L_j and such that
(3.3)
(H₁₁)
The kernel functions k_ij(s) and are nonnegative continuous functions on [0, +∞) and satisfy
(3.4)
are differentiable functions for λ ∈ [0, r_ij) and ; respectively, , , and
(H₁₂)
There exists positive integer k₀ such that and hold.

We assume that system (3.1) has the following initial conditions:

(3.5)

where ψ = (φ, ϕ) ∈ PC((−∞, 0], R^n+m), φ(s) = (φ₁(s), φ₂(s), …, φ_n(s)), ϕ(s) = (ϕ₁(s), ϕ₂(s), …, ϕ_m(s)).

Let Z(t, ψ) = (x(t, ψ), y(t, ψ)) denote any solution of the system (3.1) with initial value ψ = (φ, ϕ) ∈ PC, x(t, ψ) = (x₁(t, ψ), x₂(t, ψ), …, x(t_n, ψ)), y(t, ψ) = (y₁(t, ψ), y₂(t, ψ), …, y_m(t, ψ)).

Theorem 3.1. Under assumptions (H₈)–(H₁₂), there exists a T-periodic solution which is asymptotically stable, if the following conditions hold.

(H₁₃)
The following ℳ is a nonsingular M-matrix, and
(3.6)
in which
(3.7)
(H₁₄)
a_i((1 − γ_ik)s)≥|1 − γ_ik | a_i(s), c_j((1 − δ_jk)s)≥|1 − δ_jk | c_j(s), ∀ s ∈ R, i = 1,2, …, n, j = 1,2, …, m.

Proof. Let

(3.8)

It follows that system (3.1) can be rewritten as

(3.9)

for 1 ≤ i ≤ n, 1 ≤ j ≤ m.

Initial conditions are given by

(3.10)

Thus system (3.9) is a special case of system (2.1) in mathematical form, under conditions (H₈)–(H₁₄), we obtain from Lemma 2.5 that system (3.9) has a T-periodic solution which is globally exponentially stable if a_i((1 − γ_ik)s) ≥ |1 − γ_ik|a_i(s) and the following matrix ℳ′ is a M-matrix, and

(3.11)

where

(3.12)

in which

Then, we know from (3.8) and (3.11) that Theorem 3.1 holds.

If a_i(x_i(t)) = c_j(y_j(t)) = 1, b_i(t, x_i(t)) = b_i(t)x_i(t) and d_j(t, y_j(t)) = d_j(t)y_j(t), where b_i(t) and d_j(t) are positive continuous T-periodic functions for i = 1,2, …, n, j = 1,2, …, m. System (3.1) reduces to the following Hopfield-type BAM neural networks model:

(3.13)

Corollary 3.2. Under assumptions (H₉)–(H₁₂), there exists a T-periodic solution which is globally asymptotically stable, if the following conditions hold.

The following ℳ is a nonsingular M-matrix, and
(3.14)
in which
(3.15)
0 ≤ γ_ik ≤ 2, 0 ≤ δ_jk ≤ 2 for i = 1,2, …, n, j = 1,2, …, m, k ∈ Z⁺.

Proof. As b_i(t, x_i(t)) = b_i(t)x_i(t) and d_j(t, y_j(t)) = d_j(t)y_j(t), we obtain α_i(t) = b_i(t) and β_j(t) = d_j(t) in (), () implies () holds. Since a_i(x_i(t)) = c_j(y_j(t)) ≡ 1, then condition () reduces to (). Corollary 3.2 Holds from Theorem 3.1.

Remark 3.3. The conditions for the existence and globally exponential stability of the periodic solution of (3.1) without impulses have nothing to do with inputs of the neuron and amplification functions. The results in [13, 14] have more restrictions than Theorem 3.1 in this paper because conditions for the ones in [13, 14] are relevant to amplification functions and inputs of neurons our results should be better. In addition, Corollary 3.2 is similar to Theorem 2.1 in [15]; our results generalize the results in [15].

Remark 3.4. In view of proof of Theorem 3.1, since CGBAMNNs model is a special case of CGNNs model in form as BAM neural networks model is a special case of Hopfield neural networks model, many results of CGBAMNNs can be directly obtained from the ones of CGNNs, needing no repetitive discussions. Since system (3.1) reduces to autonomous system, Theorem 3.1 still holds, which means that system (3.1) has a equilibrium which is globally asymptotically stable; we know that many results in [18] can be directly obtained from the results in [19].

4. Two Simple Examples

Example 4.1. Consider the following CGNNs model with distributed delays:

(4.1)

Obviously, system (4.1) satisfies

–(

Note that

(4.2)

it is a nonsingular M-matrix and system (4.1) also satisfies condition (H₆). According to Lemma 2.5, system (4.1) has a 2π-periodic solution which is globally exponentially stable. Figure 1 shows the dynamic behaviors of system (4.1) with initial condition (0.1,0.2).

However, It is easy to check that system (4.1) does not satisfy Theorem 4.3 or 4.4 in [5], so theorems in [5] cannot are used to ascertain the existence and stability of periodic solutions of system (4.1).

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Time response of state variables x₁, x₂ and phase plot in space (t, x₁, x₂) for system (4.1).

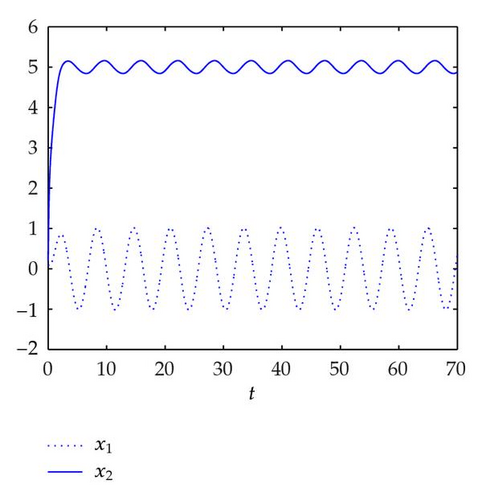
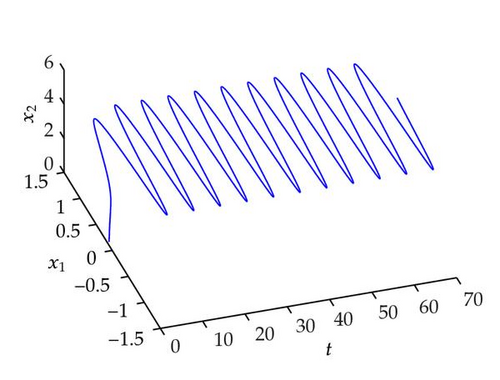
Example 4.2. Consider the following CGBAMNNs model with distributed delays and impulses:

(4.3)

where t_k = πk, k ∈ Z⁺.

Obviously, system (4.3) satisfies (H₈)–(H₁₂).

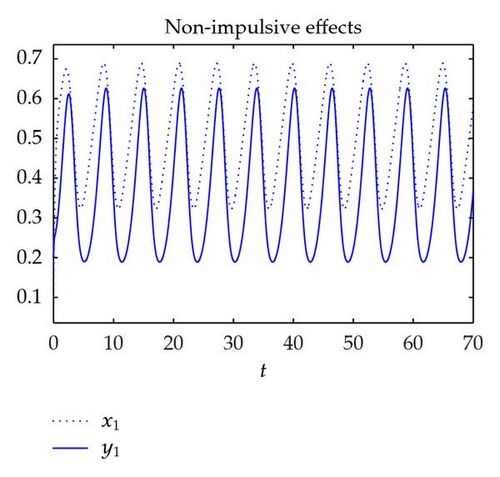
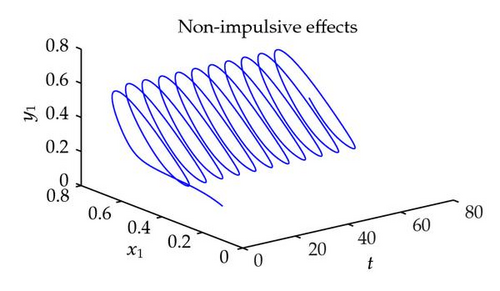
Case 1. γ_1k = 0, δ_1k = 0. Note that

(4.4)

it is a nonsingular M-matrix and system (4.3) also satisfies condition (H₁₃). According to Theorem 3.1, system (4.3) without impulses has a 2π-periodic solution which is globally exponentially stable. Figure 2 shows the dynamic behaviors of system (4.3) with initial condition (0.1,0.2).

However, it is easy to check that system (4.3) without impulses does not satisfy Theorem 1 in [13] and theorems in [14]; so theorems in [13, 14] cannot be used to ascertain the existence and stability of periodic solutions of system (4.3).

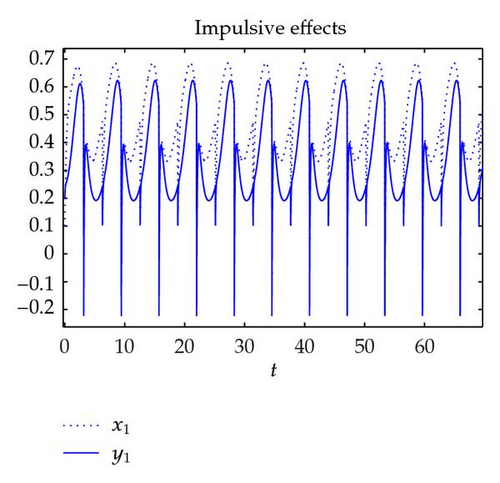
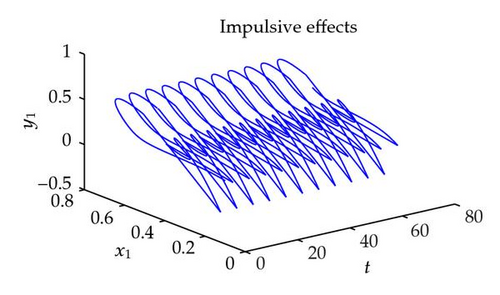
Case 2. γ_1k = 0.7, δ_1k = (1 − 0.5sin (t_k + 1)). Note that a₁(s) = 2 + sin s, c₁(s) = 3 + cos s, and and , which means condition (H₁₄) also holds for system (4.3). Hence, system (4.3) with impulses still has that there exists a 2π-periodic solution which is globally asymptotically stable. Figure 3 shows the dynamic behaviors of system (4.3) with initial condition (0.1,0.2).

This example illustrates the feasibility and effectiveness of the main results obtained in this paper, and it also shows that the conditions for the existence and globally exponential stability of the periodic solutions of CGBAMNNs without impulses have nothing to do with inputs of the neurons and amplification functions. If impulsive perturbations exist, the periodic solutions still exist and they are globally exponentially stable when we give some restrictions on impulsive perturbations.

5. Conclusions

A class of CGBAMNNs with distributed delays and impulses are investigated by using suitable Lyapunov functional, the properties of M-matrix, and some suitable mathematical transformation in this paper. Sufficient conditions to guarantee the uniqueness and global exponential stability of the periodic solutions of such networks are established without assuming the boundedness of the activation functions. Lemma 2.5 improves the results in [5], and Theorem 3.1 improves the results in [13, 14] and generalize the results in [15]. In addition, we point that CGBAMNNs model is a special case of CGNNs model; many results of CGBAMNNs can be directly obtained from the ones of CGNNs, needing no repetitive discussions. Our results are new, and two examples have been provided to demonstrate the effectiveness of our results.

Acknowledgment

The authors would like to thank the editor and the reviewers for their valuable suggestions and comments which greatly improved the original paper. Projects supported by the National Natural Science Foundation of China (no. 11071254).

Appendix

The source program (MATLAB 7.0) of Figure 1 is given as follows [14].

clear
T=70;
N=7000;
h=T/N;
m=40/h;
for i=1:m
U(:,i)=[0.1; 0.2];
end
for i=(m+1):(N+m)
r(i)=i*h-40;
x(i)=r(i);
I=2;
J=2+cos(U(2,i-1));
A=[-I,0; 0,-J];
B=[0,sin(x(i))*I; 0.3*J,0];
U(:,i)=h*A*[(U(1,i-1)-0.2*tanh(U(1,i-1))); U(2,i-1)]+U(:,i-1);
P(:,1)=[0; 0];
for k=1:m
P(:,1)=P(:,1)+h*exp(-(40-(k-1)*h))*[(tanh(U(1,i-m+k-1)));(tanh(U(2,i-m+k-1)))];
end
U(:,i)=U(:,i)+B*h*[(P(1,1));(P(2,1))]+h*[0; 5*J];
end
y=U(1,:);
z=U(2,:);
hold on
plot(r,y,’:’)
hold on
plot(r,z)
hold on
plot3(r,y,z)

The source program (MATLAB 7.0) of Figures 2 and 3 is given as follows [14].

clear
T=70;
N=7000;
h=T/N;
m=40/h;
for i=1:m
U(:,i)=[0.1;0.2];
end
for i=(m+1):(N+m)
r(i)=i*h-40;
x(i)=r(i);
I=2+sin(U(1,i-1));
J=3+cos(U(2,i-1));
A=[-I,0;0,-J];
B=[0,I*sin(x(i)); J*sin(x(i)),0];
U(:,i)=h*A*[2*U(1,i-1);(3+cos(x(i)))*U(2,i-1)]+U(:,i-1);
P(:,1)=[0;0];
for k=1:m
P(:,1)=P(:,1)+h*exp(-(40-(k-1)*h))*[(abs(U(1,i-m+k-1)));(abs(U(2,i-m+k-1)))];
end
U(:,i)=U(:,i)+B*h*[(P(1,1));(P(2,1))]+[I; J]*h;
if mod(i-m,314)==0
U(:,i)=[0.3,0; 0,1/2*(sin(x(i)+1))]*U(:,i);
end
end
y=U(1,:);
z=U(2,:)
hold on
plot(r,y,’:’)
hold on
plot(r,z)
hold on
plot3(r,y,z)

References

1 Huang Z. and Xia Y., Exponential periodic attractor of impulsive BAM networks with finite distributed delays, Chaos, Solitons and Fractals. (2009) 39, no. 1, 373–384, 2504572, https://doi.org/10.1016/j.chaos.2007.04.014, ZBL1197.34124.
10.1016/j.chaos.2007.04.014
Web of Science® Google Scholar
2 Townley S., Ilchmann A., Weiß M. G., Mcclements W., Ruiz A. C., Owens D. H., and Prätzel-Wolters D., Existence and learning of oscillations in recurrent neural networks, IEEE Transactions on Neural Networks. (2000) 11, no. 1, 205–214, https://doi.org/10.1109/72.822523.
10.1109/72.822523
CAS PubMed Web of Science® Google Scholar
3 Cohen M. A. and Grossberg S., Absolute stability of global pattern formation and parallel memory storage by competitive neural networks, IEEE Transactions on Systems, Man, and Cybernetics. (1983) 13, no. 5, 815–826, 730500, ZBL0553.92009.
10.1109/TSMC.1983.6313075
Web of Science® Google Scholar
4 Kosko B., Bidirectional associative memories, IEEE Transactions on Systems, Man, and Cybernetics. (1988) 18, no. 1, 49–60, https://doi.org/10.1109/21.87054, 931862.
10.1109/21.87054
Web of Science® Google Scholar
5 Sun J. and Wan L., Global exponential stability and periodic solutions of Cohen-Grossberg neural networks with continuously distributed delays, Physica D. (2005) 208, no. 1-2, 1–20, 2167905, https://doi.org/10.1016/j.physd.2005.05.009, ZBL1086.34061.
10.1016/j.physd.2005.05.009
Web of Science® Google Scholar
6 Li Y., Existence and stability of periodic solutions for Cohen-Grossberg neural networks with multiple delays, Chaos, Solitons and Fractals. (2004) 20, no. 3, 459–466, 2024869, https://doi.org/10.1016/S0960%2D0779(03)00406%2D5, ZBL1048.34118.
10.1016/S0960-0779(03)00406-5
Web of Science® Google Scholar
7 Li C.-H. and Yang S.-Y., Existence and attractivity of periodic solutions to non-autonomous Cohen-Grossberg neural networks with time delays, Chaos, Solitons and Fractals. (2009) 41, no. 3, 1235–1244, 2537636, https://doi.org/10.1016/j.chaos.2008.05.005, ZBL1198.34139.
10.1016/j.chaos.2008.05.005
Web of Science® Google Scholar
8 Song Q., Cao J., and Zhao Z., Periodic solutions and its exponential stability of reaction-diffusion recurrent neural networks with continuously distributed delays, Nonlinear Analysis. Real World Applications. (2006) 7, no. 1, 65–80, https://doi.org/10.1016/j.nonrwa.2005.01.004, 2183798, ZBL1094.35128.
10.1016/j.nonrwa.2005.01.004
Web of Science® Google Scholar
9 Yang X., [email protected], Existence and global exponential stability of periodic solution for Cohen-Grossberg shunting inhibitory cellular neural networks with delays and impulses, Neurocomputing. (2009) 72, no. 10-12, 2219–2226, https://doi.org/10.1016/j.neucom.2009.01.003.
10.1016/j.neucom.2009.01.003
Web of Science® Google Scholar
10 Liu Q. and Xu R., Periodic solutions of high-order Cohen-Grossberg neural networks with distributed delays, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 7, 2887–2893, 2772303, https://doi.org/10.1016/j.cnsns.2010.10.002, ZBL1221.37215.
10.1016/j.cnsns.2010.10.002
Web of Science® Google Scholar
11 Xiang H. and [email protected], Cao J., [email protected], Exponential stability of periodic solution to Cohen-Grossberg-type BAM networks with time-varying delays, Neurocomputing. (2009) 72, no. 7-9, 1702–1711, https://doi.org/10.1016/j.neucom.2008.07.006.
10.1016/j.neucom.2008.07.006
Web of Science® Google Scholar
12 Li Y., [email protected], Chen X., and Zhao L., Stability and existence of periodic solutions to delayed Cohen-Grossberg BAM neural networks with impulses on time scales, Neurocomputing. (2009) 72, no. 7–9, 1621–1630, https://doi.org/10.1016/j.neucom.2008.08.010.
10.1016/j.neucom.2008.08.010
Web of Science® Google Scholar
13 Chen A. and Cao J., Periodic bi-directional Cohen-Grossberg neural networks with distributed delays, Nonlinear Analysis. Theory, Methods & Applications. (2007) 66, no. 12, 2947–2961, https://doi.org/10.1016/j.na.2006.04.016, 2311648, ZBL1122.34055.
10.1016/j.na.2006.04.016
Web of Science® Google Scholar
14 Li X., Existence and global exponential stability of periodic solution for impulsive Cohen-Grossberg-type BAM neural networks with continuously distributed delays, Applied Mathematics and Computation. (2009) 215, no. 1, 292–307, 2568331, https://doi.org/10.1016/j.amc.2009.05.005, ZBL1190.34093.
10.1016/j.amc.2009.05.005
PubMed Web of Science® Google Scholar
15 Li Y.-t. and Wang J., An analysis on the global exponential stability and the existence of periodic solutions for non-autonomous hybrid BAM neural networks with distributed delays and impulses, Computers & Mathematics with Applications. (2008) 56, no. 9, 2256–2267, 2466746, https://doi.org/10.1016/j.camwa.2008.03.048, ZBL1165.34410.
10.1016/j.camwa.2008.03.048
Web of Science® Google Scholar
16 Principle J., Kuo J., and Celebi S., An analysis of the gamma memory in dynamics neural networks, IEEE Transactions on Neural Networks. (1994) 5, 337–361.
Google Scholar
17 Varga R. S., Matrix Iterative Analysis, 2000, 27, Springer, Berlin, Germany, 1753713.
10.1007/978-3-642-05156-2
Google Scholar
18 Li K., Zhang L., Zhang X., and Li Z., Stability in impulsive Cohen-Grossberg-type BAM neural networks with distributed delays, Applied Mathematics and Computation. (2010) 215, no. 11, 3970–3984, 2578862, https://doi.org/10.1016/j.amc.2009.12.001, ZBL1191.34091.
10.1016/j.amc.2009.12.001
Web of Science® Google Scholar
19 Li K., Stability analysis for impulsive Cohen-Grossberg neural networks with time-varying delays and distributed delays, Nonlinear Analysis. Real World Applications. (2009) 10, no. 5, 2784–2798, https://doi.org/10.1016/j.nonrwa.2008.08.005, 2523241, ZBL1162.92002.
10.1016/j.nonrwa.2008.08.005
Web of Science® Google Scholar

Citing Literature

All articles

Periodic Solutions of a Cohen-Grossberg-Type BAM Neural Networks with Distributed Delays and Impulses

Abstract

1. Introduction

2. Preliminaries

3. Periodic Solutions of CGBAMNNs with Distributed Delays and Impulses

4. Two Simple Examples

5. Conclusions

Acknowledgment

Appendix

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Periodic Solutions of a Cohen-Grossberg-Type BAM Neural Networks with Distributed Delays and Impulses

Abstract

1. Introduction

2. Preliminaries

3. Periodic Solutions of CGBAMNNs with Distributed Delays and Impulses

4. Two Simple Examples

5. Conclusions

Acknowledgment

Appendix

References

Citing Literature

Figures

References

Related

Information